饱和黏性土中重质非水相有机污染物纵向迁移数值模拟

高彦斌，张松波，李 韬，沈 超

（1.同济大学土木工程学院，上海200092；2.中建三局集团有限公司工程总承包公司，湖北武汉430064；3.湖北中建三局建筑工程技术有限责任公司，湖北武汉430070；4.上海勘察设计研究院（集团）有限公司，上海200093）

非水相有机污染物（NAPL）是地下环境污染防治焦点之一，其按照密度分为两种：比水重的称为重质非水相有机污染物（DNAPL），比水轻的称为轻非水相有机污染物（LNAPL）。从20世纪60年代开始，国内外对NAPL类水土污染问题开展了大量研究工作，尤其是DNAPL在重力作用下的竖向迁移。目前大部分研究工作集中在DNAPL在砂质含水层中的与重力作用有关的纵向迁移、与地下水径流有关的横向迁移以及黏土质隔水层顶部自由相DNAPL池的形成［1-4］，在迁移特征和迁移机理方面积累了丰富的研究成果，普遍认为DNAPL-水两相流以及对流弥散作用是控制DNAPL在砂质含水层中迁移的主要因素。

那么，到达渗透率较低的饱和黏性土隔水顶板处的DNAPL是否会再继续向下侵入到较深的位置，是一个需要探讨的问题。Essaid等［5］在对NAPL的迁移和归趋的研究综述中指出，在20世纪80年代以前，人们普遍认为所有黏土或淤泥沉积物都可以有效防止地下水被污染，但随着对一些地区污染场地的调查，发现承压含水层也会有这类污染物的存在。我国沿海地区地表十几米深度范围内广泛分布着饱和黏性土（包括粉质黏土和黏土两大类），旧农药厂和化工厂排放了大量的DNAPL污染物。上海地区旧农药厂区多次发现DNAPL在这类场地中迁移到十余米深度的案例。余梅［6］也曾报道了武汉市某化工厂的氯苯类有机物在饱和黏性土地层中迁移至较深位置。国外有学者认为黏土层中的裂隙（fractures）或孔洞是DNAPL进入土层的优先选择通道［7］；也有学者认为由于饱和黏性土中的地下水流速较低，分子扩散作用是DNAPL在饱和黏性土中迁移的主要方式［8］。总体上讲，目前国内外对饱和黏性土场地的DNAPL迁移规律和机理的认识还非常有限。

由于渗透性低，饱和黏性土中DNAPL的迁移会表现出与砂土含水层中不同的特征：①地下水流速小（几乎静止），因而与流速有关的对流弥散作用会大大消弱；②土中孔隙较小，DNAPL难以大量侵入，造成了室内试验研究的一些困难，如难以获得DNAPL的准确含量；③土的渗透性小，迁移速度慢，室内试验周期长。这些客观因素制约了相关试验研究的进展，也是导致目前国内外对饱和黏性土场地的DNAPL迁移规律和机理的认识非常有限的一个重要原因。本文采用数值分析法进行这方面的研究，讨论DNAPL-水两相流以及对流弥散作用这两种物理作用对饱和黏性土场地中DNAPL纵向迁移的影响，揭示其主要规律及机理。

1 饱和土中DNAPL迁移控制方程

1.1 DNAPL的存在状态及转化过程

DNAPL在饱和黏土中的存在状态有3种：水中溶解相、吸附于土颗粒的固态以及可流动的自由相。图1给出了这3种状态（相）之间的转换关系。自由相的DNAPL可以溶解于水中，溶解相DNAPL可以被黏土颗粒部分吸附。溶解相浓度的最大值为其在水中的溶解度。

图1 DNAPL在土中存在的三种状态Fig.1 Three phases of DNAPL in soil

自由相DNAPL在水中的溶解过程可用下式模拟：

式中：De为DNAPL在土中的分子扩散系数，m2·s-1；d50为土颗粒平均粒径，m。大量的砂土试验的结果证明，参数Sh的大小与水的流速有关［9-11］。

溶解相DNAPL吸附于土颗粒的过程用以下线性平衡吸附过程模拟：

式中：Esn/w为吸附速率，g·cm-3·s-1；ρb为土的干密度，g·cm-3；ρ为溶解相DNAPL的质量浓度，kg·m-3；Kd为吸附分配系数，cm3·g-1，吸附分配系数Kd的大小主要与土中有机质含量有关。

1.2 DNAPL迁移控制方程

DNAPL污染源在饱和黏性土中的纵向迁移主要包括两种过程：一种是自由相DNAPL以连续流体方式的迁移，这个过程受DNAPL-水毛管压力的控制，称为两相流；另外一种是DNAPL溶解于水中后在水中的迁移，也被称为溶质运移，这个过程受对流弥散作用的控制，但在静水条件下，主要受分子扩散作用的控制。根据土孔隙中各物质的质量平衡，水溶液、自由相DNAPL和溶解相DNAPL的控制方程分别为

式中：ε为土的孔隙度；Sw和Snw分别为水和自由相DNAPL的饱和度；vw和vnw分别为水和自由相DNAPL的达西流速，m·s-1；Dw为水动力弥散系数，m2·s-1；ρw和ρnw分别为水溶液和自由相DNAPL的密度，g·cm-3和分别为溶解速率和吸附速率。方程（4）和（5）构成了经典的两相流方程，方程（6）是经典的对流弥散溶质运移方程。

水动力弥散系数Dw是个二阶张量，包括机械弥散（与水的流速有关）和分子扩散（与水的流速无关）两部分，表达式为

式中：uwx、uwy和uwz为水的真实流速分量，m·s－1；|uw|为水的真实流速大小，m·s－1；αL和αT分别为纵向和横向弥散度，m，对于黏性土，典型数值为αL＝0.1～1.0 m，αT＝（0.1～0.3）αL；De为有效分子扩散系数，m2·s－1，与DNAPL的分子扩散系数以及土的结构性有关，即

式中：Daq是DNAPL在水中的分子扩散系数，m2·s－1），一般在10-10～10-9m2·s－1；ω为弯曲因子，与土的结构性有关，一般在0.1～0.5之间。

根据达西定律，真实流速uw（水）、unw（NAPL）以及达西流速vw（水）、vnw（NAPL）之间的关系可表示为

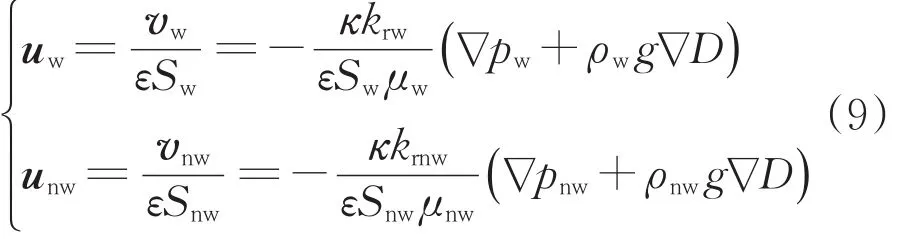
式中：κ为土体固有渗透率，m2；krw和krnw分别为水和DNAPL的相对渗透率；pw和pnw分别为水和DNAPL的压力，Pa。

毛管压力pc（=pnw－pw）、相对渗透率kr和饱和度S三者之间的关系，即kr-S-p关系，是两相流的重要本构关系。根据Parker等［12］提出的缩放理论，由van Genuchten［13］模型给出的DNAPL-水毛管压力pc与水的饱和度Sw的关系如下：

式中：β 为水-气表面张力 σaw（=72 mN·m-1）与DNAPL-水表面张力σow（mN·m-1）的比值，对于大多数DANPL，σow=30～45 mN·m-1；m和n为土水特征曲线的参数，且m=1－1/n。

采用 Mualem［14］提出的方法，由 van Genuchten模型得到的相对渗透率krw（水）、krnw（DNAPL）与水的饱和度Sw的关系

注意相对渗透系数只与参数m（m=1－1/n）有关，而和α无关。

1.3 方程求解

基于COMSOL Multiphysics软件开发了求解偏微分方程（4）～（6）的模块，需求解的变量为pw、pnw和ρ。COMSOL Multiphysics软件是一种自动有限元软件，采用有限元方法求解偏微分方程组。计算结果输出中土中自由相DNAPL的含量用饱和度表示，溶解相DNAPL的含量用浓度表示，二者均可以转化为质量分数表示，即单位质量的土（饱和土）中DNAPL的质量。

2 分析模型及基本参数

DANPL在饱和黏性土中一维迁移数值分析模型如图2所示。模拟对象为深度为10 m的均质饱和黏性土土柱。DNAPL选取氯苯，根据国家相关标准［15］规定，这种污染物在土中的筛选值为68 mg·kg－1（即0.068 mg·g-1）。土柱顶面的水压pw为0，自由相DANPL压力pnw为5 kPa（即0.5 m水头），溶解相DANPL的质量浓度ρ0为溶解度S*。土柱底面为一排水界面，水压pw维持在100 kPa。黏性土中的孔隙水并没有赋予一个流速，地下水处于静止状态。即使在自由相DNAPL的驱替下，黏性土中水的流速也非常低，这一点从后面给出的分析结果中可看出。

图2 数值分析模型Fig.2 Model of numerical analysis

计算参数分为三类：第一类为两相流方程参数，第二类为对流弥散方程参数，第三类为溶解作用参数。这些参数的取值如表1所示，所取参数值均为典型数值。土的参数选用的是沿海地区典型饱和粉质黏土的参数，孔隙度ε取0.5，固有渗透率κ为1×10－15m2（饱和渗透系数为1×10－6cm·s－1）。土的Sw-Pc模型参数取值参照Lu等［16］给出的黏土的参数的变化范围，α在0.001～0.01 kPa－1之间，n在1.1～2.5之间。对于溶解作用参数Sh=2，参照了一些学者在水流缓慢情况下得到的NAPL在砂土中的溶解速率值［9-11］。

表1 参数基本值Tab.1 Basic values of parameters

3 静水条件下溶解相DNAPL分子扩散

首先仅模拟溶解相DNAPL自土柱顶面向下迁移的过程，不考虑自由相DNAPL的两相流迁移，物理上为静水条件下的分子弥散过程。土柱顶面的边界条件为：①溶解相DANPL的质量浓度ρ0为溶解度S*；②水压力pw为0；③自由相DANPL的压力为0。

分析得到的质量分数wad（包括溶解相和吸附相，为其质量与土的总质量之比）以及溶解相的质量浓度比ρ/ρ0随深度h的变化如图3所示。在选取的参 数 值 下（De=2.9×10－10m2·s－1，Kd=3.63cm3·g－1），迁移过程是非常缓慢的，10年的最大迁移深度为0.5 m，平均每年0.05 m。溶解相DNAPL含量的最大值出现在地表，质量分数为1.4 mg·g－1，随深度的增大而减小。

有效分子扩散系数De和分配系数Kd是影响静水条件下的分子扩散的最重要的两个参数，下面分析这两个参数的取值对计算结果的影响。

3.1 有效分子扩散系数De

有效分子扩散系数De的大小决定了溶解相DNAPL分子在土中扩散的速度。统计分析结果表明，黏土中NAPL有效分子弥散系数De在（1～5）×10－10m2·s－1之间［17-19］。将De分别取 1×10－10m2·s－1和1×10－9m2·s－1，其他参数按照表1 中的对流弥散方程参数设置，计算得到的溶解相DNAPL在土中的迁移过程如图4所示。有效分子扩散系数增大10倍，DNAPL迁移速度仅增大到原来的3倍左右，10年的最大迁移深度也仅为1 m左右。

3.2 分配系数Kd

图3 静水条件下溶解相DNAPL的分子弥散Fig.3 Molecular diffusion of dissolved DNAPL under hydrostatic condition

图4 有效分子扩散系数参数分析Fig.4 Parameter analysis of effective molecular diffusion coefficient

黏土中有机质含量较高，故研究吸附作用对溶解相DNAPL迁移的影响很有必要。线性吸附分配系数Kd分别取0 cm3·g－1（不考虑吸附）和10 cm3·g－1，其他溶质运移参数为表1中给出的数值，得到的计算结果如图5所示。从图5可知，分配系数Kd越大，阻滞作用越明显，DNAPL迁移速度越慢。在不考虑吸附的情况下（Kd=0 cm3·g－1），10年的迁移深度增大到2 m左右。可见，饱和黏性土的吸附作用会显著影响溶解相DNAPL的迁移。

以上分析结果表明，水流静止条件下，加上吸附所导致的阻滞，DNAPL在饱和黏性土中的弥散迁移速度非常缓慢，十几年和几十年内不会造成饱和黏性土的深部污染。

4 连续注入下两相流-对流弥散迁移分析

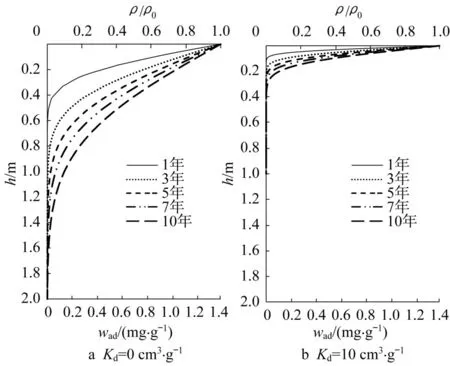
图5 线性吸附分配系数参数分析Fig.5 Parameter analysis of distribution coefficient of linear sorption

下面进行连续注入情况下的两相流与对流弥散耦合分析。采用图2所示的边界条件，在土柱顶面的自由相DNAPL施加0.5 m的水头，即5 kPa的压力（也就是约45 cm氯苯的高度）。这种情况下自由相的DNAPL会在重力作用下逐渐向下迁移。下面主要介绍分析得到的自由相DNAPL的纵向迁移规律，以及参数取值对分析结果的影响。

4.1 自由相DNAPL含量、压力以及流速

计算得到的不同时间的自由相DNAPL的质量分数wnw（自由相DNAPL的质量与土的总质量之比）和饱和度Snw随深度h的变化如图6所示。可以看出，10年后的迁移深度达到2.5 m左右，大于图3给出的不考虑两相流情况下的迁移深度，平均迁移速度为0.25 m·年－1。自由相DNAPL的饱和度在0.003以内，质量分数在1 mg·g－1以内，与前面给出的溶解态DNAPL的质量分数处于同一个数量级。尽管这个数量级是非常低的，但是仍然超出污染物氯苯的筛选值（0.068 mg·g－1）。因此，两相流迁移可能是导致深部饱和黏性土中DNAPL检出值超标的原因。

图7给出了DNAPL压力pnw、水压力pw以及毛管压力pc随深度的变化。可以看出，水压力pw几乎始终维持在静水压力，而DNAPL压力pnw则随着迁移深度的增加逐渐向深部传递。毛管压力pc决定了自由相DNAPL的饱和度。毛管压力最大值为5 kPa，出现在地表。

图6 饱和黏性土中自由相DNAPL的含量Fig.6 Content of free DNAPL in soil

图7 pnw、pw和pc随深度的变化Fig.7 DNAPL pressure,water pressure，and capillary pressure

图8 给出了vnw和vw随深度的变化。在自由相DNAPL迁移深度范围内，水的达西流速随深度的增加而增大，DNAPL的达西流速随深度的增加而减小。下面来分析造成这种现象的原因。随着深度的增大，DNAPL的饱和度减小导致相对渗透率减小，而压力梯度略有增大，因而达西流速减小。对于孔隙水，随着深度的增大，水的饱和度增大导致渗透系数增大，而压力梯度基本不变，因此水的达西流速增大。在DNAPL侵入深度以下，水的饱和度为100%而水力梯度不变，因此水的速度沿深度基本不变。

图8中给出的DNAP和水的达西流速为一个数量级，在0～0.3 mm·年－1之间，这个速度是非常小的。然而由于二者饱和度的巨大差别（自由相DNAPL的饱和度在0.003以内，而水的饱和度接近1），因此根据式（9）得到的DNAPL和水的真实流速也差别较大。图9给出了DNAPL和水的真实流速uw和unw，DNAP的真实流速达到100～200 mm·年－1，是水的几百倍，这与图6中给出的平均每年迁移0.25 m的速度是吻合的。注意DNAPL真实流速随深度的增大而增大，与达西流速随深度的变化正好相反。在DNAPL饱和度接近0的深度处，DNAPL真实速度会出现突变的现象，这是因为计算真实速度时，当式（9）分母中的饱和度接近0时得到的结果会不稳定。

图8 vw和vnw随深度的变化Fig.8 Darcy velocities of water and DNAPL

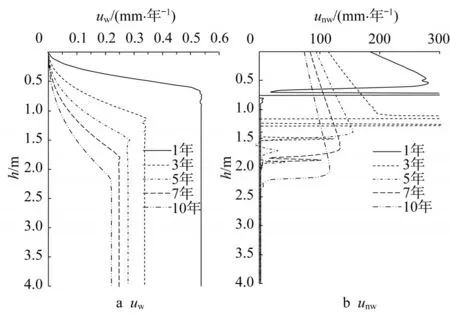
图9 uw和unw随深度的变化Fig.9 Real velocities of water and DNAPL

4.2 自由相DNAPL的溶解

为了对自由相NDAPL在土中的溶解速度有一个直观的印象，这里先分析静止条件下（DNAPL和水的流速均为0）自由相DNAPL在土中的溶解。静止条件下自由相DNAPL的溶解可以表示为

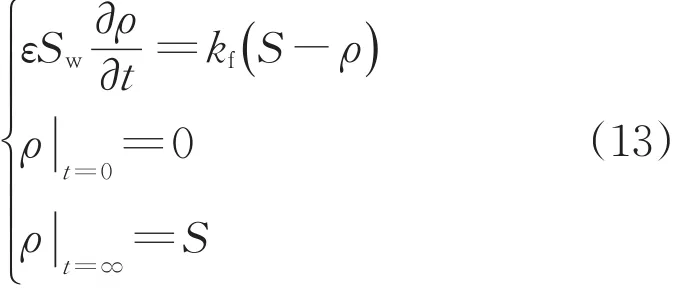
上述微分方程的解为

取氯苯的 De=3×10－10m2·s－1，黏土 d50≈0.01 mm，孔隙度ε=0.5，水的饱和度Sw=0.9，修伍德准数Sh=2，得到

令ρ（t）/S=0.999，计算得到t=0.52 s。意味着在t=0.52 s时，水中氯苯的质量浓度就达到了溶解度。溶解平衡过程是迅速的，其原因是黏土的平均粒径d50要远远小于砂土，因此按式（2）计算得到的溶解平衡速率 kf较大。Lenczewski等［20］通过实验发现，TCE（三氯乙烯）能够迅速进入富含黏土的细粒土中，并快速溶解在孔隙水中。因此可以认为自由相DNAPL在饱和黏性土中的溶解平衡过程几乎是瞬时的。

图13给出了分析得到的溶解相DNAPL在土中的分布。与图3对比可以看出，自由相DNAPL的溶解使得溶解相DNAPL的分布发生了显著的变化。在自由相DNAPL迁移深度范围内，溶解相DNAPL的质量浓度均达到溶解度。且由于机械弥散作用，10年时溶解相的最大迁移深度比自由相的（约2.5 m）还要深，达到3.0 m左右。以上分析表明，饱和黏性土中溶解相DNAPL含量受两相流和溶解作用控制，而不是对流弥散作用。两相流分析对土中溶解态DNAPL含量的分析同样非常重要。

图10 溶解相DNAPL的分布（Sh=2）Fig.10 Profile of dissolved DNAPL(Sh=2)

4.3 渗透率的影响

土体固有渗透率κ是影响自由相DNAPL迁移的一个最重要的参数，它决定了自由相DNAP的迁移速率。 将κ从1×10－15m2减小至1×10－16m2和1×10－17m2，也就是饱和渗透系数 ks从 1×10－6cm·s－1减小至 1×10－7cm·s－1和 1×10－8cm·s－1，其余参数均不变。这种渗透性的变化相当于由渗透性较大的粉质黏土变为渗透性低的压实黏土。计算得到的自由相DNAPL的迁移剖面如图11所示。

图11 固有渗透率不同取值的分析结果Fig.11 Paramter analysis of intrinsic pemibility

从图11可以看出，渗透系数降低以后，自由相DNAPL的迁移速度和迁移深度均降低。当κ减小100倍时，迁移深度减小至原来的1/10。只有当饱和黏性土的渗透率很低时，自由相DNAPL向下的迁移才会非常缓慢。对于天然饱和粉质黏土，其渗透系数往往会达到1×10－6cm·s－1的数量级，这种地层中自由相DNAPL的向下迁移是不可忽视的。

4.4 Sw-pc关系的影响

Sw-pc关系对两相流有直接的影响。改变参数α和n的数值，参数α分别取0.002 5（减小）和0.010 0（增大），参数n分别取1.2（减小）和2.0（增大）以了解Sw-pc关系对自由相DNAPL迁移的影响。计算得到的自由相DNAPL的迁移剖面分别如图12和图13所示。

从计算结果来看，参数α对DNAPL饱和度的影响较大，对DNAPL侵入深度的影响较小。参数n对DNAPL迁移速度和迁移深度影响很大，在n=1.2的情况下，连续注入10年的迁移深度可达到10 m；而在n=2.0的情况下，连续注入10年的迁移深度只有1 m。因此，迁移速度和深度对参数n的取值非常敏感。这和公式（11）是一致的，相对渗透率仅与参数n有关，而和α无关。

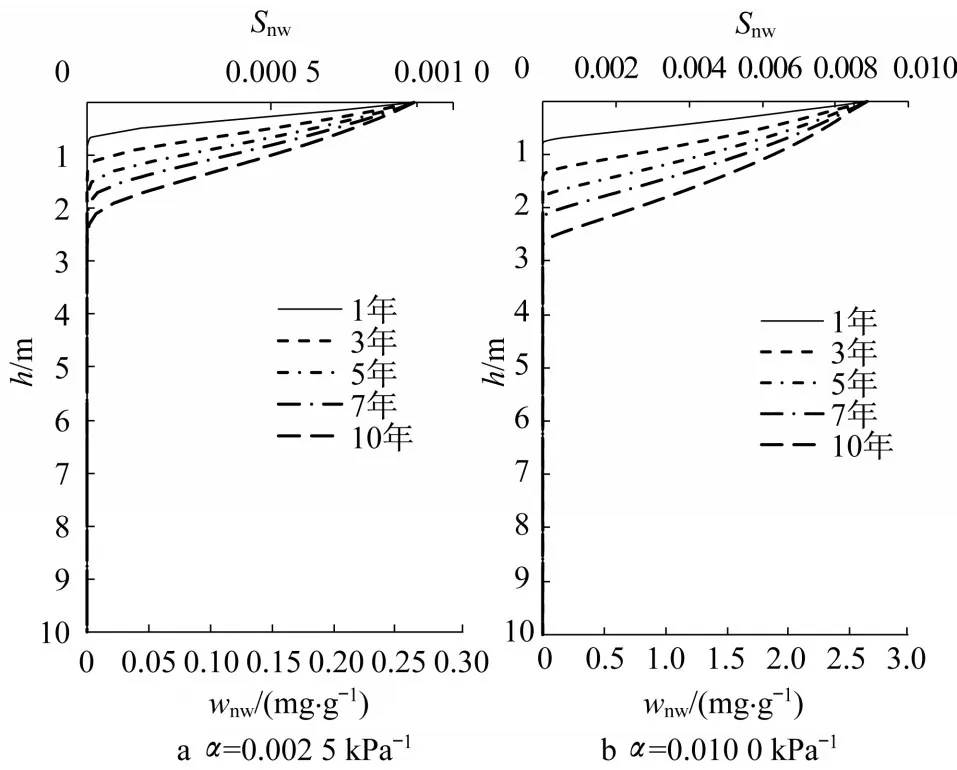
图12 参数α不同取值的计算结果Fig.12 Parameter analysis of α

图13 参数n不同取值的计算结果Fig.13 Parameter analysis of n

4.5 DNAPL污染源消失后的纵向迁移

前面分析了土柱表面DNAPL污染源在5 kPa压力下连续注入10年情况下的DNAPL迁移特性。在连续污染10年后，将土柱顶部的DNAPL压力设为0，代表工厂关闭等原因导致的污染源消失，分析得到了污染源消失后50年DNAPL在土中的迁移过程。

图14给出了污染源消失后（阶段B）自由相DNAPL的饱和度剖面，并与前期连续注入10年（阶段A）的计算结果对比。顶部污染源消失后，DNAPL完全在重力作用下继续向下迁移，最大饱和度出现的深度也逐渐下移。由于DNAPL总量基本不变，因此随着迁移深度的增加，最大饱和度逐渐减小。在第60年时最大迁移深度达到近6 m，平均迁移速度约0.08 m·年－1，比阶段A的平均迁移速度0.25 m·年－1要小一些。

图14 污染源消失后自由相DNAPL的分布Fig.14 DNAPL distribution after removing pollution source

5 结论

基于COMSOL Multiphysics软件平台，开发了DNAPL-水两相流分析以及考虑吸附、溶解作用的溶质运移分析模块，进行了均质饱和黏土中DNAPL纵向迁移过程的分析，得到了一些有意义的结论。

（1）饱和黏性土中溶解态DNAPL的分子扩散迁移过程非常缓慢，不能在几十年内造成土体深部污染。自由相DNAPL的纵向迁移速度主要受固有渗透率k以及毛管压力-饱和度关系的影响，可在一定条件下成为饱和黏性土中DNAPL竖向迁移的主控因素。

（2）毛管压力-饱和度模型中参数n以及土的固有渗透率k控制着自由相DNAPL的纵向迁移速度以及含量。尽管在低毛管压力下自由相DNAPL难以大量侵入饱和黏性土（饱和度只有千分之几），但仍然会超过污染物的环境筛选值。对于渗透系数较大的饱和黏性土地层（如粉质黏土层），这种微量的、真实流速可达每年几十厘米的流动足以造成DNAPL在几十年内迁移到十几米的深度。

以上基于数值分析得到的结论，能够初步解释一些旧农药厂厂区饱和黏性土场地中深部存在DNAPL污染的现象。关于饱和黏性土中的DNAPL-水两相流分析，仍然需要进行更为深入和系统的研究工作。