一种自适应的四轴飞行器PID控制算法

李 威,邱 霞,徐德利

(湖北理工学院 电气与电子信息工程学院,湖北 黄石 435003)

四轴飞行器因具有飞行性能良好、造价低的优点，被广泛应用于地质测绘、无人航拍等领域。四轴飞行器以PID控制算法为主，但PID参数的调节易受环境影响，远不能满足不同行业的差异化需求[1]。例如：在PID参数保持不变的情况下，当挂载重量为100 g时，飞行器飞行稳定；当挂载重量为200 g时，飞行轻微不稳定；当挂载重量为300 g时，飞行极其不稳定。因此，需要重新调整PID参数，以适应不同的载重需求，确保飞行器稳定飞行。

针对以上问题，提出了一种自适应的四轴飞行器单双环并行调节的PID控制算法，具有成本低、实时性强、数据处理率高的优点。

1 四轴飞行器硬件平台的搭建

四轴飞行器实物图如图1所示，主要由机体、电机、集成电路板和遥控器4个部分组成。电机包括4个无刷电机，分别固定于机体的4个角部上，电机输出轴上均安装有螺旋桨叶片，对角的螺旋桨叶片旋转方向一致，相邻的旋转方向不同。集成电路板上的集成飞行控制系统固定在机体上，包括三轴陀螺仪、三轴加速度传感器、数字气压传感器、GPS定位模块、超声波模块、无线模块和电子调速器。遥控器通过无线模块与飞行控制系统实现通信连接。

图1 四轴飞行器实物图

四轴飞行器通过MPU6050传感器获取飞行器的姿态数值[2]，由无线接收机获取遥控指令，经主控芯片进行数据处理并输出PWM波控制电机转动实现飞行[3-4]。在飞行过程中通过实时改变4个电机的转速配比，实现四轴飞行器上升、下降、悬停及向前、向后、向左、向右等不同姿态的飞行。

传感器在使用过程中会受到各种因素的干扰，从而导致经PID控制算法处理后的输出数据发生突变，所以传感器的输入数据必须保证平滑。因此，采用限幅滤波与低通滤波相结合的滤波方式来消除干扰。

2 PID控制算法的设计

2.1 PID控制算法简述

PID控制算法的实质是根据输入的偏差值，按照比例、积分、微分的函数关系进行运算，运算结果用以控制输出[5]。PID控制算法公式如下：

Y=P×e(k)+I×∑e(k)+D×[e(k)-e(k-1)]

(1)

式(1)中，e()为目标姿态与实际测量姿态之差;k为PID控制次数;Y为PID输出;P为比例调节参数，对偏差做出即时反应，即偏差一旦产生，调节器立即产生控制作用使被控量朝着减小偏差的方向变化，控制作用的强弱取决于比例系数的大小；I为积分调节参数，只要偏差不为零，输出就会随时间不断变化，以减小偏差，直到消除偏差，不再起控制作用，系统达到稳态；D为微分调节参数，调节偏差变化快慢，变化越快，反对作用越强，微分作用有助于减小超调，抑制振荡，让系统趋于稳定。

2.2 PID控制算法参数的设计

四轴飞行器的控制算法采用单环PID控制算法与双环PID控制算法2种方案。

2.2.1单环PID控制算法

只对四轴飞行器进行角度测量，构建单环PID控制算法，其输入为X,Y,Z三轴的角度，输出为控制4个电机转速的4路PWM波。单环PID控制示意图如图2所示。其中，θ(x,y,z)为期望角度；θ(x,y,z)measure为测量角度；y为输出4路PWM波；e(k)为第k次期望角度与测量角度之差。PID控制调节理想波形如图3所示。

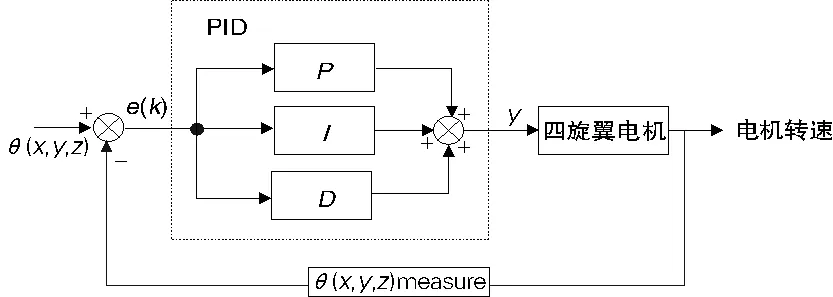
图2 单环PID控制示意图

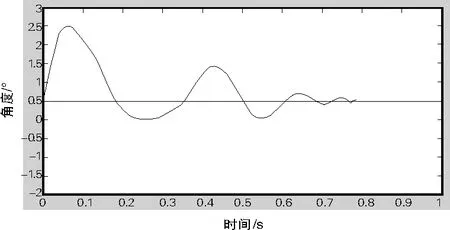
图3 PID控制调节理想波形图

通过将反馈回来的姿态角度与姿态期望角度进行对比，以修正四轴飞行器的飞行姿态期望角度，实现平稳飞行。通过调节PID控制参数，进行飞行测试并记录实验数据。单环PID控制算法的参数较优值与飞行效果见表1。

表1 单环PID控制算法的参数较优值与飞行效果

由表1可知，采用单环PID控制算法在对四轴飞行器进行飞行姿态调节时存在2个问题。

1)即使采用最优PID参数，其实际飞行效果仍然不佳。

2)飞行器飞行效果对PID参数极为敏感，仅参数P值波动±8.3%时，飞行效果就相差极大。

2.2.2双环PID控制算法

双环PID控制示意图如图4所示，分为角度PD环和角速度PID环。角度PD环的输出作为角速度PID环的期望输入[6]。其中，θ0(k)为三轴期望角度；θ(k)为三轴反馈角度；ω0(k)为三轴期望角速度；ω(k)为三轴反馈角速度；k为PID调节次数；输出为4路PWM波。实际测试的双环PID控制算法的参数较优值范围见表2。

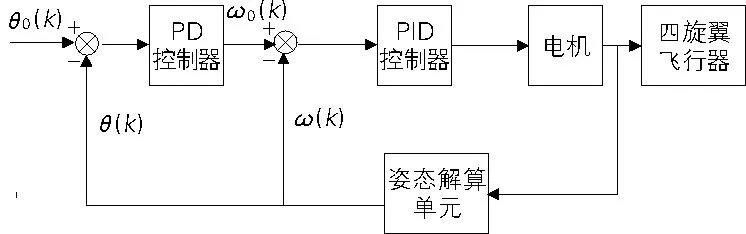
图4 双环PID控制示意图

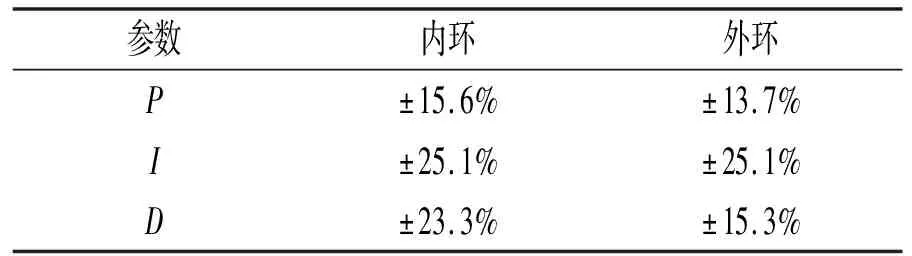
表2 双环PID控制算法的参数较优值范围

注：表中百分比范围是相对于上述飞行效果最优时对应环的PID参数而言，且每次仅改变1个参数，其他参数仍为最优值。

采用双环PID控制算法时，四轴飞行器在飞行过程中十分平稳，即使没有进行定高飞行，飞行器依旧能悬停空中。在前、后、左、右控制过程中，飞行器反应灵敏，同时在停止方向控制后经过较短时间，飞行器也会悬停。

2.2.32种控制算法的对比分析

从飞行效果上看，方案1(单环PID控制)的预期飞行效果是在发生姿态偏离正常稳定飞行状态时，飞行器能够快速进行姿态修正，保持平稳的飞行状态。但实际情况是即使在最优PID参数下，其飞行姿态也只能勉强朝一个方向倾斜，无法保持平稳的飞行状态。而方案2(双环PID控制)不仅做到了平稳起降、易于控制，且在空气气流稳定时能够实现空中悬停，飞行效果远优于方案1。

从参数较优值范围上看，在方案1中仅参数P值变化了±8.3%时，飞行器就已经无法正常飞行，而方案2中最小的参数变化范围为±13.7%，此时飞行器仍能平稳飞行，方案2的参数较优值范围远大于方案1。

通过对比分析可以发现，单环PID控制算法的参数调节不够迅速，只有当飞行器倾斜到一定角度时，飞行器才能作出反应；当飞行器倾斜角度较小时，调节无力，倾斜角度较大时反应过激，飞行不稳。而双环PID控制算法以角度调节作为外环，角速度调节作为内环，外环的角度输出作为内环角速度的期望输入。例如：当飞行器朝X轴正方向倾斜，经过角度环PD控制器调节，其输出的角速度期望为X轴负方向，使已经朝X轴正方向倾斜的飞行器具有X轴负方向的角速度，以解决飞行器飞行状态调节不够迅速的问题，确保飞行器能稳定飞行。

2.3 PID控制算法结构的设计与优化

控制算法的控制效果是由算法结构决定的，并非由单纯的PID参数决定，因此控制算法设计的核心是算法结构的设计。

算法结构的调整可以解决同一算法体系的适用性问题。要实现飞行器在挂载不同重物时依旧能稳定飞行的目标，可以通过优化算法结构完成。

2.3.1实验验证

选择风洞作为实验对象，进行验证性实验。自制简易风洞结构[7]由超声波测距传感器、透明圆筒、乒乓球、连接部和风机5个部分组成。风洞结构示意图如图5所示。

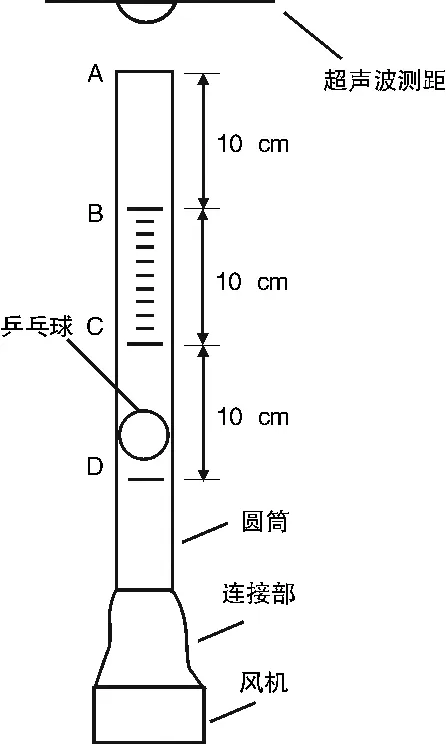
图5 风洞结构示意图

通过超声波测距实时反馈数据，单片机发出PWM波控制电机转速来实现小球悬停在指定高度。在实验过程中将乒乓球的悬停高度类比于飞行器的不同载重，PID参数的取值范围类比于系统对不同环境的适应能力，对同一硬件系统设计2种控制算法进行测试。

控制算法1：采用普通单环PID控制算法结构控制乒乓球悬停在圆筒中指定的位置高度。普通单环PID控制算法见公式(1)。

控制算法2：提出1种改进型的单双环PID控制算法，控制乒乓球悬停在圆筒中指定的位置高度。改进型单双环PID控制算法见公式(2)。

(2)

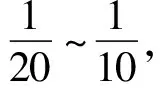
在式(2)中，比例调节和积分调节的调节强度均随期望误差e(k)的变化而变化，有利于减小调节波动，突出比例调节和积分调节各自的特点，其中比例调节有利于使控制指标快速达到期望值附近，但不利于最大程度上消除期望误差e(k)；积分调节有利于最大程度上消除期望误差e(k)，但不能使控制指标快速达到期望值，且在期望误差e(k)较大时，极易过调。

2种PID控制算法的调节波形图如图6所示。由图6可以发现，在最优参数条件下，改进型单双环PID控制算法相比于普通单环PID控制算法而言，调节时间更短，波动更小，由此再次验证了算法结构对控制效果的影响显著。改变目标高度，再次进行实验。目标高度改变时，2种PID控制算法调节情况见表3。

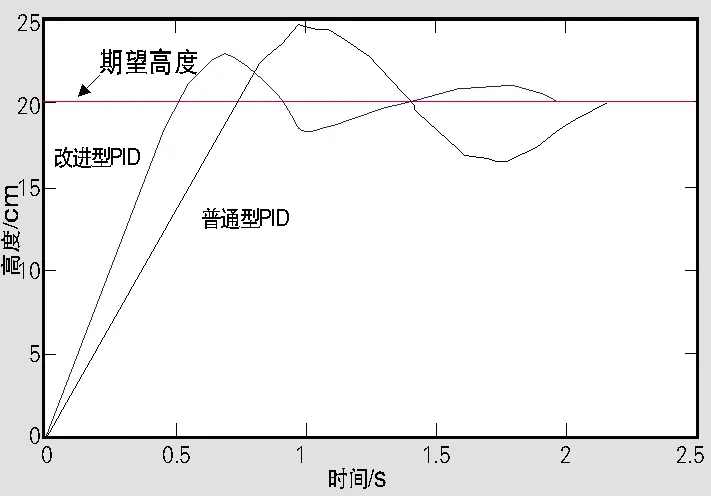
图6 2种PID控制算法的调节波形图

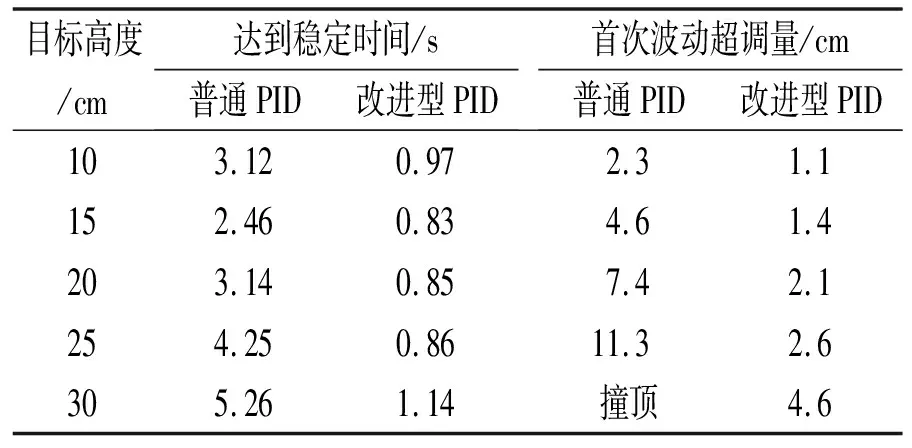
表3 目标高度改变时2种PID控制算法调节情况

注：实验数据均为多次测量取平均值。

根据表3中数据，可以得出以下结论。

1)改进型单双环PID控制算法调节过渡时间少于普通单环PID控制算法。

2)随目标高度变化，PID调节的过渡时间均有所变化，但改进型单双环PID控制算法的调节过渡时间及波动超调量均小于普通单环PID控制算法。

3)在小球高度最低和最高时，调节过渡时间明显大于中间位置，且在中间位置高度较低时，调节过渡时间最短。

取目标高度为20 cm，在保证调节过渡时间不超过4 s的前提下不断地改变PID参数进行实验，2种PID控制算法的参数较优值范围见表4。

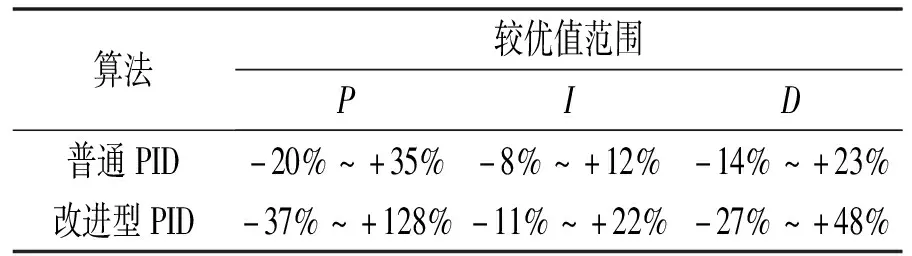
表4 2种PID控制算法的参数较优值范围

注：表中百分比范围是相对于上述飞行效果最优时对应环的PID参数而言，且每次仅改变1个参数，其他参数仍为最优值。

由表4中的数据可以发现，改进型单双环PID控制算法的参数较优值范围比普通单环PID控制算法的要大。这说明在不同的环境中，改进型单双环PID控制算法的适应性更强。

2.3.2结构优化

针对四轴飞行器的飞行特点，设计一种单双环并行调节的PID控制算法。该控制算法在飞行器的X，Y轴采用双环PID控制算法，Z轴采用单环PID调节。同时，将式(2)中的改进型单双环PID控制算法用于四轴飞行器X，Y轴的内环调节中，其外环为PD结构不变。单双环并行调节的PID控制算法的参数较优值范围见表5。在参数较优值范围内，飞行器飞行十分平稳，在前、后、左、右控制过程中，飞行器反应灵敏。

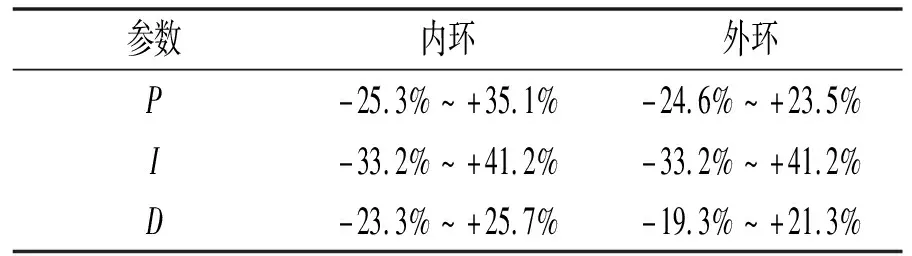
表5 单双环并行调节的PID控制算法的参数较优值范围

注：表中百分比范围是相对于上述飞行效果最优时对应环的PID参数而言，且每次仅改变1个参数，其他参数仍为最优值。

在参数最优值的条件下进行四轴飞行器的载重实验。载重实验结果见表6。

由表6可以看出，当采用单双环并行调节的PID控制算法时，四轴飞行器基本上均能保持稳定飞行，可以适应不同的载重需求。这说明改进PID的算法结构可以大大提高控制效果，增强PID控制的稳定性。

3 结论

提出了一种自适应的四轴飞行器PID控制算法。该算法集各姿态控制器为一体，采用单双环并行调节的PID控制算法，结构简单，所需数据少。与传统的使用MPU6050、电子罗盘等多种模块的四旋翼飞行器相比，该控制系统仅使用MPU6050模块，在保障抗干扰能力和恢复平衡速度相同的情况下，成本更加低廉。同时，该算法使用限幅滤波与低通滤波相结合的滤波方式，提高了数据的实时性和数据处理的效率。