基于脱靶量级数解的最优机动突防策略

王亚帆，周韬，陈万春，赫泰龙

（北京航空航天大学 宇航学院，北京100083）

基于脱靶量级数解的最优机动突防策略

王亚帆，周韬，陈万春*，赫泰龙

（北京航空航天大学 宇航学院，北京100083）

摘 要：针对比例导引控制的拦截弹，建立高阶制导系统状态空间模型，基于脱靶量级数解公式，对目标最优机动突防策略及其影响因素进行了研究。首先，针对拦截弹的制导系统为线性一阶、线性高阶时，目标最优机动突防效果进行了仿真分析，结果表明拦截弹弹体模型的准确性对突防效果存在影响，高阶系统对应脱靶量更大且效果更真实；将结果与一次阶跃机动和蛇形机动对比，发现最优机动突防效果最佳。然后，建立弹目运动的二维非线性模型，仿真得出目标最优机动产生的脱靶量曲线与线性系统吻合度较高，线性模型选取合适。最后，研究了有效导引比和剩余飞行时间估计误差对最优机动突防效果产生的影响，结果表明有效导引比估计误差对最优机动突防效果影响不大，剩余飞行时间估计误差则会使目标最优机动突防性能大幅下降，甚至部分情况比蛇形机动突防效果差。

关 键 词：突防；最优机动；脱靶量级数解；估计误差；伴随法；仿真分析

中图分类号：V221＋.3；TB553

文献标志码：A

文章编号：1001-5965（2020）01-0159-11

DOI：10.13700／j.bh.1001-5965.2019.0135

伴随法是一种计算机仿真分析与设计工具，在传统上的解释基于线性系统的脉冲响应［1］，主要运用于线性时变系统的性能分析［2-3］，能够对任意时刻的性能输出进行估计，提取显示所有输入对总性能输出的贡献信息，被广泛应用于导弹制导系统分析和设计中。比例导引是一种经典的制导律，对于追踪、截获机动目标十分有效，常应用于雷达、红外制导的导弹中［4-5］。

近年来，世界范围内，各主要国家积极推进导弹防御系统装备与技术的发展，加速拦截武器研制与部署［6］。同时，面对逐渐趋于精确化、全程化、网络化发展的拦截系统，导弹突防技术也在稳步跟进，不断注入新的内涵与方法。如何有效突破寻的导弹的拦截布防，逐渐成为研究的热点问题。针对目标的机动突防策略，相关学者做着不同方面的研究，基本的突防措施可以概括为战术突防措施、技术性措施，以提高导弹的射击精度和杀伤力［7］。在技术性突防策略上，较为常见的目标机动方式有阶跃机动［2］、蛇形机动［8］、方波机动［9］和滚筒机动［10］等，它们都是通过控制目标机动变轨，最终逃脱导弹拦截。但这些机动方式存在局限性和不稳定性，并不能保持最佳的突防效果。

Shinar和Steinberg［11］基于二维线性化模型和最优控制理论，分析了目标最优逃逸机动的控制形式是bang-bang控制且控制切换时刻与脱靶量的导数有关；对比分析了系统阶数和制导时间常数对最优机动效果的影响，同时推导得出了一阶线性系统下目标阶跃机动产生脱靶量的解析解。随后，迟泽晨等［12］以临近空间的攻防态势需求为背景，在二维平面内基于极小值原理、高斯伪谱法对高阶制导系统、攻防双方时间常数比值等因素进行研究，最终提出了一种对抗比例导引拦截器的最优机动突防控制策略。考虑到目标对拦截弹

收稿日期：2019-04-01；录用日期：2019-08-30；网络出版时间：2019-09-12 15：51

信息估计存在误差时，会对机动突防效果产生影响，Dhananjay

［13］

和Zhuang

［14］

等分别建立弹目交战的二维、三维模型，推导得出了剩余飞行时间的估计公式，探讨其对目标突破比例导引制导导弹拦截效果的影响；Nesline和Zarchan

［5］

则分析对比了剩余飞行时间估计误差存在时，经典制导律和现代制导律的鲁棒性、易用性等性能。但这些研究较难实现针对拦截弹为线性高阶制导系统时，目标最优机动突防的快速分析和求解。

本文针对高阶线性化的比例导引拦截弹制导系统，结合脱靶量级数解公式，研究了目标的最优机动突防策略问题。首先，建立拦截弹制导系统状态空间模型，基于伴随法和最优控制理论，求解目标最优机动突防策略和最大脱靶量公式；进而，考虑到最优机动突防策略的实用性，分析了拦截弹的阶数、系统是否线性和有效导引比估计误差、剩余飞行时间估计误差对策略效果的影响，并将突防效果与目标做阶跃机动、蛇形机动对比。通过上述研究，为实际攻防作战中，目标有效快速地实现最佳突防提供有价值的参考。

1 目标最优机动突防策略

1.1 比例导引制导的拦截弹一般高阶系统线性化模型状态空间描述

考虑平面内导弹-目标迎头交战模型，导弹采用比例导引制导律，即指令加速度nc＝NVcλ·（N为有效导引比；Vc为弹目接近速度；λ·为视线角变化率）。以一般的高阶线性制导系统为例，传递函数可表示为

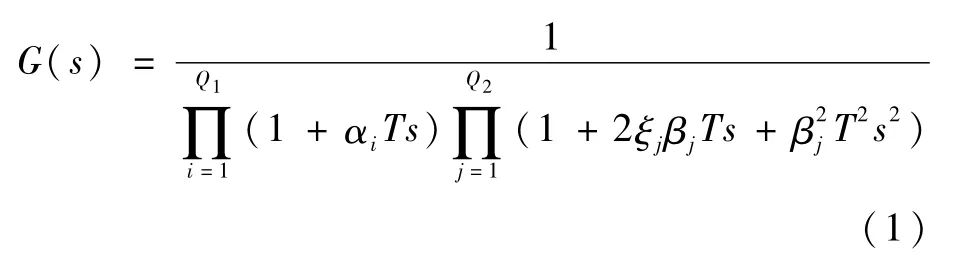
式中：αi、ξj和βj为各个环节特征参数系数；T为制导系统时间常数。传递函数G（s）包含Q1个一阶环节和Q2个二阶环节。将G（s）的分母展开为关于s的多项式可得

其中：Q＝Q1＋2Q2；λ0，λ1，…，λQ为多项式系数，由αi、ξj和βj唯一确定。

则该制导系统的线性化模型可以表示为如下状态空间形式：

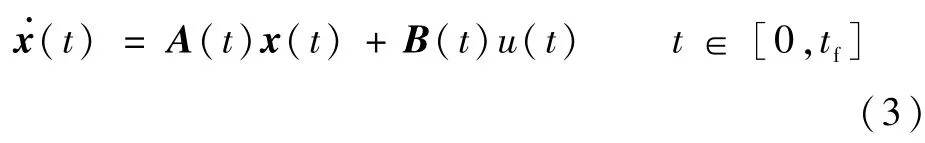
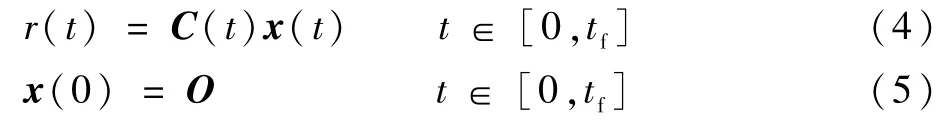
式中：t为当前时间；x（t）为状态向量；u（t）为控制输入变量；r（t）为输出变量；O表示相应维数的零矩阵；tf为总飞行时间；A（t）、B（t）和C（t）为线性系统的系数矩阵，具体为

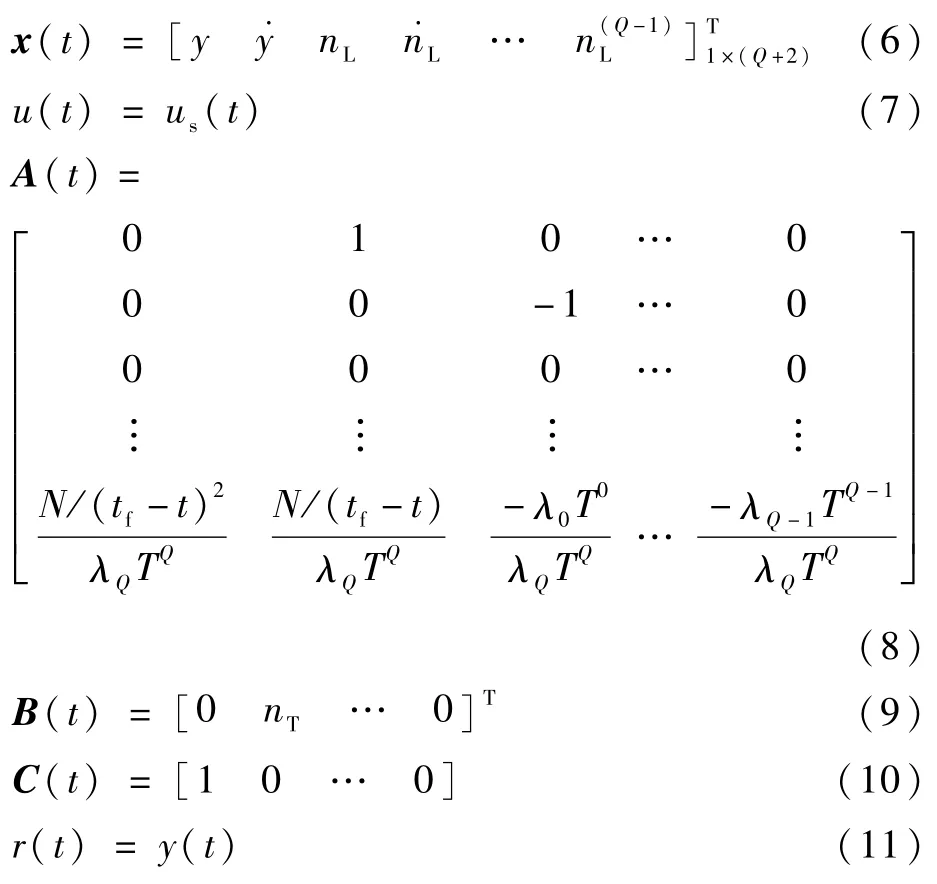
式中：y（t）为弹目相对距离在参考线垂直方向上的分量；nL（t）为导弹实际获得加速度；（t）为nL（t）的一阶至（Q－1）阶导数；us（t）为单位阶跃函数；nT为目标阶跃机动加速度幅值；y（tf）为脱靶量；N和tf均为常数。

为了讨论方便，将阶跃输入转化为脉冲输入函数δ（t），引入新的状态变量xu（t）＝us（t），利用单位阶跃函数与δ（t）之间关系可得

系统（3）和系统（4）可分别等价扩展为

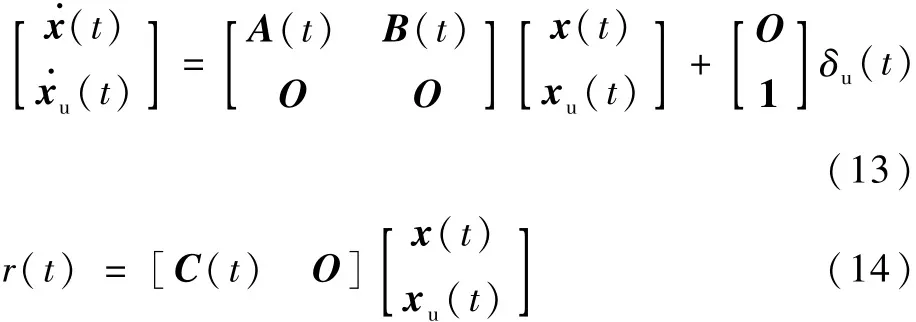
式中：δu（t）为脉冲输入函数。

1.2 伴随法推导目标阶跃机动产生的脱靶量级数解

利用伴随系统构造原则［2］，可以得到线性系统（13）和系统（14）的伴随系统状态空间描述为

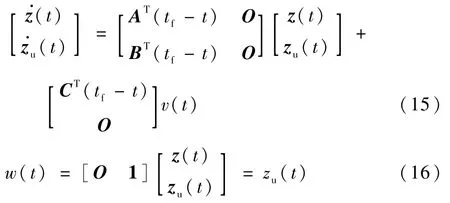
式中：z（t）和zu（t）为伴随系统的状态向量；v（t）为伴随系统的控制输入；w（t）为伴随系统的输出变量。选取该伴随系统初始状态为零，输入v（t）＝δ（t），进行伴随仿真，此时伴随系统展开等价于如下线性系统：

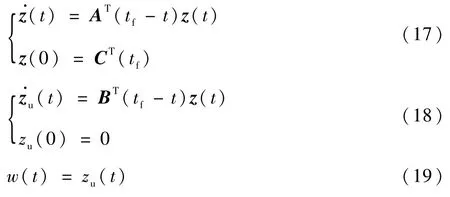
将式（17）～式（19）代入相应的系数矩阵，可得到如下微分方程：

同时，伴随系统与原线性系统输出之间存在如下关系［2，15］：

式中：tgo为导弹的剩余飞行时间，即tgo＝tf－t。

则通过对伴随系统状态变量zu（t）的求解，即可得到原系统对应脱靶量。

当导弹制导系统的传递函数为一般高阶系统，即时，参照文献［16］，可将由目标阶跃机动引起的脱靶量解析表达式写为如下幂级数形式：

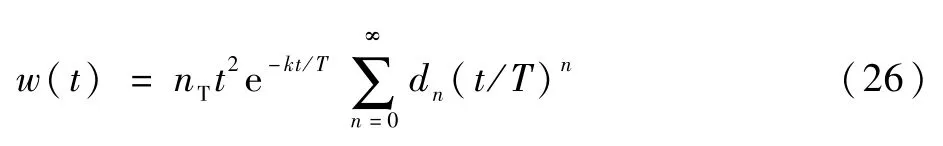
式中：k为指数项衰减常数；n为需计算的项数；dn为各级数的待定系数。

式（26）的导数式为

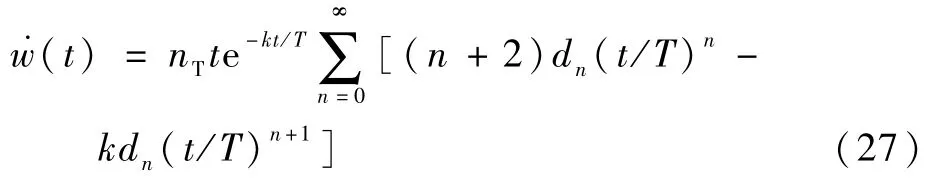
式中：各级数的待定系数dn存在以下递推关系：

当n≥1时，有

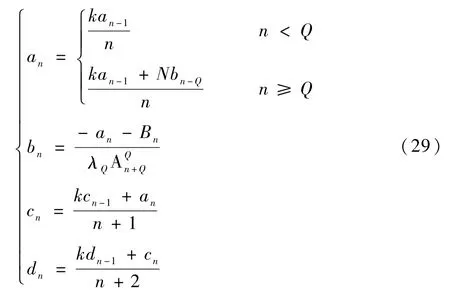
其中：

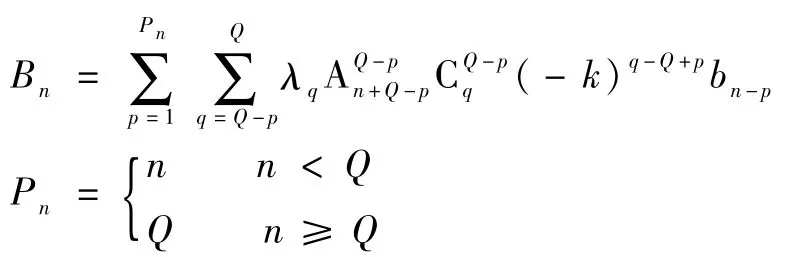
式中：an、bn、cn、Bn和Pn均为各级数系数计算的中间变量；A和C及其上下标分别表示排列数和组合数。

观察幂级数公式（26）可知，指数项衰减常数k和计算项数n影响公式的收敛速度和计算精度。由文献［16］可知，参数k的选取方案为：一阶制导系统选取k＝1，Q阶二项式系统选取k＝Q，对一般的高阶系统选取

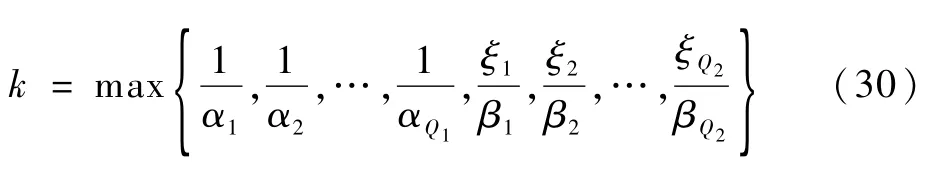
但考虑到公式的收敛速度，k取值一般不超过10。参数k选取后，计算项数n由级数收敛速度指标变量ncr确定，即

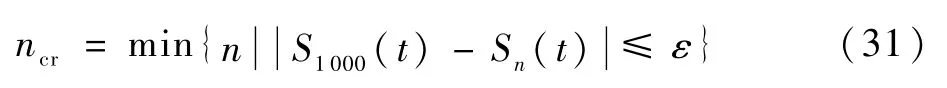
式中：S1000（t）为前1001项的部分和，其为计算的精确解；Sn（t）为前（n＋1）项的部分和；ε为指定的计算精度。由式（31）可以看出，ncr取值越小越好，意味着级数解公式的收敛速度越快。

同时，脱靶量级数解公式的收敛半径为无穷大［16］，故在仿真时间区间［0，tf］内，可以用部分和Sn一致逼近脱靶量的真实解，且只要n足够大，理论上可以以任意精度逼近。

1.3 最优机动突防策略

现在考虑目标最优机动突防问题，这里最优指的是从目标的角度出发，使脱靶量达到最大的目标机动即为最优机动。

将最优机动突防问题抽象为最优控制问题［17］：终端时间固定（tf已知），存在控制边界约束，性能泛函为即期望导弹的脱靶量达到最大。

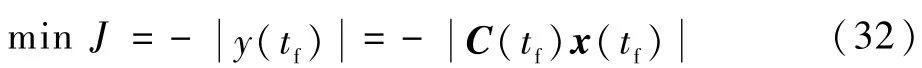
由Shinar和Steinberg［11］的推导过程可知，最优机动突防控制问题中的协态变量等于目标阶跃机动脱靶量伴随分析中伴随状态变量在时间推进上反向变换，且控制形式为bang-bang控制。

则目标机动突防时，其最优控制可以表示为

或者表示为关于剩余飞行时间的函数：

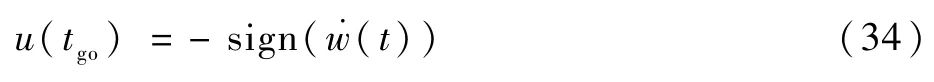
由式（33）和式（34）可知，最优突防机动控制切换函数的解析表达式正是目标阶跃机动的脱靶量导数，利用1.2节推导得出的脱靶量级数解公式计算导数.w（t）的符号，就可以直接确定当前最优机动加速度的控制符号，进而求得最优控制切换时刻。再者，最优机动突防的解u（t）可以表示为多个阶跃输入的线性组合，由线性系统输入输出的叠加原理，最优机动产生的脱靶量可由各个阶跃机动单独作用引起的脱靶量线性叠加得到。

2 弹体模型准确度对目标最优机动突防策略效果的影响

基于1.2节的脱靶量级数公式和目标最优机动突防控制表达式，考虑到拦截弹弹体模型选取的不同，会对目标突防效果产生影响，故针对不同的导弹制导系统模型进行仿真对比。

为更加直观地对比目标机动产生的突防效果，这里提出“突防成功百分比”的概念，即选定仿真的总飞行时间tf的变化范围为［tf0，tfn］，如若在某一总飞行时间tfi下，目标机动产生脱靶量的数值超过了突防成功标准线数值，则认为突防成功。突防成功百分比为tf0）。突防成功百分比越大，则认为目标在选定的仿真时间段内，机动突防的效果越佳。

2.1 假设拦截弹制导系统为一阶模型时最优机动突防策略的突防效果

针对一阶系统的仿真，选取目标阶跃机动加速度nT＝29.4 m／s2，有效导引比N＝4，T＝1 s，tfmax＝10 s，指数衰减常数为k＝1。由脱靶量级数解的系数公式（29）可知，一阶系统下，当所取的计算项数n≥N－2，即n≥2时，dn≡0，级数解公式求得结果与伴随仿真所得结果是完全一致的。

利用级数解公式仿真得到导弹脱靶量w（t）及其导数.w（t）关于剩余飞行时间tgo的曲线；注意到bang-bang控制规律是依据.w（t）的符号来确定的，从而得到最优控制u（t）与飞行时间t的关系，如图1所示。

结合图1，最优突防机动的解u（t）可表示为

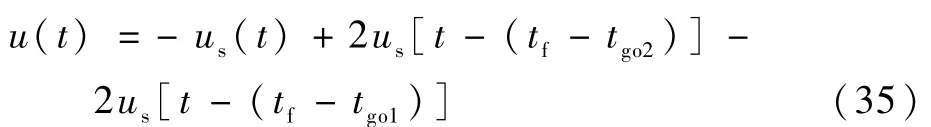
最大脱靶量可表示为

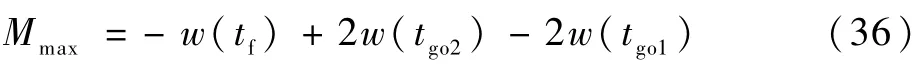
进而，分别取有效导引比N为3、4和5，得到最优机动切换时刻tgo，对应脱靶量输出w（t）以及终点时刻（tf＝10 s）脱靶量Mmax，如表1所示。

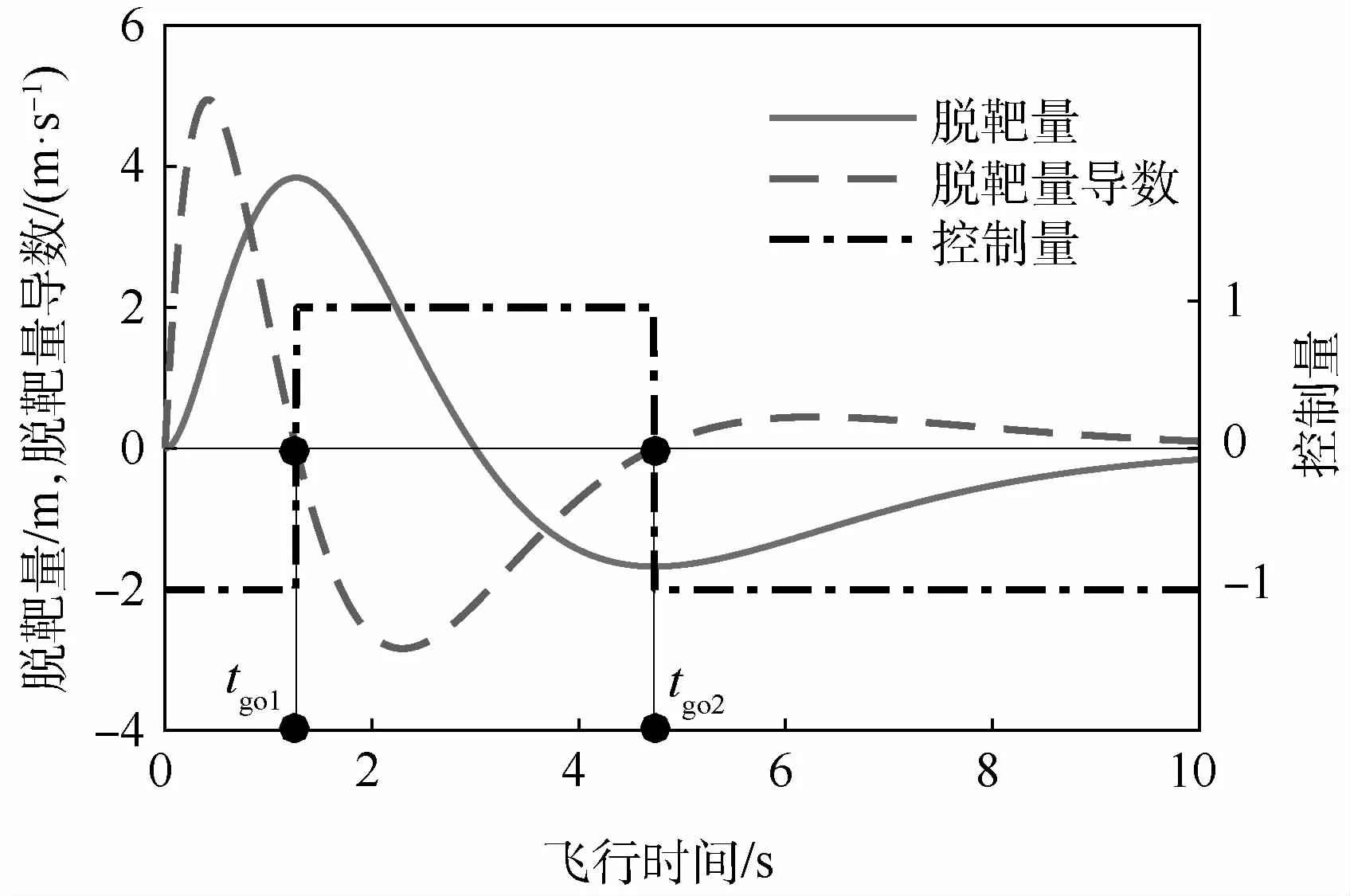
图1 一阶系统目标最优机动突防（N＝4）Fig.1 Target optimal maneuver penetration of first-order system（N＝4）

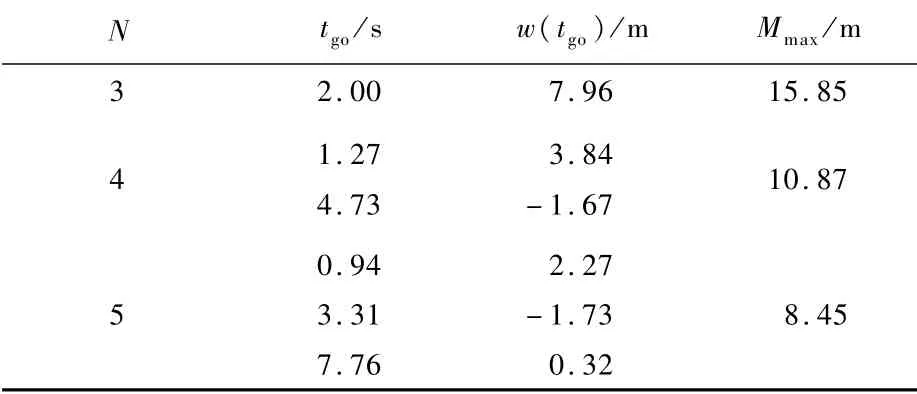
表1 一阶系统最优控制切换时刻及最大脱靶量Table 1 Op tim al control sw itching time and m axim um miss distance of first-order system

从表1可以看出，目标最优机动突防bangbang控制切换次数与有效导引比N有关。实际上当总飞行时间足够长时，bang-bang切换次数等于脱靶量导数.w（t）中多项式部分的实正零点个数，对于N为正整数情形，切换次数（实正零点个数）为N－2，且最大脱靶量的计算表达式与控制的正负值相关。

选择目标做阶跃机动的加速度表达式为

式中：aT为加速度幅值，取29.4m／s2。

目标做蛇形机动时［8］，机动是周期性进行的，大大增加了目标突防成功的几率；当机动频率和制导系统时间常数的乘积在1附近时，产生的脱靶量最大。故选择蛇形机动的频率ωT为1 rad／s，表达式为

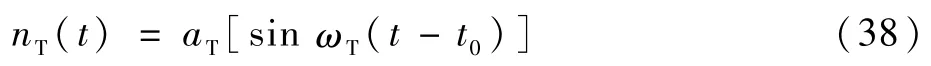
式中：t0为机动开始时刻，取0。

由式（35）的最优控制表达式和式（36）的最大脱靶量表达式，仿真得到目标最优机动产生的脱靶量随飞行时间的变化关系，并将其与目标做一次阶跃机动（式（37））和蛇形机动（式（38））产生的脱靶量作对比，如图2所示。

当飞行总时间在［0，10］s内变化时，假设以脱靶量10 m 作为突防成功的评判标准，可以看到，阶跃机动和蛇形机动在整个时间段内突防成功百分比为零；拦截弹为一阶系统时，目标做最优机动突防成功百分比仅有38%，且所需的总飞行时间较长，整体来看突防效果不佳，但仍优于阶跃机动、蛇形机动情况。由此，考虑拦截弹模型的准确性会对目标机动突防效果产生影响，选取拦截弹制导系统为高阶时进行仿真研究。

图2 一阶系统目标机动产生脱靶量对比曲线（N＝4）Fig.2 Miss distance contrast curves of first-order system for targetmaneuver（N＝4）

2.2 假设拦截弹制导系统为高阶模型时最优机动突防策略的突防效果

基于一阶系统的仿真过程，取相同的仿真参数，针对系统传递函数为五阶二项式，即G1（s）＝1／（1＋0.2s）5的情况。由式（30）、式（31）取指数项衰减常数为k＝5，计算导弹脱靶量级数公式的前80项和，仍以N＝4为例，得到级数解与伴随仿真结果的对比曲线如图3所示。

由图3可得，级数解结果与伴随仿真结果完全重合，按式（30）、式（31）所选取的参数合适，且计算精度高。

进而将目标做最优机动的突防效果，与其做阶跃机动、蛇形机动进行对比，如图4所示。

对于导弹的制导系统为五阶二项式时，可得到同式（35）的目标最优控制表达式，按此控制做最优机动产生的突防效果最佳。以脱靶量10 m作为突防成功标准时，最优机动突防成功百分比为91.4%，阶跃机动和蛇形机动的突防成功百分比分别为47.7%和75.8%；以脱靶量30 m作为突防成功标准时，3种机动方式的突防成功百分比分别为76%、0%和42.2%；最优机动突防效果明显。极限来看，当总飞行时间为2 s甚至更小时，阶跃机动产生的脱靶量几乎和最优机动一致；在总飞行时间较大时（≥4 s），蛇形机动的脱靶量明显大于阶跃机动，且与最优机动相对差别较小，但其性能不稳定。

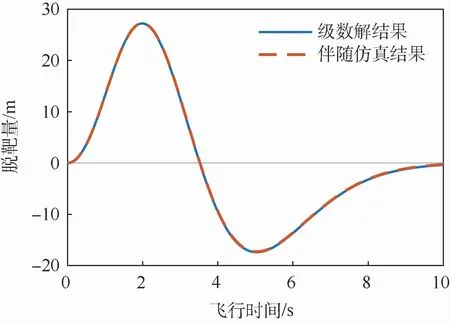
图3 五阶二项式系统目标阶跃机动产生脱靶量级数解与伴随仿真结果对比曲线Fig.3 Contrast curves between miss distance power series solutions of fifth-order binomial system due to target step maneuver and adjoint simulation results

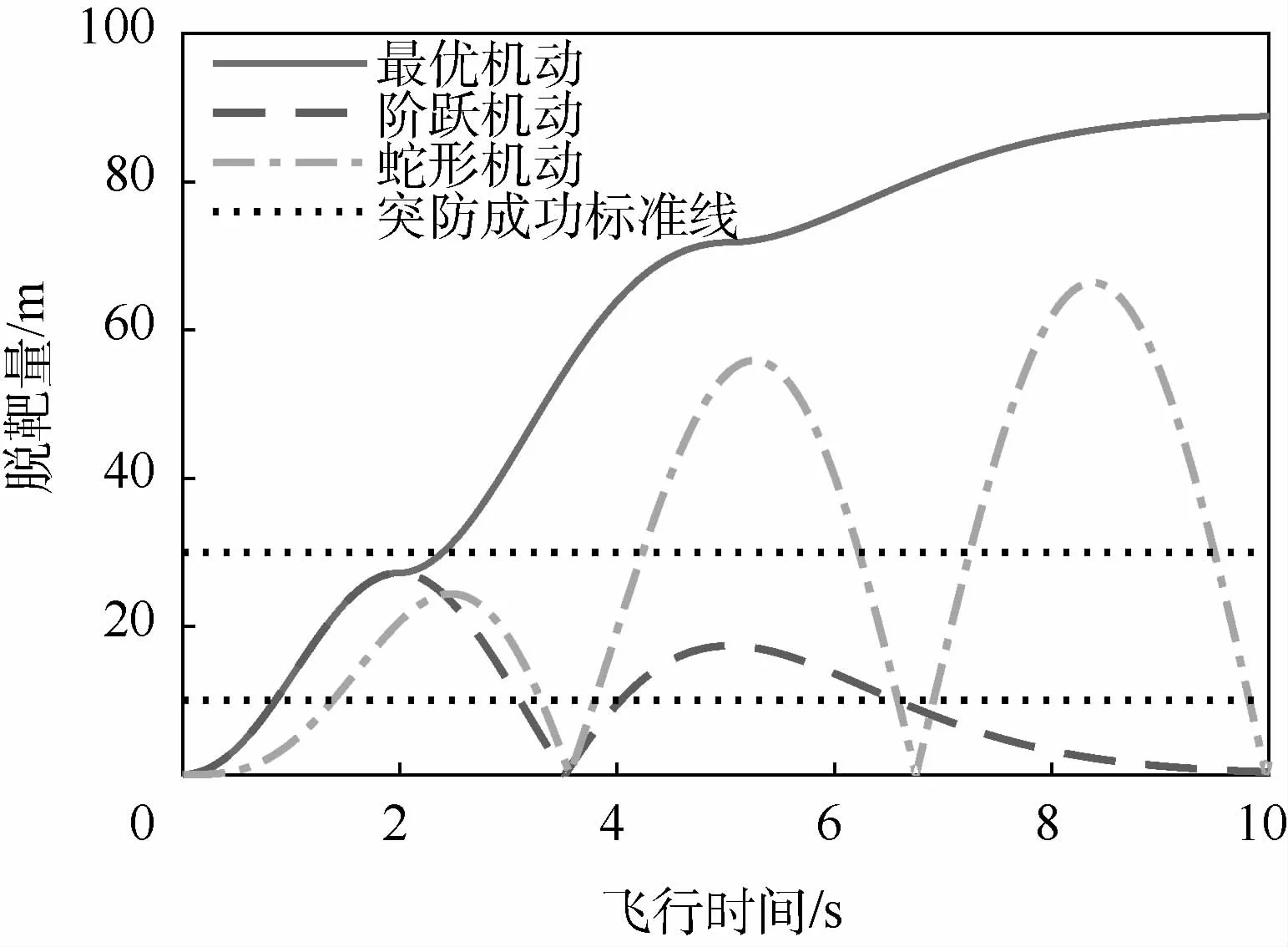
图4 五阶二项式系统目标机动产生脱靶量对比曲线Fig.4 M iss distance contrast curves of fifth-order binomial system for targetmaneuver

对比图2和图4可知，设定目标的机动幅值相同，面对导弹制导系统阶数不同时，产生的突防效果有明显差异，高阶系统的脱靶量要远大于低阶系统，且目标突防成功百分比较大。

为使问题研究更加准确，对弹体模型仿真更为精确，选择导弹的制导系统为各环节时间常数不同和带有一个二次多项式环节（其表达式分别为式（39）、式（40），系数取值如表2所示）的情况［2］，分别进行仿真。针对导弹制导系统的传递函数为G2（s）、G3（s）时，选取级数解的指数项衰减常数为k＝9，计算项数为n＝80。所得导弹脱靶量级数解结果与伴随仿真结果对比曲线如图5所示。发现级数解与伴随仿真结果完全吻合，计算精度高。

将导弹的制导系统为上述3种高阶模型下，目标做最优机动时，所产生的脱靶量进行对比，如图6所示。

表2 传递函数系数Table 2 Transfer function coefficient

图5 高阶系统目标阶跃机动产生脱靶量级数解与伴随仿真结果对比曲线Fig.5 Contrast curves between miss distance power series solutions of high-order system due to target step maneuver and adjoint simulation results

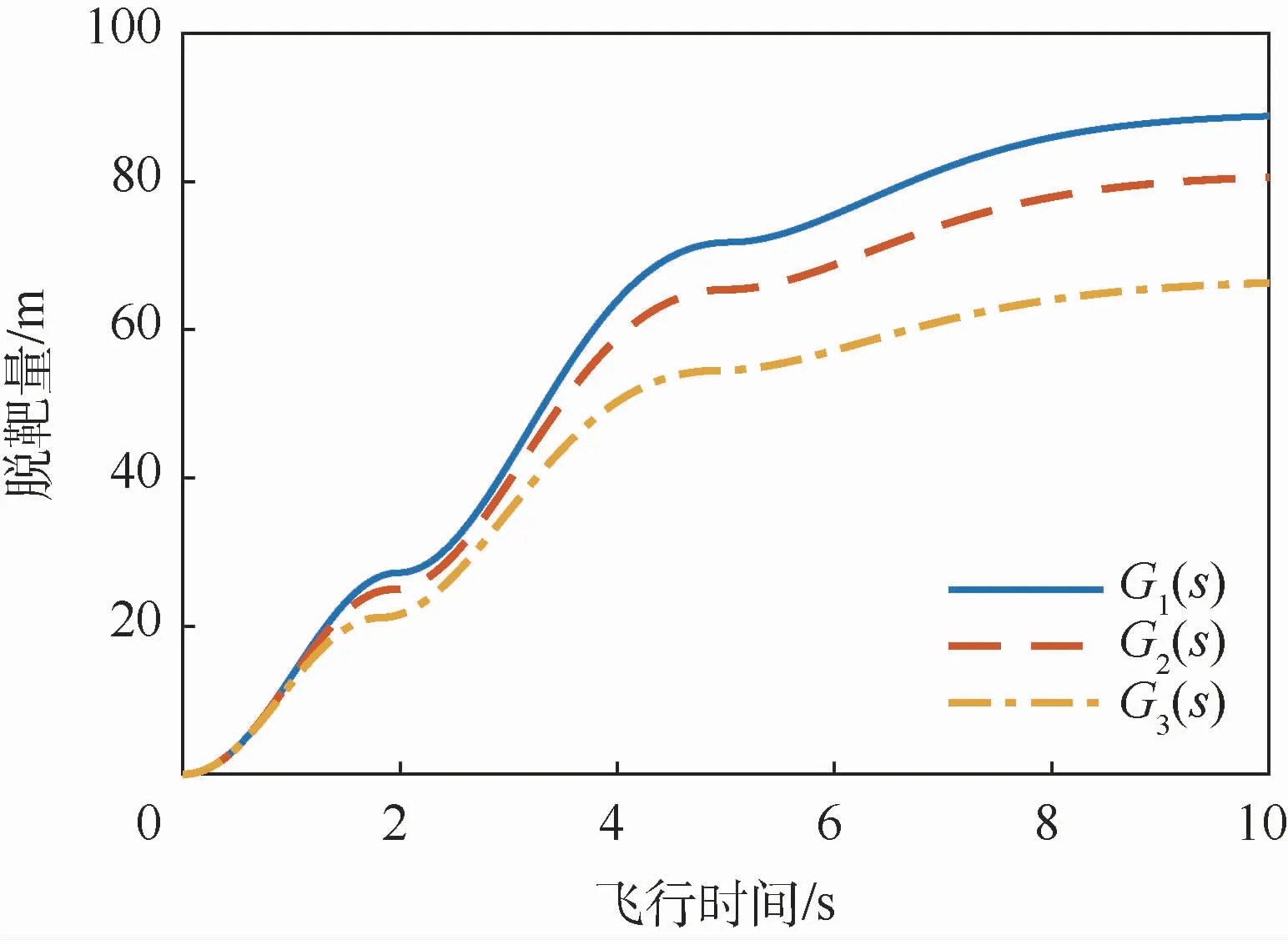
图6 高阶系统目标最优机动脱靶量对比曲线Fig.6 Miss distance contrast curves of high-order systems for target optimal maneuver

导弹的制导系统分别为上述3种形式时，目标最优机动产生的脱靶量与飞行时间的关系变化趋势类似，这是由于各情况下总的时间常数相同，均为T＝1 s。但同一时刻下，各曲线对应脱靶量值不同，以总飞行时间tf＝10 s为例，3种制导系统对应的脱靶量分别为88.84、80.58、66.33 m。可以看出，若导弹制导系统为五阶二项式形式，仿真所得结果较为乐观，目标更易突防成功，随着导弹模型复杂程度提高，目标最优机动突防效果逐渐变差，说明真实的导弹模型对目标威胁性更大。极限来看，当总飞行时间为2 s以内时，3种制导系统下，目标最优机动产生的脱靶量相差微小。

2.3 拦截弹制导系统为线性与非线性时最优机动突防策略的效果

本文的理论推导和实例仿真都是将系统简化为线性系统进行的，而实际的导弹制导系统是一个十分复杂的非线性系统，在应用中需要考虑一些微小状态量的变化对目标突防性能的影响。

由此，建立导弹、目标运动的二维非线性模型［2］。RT1、RM1分别为目标、导弹的运动距离在水平轴上的分量，RT2、RM2分别为目标、导弹的运动距离在垂直轴上的分量，VT1、VM1分别为目标、导弹的速度在水平轴上的分量，VT2、VM2分别为目标、导弹的速度在垂直轴上的分量，其导数式为

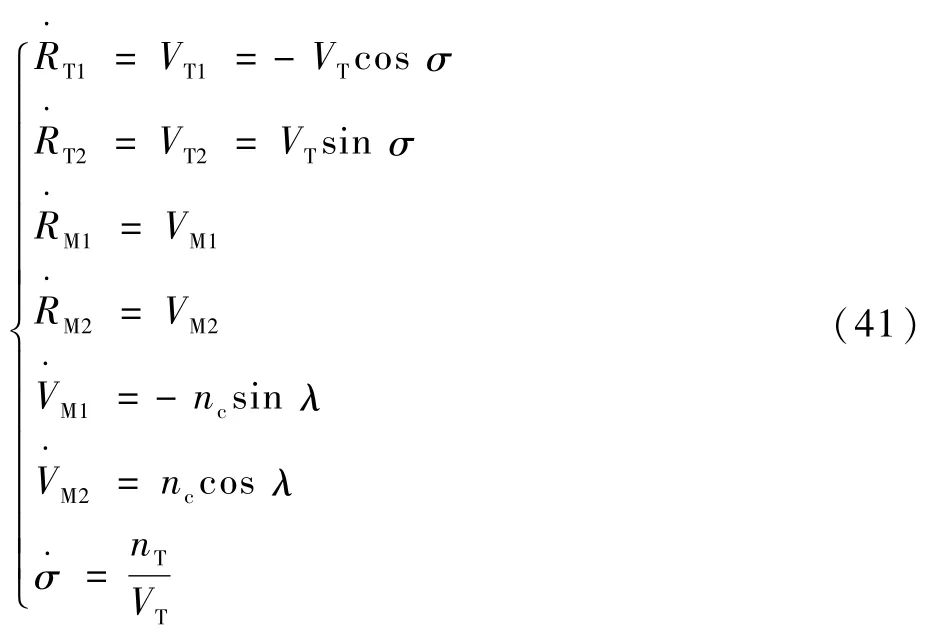
式中：σ为目标速度与坐标系x轴负方向的夹角；λ为视线角；nc为导弹的指令加速度。

进而，弹目的相对距离RTM，接近速度Vc，视线变化率λ·，剩余飞行时间tgo，导弹的指令加速度nc的表达式为

式中：下标TM 表示目标的相应变量减去导弹的相应变量；下标1、2分别表示变量在x轴、y轴的投影。

则最终导弹的脱靶量为

仍以导弹的有效导引比N＝4为例，五阶非线性系统（传递函数为G3（s））基于上述弹目间的几何运动关系以及文献［1］中的非线性碰撞三角形进行仿真。选取弹目的仿真参数如表3所示。得到线性系统与非线性系统目标最优机动产生的脱靶量与总飞行时间的关系曲线如图7所示。

导弹的制导系统为非线性，选取目标机动控制切换时刻与线性系统相同时，产生的脱靶量随飞行时间的变化趋势同线性系统基本一致，且数值接近，误差较小，说明线性模型在目标最优机动问题的研究上有较高精确度，模型选取合适。

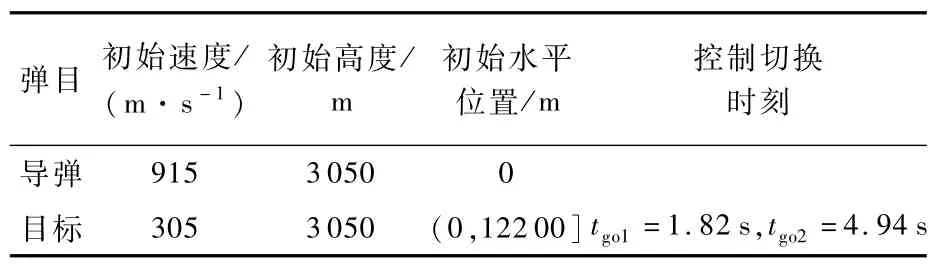
表3 弹目仿真参数Table 3 Sim u lation parameter of missile and target

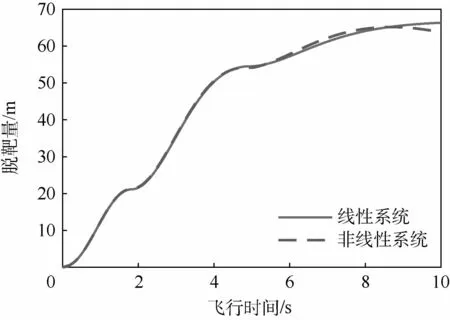
图7 线性最优机动和非线性最优机动脱靶量对比Fig.7 M iss distance comparison between linear and nonlinear optimal maneuver

观察到在最大的总飞行时间范围内（tf＝9～10 s），线性、非线性系统的脱靶量存在相对较大的偏差，这是因为利用RTM／Vc来估算剩余飞行时间tgo会存在舍入误差，切换时刻发生时可能不是真实最优。再者，仿真运行至该时刻，目标已完成两次机动，脱靶量为最终的线性叠加结果，误差也随之发生了叠加。但这些偏差不影响曲线的整体变化趋势。

3 拦截弹信息估计不准确对目标最优机动突防策略效果的影响

在实际的弹目作战中，目标需要利用导引头或告警装置较为准确地探测到来袭导弹的距离、速度等参数信息，如此才能使突防达到更好的效果，顺利逃脱导弹的打击。而雷达或红外探测装置往往易受到外界环境的影响，使得到的探测信息不准确，响应不及时，最优的切换时刻较难把握。

3.1 估计拦截弹的有效导引比存在误差

针对比例导引制导的导弹，制导指令中的有效导引比N是一个常值系数，其取值大小直接影响系统稳定性［18］；同时结合2.1节的分析，其影响最优控制切换点的个数和时刻的选取。因此，对拦截弹的有效导引比估计准确性直接影响目标最优机动突防的效果。

基于2.2节的仿真，假设目标通过告警系统探测，认为拦截弹的有效导引比N＝4，从而计算出最优的机动切换时刻tgo1＝1.82 s，tgo2＝4.94 s，实现最佳突防。而实际上目标对来袭导弹信息的估计存在偏差，研究有效导引比估计误差存在时，对目标最优机动性能的影响，如图8所示。

图8中，横坐标为拦截弹真实的有效导引比，纵坐标为目标按照拦截弹N＝4计算所得机动突防策略所产生的对应末端时刻脱靶量。观察发现，有效导引比估计误差存在时，当总飞行时间较小，目标最优机动产生的脱靶量与有效导引比呈线性负相关；当总飞行时间较大时，二者关系呈抛物线变化。若误差大致控制在±0.3左右时，对目标最优机动突防的效果影响不大；若超出这个范围，则突防性能不稳定，脱靶量会有小范围上升趋势，但整体呈下降分布，原因是目标最优机动切换次数和切换时刻的选择与拦截弹的有效导引比有关，当存在较大的估计误差时，此时的最优切换时刻并不是真实最优的，通过线性叠加，脱靶量值较最优机动存在上下波动。

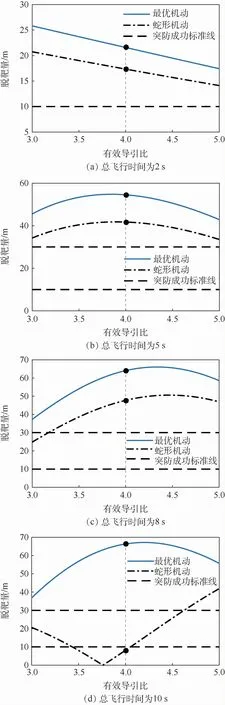
图8 有效导引比存在估计误差时目标机动产生脱靶量Fig.8 Target maneuver miss distance when effective navigation ratio estimation error exists

而蛇形机动的突防效果仍差于即使最优机动有效导引比存在估计误差的情况，且突防效果不稳定。相对来说，有效导引比估计误差存在时，对目标最优机动突防性能影响不大，在2种突防成功标准线限定下，最优机动能实现100%的突防成功百分比。

3.2 估计剩余飞行时间存在误差

注意到目标最优突防机动式（33）中需要知道导弹制导系统时间常数T（或带宽）和当前的剩余飞行时间tgo，二者共同影响最优机动控制切换时刻的选取。时间常数T的存在是由于制导系统各个环节在实际中会存在时间延迟，较难做到立即响应，该值会直接影响脱靶量的大小。而目标通常不能准确得到这两者的信息。

本节考虑T和tgo存在估计误差时，目标依然使用式（33）进行机动，来研究这些误差对机动突防性能（脱靶量）的影响。实际上，这些估计误差将会导致bang-bang控制切换时间发生变化，是tgo／T整体在起作用。本节算例中取制导系统时间常数为T＝1 s，只考虑tgo对估计误差的影响，有效导引比取N＝4，目标阶跃机动加速度幅值仍取nT＝29.4m／s2。

考虑如下形式估计剩余飞行时间：

式中为估计剩余飞行时间；tgo为实际剩余飞行时间；esf为标度系数误差；eb为零偏误差。这里主要研究esf和eb对机动突防性能的影响，且只考虑2个参数的变化不同时发生的情况。此时目标仍采用最优突防机动的表达式，只是估计的剩余飞行时间，即目标的机动规律变为

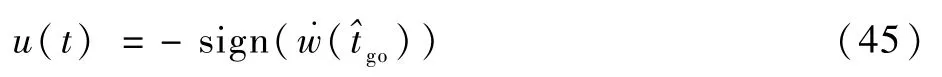
针对2.2节中制导系统传递函数为G3（s）进行分析。基于伴随系统，仿真得到脱靶量输出w（t），导数以及最优机动的bang-bang控制规律u（t）如图9所示。图中的曲线穿过“0轴”2次，故多项式存在2个零点，结合式（34）可知，目标最优控制要经过2次切换，切换时刻分别为第1.82 s和第4.95 s。

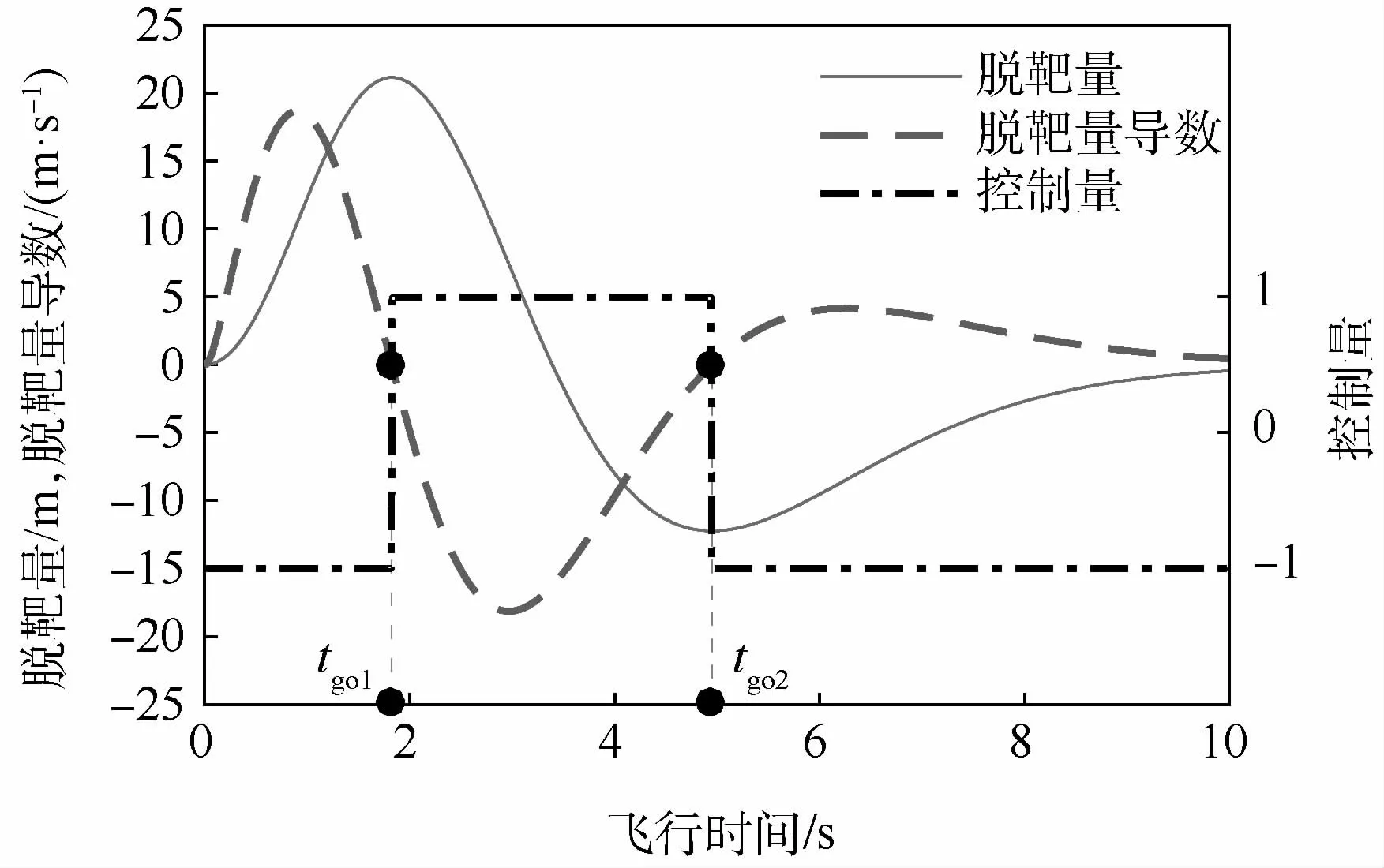
图9 高阶系统目标最优机动突防（G3（s），N＝4）Fig 9 Target optimal maneuver penetration of high-order system（G3（s），N＝4）

当估计剩余飞行时间存在标度系数误差时，适当选取esf的变化范围为［0.6，1.6］，飞行总时间tf＝10 s，得到目标做最优机动时，各误差系数对应的导弹脱靶量，如图10所示。进而，选取样本点esf为0.8，1.3，设定仿真总飞行时间在［0，10］s变化，得到脱靶量结果如图11所示；最优控制切换时刻取值及tf＝10 s时的脱靶量如表4所示。

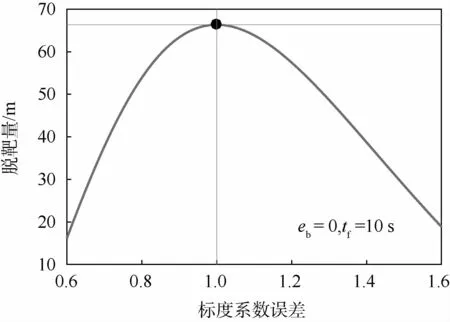
图10 目标最优机动脱靶量关于剩余飞行时间标度系数误差的曲线Fig.10 Curves of target optimal maneuver miss distance relative to scale factor error of time to go

图11 标度系数误差存在时目标最优机动产生脱靶量Fig.11 Target optimal maneuver miss distance when scale factor error exists

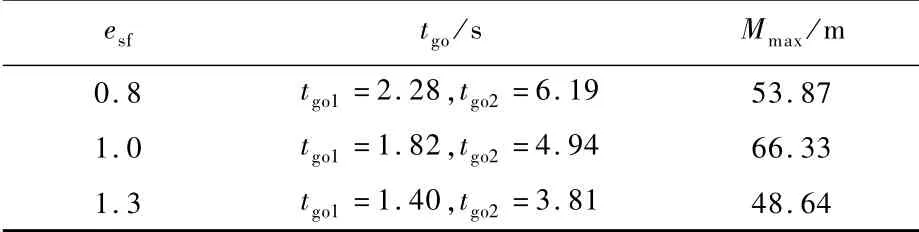
表4 标度系数误差变化时目标最优机动产生脱靶量（t f＝10 s）Table 4 Target optimal maneuver miss distance when scale factor error changes（t f＝10 s）

当估计剩余飞行时间存在零偏误差时，选择eb的变化范围为［－0.6，0.8］，飞行总时间为tf＝1 0 s，得到目标做最优机动时，各误差系数对应的导弹脱靶量，如图12所示。选取eb为－0.3，0.7，仿真总飞行时间在［0，10］s变化，得到目标最优机动产生的脱靶量如图13所示；最优控制切换时刻取值和tf＝10 s时对应脱靶量如表5所示。

图10和图12，分别给出了总飞行时间一定，目标采用最优机动突防策略产生的脱靶量关于标度系数误差esf和零偏误差eb的曲线。可以看出，估计剩余飞行时间中，这2个误差的存在都会使目标机动突防性能下降，当tgo准确时，最优机动突防产生脱靶量达到66.33 m，而当esf＝1.4或eb＝0.8时，脱靶量都接近于40m；当误差系数在esf＝1或eb＝0（即不存在误差的情况）附 近小范围变化时，对最终脱靶量的结果影响较小，误差尚可接受。

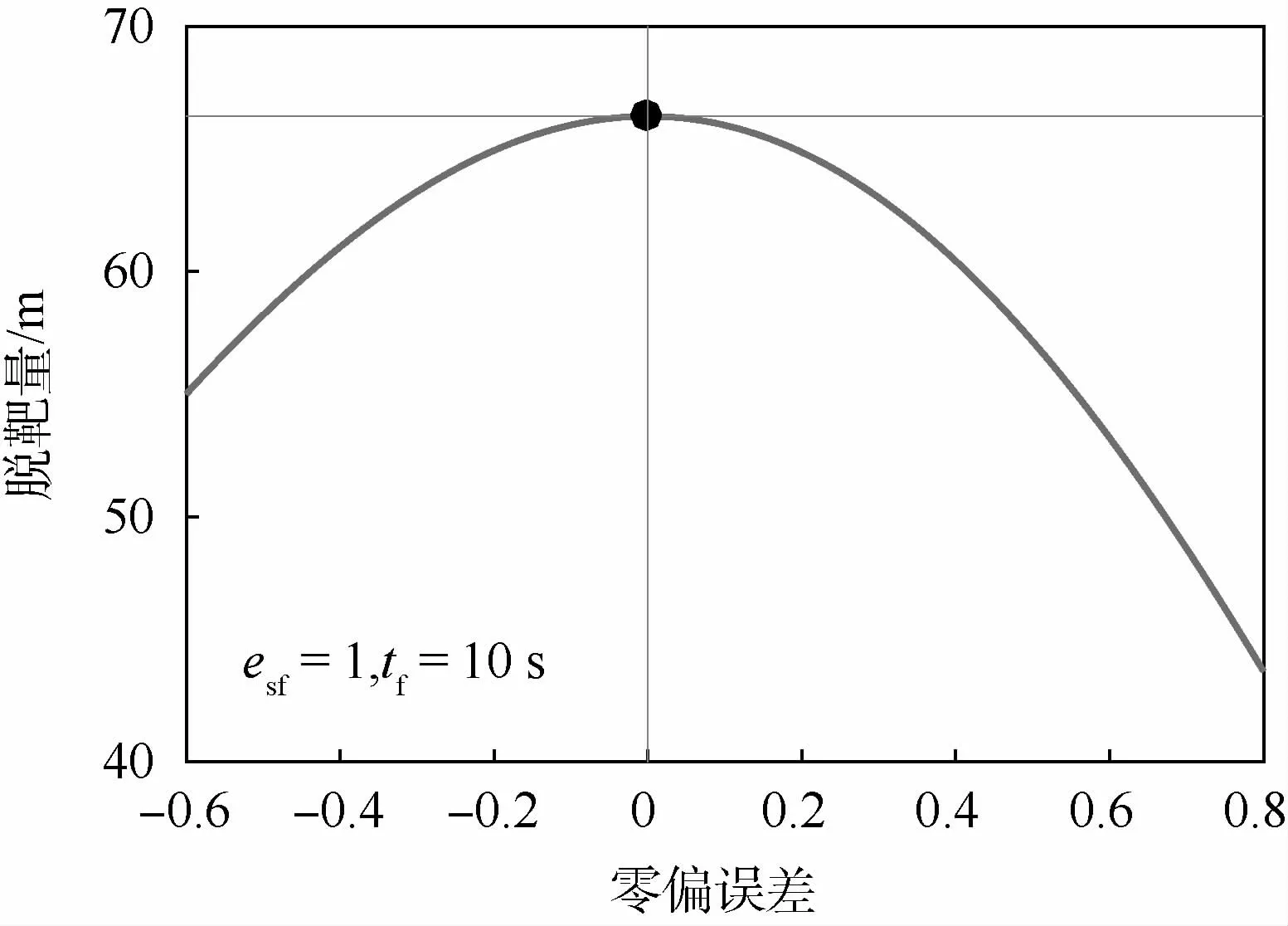
图12 目标最优机动脱靶量关于剩余飞行时间零偏误差的曲线Fig.12 Curve of target optimal maneuver miss distance relative to bias error of time to go

图13 零偏误差存在时目标最优机动产生脱靶量Fig.13 Target optimal maneuver miss distance when bias error exists

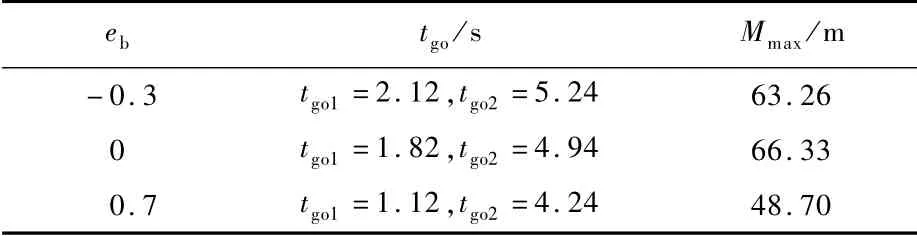
表5 零偏误差变化时目标最优机动产生脱靶量（t f＝10 s）Table 5 Target optimal maneuver miss distance when bias error changes（t f＝10 s）

图11、图13以及表4、表5，给出了存在不同剩余飞行时间估计误差下，目标最优机动突防引起的脱靶量关于总飞行时间的曲线。当估计剩余飞行时间的标度系数误差esf和零偏误差eb存在时，得到的脱靶量都要小于最优机动情形（无估计剩余飞行时间误差）。原因在于这些估计误差将会导致bang-bang控制切换时间发生变化，得到的bang-bang机动并不是最优的。将剩余飞行时间存在估计误差与目标做蛇形机动的情况对比，发现一般误差存在下，最优机动的脱靶量还总是大于蛇形机动的；但误差较大时（例如esf＝1.3或eb＝0.7），蛇形机动在某些总飞行时间下（例如2、5、8 s附近）的突防效果反而更佳。故针对误差存在时，削弱最优机动突防效果情况的出现，一方面，目标需要提高其上如导引头等探测装置的探测精度；另一方面，如存在无法克服的探测误差且数值较大时，可适当选择不需要剩余飞行时间信息的蛇形机动作为机动突防形式。

4 结 论

本文研究了拦截弹为比例导引制导时，目标最优机动突防策略及其影响因素的问题：

1）拦截弹的制导系统为一般线性高阶时，基于脱靶量级数解公式进行仿真分析，提高了计算效率，且实用性、通用性更强。

2）目标最优机动突防效果受导弹模型准确性影响。导弹制导系统为高阶时，目标最优机动产生脱靶量较大，突防成功百分比高；当制导系统传递函数形式更复杂时，脱靶量反而较小，说明真实拦截弹模型对目标的威胁性更大。导弹模型选为线性时，仿真较非线性结果吻合度较高，模型选取合适。

3）目标最优机动控制切换次数和切换时刻受拦截弹有效导引比N影响，且主要取决于剩余飞行时间tgo。目标最优机动突防效果对有效导引比估计误差不十分敏感，对剩余飞行时间估计误差较为敏感且随着误差增大目标突防性能大幅下降。

4）目标最优机动突防效果优于同等仿真条件下的一次阶跃机动、蛇形机动。但在总飞行时间较小时，阶跃机动突防性能与最优机动基本无差；在存在剩余飞行时间估计误差时，蛇形机动要优于某些最优机动。因此，目标可根据实际作战情况选择合适的机动策略，实现最佳突防。

作者简介：

王亚帆 女，硕士研究生。主要研究方向：导弹制导与控制。

周韬 男，硕士，副教授，硕士生导师。主要研究方向：导弹总体设计与仿真、导弹制导与控制。

陈万春 男，博士，教授，博士生导师。主要研究方向：飞行力学、导弹制导与控制。

Optimal maneuver penetration strategy based on power series solution of miss distance

WANG Yafan，ZHOU Tao，CHEN Wanchun*，HE Tailong
（School of Astronautics，Beihang University，Beijing 100083，China）

Abstract：Aimed at the proportional guidance missile，the state space model of high-order guidance system was established，and the optimal maneuver penetration strategy and influencing factors were studied based on power series solution of miss distance.First，when the missile guidance system was linear first-order and high-order，the simulations of optimal target maneuver penetration were carried out.The results show that the accuracy of the missile guidance model has an impact on the penetration effect，and the high order has larger miss distance and is more realistic.Then，the results were compared with step maneuver and weaving maneuver，the optimal maneuver penetration effect is the best.Furthermore，a two-dimensional nonlinear missile-target engagement model was established，and the simulation shows that the miss distance curve of optimal maneuver is highly identical with the linear system，and the linear system is selected appropriately.Finally，the impacts of effective navigation ratio and time-to-go estimation error on the optimal maneuver penetration effect were studied.The effective navigation ratio estimation error has little effect on the optimal maneuver penetration effect，the time-to-go estimation error makes the target optimal maneuver penetration performance decline greatly，and in some cases it is even worse than the weaving maneuver penetration effect.

Key words：penetration；optimal maneuver；power series solution of miss distance；estimation error；adjoint method；simulation analysis

Received：2019-04-01；

Accepted：2019-08-30；

Published on line：2019-09-12 15：51

URL：kns.cnki.net／kcms／detail／11.2625.V.20190912.1514.001.html

*Corresponding author.E-mail：wanchun＿chen