深度学习机制与小波融合的超分辨率重建算法

杨思晨，王华锋，王月海，李锦涛，王赟豪

（1.北方工业大学 信息学院，北京100144； 2.北京航空航天大学 软件学院，北京100083）

随着数字图像处理技术的不断发展，人们对于图像质量的要求越来越高。在实际应用中，高分辨率图像中具有更多的细节信息，更有利于处理和分析。但是，受成像设备质量的制约，生成的图像通常都不能满足人们的需求。提升图像的清晰度并得到高分辨率图像的一种直接有效的方法是增强图像成像系统的硬件质量，但这种方法不仅复杂度高，而且成本昂贵［1］。因此，作为一种通过计算机对低分辨率图像进行处理从而重建出高分辨率图像的图像处理技术，超分辨率重建技术成为了图像处理领域的研究热点。

超分辨率重建技术广泛应用于医学成像、卫星影像、航空遥感、刑事侦查等多种领域。在医学成像［2］中，运用超分辨率重建技术可以帮助医生进行更准确的医疗诊断；在卫星影像［3］和航空遥感［4］检测时，运用超分辨率重建技术可以获取更多复杂的地理环境细节；在刑事侦查领域［5］，超分辨率重建技术可以帮助提供更准确的嫌疑人信息，为侦查过程提供便利。

超分辨率重建算法可大致归结成3类：基于插值、基于重建模型和基于学习［6］。基于插值的算法［7-9］是通过低分辨率图像已知像素进而估计放大后高分辨率图像的未知像素。基于重建模型的算法［10-12］是将低分辨率图像作为约束的前提下，结合图像的先验知识进行图像重建。基于学习的算法［13-17］则是通过学习高分辨率图像和低分辨率图像的特征之间的映射关系实现图像的重建。相比于基于插值、基于重建模型这2类算法，基于学习算法重建的图像无论在准确性还是在视觉效果方面都存在优势。其中，基于深度学习的超分辨率重建算法的效果尤其突出。

基于深度学习的超分辨率重建算法是近几年迅速发展起来的，并获得了相比于传统方法准确度和清晰度更高的重建结果。但是，部分基于深度学习的超分辨率重建算法将最小化均方误差作为优化目标［14-16］。这种算法虽然可以提升重建图像的客观评价指标，但却不能有效重建出图像的细节纹理。2017年，Ledig等［18］提出基于生成对抗网路的超分辨率重建算法（Super-Resolution using a Generative Adversarial Network，SRGAN），将生成对抗网络应用到超分辨率重建领域，并重建出边缘纹理较为清晰的高分辨率图像。

为了重建出更真实的图像细节信息，本文从提升低分辨率图像中缺少图像的高频细节信息角度出发，提出一种融合了小波变换技术和生成对抗网络技术的超分辨率重建算法。首先，将小波分解与重构过程变换到由生成网络结构中的卷积层和反卷积层来完成，使分解的小波系数在并行的独立子网中进行训练；然后，通过反卷积的方式再将子网的输出合并为重建图像；最后，利用判别网络来鉴别生成网络输出的图像是否为高分辨率图像。这种算法发挥了小波变换和生成对抗网络在超分辨率领域的优势，使重建图像具有较好的纹理信息，在视觉上更加清晰。本文的主要贡献如下：①将小波变换技术与生成对抗网络模型融合，设计新的网络模型。小波主要在生成模型中通过卷积层将前一层卷积输出的特征图像进行小波分解，分解的图像在独立的子网中再进行特征的提取。这样做有利于网络全面地了解到图像不同频率的信息，使重建图像更加清晰。②提出一种融合小波系数损失的感知损失函数。感知损失函数考虑到人的视觉感知，可以得到视觉上清晰的超分辨率重建结果。③为了可以更准确地评价重建图像的质量，提出利用局部二值模式（Local Binary Patterns，LBP）提取重建图像特征，根据与原始图像特征分布的比较评判图像的纹理复原度。

1 相关工作

1.1 基于深度学习的图像超分辨率重建

近几年，基于深度学习的超分辨率重建算法发展迅速，并获得了相比于传统方法准确度和清晰度更高的重建结果［14-17］。基于深度学习的算法主要是通过学习高分辨率图像和低分辨率图像特征之间的非线性映射实现图像的重建。2014年，Dong等［14］提出一种基于卷积神经网络的超分辨率重建算法，这种算法虽然仅具有3个卷积层，却得到了比传统方法精确度更高的结果。受Dong等［14］影响，Kim等［15］提出一种网络深度和精度都进一步提升的递归网络结构，并同时解决了在网络深度增加导致的网络中不同参数的数量增加的问题。文献［16］引入一种亚像素卷积结构并采用直接在低分辨率图像尺寸上提取特征计算得到高分辨率图像方法，有效提升网络的运行效率。文献［17］引入了Desent Block结构，这种结构将前一层网络训练出的特征值传递到下一层网络，这样可以减轻梯度消失问题、减少参数数量。2017年，Lai等［19］提出一种级联的网络结构，每一级都只对原图放大2倍，之后通过一个残差网络得到每级的结果。

为了重建出图像的纹理细节，使重建图像在视觉上更加清晰，Ledig等［18］通过改进生成对抗网络模型的结构并利用感知损失函数重建出边缘纹理较为清晰的结果。然而经实验验证，这种仅依赖于传统的生成对抗网络模型重建的图像虽然视觉上清晰，但测试出的客观评价指标相对较低，而且重建图像经过局部放大后，边缘纹理与原始图像并不相近。为了使生成对抗网络可以有效地重建出更自然的纹理信息，本文提出通过在生成对抗网络中应用小波变换技术实现对小波系数进行训练的一种融合小波变换以及生成对抗网络的超分辨率重建算法。实验证明，本文算法可以重建出细节更加清晰的图像。

1.2 基于小波变换的图像超分辨率重建

图像的小波变换是对图像在频率空间做分解。根据小波变换的原理，图像在经过二维离散小波分解后可以得到近似系数以及水平、垂直、对角3个方向的细节系数共4个小波分量。在超分辨重建中，将小波变换应用到神经网络里，可以使网络既能了解到图像的整体，又可以分析图像的局部细节，达到对图像有多方面、更深入的认识的作用，从而可以获得精确率更高、细节上更加接近于原始高分辨率图像的重建结果。

目前，小波变换已经成功应用到超分辨率重建领域。2008年，电子科技大学的Guo和He［20］将小波变换技术应用到凸集投影法（Projection onto Convex Sets，POCS）中，小波变换在做图像重建时不仅抑制了噪声又保留图像中原有的低频信息，重建结果比POCS算法的准确度更高。Akbarzadeh等［21］指出使用双三次插值和平稳小波变换实现图像的重建的图像比其他传统算法更加清晰。Kumar等［22］提出将低分辨率图像视为小波分解后的近似系数，用来估计图像中的细节系数。Huang等［23］提出一种结合小波变换与卷积神经网络的网络结构，在该算法中，网络模型通过学习图像小波分解系数的映射关系实现高分辨率图像的重建，并重建出较好的图像边缘细节。

受Huang等［23］的影响，本文将小波变换技术与生成对抗网络相融合，这样有利于使重建图像具有更加真实的细节纹理。

2 算 法

超分辨率重建的目标是通过一定的算法将低分辨率图像转换为高分辨率图像。而一般低分辨率图像中缺少细节信息，才导致其在视觉上有模糊感的，根据这一信息，本文提出一种可以有效重建图像局部细节信息的超分辨率重建算法。

本文提出的超分辨率重建算法结合了小波变换技术和生成对抗网络，利用生成对抗网络可以重建出纹理细节更加真实的图像的优势，并在网络中通过小波多分辨分析训练小波分解系数来提高网络在训练过程中对于图像局部细节的理解，最终可以重建出在图像高频细节和清晰度都更优的高分辨率图像。本节将详细介绍这种图像超分辨率重建算法的具体操作。

2.1 小波变换

在本文提出的算法中，网络训练时通过对图像小波分解系数的训练完成图像的超分辨率重建。在网络中，利用卷积层通道间的变化实现对特征图像的小波分解，分解的4个系数分别作为4个独立的子网的输入，最后通过一个反卷积层再将训练完的小波系数合并。子网间相互独立，互不影响。这种算法可以实现在生成对抗网络中对图像进行多分辨分析，可以使网络既能了解到图像的整体，又可以分析图像的图像细节，使网络对图像有多方面的认识和更加深入的理解，从而有效地重建出图像细节更加精确、更加接近于原始图像的训练结果。

在对图像进行小波变换时，将图像视为具有索引［m，n］的二维信号，则有IHR［m，n］表示位于第n列和第m行的像素值。二维信号IHR［m，n］可以被视为在给定的第n行IHR［m，：］之间以及给定的第m列IHR［：，n］中的一维信号。若输入的低分辨率图像为IHR［m，n］，设定小波变换中高通和低通滤波器分别为h［k］和l［k］，k表示小波的位置，K表示小波变换中平移操作所经过的距离。在二维离散小波变换过程中，首先对n方向做高通和低通滤波以及降频处理，得到

接着再沿m方向做高通和低通滤波以及降频处理：

另外，在进行二维图像的离散小波分解与重构时，常采用Haar小波函数作为小波基函数。Haar小波函数是最早的具有紧支撑的正交小波基函数，其函数简单、应用也最为广泛，尤其是其具有较好的对称性，在训练过程中应用Haar小波函数可以有效避免图像分解时产生相位失真。

2.2 生成对抗网络

在生成对抗网络中，需要定义一个生成网络G和一个判别网络D。生成对抗网络训练的过程就是生成网络和判别网络的不断交替优化的过程，优化过程可以定义为

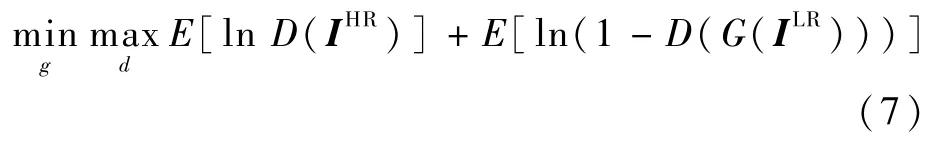
式中：g和d分别为生成网络和判别网络中的网络参数；E表示求均值。

通过这种算法，生成网络可以不断优化并得到与原始图像极为相似的输出结果。因此，基于生成对抗网络的图像超分辨率重建可以得到视觉效果好的重建图像。

在改进的生成对抗网络中，生成网络主要分为2个过程（见图1）：第1个过程主要是将低分辨率图像通过卷积表示为特征图；第2个过程是将特征图分解为小波系数来估计高分辨率图像的小波系数，并在最后利用反卷积层将估计的小波系数合并为重建图像。而在生成网络中最重要的部分是具有相同结构的残差块，残差块的作用主要是有效处理网络深度较深的网络，可以降低生成对抗网络的训练难度。原始残差网络［24］结构中包含2个卷积层和2个批量标准化层以及激活函数Relu，如图2（a）所示。受Lim等［25］的启发，本文采用其提出的残差块结构，如图2（b）所示。具体来说，本文去除了结构中的标准化层，因为残差块中的标准化层在网络训练时会占用较大的内存，若将其从残差结构中去除，可以有效提升网络训练效率和性能［25］，并将激活函数用PRelu代替原来的Relu。

判别网络的作用是判断生成网络的输出是否为高分辨率图像，在网络结构上不做过多的修改，将采用Ledig等［18］提出的用于超分辨率重建的生成对抗网络结果中的判别网络模型，如图1中判别网络模型所示。

图1 生成对抗网络模型Fig.1 Generative adversarial network model

图2 残差网络模型Fig.2 Residual network model

2.3 损失函数

在神经网络中，训练过程是一个通过迭代不断降低损失值并得到最优解的过程。在超分辨率重建领域常用最小均方误差（Mean-Square Error，MSE）作为训练过程的损失函数，因为图像质量评估标准中峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）值与最小均方误差相关，所以均方误差作为损失函数时可以获得较高的PSNR值。但是，利用这种方法重建出的图像的边缘有明显的锯齿，视觉上觉得图像较为模糊。Ledig等［18］认为损失函数不仅要考虑评估标准更要考虑人的感知，其提出一种感知损失函数定义为内容损失lC和对抗损失lA的加权和，损失函数l可以表示为

式中：内容损失lC表示特征空间的最小均方误差，是图像通过19层的VGG19网络提取出的高层特征间的均方误差。利用图像高层特征间的误差函数作为网络的损失函数，可以有效提高重建图像中的纹理信息，使图像看起来更加清晰。

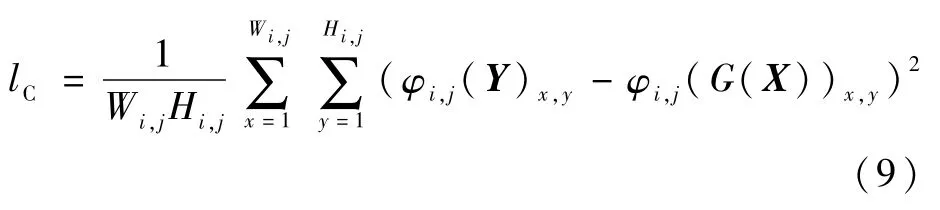
式中：φi，j为VGG19网络中第i层maxpooling后第j层卷积得到的特征图；Wi，j和Hi，j为VGG19网络中对应特征图的维数；X表示输入的低分辨率图像；Y表示原始高分辨率图像。

对抗损失lA是基于鉴别网络的输出的概率得出的，一般表示为

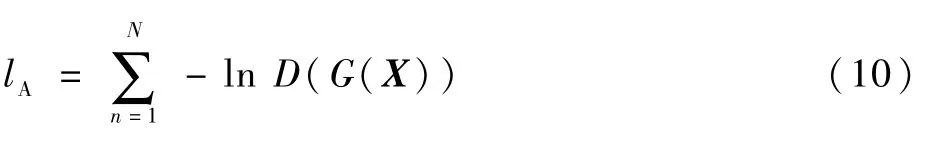
由于SRGAN［18］重建图像的纹理放大后过于不自然，为了处理这个问题，在生成对抗网络中增加小波变换的处理过程，让网络可以训练图像的小波分解系数，从而提高重建图像中的高频细节信息，使图像的纹理更加真实。因此，本文的损失函数l′是在SRGAN感知损失函数的基础上加入了小波系数的损失，l′可以表示为

式中：lW为小波分解系数的最小均方误差，可以表示为

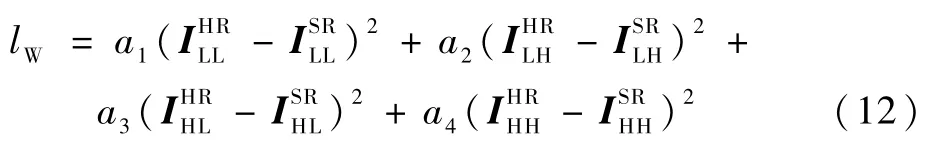
其中：a1～a4为权重系数为生成网络重建出的图像的小波分解系数。

3 实 验

3.1 数据准备

本文使用VOC2012数据集［26］作为改进的网络的训练集。同时，为了可以进行公平的比较，也用此数据集训练了SRGAN 网络［19］。VOC2012数据集是一组用于图像重建的高质量的图像数据集，其中包括16 700张训练图像和425张测试图像。VOC2012数据集中具有20类图像，种类丰富，利于图像的超分辨率重建。但是又不像ImageNet数据集［27］拥有大量的图像数据，增加生成对抗网络的训练难度。测试时，使用标准数据集Set5数据集［28］、Set14数据集［29］和BSD100数据集［30］对训练的网络进行测试。

3.2 评价标准

现在超分辨率重建领域最为常用的评价重建图像质量的指标为PSNR和结构相似性（Structural Similarity index，SSIM）［31］。不过许多研究都表明均方误差和PSNR并不能准确反映图像的视觉质量，所以还引用了特征相似度（Feature Similarity，FSIM）［32］、通 用 图 像 质 量（Universal Image Quality，UIQ）［33］和LBP［34］来评价重建图像质量。

根据人类视觉系统（Human Visual System，HVS）主要通过图像的低级特征来理解图像，Zhang等［32］提出了FSIM。相位一致性可以提取高度图像信息特征，但不能响应图像对比度的变化，因此引入梯度特征来提取对比度信息。相位一致性用作FSIM 的主要特征，梯度用作次要特征。FSIM值越大，就表示图像之间的FSIM越高，重建图像的质量越好。若有p表示图像像素点，则FSIM的表达式为

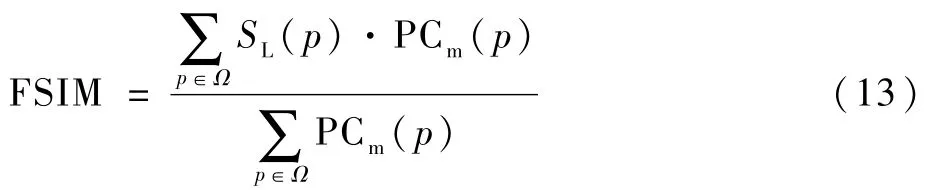
式中：Ω为整个图像的像素域；SL（p）和PCm（p）的表达式分别为

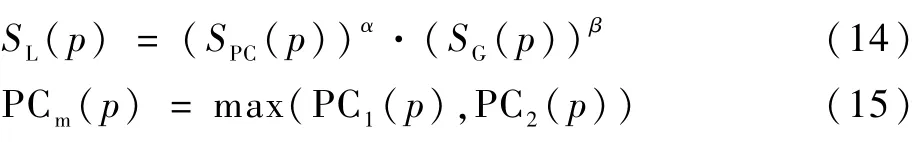
其中：SPC（p）和SG（p）分别为图像的相位一致性和梯度幅度；α和β为用于调整相位一致性和梯度幅度重要性的参数，取值均为1。

UIQ是一种结合了线性相关损耗、亮度失真和对比度失真3个因素的图像质量评估指标。UIQ值越大，表示重建图像与原始图像在线性、亮度和对比度3个方面的相关度越高，重建图像质量越好。根据Wang和Bovik［33］，定义w为重建图像，y为原始高分辨率图像，则UIQ的表达式为

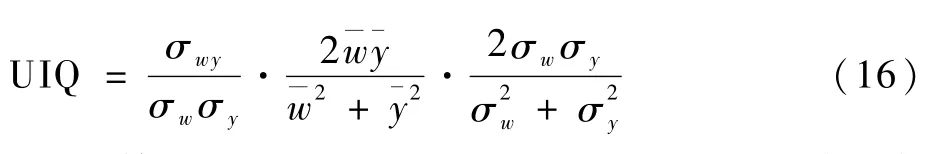
式中：第1项表示w和y之间的线性相关系数，当值为1时表示w和y线性相关；第2项表示图像亮度的相关性；第3项表示图像对比度的相关性；w和y分别表示输出结果与原始图像；σw、σy分别为w和y的标准差；σwy为w、y的协方差。

LBP是一种提取图像纹理特征的算法。以一个3×3的图像局部窗口为例，若这个窗口的中心坐标为（x，y），且像素值为I，则根据其周围的8个坐标的像素值大小定义LBP码，如果周围坐标的像素值大于中心坐标则记为1，否则记为0。这样就可以得到8位二进制码，将其转化为十进制则为LBP值。具体计算过程如下：

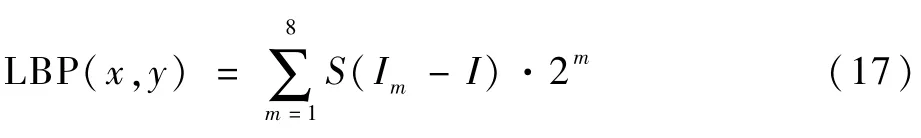
式中：Im为中心坐标周围8个坐标的像素值。若有i表示坐标像素值的差，S函数式为

LBP方法是一种高效的特征分析方法，该方法运算速度快，具有灰度不变性和对光照变换不敏感的特点。

3.3 训练过程

本文使用VOC2012数据集［24］中16 700张训练样本在NVIDIA Titan X GPU上利用TensorFlow平台对本文提出的网络进行了训练。训练时间大约需要5天。

低分辨率图像是对16 700张高分辨率图像进行降采样因子为4的双三次插值处理得到的。训练时，将高分辨率图像随机剪成大小88×88的子图像，网络通过学习低分辨率图像与高分辨率图像的小波分解系数之间的映射关系实现图像重建。将网络中批尺寸的大小设置为16，网络以0.000 2学习率进行训练，总共进行313 200次迭代。使用感知损失函数训练网络，这样可以得到视觉效果更好的结果。

3.4 定量评估

为了显示本文算法的性能，将本文算法与SRGAN算法进行定量的比较，利用Set5和Set14数据集对2种方法进行测试，得到的放大倍数为4的重建图像的PSNR和SSIM 结果如表1所示。本文利用VOC2012训练集重新对SRGAN进行训练，因此得到的SRGAN的测试结果与原文中的测试结果略有差异。从表1中可以发现，本文算法的图像质量评估标准PSNR和SSIM 相比于SRGAN有明显的提升，最少分别提高了0.99 dB和0.031。为了可以更加准确地评价重建图像质量，使用了FSIM 和UIQ进一步分析实验结果。从表2可以看出，本文算法在FSIM 和UIQ评估指标中都取得了良好的效果。

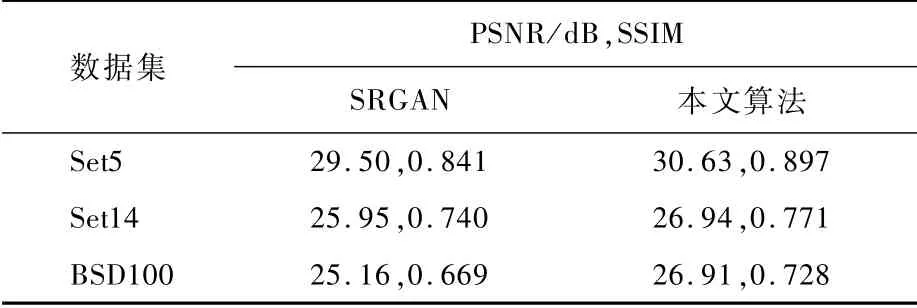
表1 PSNR和SSIM 的测试结果Table 1 Test results of PSNR and SSIM

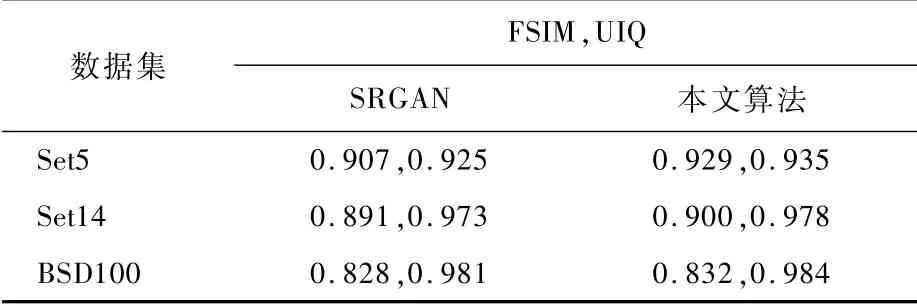
表2 FSIM 和UIQ的测试结果Table 2 Test results of FSIM and UIQ

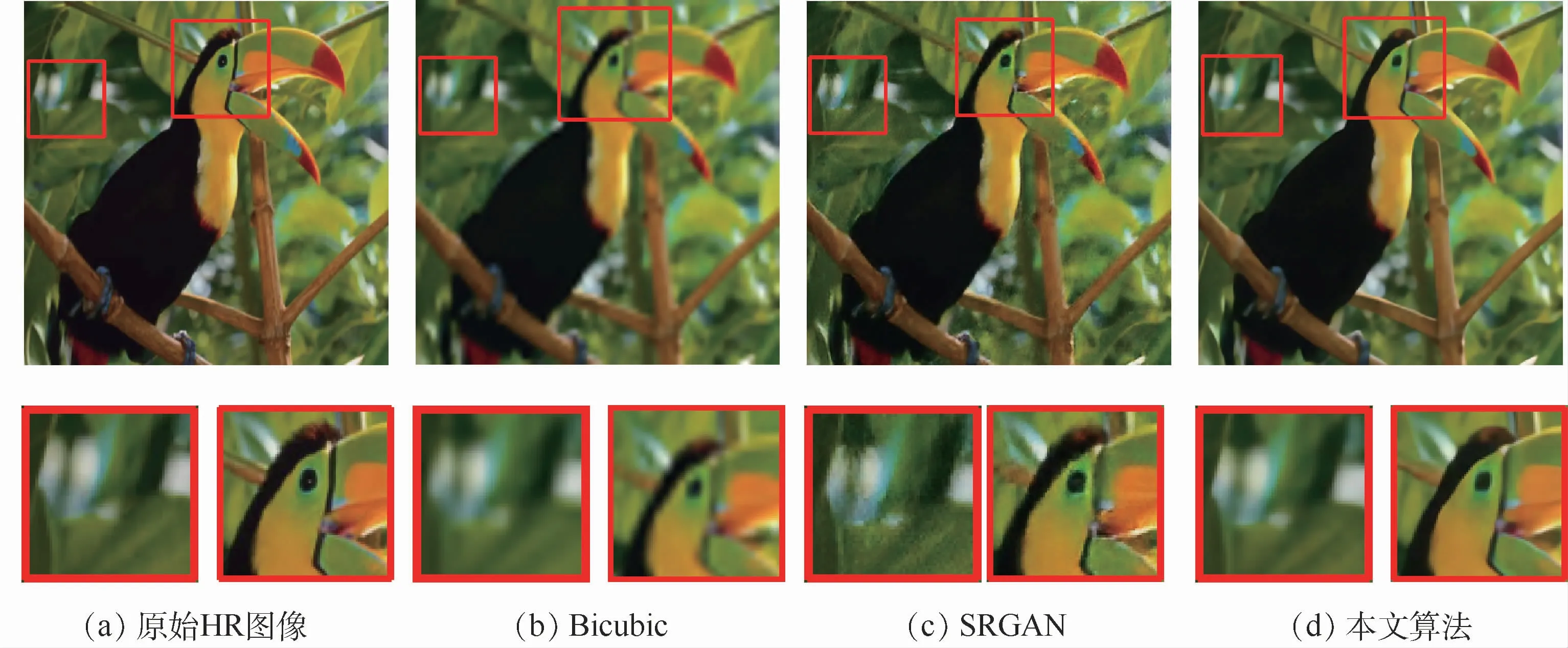
图3 Set5数据集中图像“bird”测试结果Fig.3 Test results of“bird”image in Set5 dataset

图4 Set14数据集中图像“barbara”测试结果Fig.4 Test results of“barbara”image in Set14 dataset

图3～图5分别为Set5数据集中的图像“bird”、Set14数据集中的图像“barbara”和图像的测试结果。其中图3（b）、图4（b）和图5（b）为传统的双三次插值算法（Bicubic）的重建结果，仅仅是对图像进行了4倍的上采样，图像边缘模糊感明显。图3（c）、图4（c）和图5（c）为SRGAN算法的重建结果，图像复原出边缘细节信息且看起来比较清晰，但局部放大后“伪纹理”相对明显。图3（d）、图4（d）和图5（d）为本文算法的重建结果，相比于SRGAN算法放大后的“伪纹理”没有了，看起来边缘的纹理细节比较平滑，更加清晰。从结果中可以发现，本文算法不仅在一定程度上提升了客观评价指标，而且改善了SRGAN中图像纹理不自然的问题。本文的重建结果边缘细节更加清晰，纹理更加真实，视觉质量上也更优，充分展示了小波变换与生成对抗网络的优势。

应用LBP测试图像是为了更好地观测重建图像纹理特征复原度。LBP是一种可以有效提取和描述图像的纹理细节和特征结构的算子。本文利用LBP对重建图像的纹理特征进行提取，并获取相关描述图像特征的分布图。

图5 Set14数据集中图像“monarch”测试结果Fig.5 Test results of“monarch”image in Set14 dataset

图6 重建图像的LBP特征分布Fig.6 LBP feature distribution of reconstructed image

图6为图3～图5中SRGAN算法及本文算法的重建图像的LBP提取的特征分布。其中，图6（a）、（b）和（c）为SRGAN算法重建图像的LBP特征分布图，图6（d）、（e）和（f）为本文算法重建图像的LBP提取的特征分布图。从图中可以发现，相比于SRGAN算法，本文算法的LBP直方图曲线跟原始高分辨率图像LBP直方图曲线重合率更高，也就表示本文算法的重建图像在图像的纹理特征层面要比SRGAN算法相对较好。为了更好地展现本文算法重建图像的纹理特征与原始图像更相近，计算了重建图像与原始高分辨率图像LBP提取的特征图之间的方差，如表3所示。显然，本文算法的方差要比SRGAN算法低，进一步说明融合小波变换的生成对抗网络模型超分辨率重建算法存在优势。

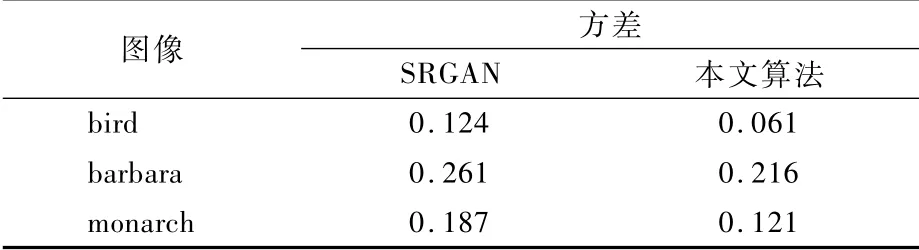
表3 重建图像LBP特征图与原始图像LBP特征图之间方差Table 3 Variance between LBP feature map of reconstructed im age and LBP feature map of original image

4 结 论

1）为了进一步提升重建图像质量，本文提出将小波变换融合到生成对抗网络结构中。将小波分解与重构过程变换到由生成网络结构中的卷积层和反卷积层来完成，实现网络对图像的小波分解系数的训练，并在单独的子网中进行互不影响的训练。通过一系列的实验验证，本文提出的超分辨率重建算法可以有效提升PSNR、SSIM、FSIM 和UIQ的值，同时又生成了纹理细节较为真实的重建图像。体现了本文算法在超分辨率重建领域的优势。

2）提出一种加入了小波分解系数损失的感知损失函数。因为感知损失函数考虑了人的视觉感知，可以重建出纹理较清晰的图像。因此，本文在SRGAN算法中提出的感知损失函数的基础上增加了小波系数的损失。

3）在利用本文算法进行超分辨率重建的图像中存在一些在处理过程中引入的噪点，并且有少量结果的噪点较多，直接影响了图像的视觉质量。可能致使这些噪点产生的原因是：对于尺寸较小的图像，网络训练小波系数过于强调图像的边缘细节而产生了图像噪声。之后可以考虑进一步的改进，去除重建图像中的噪点，提升算法的重建结果的精确度。