混凝土与各向同性岩石强度理论研究进展
2020-02-10丁发兴余志武龚琛杰
丁发兴,吴 霞,向 平,余志武,龚琛杰
(1.中南大学土木工程学院,湖南,长沙 410075;2.湖南省装配式建筑工程技术研究中心,湖南,长沙 410075)
混凝土(包括轻骨料混凝土)和岩石两大类土木工程材料在各类工程与自然界中广泛应用或存在,它们大多处于复杂受力状态。两大类土木工程材料强度理论是工程结构强度与围岩稳定性分析等的基础理论,在现代建筑、水利与交通等工程中具有重要应用意义。近年来随着强度理论的逐渐发展与成熟,其中混凝土结构设计率先挖掘其塑性潜能。
古典强度理论对于材料破坏的原因有明确的理论观点,概念明确,表达式简单,参数少且易于确定,但难以准确反映复杂应力状态下两大类土木工程材料的强度变化规律。18世纪Coulomb[1]提出了适用于砂土的强度理论,此后引领了众多学者对各类土木工程材料强度理论的研究热情。Mohr-Coulomb强度理论[2]建立的砂土强度理论得到各界广泛认可并大量应用,至今已有上百种基于各向同性假设的强度理论,该类强度理论可分为剪应力强度理论、八面体强度理论与主应力强度理论。剪应力强度理论与主应力强度理论基于材料破坏的力学观点与力学模型而提出具有一定物理意义的强度理论,剪应力强度理论包括单剪和双剪两个系列强度理论,主应力强度理论主要是Mises屈服理论和损伤比强度理论,而八面体强度理论基于大量试验数据而对材料破坏包络面进行数学拟合,或根据材料破坏面几何形状特征给出数学表达式而对其中参数进行拟合。
目前,土木工程材料强度试验资料丰富,理论研究成果也丰富,本文在现有混凝土与各向同性岩石三轴试验资料的基础上,为保持工作的完整性首先对古典强度理论进行简单介绍,然后,结合收集到的试验资料对混凝土与各向同性岩石的主要现代强度理论进行比较、论述与总结,在此基础上对主应力空间损伤比强度理论进行展望。
1 古典强度理论
现有研究表明古典强度理论难以准确反映复杂应力状态下混凝土与各向同性岩石的强度变化规律,古典强度理论主要包括以下四大强度理论[1]:
1)第一强度理论,又称为最大拉应力理论(Rankine,1876年)[3],该理论适用于脆性材料,仅考虑最大主拉应力对材料破坏的影响,认为材料承受的最大主拉应力达到某一极限值时即发生破坏;
2)第二强度理论,又称为最大拉应变理论(Mariotte,1682年)[3],该理论适用于脆性材料,认为材料所承受的最大主拉应变达到某一极限值时发生破坏;
3)第三强度理论,又称为最大剪应力理论(Tresca,1864年)[3],该理论适用于低碳钢等塑性材料,认为材料所承受的最大剪应力达到某一极限值时发生塑性流动破坏;
4)第四强度理论,即 Mises屈服理论(Von Mises,1913年)[3],既称为主应力理论又称为八面体剪应力理论,该理论适用于塑性材料,认为材料所承受的统计平均剪应力或八面体剪应力达到某一极限值时屈服。
2 现代强度理论
为方便论述与比较,本文所有涉及强度理论的表达式,应力值统一规定受拉为正、受压为负,拉压子午线定义统一以θ= 0°时为拉子午线,θ= 60°时为压子午线;八面体强度理论各准则参数取值方法为数据拟合时,统一用笔者收集的各文献中拉、压子午线上实验数据对该准则的参数进行拟合而确定;双剪强度理论体系中,反映中间主切应力以及相应面上正应力对材料破坏程度的参数b统一取为1;强度理论中各符号的物理意义解释见附录。
2.1 混凝土强度理论
迄今为止众多国内外学者开展了混凝土多轴强度试验,根据国内外混凝土多轴强度的大量试验结果,混凝土破坏包络面的几何形状具有如下特征[3-5]:1)曲面连续、光滑、外凸;2)对静水应力轴三折对称;3)在静水应力轴的拉端封闭,顶点为三轴等拉应力状态;压端开口,不与静水压力轴相交;4)子午线上各点的偏应力或八面体剪应力值,随静水应力或八面体正应力的代数值的减小而单调增大,但斜率渐减,有极限值;5)偏平面的封闭曲线三折对称,其形状随静水应力或八面体正应力值的减小,由近似三角形逐渐外凸饱满,过渡为一圆。
国内外学者们提出的各种混凝土强度理论,先后出现八面体强度理论、双剪强度理论和主应力空间损伤比强度理论,各种理论[6-27]及其评述列表见表1,由表1可知:
1)混凝土八面体强度理论参数确定方法主要有应力特征点和最小二乘法,前者参数确定简便而后者需根据大量数据拟合参数,大多数八面体强度理论的三维破坏包络面顶点处出现尖角;
2)俞茂宏提出的双剪强度理论[3]考虑了作用于双剪单元体上的全部应力分量及其对材料破坏的不同影响方式,认为当作用于双剪单元体上的两个较大切应力及其相应面上的正应力影响函数到达某一极限时材料破坏,双剪强度理论体系中,两参数和三参数双剪强度理论[17,19]的破坏包络面由6或12个平面相交组成,四参数和五参数由6或12个曲面相交组成,相交处都不光滑,且顶点有尖角;
3)丁发兴和余志武[26―27]提出的主应力空间混凝土双参数损伤泊松比(简称损伤比)强度理论,将混凝土受压损伤比(vD,c>0.5,体积膨胀)和受拉损伤比(vD,t<0.5,体积收缩)作为强度准则的基本参数,受压损伤比考虑了Lode角的影响而受拉损伤比为一常数。
为了比较各准则的破坏包络面规律,笔者收集了国内外共397组混凝土多轴试验数据[28―37],各准则对应的拉压子午线与试验数据的比较如图1所示。图1中各准则中的参数取值方法为特征应力点法时,采用过镇海[3]建议的强度特征值,即单轴抗压强度fc、单轴抗拉强度ft= 0.1fc、二轴等压强度fcc= 1.28fc、三轴等拉强度fttt= 0.9ft、高静水压情况下σ8/fc=-4,τ8/fc= 2.7,θ= 60°,准则中只有 3个或4个参数选前3个或前4个特征强度,若准则已有规定的特征值或参数则取原值,准则参数取值方法为数据拟合的各参数取值见表1,由图1可见:

表1 各混凝土强度理论表达式Table 1 Expressions of concrete strength theory
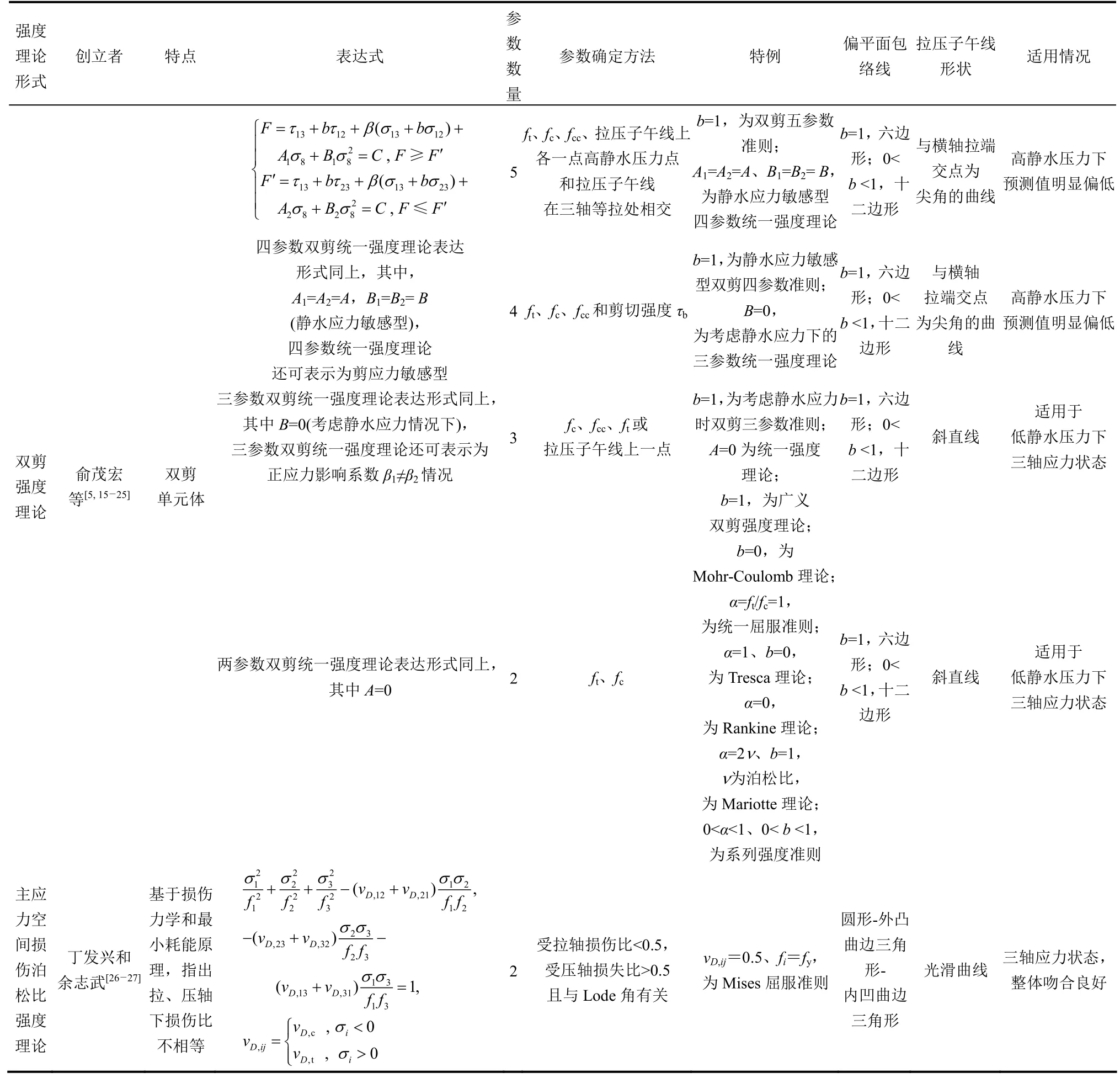
(续表)
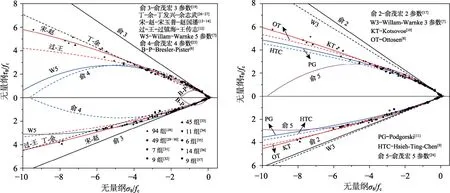
图1 各混凝土强度准则对应的拉压子午线比较Fig.1 Comparisons of concrete strength criterion between tensile and compressive meridian and experimental data
1)混凝土八面体强度理论中 Ottosen[8]、Kotsovos[10]以及宋玉普-赵国藩准则[13-14]等八面体强度理论与混凝土拉压子午线上的三轴试验数据变化规律较一致,其中 Kotsovos准则和宋玉普-赵国藩准则中的参数由数据拟合而定;
2)当静水应力σ8/fc>-4时,四、五参数双剪强度理论[23―24]与混凝土拉压子午线上的三轴试验数据变化规律较一致;
3)丁发兴和余志武[26―27]提出的主应力空间混凝土双参数损伤比强度理论,其三轴破坏面光滑连续,由于受压损伤比仅考虑了 Lode角而忽略了静水应力的影响,与试验结果相比,该准则在混凝土处于较高静水压力状态时略偏大,而在较低静水压力状态时略偏小。
由于各准则数量较多,选取在静水应力σ8/fc>-4时与混凝土拉压子午线上的三轴试验数据变化规律较一致的强度准则,该类准则对应偏平面图与试验数据的比较如图2所示,可见各准则的偏平面变化规律基本一致,其中两参数双剪强度理论[17]的破坏包络面基本上处于外凸八面体强度理论的外边界[38]。
混凝土各准则与试验数据八面体剪应力比较的均值和离散系数见表2,由于混凝土三轴破坏包络面上的试验数据点分布并不匀称,使得丁发兴-余志武[26―27]损伤比强度理论与试验结果相比精度最高,Hsieh-Ting-Chen[9]八面体强度理论次之,两者的离散系数相对最小。
2.2 轻骨料混凝土强度理论
根据国内外已有的轻骨料混凝土多轴强度试验结果,轻骨料混凝土破坏包络面的几何形状具有如下特征[3,39]:1)曲面连续、光滑、外凸;2)对静水应力轴三折对称;3)在静水应力轴的拉端和压端封闭,拉端顶点为三轴等拉应力状态,压端顶点为三轴等压应力状态;4)子午线上各点的偏应力或八面体剪应力值,随静水应力或八面体正应力的代数值的减小而增大,但斜率渐减,在中压应力区到达极限值,随即偏应力或八面体剪应力值,随静水应力或八面体正应力的代数值的减小而减小;5)偏平面的封闭曲线三折对称,其形状随静水应力或八面体正应力值的减小,由外凸曲边三角过渡为圆形。因此轻骨料混凝土的破坏面比混凝土破坏面要小,且与静水应力轴有两个交点。
国内外学者们提出的各种轻骨料混凝土强度理论,先后出现八面体强度理论与双剪强度理论,各种理论[39―44]及其评述列表见表3。
由表3可知:
1)与普通混凝土相比,已有轻骨料混凝土强度理论较少,并且以采用数学公式由试验数据进行参数拟合的八面体强度理论为主;
2)王立成和日和田·希与志[43]基于双剪强度理论体系的轻骨料混凝土五参数双剪强度理论的破坏面由6或12个曲面相交组成,相交处不光滑且顶点有尖角。
为了比较各准则的破坏包络面规律,笔者收集了国内外共97组轻骨料混凝土多轴试验数据[39-41],各准则对应的拉压子午线与试验数据的比较如图3所示。图3中各准则中的参数取值方法为特征应力点法时,采用准则已有规定的特征值或参数,准则参数取值方法为数据拟合的各参数取值见表3,由图3可见:
1)宋玉普-赵国藩[39]、王立成-宋玉普[40]、王万祯等[41]和叶艳霞-张志银[42]八面体强度理论中的参数都由数据拟合确定,与轻骨料混凝土拉压子午线上的三轴试验数据变化规律较一致,除叶艳霞-张志银[42]八面体强度理论的破坏包络面整体光滑连续外,其余理论破坏曲面都有尖角;
2)王立成-日和田·希与志五参数双剪强度理论[43]中参数由特征应力点法确定,与轻骨料混凝土拉压子午线上的三轴试验结果吻合度略差。
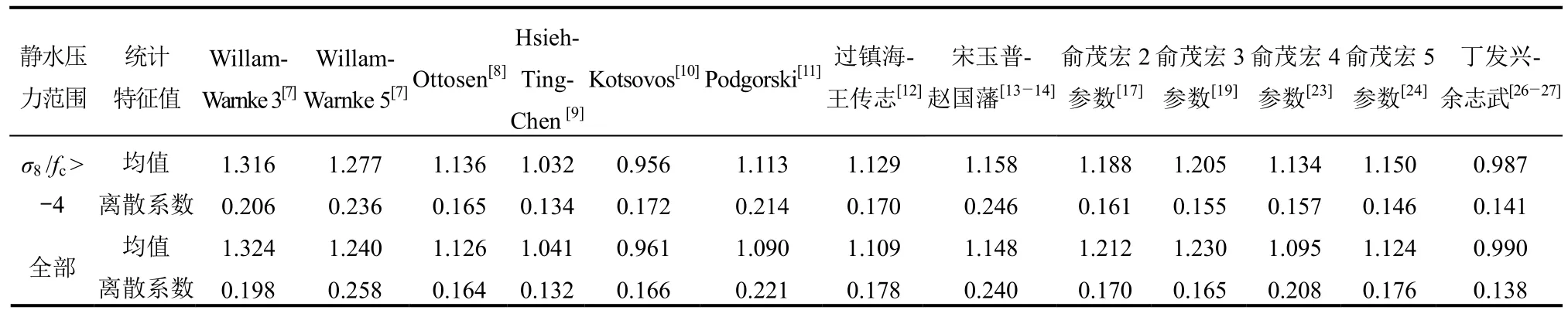
表2 各混凝土强度准则与试验数据比较统计表Table 2 Comparisons of concrete strength criterion by researches between predicted results and experimental data

表3 各轻骨料混凝土强度理论表达式Table 3 Expressions of lightweight aggregate concrete strength theory
各准则偏平面图与试验数据的比较见图4,各八面体强度理论的偏平面变化规律基本一致,王立成-日和田·希与志五参数双剪强度理论[43]的破坏包络面基本上处于外凸八面体强度理论的外边界。
轻骨料混凝土各准则与试验数据八面体剪应力比较的均值和离散系数见表4,由于轻骨料混凝土三轴破坏包络面上的试验数据点分布并不匀称,各准则离散系数都较大,相对而言,宋玉普-赵国藩[39]强度理论与试验结果相比均值最接近、离散系数相对最小。

图3 各轻骨料混凝土强度准则拉压子午线与试验数据比较Fig.3 Comparisons of lightweight aggregate concrete strength criterion between tensile and compressive meridian and experimental data
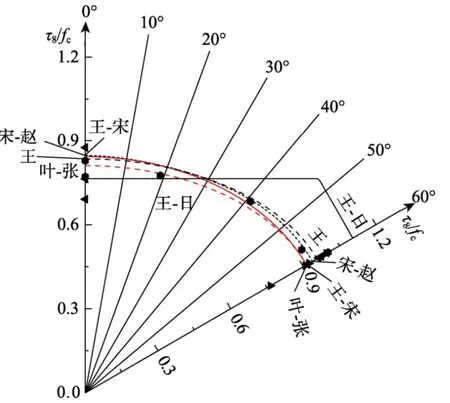
图4 各轻骨料混凝土强度准则对应的偏平面比较(σ8/fc = _1.5)Fig.4 Comparisons of lightweight aggregate concrete strength criterion between deviatoric plane and experimental data(σ8/fc =_1.5)

表4 各轻骨料混凝土强度准则与试验数据比较统计表Table 4 Comparisons of lightweight aggregate concrete strength criterion by researches between predicted results and experimental data
2.3 各向同性岩石强度理论
各向同性岩石材料与混凝土的破坏包络面的几何形状特征类似,并无明显差别,但其形成的破坏包络面比混凝土大,现有大多数各向同性岩石材料三轴破坏试验结果表明,单轴抗压强度大于100 MPa的岩石破坏包络面较大,而单轴抗压强度小于100 MPa的岩石破坏包络面次之。
目前,各向同性岩石强度理论主要采用Mohr-Coulomb强度理论[2]和 Hoek-Brown强度理论[45],而Drucker-Prager[46]准则大多应用于岩石数值计算。各向同性岩石强度理论先后出现单剪强度理论、八面体强度理论以及双剪强度理论,国内外各种强度理论[2,45―63]及其评述列表见表5,由表5可知:
1)Mohr-Coulomb单剪强度理论认为最大剪应力和相应剪切面上的正应力共同导致材料破坏,适用于单轴抗拉强度与单轴抗压强度不相等的脆性材料,其特征是未考虑中间主应力的影响,理论值偏低,该理论破坏包络面由6个平面相交,相交处不光滑且顶点有尖角;
2)岩石八面体强度理论参数的确定方法主要有应力特征点法、试验数据拟合以及由岩石软硬程度和破碎程度确定,大多数八面体强度理论的三维破坏包络面顶点出现尖角;
3)双剪强度理论体系中,两参数、三参数线性双剪强度理论[17,19]的破坏包络面由6或12个平面相交组成,三参数非线性双剪强度理论[61]的破坏包络面由6或12个曲面相交组成,相交处都不光滑且顶点有尖角。
为了比较各准则的破坏包络面规律,笔者收集了国内外共107组单轴抗压强度小于100 MPa的岩石(用“岩石Ⅰ类”表示)多轴试验数据[49,64-68]和116组单轴抗压强度大于100 MPa的岩石(用“岩石Ⅱ类”表示)多轴试验数据[48,69―70],岩石强度理论的拉压子午线分为“岩石Ⅰ类”和“岩石Ⅱ类”两部分进行比较。各准则对应的拉压子午线与试验数据的比较如图5所示。图5中各准则中的参数取值需由强度特征值和由岩石软硬程度、破碎程度而定时,取值方法[49,64-68,71-72]见表6,准则参数取值方法由数据拟合的各参数取值见表5,由于三参数非线性双剪强度理论[62]中需要用最小二乘法进行拟合的参数,其含义与Hoek-Brown理论[45]中的参数含义相同,为方便对比,本文采用的各参数取值与Hoek-Brown理论的参数取值相同,由图5可见:
1)单剪强度理论中Mohr-Coulomb理论[2]预测值整体偏低,Griffith理论[47]在压应力区预测值偏低,Hoek-Brown[45]理论与岩石拉压子午线上的三轴试验数据变化规律较一致,但由于未考虑中间主应力的影响,Hoek-Brown理论的偏平面比相应的试验数据偏低;
2)岩石八面体强度理论中 Mogi[48―49]、Kim-Lade[54]、史述昭-杨光华[53]、Aubertin[57]、章连洋-朱合华[60]、姜华[61]准则等岩石八面体强度理论与“岩石Ⅰ类”和“岩石Ⅱ类”拉压子午线上的三轴试验数据变化规律较一致,其中 Mogi和Kim-Lade准则中参数是由数据拟合而确定;此外,Argyris-Gudehus[50―51]准则与“岩石Ⅱ类”拉压子午线上的三轴试验数据变化规律较一致,而与“岩石Ⅰ类”拉压子午线上的三轴试验结果吻合略差;
3)双剪强度理论体系中,两参数和三参数线性双剪强度理论与“岩石Ⅱ类”的拉压子午线上的三轴试验数据变化规律较一致,而与“岩石Ⅰ类”试验数据吻合略差,三参数非线性双剪强度理论与“岩石Ⅰ类”和“岩石Ⅱ类”的拉压子午线上的三轴试验数据变化规律较一致。

表5 各岩石强度理论表达式Table 5 Expressions of rock strength theory

(续表)
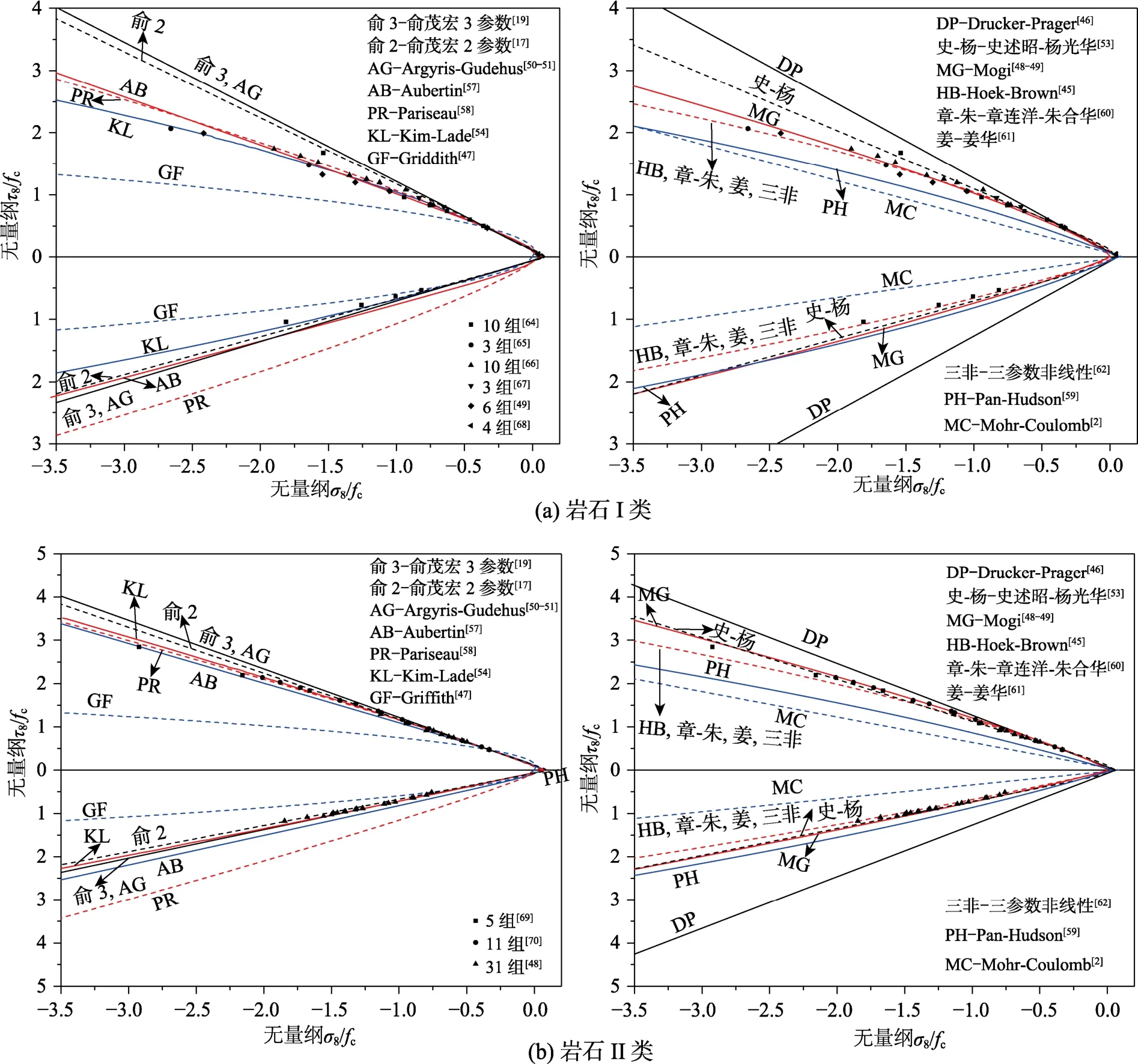
图5 各岩石强度准则对应的拉压子午线比较Fig.5 Comparisons of rock strength criterion between tensile and compressive meridian and experimental data

表6 各岩石强度准则参数取值列表Table 6 The parameter value of rock strength criterion
由于各准则数量较多,选取在与岩石拉压子午线上的三轴试验数据变化规律较一致的强度准则,该类准则对应偏平面图与试验数据的比较如图6所示,可见各准则的偏平面变化规律基本一致。
岩石各准则与试验数据八面体剪应力比较的均值和离散系数见表7,由于岩石三轴破坏包络面上的试验数据点分布并不匀称,对于“岩石Ⅰ类”,姜华强度理论[61]与试验结果相比精度最高,Kim-Lade强度理论[54]次之;对于“岩石Ⅱ类”,三参数非线性强度理论[62]与试验结果相比精度最高,Mogi强度理论[48―49]次之。

图6 各岩石强度准则对应的偏平面比较(σ8/fc =_1.5)Fig.6 Comparisons of rock strength criterion between deviatoric plane and experimental data(σ8/fc =_1.5)
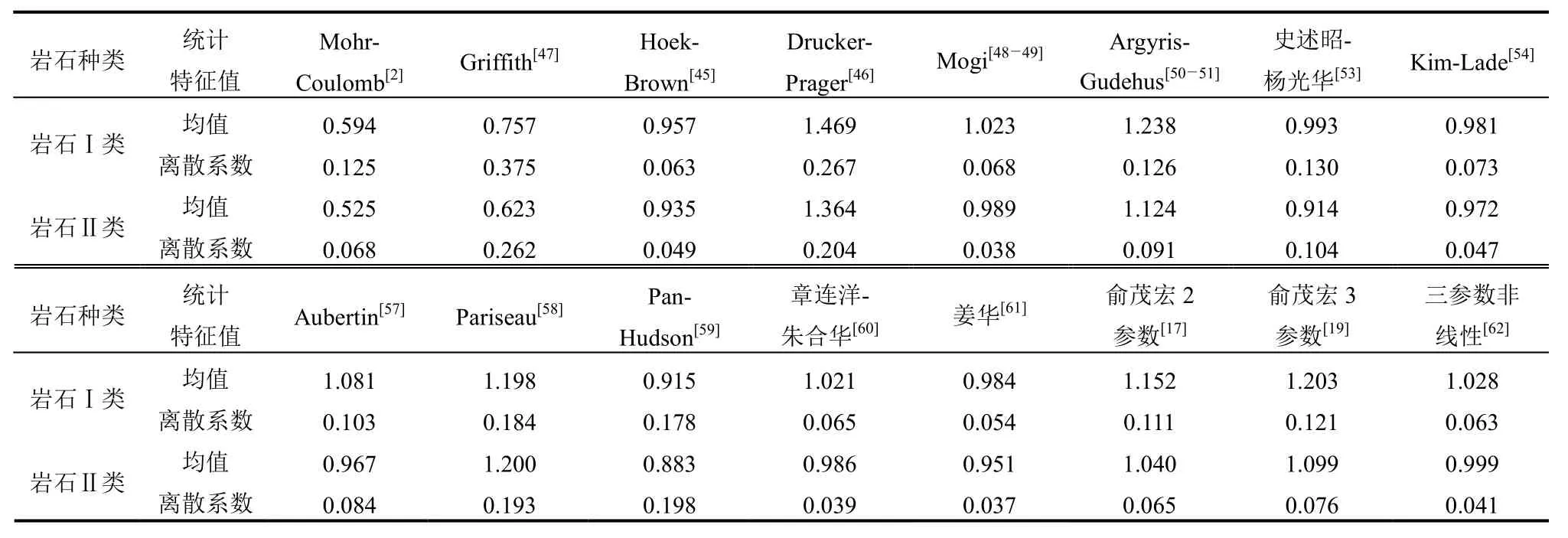
表7 各岩石强度准则与试验数据比较统计表Table 7 Comparisons of rock strength criterion by researches between predicted results and experimental data
3 总结与展望
3.1 总结
材料的破坏与强度理论是一个普遍而又重要的科学问题,100多年来国内外学者对混凝土、轻骨料混凝土和各向同性岩石材料的强度理论开展深入研究,通过对现有各种强度理论成果的比较与总结,结论如下:
(1)古典强度理论概念明确,表达式简单,参数少且易于确定,其中第一理论适用于脆性材料的单轴、双轴与三轴受拉应力状态,第二强度适用于脆性材料的二轴和三轴拉/压的部分应力状态,第三与第四强度理论适用于塑性材料,但是古典强度理都难以准确反映复杂应力状态下混凝土与岩石材料的强度变化规律。
(2)Mohr-Coulomb单剪强度理论形式简单,不考虑中间主应力对材料破坏的影响而参数易于确定,计算结果偏于安全,广泛应用于岩石工程计算。
(3)八面体强度理论采用数学表达式对材料破坏包络面进行拟合,可应用于混凝土、轻骨料混凝土和各向同性岩石等土木工程材料,其中Kotsovos混凝土八面体强度理论、宋玉普-赵国藩轻骨料混凝土八面体强度理论,以及Mogi、姜华等岩石八面体强度理论与各材料三轴试验数据变化规律较一致。
(4)双剪强度理论也可应用于混凝土、轻骨料混凝土和各向同性岩石等土木工程材料,该理论包含了从双参数到五参数,参数取值主要由强度特征值来确定,因而不同特征点下的破坏包络面差别较大,其中的双剪强度理论中的四、五参数双剪强度理论与混凝土三轴试验数据变化规律较一致,三参数非线性双剪强度理论与岩石三轴试验结果变化规律较一致。
(5)主应力空间损伤比强度理论将混凝土受压损伤比(vD,c>0.5,体积膨胀)和受拉损伤比(vD,t<0.5,体积收缩)作为强度准则的2个基本参数,该理论的三轴破坏面光滑连续,由于受压损伤比仅考虑了Lode角而忽略了静水应力的影响,与试验结果变化规律相比,该准则在混凝土处于较高静水压力状态时略偏大,而在较低静水压力状态时略偏小。
3.2 展望
混凝土、轻骨料混凝土与各向同性岩石等土木工程材料都具有单轴抗拉压强度不等以及单轴抗压与双轴等压强度不等力学特性,主应力空间损伤比强度理论将受压损伤比(vD,c>0.5,体积膨胀)和受拉损伤比(vD,t<0.5,体积收缩)作为强度准则的2个基本参数,拉、压损伤比的概念可以符合混凝土与岩石等土木工程材料单轴力学特性,也符合混凝土与岩石等材料单轴抗压与双轴等压强度不等力学特性,如损伤比为0.5时可退化为古典强度理论中的第四强度理论,由于作者初期提出的受压损伤比仅考虑了 Lode角而忽略了静水应力的影响,该准则在处于较高静水压力状态时理论与试验结果有一定的误差,因此作者将根据混凝土、轻骨料混凝土与各向同性岩石等土木工程材料的多轴试验规律,提出考虑Lode角和静水应力影响的各类土木工程材料受压损伤比表达式,确定各类土木工程材料受拉损伤比参数取值,提出完善的各向同性土木工程材料主应力空间双参数损伤比强度统一理论。
此外部分岩石具有明显的各向异性或正交异性特征,该类材料的强度理论有待深入研究。
附录:
σ1最大主应力
σ2中间主应力
σ3最小主应力
I1=σ1+σ2+σ3应力张量第一不变量
I2=σ1σ2+σ2σ3+σ3σ1应力张量第二不变量
I3=σ1σ2σ3应力张量第三不变量
θ=0°~6 0° Lode角
