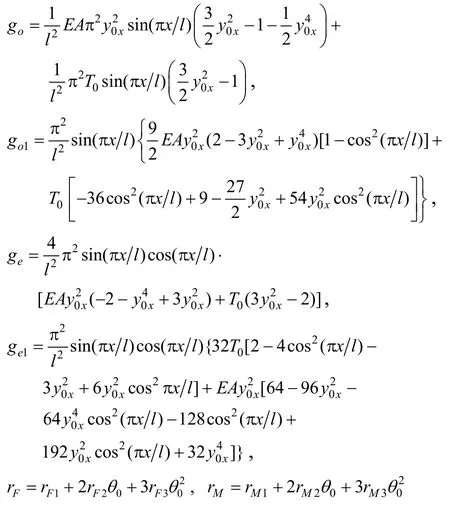高阶扭转模态耦合下覆冰导线的稳定性和影响因素分析
2020-02-10刘习军
霍 冰,刘习军,张 锐
(1.天津科技大学机械工程学院,天津 300222;2.天津市轻工与食品工程机械装备集成设计与在线监控重点实验室,天津 300222;3.天津大学机械工程学院,天津 300072)
输电导线上附着的冰雪改变了导线的圆形截面,形成了非圆截面,而风场作用在非圆截面会导致气动力失稳,诱发自激振动。由于导线具有小刚度和低阻尼的特点,振动频率低、幅度大,导线形态瞬息万变,像跳舞一样,又故名舞动。
为了研究导线在露天环境下的舞动规律,通常将导线模型大致分为 4个自由度(图1):面内(Oxy平面)、面外(Oxz平面)、扭转以及轴向振动。面内振动因其舞动幅值大,危害程度高,是最常见的模型[1]。随着扭转激发机理的提出[2],面内-扭转耦合模型也较为常用[3-5]。此外为了更全面地考察导线的舞动特性,面内-面外耦合模型[6-7]、面内-面外-扭转耦合模型[8-13]、面内-面外-轴向[14]、面内-面外-扭转-轴向耦合模型[15]也逐渐发展起来。

图1 覆冰导线模型Fig.1 The model of iced conductor
以上研究大大推进了覆冰导线动力学模型研究的进程。而后学者们发现舞动有类似波动的特性,仅各自由度的一阶模态振动并不能完全描述导线的舞动行为,因而关于面内多阶模态耦合的模型逐渐被应用[16-18],初步模拟了导线的波动行为。然而在面内多阶模态耦合的模型中,扭转振动往往由于其小振幅的特点被忽略,但在作者的研究中发现[19],扭转模态的振幅虽小,却可以定性地影响面内模态的舞动行为。
本文建立面内前四阶和扭转前四阶模态耦合的动力学模型,研究在多阶扭转模态参与下,面内及扭转模态随参数变化的舞动规律。利用分岔理论研究各阶模态的失稳临界参数,并借助数值模拟进行验证,完善覆冰导线的舞动机理和舞动规律,为工程上导线的敷设和优化提供理论支撑。
1 力学模型
覆冰导线采用图1中模型,Г0表示导线在风偏平面内的初始位置,Г代表导线在任意时刻t的空间位置。导线档距长l,均匀风场U沿z轴方向作用于导线。v、w、θ分别为t时刻导线在x位置处面内、面外和扭转方向的位移。θ0为初始时刻时非圆截面对称轴线偏离z轴的角度。α为风攻角,FL和FD分别为气动升力和气动阻力。
利用 Hamilton原理建立覆冰导线的连续体动力学模型[17]:

式中:E和G分别为导线的拉伸和剪切弹性模量;A和I分别表示导线的横截面积和极惯性矩;T0为导线的初始拉力;y0表示导线的初始悬链线方程;m和J分别为覆冰导线单位长度质量和转动惯量;Fy和Fz分别为FL和FD在y轴和z轴上投影的代数和;M表示作用在截面上的气动扭矩。
借助伽辽金法对偏微分运动方程进行模态截断[20],设振型函数:
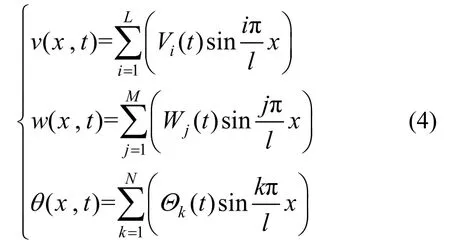
由于导线面内舞动的振幅和危害程度远大于面外舞动,故令M=0;又因为经实验观测到的面内1阶、2阶模态振幅较大,3阶模态振幅较小,而第四阶模态的振动几乎观测不到[19,21],故截取前四阶模态进行研究。令L=4、N=4可得到面内前四阶和扭转前四阶模态耦合的常微分动力学方程:
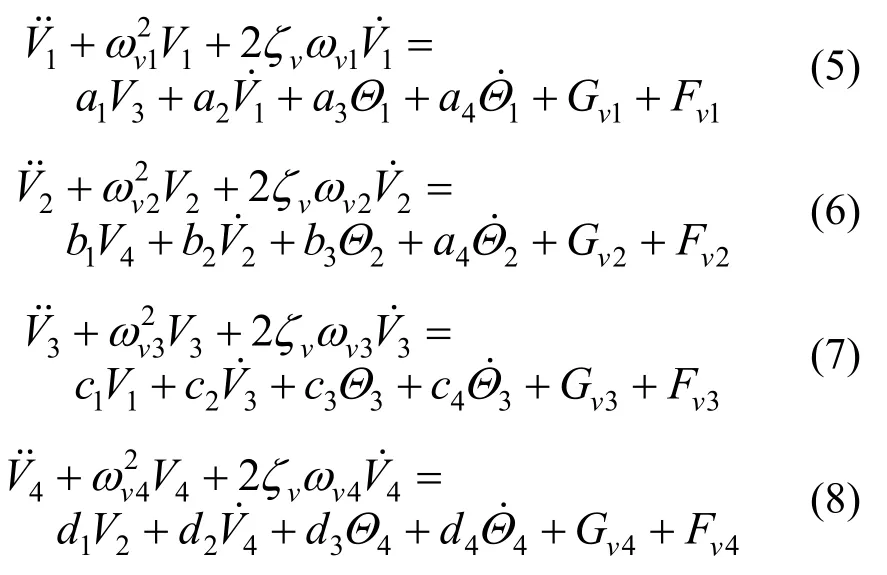
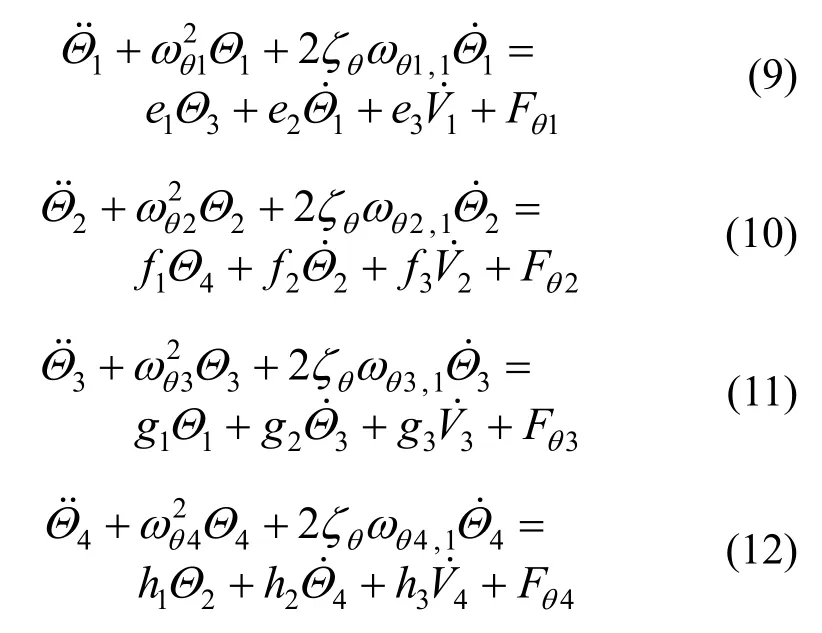
其中:a1~h1为覆冰导线在自重载荷下产生的线性项系数,其余系数为气动载荷产生的线性项系数,具体表达式见附录。Gvi和Fvk分别为几何载荷和气动载荷引入的非线性项。
2 稳定性分析
利用分岔理论对式(5)~式(12)的线性部分进行特征值分析[22],方程组(反)对称模态之间的线性部分线性相关,而对称模态与反对称模态之间的线性部分线性无关,因而取系统的Jacobi矩阵形式如下:


3 影响因素分析
计算系统式(14)的特征值λi,若特征值实部Re(λi)<0,则系统稳定,若Re(λi)>0,则系统失稳进行舞动,Re(λi)穿越零轴时对应的参数即为系统的临界失稳参数。为考察扭转模态参与下导线的舞动行为和舞动规律,将分别在不同环境参数下研究导线的失稳临界条件,导线系统参数见表1[8,23]。
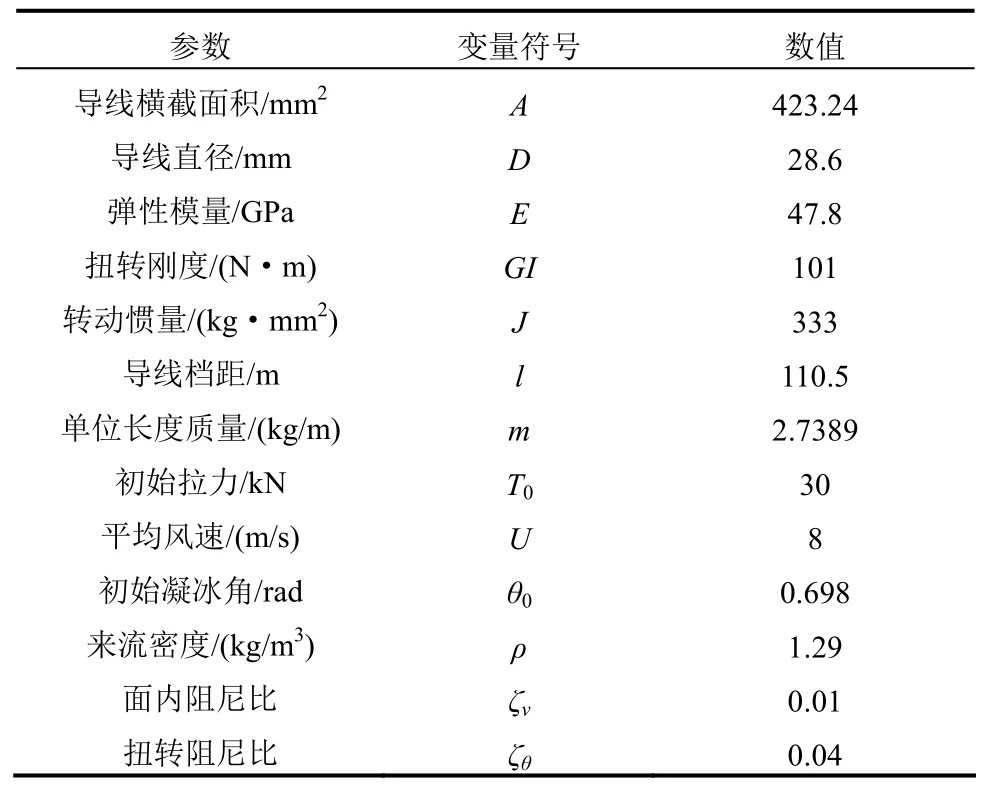
表1 覆冰导线系统参数Table 1 Parameters of iced conductor
3.1 风速
考虑了扭转前四阶模态的系统与文献[17]中只考虑了扭转第一阶模态的系统有着定性的区别(图2(c)),只考虑扭转第一阶模态时,面内第一阶模态先后经历两次 Hopf分岔,随风速增大先失稳而后恢复稳定状态,呈限幅振动,其余面内模态只经历了一次 Hopf分岔,失稳后未恢复稳定状态;而该系统中,面内前四阶模态均经历两次 Hopf分岔,呈现出限幅振动(图2(a)),且随着模态阶数的升高,Hopf分岔点右移,起振风速增大,舞动风速区间增大。例如面内第一阶模态的舞动风速区间为1.75 m/s~12.05 m/s,而面内第四阶模态的舞动风速区间为7.7 m/s~43.94 m/s。图2(b)中,扭转前四阶模态均经历了一次Hopf分岔,随着模态阶数的升高,Hopf分岔点同样发生右移,起振风速增大。该图2(a)和图2(b)表明,随着风速的增大,面内高阶模态会代替低阶模态的舞动;与此同时,扭转模态会代替面内模态的舞动。

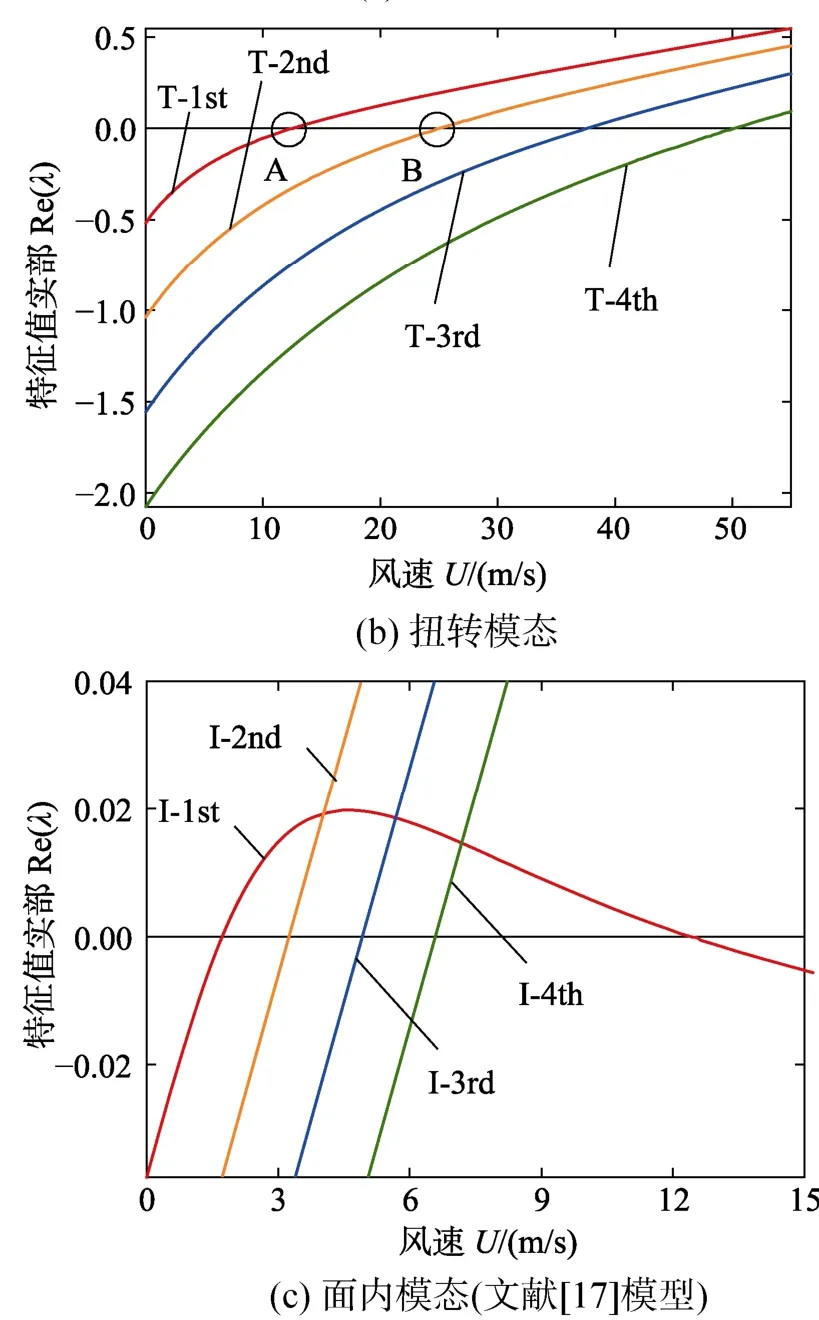
图2 风速对特征值实部的影响曲线Fig.1 Response curve of wind velocity on the real part of eigenvalue
3.2 扭转阻尼比
由于面内和扭转各阶模态稳定性随风速的响应规律基本一致,故以面内和扭转第一阶模态为例,研究扭转阻尼比对临界风速的影响,即选取不同的扭转阻尼比,分别描绘特征值实部随风速变化的响应曲线。
若不考虑扭转自由度,即令式(2)中N=0,以面内第一阶模态为例,此时得到的特征值实部随风速变化基本呈线性关系(图3(a)),只经历了一次Hopf分岔,而扭转自由度的加入改变了原面内模态特征值实部随风速响应的线性关系,使其先后经历了 2次 Hopf分岔。虽然扭转阻尼比的增大可减小扭转模态的舞动,但却使得面内模态的第2个Hopf分岔点右移,增大了面内模态的舞动风速区域,由此,面内和扭转模态在能量上实现了相互转换。当扭转阻尼比增大至无穷大,在此特殊工况下,本文模型等同于未考虑扭转模态模型的计算结果,表明本文模型更加完善。
值得说明的是,舞动系统为自激振动系统,由式(5)~式(12)可以看出,振动方程的阻尼项不仅来自于导线自身的阻尼,还来自于气动力提供的负阻尼,因此当导线自身扭转阻尼比ζθ>1时,扭转模态仍有可能失稳发生振动。
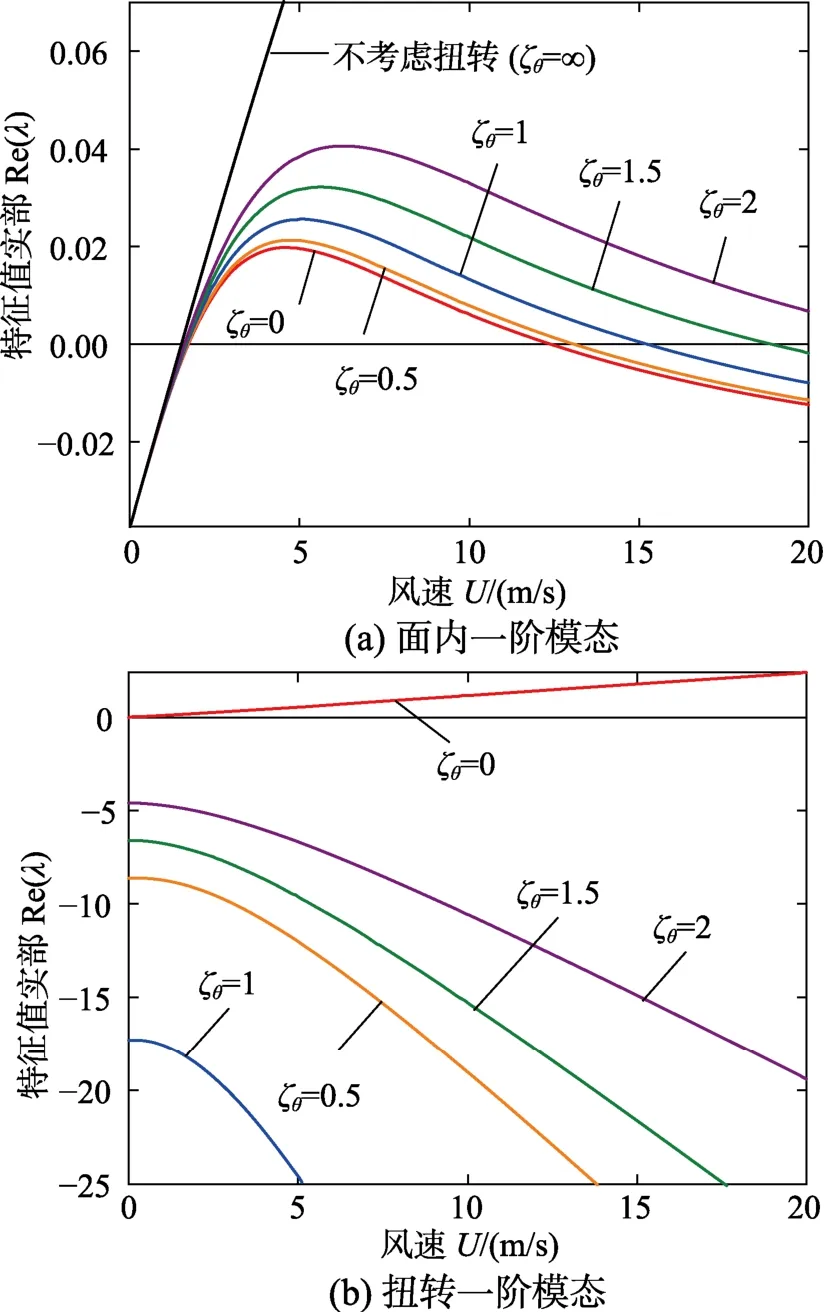
图3 不同扭转阻尼下风速对特征值实部的影响曲线Fig.3 Response curve of wind velocity on the real part of eigenvalue with different torsional ratios
扭转模态特征值实部关于扭转阻尼比并非呈单调性(图3(b)),为了考察这一特性,图4给出了扭转特征值实部随扭转阻尼比的响应曲线。由图4可以看出,当导线扭转阻尼比达到其自身临界阻尼,即ζθ=1时,各阶模态均产生较大的变化。当ζθ<1时,扭转模态的特征值实部随扭转阻尼比的增大而减小,基本呈线性关系,由虚线框内的细节图可以看出,扭转前四阶模态在ζθ很小时便先后穿越零轴达到稳定状态;在ζθ=1附近突然增大,并渐进于一个小于零的数值。因此在第一次穿越零轴之后,扭转特征值实部虽然增大,但不会第二次穿越零轴,始终保持稳定状态。
图4 扭转阻尼比对扭转特征值实部的影响曲线Fig.4 Response curve of torsional ratio on the real part of eigenvalue
3.3 档距
同样以面内和扭转第一阶模态为例,研究档距对临界风速的影响,即不同档距下,特征值实部随风速变化的响应规律。如图5(a)所示,可以看出,随着档距的增大,2个Hopf分岔点分别左移,其中第1个Hopf分岔点小幅左移,第2个Hopf分岔点大幅左移,因此大大减小了导线面内舞动的风速区域。而扭转模态的 Hopf分岔点随档距的增大同样发生了左移(图5(b)),起振风速减小。由此表明,大档距时,导线的面内舞动主要集中在小风速区域甚至消失,被扭转舞动代替。
由于面内舞动危害远大于扭转舞动,因此在保证足够垂直离地距离的情况下,增大档距可在一定程度控制舞动,图5(a)中,档距为400 m时面内舞动消失,但其跨中垂直距离高达15 m,垂跨比过大,因此选取档距为200 m也可基本控制舞动。
3.4 初始拉力
图6以一阶模态为例,描绘了初始拉力对面内和扭转模态稳定性的影响。实线为面内模态的响应曲线(读取左端纵轴刻度),虚线为扭转模态的响应曲线(读取右端纵轴刻度)。从图中可以看出,初始拉力为20 kN时,面内模态舞动风速区域达到最大值,此时改变初始拉力,第1个Hopf分岔点右移,第2个Hopf分岔点左移,舞动风速区域减小;而由于在应用Hamilton方程时,初始拉力不影响导线扭转所产生的变形势能,因而初始拉力对扭转模态稳定性的影响非常小。
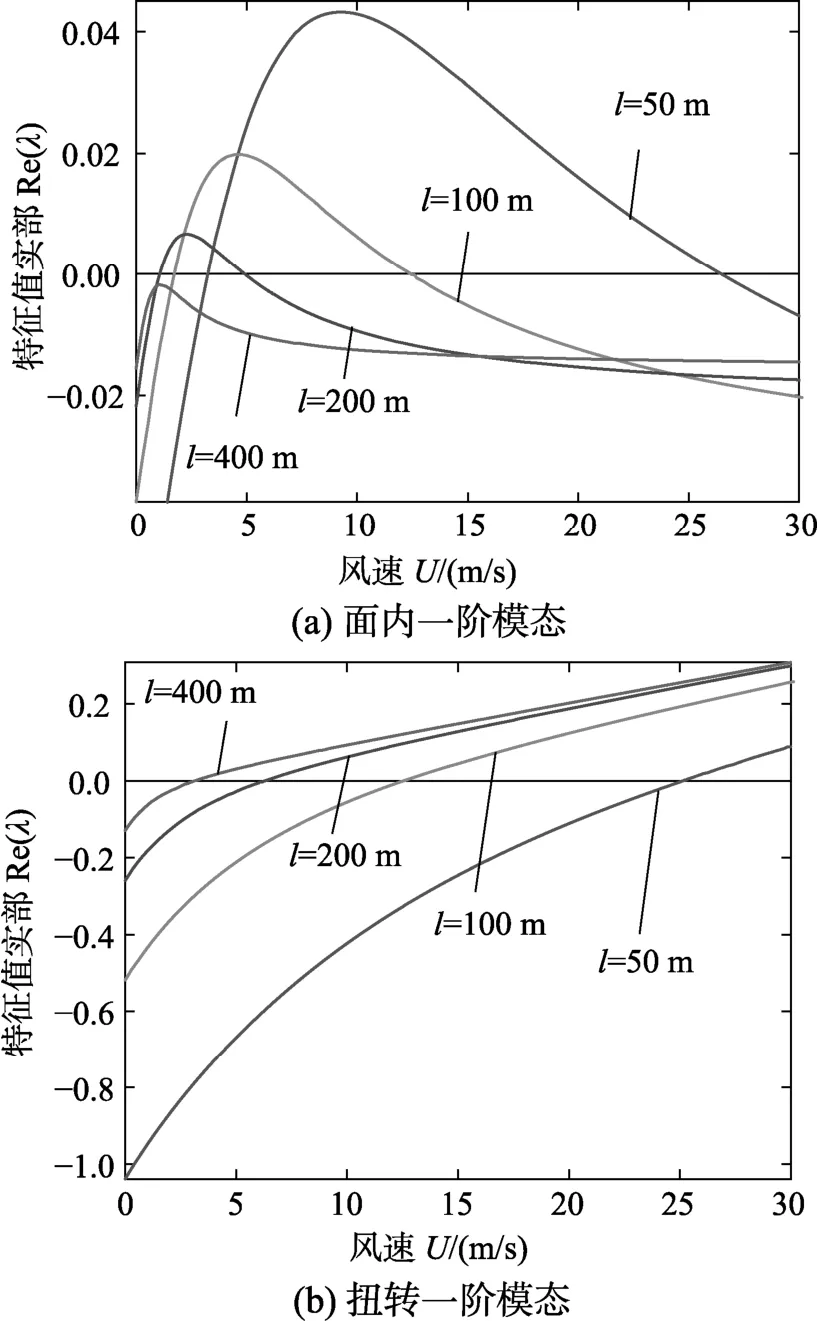
图5 不同档距下风速对特征值实部的影响曲线Fig.5 Response curve of wind velocity on the real part of eigenvalue with different cable lengths
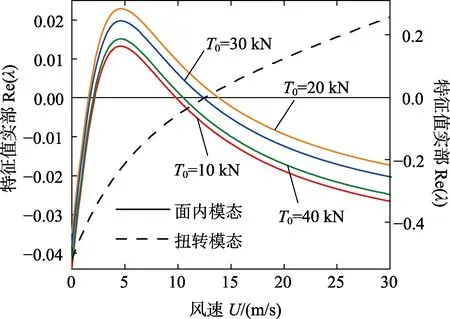
图6 不同初始拉力下风速对一阶模态特征值实部的响应曲线Fig.6 Response curve of wind velocity on the real part of eigenvalue for the 1st mode with different initial tensions
上述分析表明初始拉力对面内模态稳定性的影响并不呈单调性变化,为了更直观地考察初始拉力对各阶模态的稳定性影响,将 Hopf分岔点投影至风速-初始拉力(U-T0)平面(图7),图7中各封闭曲线的内部对应该模态特征值实部大于零的区域即失稳区域;封闭曲线的外部对应该模态特征值实部小于零的区域即稳定区域。可以看出当初始拉力约为20 kN~30 kN时,面内前四阶模态的舞动风速区域均达到最大,当初始拉力小于7 kN或大于75 kN时,面内舞动消失,但考虑到要满足合理的垂跨比和导线强度,可取初始拉力为10 kN或75 kN来达到抑制舞动的目的。
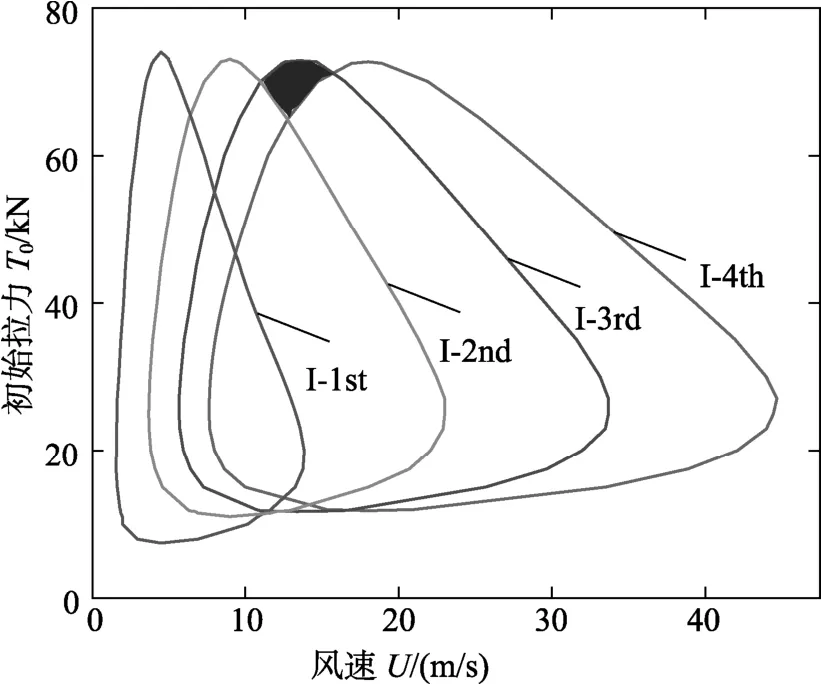
图7 U-T0平面内面内模态的Hopf分岔点集Fig.7 Bifurcation point set of in-plane modes on the plane U-T0
4 数值模拟
为了验证面内和扭转模态失稳临界条件的理论分析结果,取U=13 m/s,T0=70 kN进行数值模拟,其余参数不变。该参数位于图7中的阴影区域和图2(b)中的AB段风速区间(12.8 m/s 数值模拟结果如图8所示,面内运动只呈现出第三阶模态的舞动(图8(a)),与理论结果相同,其舞动频率为2.61 Hz(图8(c)),结合表2可知,面内第三阶模态的舞动频率为其自身固有频率,故该阶模态的舞动是由自激振动引起的。然而不同于理论结果的是,扭转模态的数值模拟结果存在两阶失稳模态,分别是扭转第一阶和第三阶模态(图8(b)),其中第一阶模态的舞动频率为8.02 Hz(图8(d)),第三阶模态的舞动频率为2.61 Hz(图8(e)),参照表2可知,扭转第一阶模态的舞动频率等于其固有频率,为自激振动,与理论结果相吻合;而扭转第三阶模态的舞动频率则与面内第三阶模态的固有频率相同,由此推断,扭转第三阶模态的运动是受到面内第三阶模态的激励而产生的,类似于受迫振动,此行为是由非线性的存在以及模态间的相互耦合作用而引起的。 图8 数值模拟数据图Fig.8 Diagrams of numerical simulations 表2 各阶模态的固有频率/HzTable 2 Natural frequencies of every mode 本文建立了覆冰导线面内前四阶和扭转前四阶模态耦合的非线性动力学模型,利用分岔理论得到了覆冰导线在不同环境参数下的失稳条件和规律,并通过数值方法予以验证,理论与数值结果吻合。主要的研究结论如下: (1)在扭转前四阶模态的参与下,随风速增大,面内前四阶模态先后经历了2次Hopf分岔,呈限幅振动,扭转前四阶模态经历了1次Hopf分岔;大风速时,高阶模态代替低阶模态舞动,扭转模态代替面内模态舞动。 (2)扭转阻尼比的增大会减小扭转模态的舞动,但会增大面内模态的舞动区域,实现面内和扭转模态的能量转换;扭转模态在导线自身扭转临界阻尼ζθ=1附近呈现出迥异的性质。 (3)档距的增大使得面内模态的2个Hopf分岔点和扭转模态的1个Hopf分岔点分别左移,在减小面内和扭转模态起振风速的同时,减小了面内模态的舞动风速区域,在大档距情况下,扭转模态将代替面内模态的舞动。 (4)初始拉力过大或过小都会减小面内模态的失稳风速区域,控制面内模态的舞动,但对扭转模态失稳临界风速的影响非常小。 以上结论对导线的敷设和优化具有指导意义。在覆冰导线舞动中,面内模态舞动的危害远大于扭转模态,因此在敷设导线时主要考虑对面内舞动的控制。在保证足够垂直离地距离时,增大导线的档距或减小初始拉力都可以有效地减小面内舞动。在保证导线强度的情况下,增大初始拉力可达到抑制面内舞动的目的。此外在安装防舞装置时,也应尽量避免在面内模态的结点上安装。此外本文在研究过程中还发现,由于非线性的存在和模态间的强烈耦合作用,覆冰导线系统内部存在模态间的激励现象和内共振行为,将在后续的工作中进一步展开研究。 附录: 其中: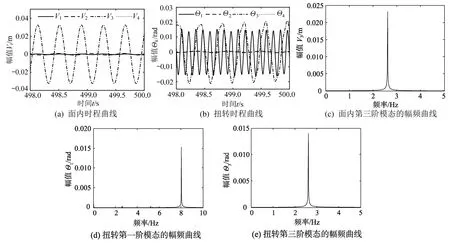

5 结论与展望