基于GNSS 邻域相似性的5G 基站纳秒级时间同步技术研究

刘文学，陈诗军，葛建，袁洪，龚翠玲

（1.中国科学院光电研究院，北京 100094；2.中国科学院大学电子电气与通信工程学院，北京 100049；3.中兴通讯股份有限公司，广东 深圳 518055）

1 引言

随着移动通信业务的迅速增长，无线网络升级演进速度逐步加快。无线网络升级到5G 阶段，不仅网络结构发生变化，而且对于基站间的时间同步精度要求也进一步提高[1]。4G 阶段基站采用全球卫星导航系统（GNSS,global navigation satellite system）实现基站百纳秒量级授时设备授时精度，基站空口时间误差控制在1.5 μs 以内，满足移动通信系统长期演进（LTE,long term evolution）系统的时间同步基本需求。5G 阶段的高精度定位技术、多点协作（CoMP,coordinated multiple point）、载波聚合（CA,carrier aggregation）等增量功能和关键技术[2-5]则对基站时间同步提出了更高的要求，其中移动通信系统LTE-A/5G 阶段的基站间同步需求甚至高达纳秒量级。因此，5G 中基站的高精度时间同步对于5G 网络效能的充分发挥具有重要意义。

当前主流基站授时/时间同步设备包括基于GNSS 的授时技术和基于IEEE 1588 的精确时间协议（PTP,precision time protocol）技术。目前基于GNSS 的授时技术通过GNSS 信号实现接收机的高精度定时，其接收机定时精度在百纳秒量级；基于IEEE1588 的精确时间协议技术将主参考时钟通过1588 光纤网络实现高精度的时间传递，通过有限跳数保持站点间时间同步，其每跳的时间同步精度损失在3～5 ns。2 种技术相互结合能满足移动通信分时长期演进（TD-LTE,time division long term evolution）基站的基本时间同步需求，但是对于5G中诸如基于基站的高精度定位、CA、CoMP 等应用和技术需求的更高精度时间同步需求而言，现有的时间同步技术与设备的精度还存在较大的提升空间。以5G 技术中规定的用户基于基站的定位技术为例[5-7]，实现亚米级的定位误差需要的基站时间同步精度至少应该达到3 ns 量级，如果考虑定位几何精度因子等因素，还期望进一步提高时间同步精度。另外，LTE-A/5G 阶段某些增量功能的启用对基站授时设备的时间同步的需求已达到纳秒量级[8]。

目前的纳秒量级高精度时间同步技术因为成本、技术难度、技术成熟度等原因还未满足LTE-A/5G 阶段高精度时间同步的要求[8-11]，因此尚未全面推广。目前纳秒级高精度时间同步方法的研究主要包括基于本地高稳原子钟的时钟驯服技术[12-13]、基于GNSS 实时动态差分技术（RTK,real-time kinematic）[14]的技术、基于GNSS 精密单点定位（PPP,precise point positioning）的技术[15-17]、基于微波的往返时间（RTT,round-trip time）技术[18]、基于光纤增强的技术[19-20]，这些方法在一定程度上可以满足区域基站的高精度时间同步需求，但都存在不同程度的缺点。基于本地原子钟的驯服技术将原子钟的长稳特性和GNSS 接收机授时的时间长期准确性结合，通过时钟驯服技术提高授时精度，其技术要求终端采用价格昂贵的高稳原子钟且需长时间观测，实现成本较高且应用实时性受限。基于GNSS RTK 的技术采用载波差分GNSS 将区域所有站点的时间同步到参考站时间上，实现各站的高精度时间同步，但由于各参考站的本身时间之间存在不确定偏差，因此在不同参考站边界存在边界峭壁效应（即边界用户存在时间跳变），且该技术条件下的时间同步网络只能是有中心节点形态（参考站即为网络中心节点），网络稳健性和抗毁性较弱。基于GNSS PPP 的技术在理论上可以实现全球任意站点纳秒级高精度的时间同步，但是其技术的实现要求各站采用同一套PPP 模型的外部数据辅助实现，外部辅助数据的获取需要依赖全球几百个参考站的连续高质量观测数据维持，因此该技术对基础设施依赖较大，其服务连续性、自主性和安全性不受控。基于微波RTT 技术采用双向单程/双程时间比对来实现站间高精度时间同步，该技术实现需要额外占用5G 宝贵的频率资源，另外随着节点的增加其时间同步误差存在积累问题，相关技术目前还在进一步研究中。基于光纤增强的高精度时间同步方法通过闭环技术实现网间时间同步误差跳变的修正和较大区域的纳秒级高精度时间同步，其技术需要布设光纤，对基础设施依赖较强，系统成本较高，在很多不具备光纤网络设施的场景无法应用。可见，目前的纳秒量级高精度时间同步技术在满足5G 基站高精度时间同步需求上还存在相关问题，有待进一步研究和解决。

本文针对5G 基站高精度时间同步需求，提出了一种基于GNSS 邻域相似性的纳秒级高精度时间同步理论与技术，在保证全网一定授时精度（百纳秒）的传统授时基础上，提升地理邻近区域站点间的时间同步精度，进一步实现任意20 km 地理区域内各站点之间纳秒级高精度时间同步。相比现有通过提高站点绝对授时精度从而实现时间同步的方法，所提方法具有高精度、时间同步网络无中心点、低成本和低基础设施依赖特点，可以满足5G 基站高精度时间同步需求。本文主要贡献如下。

1)分析5G 基站高精度时间同步需求，提出基于GNSS 信号的邻域相似性的纳秒级高精度时间同步理论。

2)设计纳秒级GNSS 高精度时间同步基站中定时模式、多星联合信号处理算法。

3)研究方法在区域（20 km 区域以内）和全域（广域）地理范围内的时间同步特点分析。

2 5G 基站高精度时间同步需求特点

目前，移动通信时间同步分层网络架构如图1所示。移动通信基站时间同步技术目前主要依靠GNSS 授时接收机完成基站间的授时[21-22]，基于IEEE1588 的电缆或光纤部分作为延伸手段，通过有线方式完成室内或地下部分时间的配送。GNSS 授时接收机通过授时解算，完成50～100 ns 精度的全网时间溯源。IEEE1588 以GNSS 授时接收机的输出作为时间频率源来完成相关网段内的时间频率配送，共同完成移动通信网络的时间同步。目前在该时间同步方式下，基站间时间同步精度在百纳秒量级，基站空口时间同步精度在1.5 μs 内，满足4G/5G 基本的通信需求。

图1 移动通信时间同步的分层网络结构

区别于目前移动通信网络，5G 作为面向智慧城市、车联网、物联网等多样化服务的信息网络，相关增量业务对站间时间同步精度提出更高的需求。5G 中相关技术对于基站间时间同步技术的需求有其具体特点：在5G 基站的高精度位置服务应用中，要求参与定位解算的邻近基站间时间同步精度达到纳秒级即可，而对于地理非邻近基站间的时间同步要求则可扩大至百纳秒；CoMP、CA 技术也针对参与相关处理的邻近基站时间同步精度提出纳秒级高精度要求，而对于地理间隔较远的非协作节点基站间的时间同步精度要求则可扩大至百纳秒。因此，5G 相关高精度时间同步要求可以概括为“地理邻近基站间时间同步精度纳秒级，全网时间授时精度百纳秒”的具体特点。

由以上分析可知，目前移动通信基站间的时间同步精度不能够满足5G 相关新的业务应用对基站间高精度时间同步的需求，主要瓶颈是基于GNSS的授时设备无法实现纳秒级的区域高精度时间同步，基站GNSS 定时精度与5G 相关需求差异较大，限制5G 网络相关增量应用的启用。

3 基于GNSS 的5G 纳秒级区域时间同步技术

3.1 GNSS 邻域相似性与区域高精度时间同步

GNSS 邻域相似特性描述在任意地理邻近区域内，各接收机接收到的任意GNSS 单星信号误差具有相似特性，测距误差具有高度一致性特点。差分GNSS 技术基于此来改善GNSS 接收机定位精度性能，以位置高精度为约束，通过设置已知绝对高精度位置的基准站，使基准站地理邻近用户（一般距离基准站20 km 范围内）获取绝对高精度位置信息。如果以时间高精度为约束，考察建立GNSS 误差邻域相似特性与区域高精度时间同步的关系，则可能基于此相似性，实现站点的授时误差与站点距离建立强相关性，从而利用GNSS 信号实现区域站点间高精度的相对时间同步。

GNSS 主要误差包含卫星星钟误差、卫星星历轨道误差、传播路径上的空间电离层模型误差、对流层经验模型误差、接收机晶振和噪声误差。各项误差对于卫星信号的伪距精度影响不同，特点也不同[23]，以典型的GPS 为例，GPS 授时接收机的授时精度在50～100 ns（GPS 运控系统精度决定）。但如果考察两站伪距误差随两站距离的变化之间的关系，其卫星授时误差与站点间距离具有强相关性，而两站时间同步误差取决于其各项误差之差，因此有可能基于此进一步实现任意地理区域内接收机的高精度时间同步。

任意20 km 邻近地理区域内的各项误差对站间时间同步的影响和表现特性如表1 所示。在相距20 km 下GPS 接收机各项误差中，影响最大的接收机钟漂可以通过解算消除；电离层误差最大为0.7 ns（SA 关闭下）；对流层误差最大为0.7 ns（采用经验模型修正后）；卫星广播星历中的星钟误差对各接收机间时间同步影响相同（即同一颗卫星对于不同用户影响相同）；星历误差是卫星广播星历残差在卫星与接收机连线方向上的投影，其值小于0.08 ns。

表1 区域内（相距20 km）GPS 误差对时间同步的影响

根据以上分析可知，GNSS 信号误差对于任意相距20 km 内的站点来说具有较强相似性，通过选择相应的定时模式与接收机处理算法，结合接收机本身时钟特性进一步减小随机噪声抖动，理论上时间同步误差可达到3 ns 以内，并且同步误差随着两站距离减小而减小。基于此，在传统基于GNSS 信号实现百纳秒级授时基础上，可进一步提升地理区域内站点的时间同步精度，基于GNSS 信号实现任意区域内各基站间的纳秒级高精度时间同步。该方式下，站间时间同步具有“地理邻近基站间时间同步精度纳秒级，全网时间授时精度百纳秒”特点，其时间同步特点与前文分析的5G 对于时间同步特点的需求相契合。

地理20 km 区域内任意2 个接收机信号各误差项虽然呈现表1 所示的误差相似性特点，但实际中GNSS 接收机接收到各个卫星信号之间的误差存在较大差异，远远大于单星测距误差在20 km 范围内地理分布上的差异。目前，普通GNSS 授时接收机在选星、加权算法策略的设计上往往以站点位置误差最小为目标，接收机在同一时刻观测GNSS 卫星状态可能存在的差异、接收机定时解算中位置误差与时差的耦合，使时间同步实测结果即使距离很近的2 台接收机之间也存在如图2 所示的较大误差。实现上述GNSS 信号邻域相似性的表达还有待进一步改进，因此需要针对5G 基站应用特点设计相应的GNSS 接收机定时相关算法。

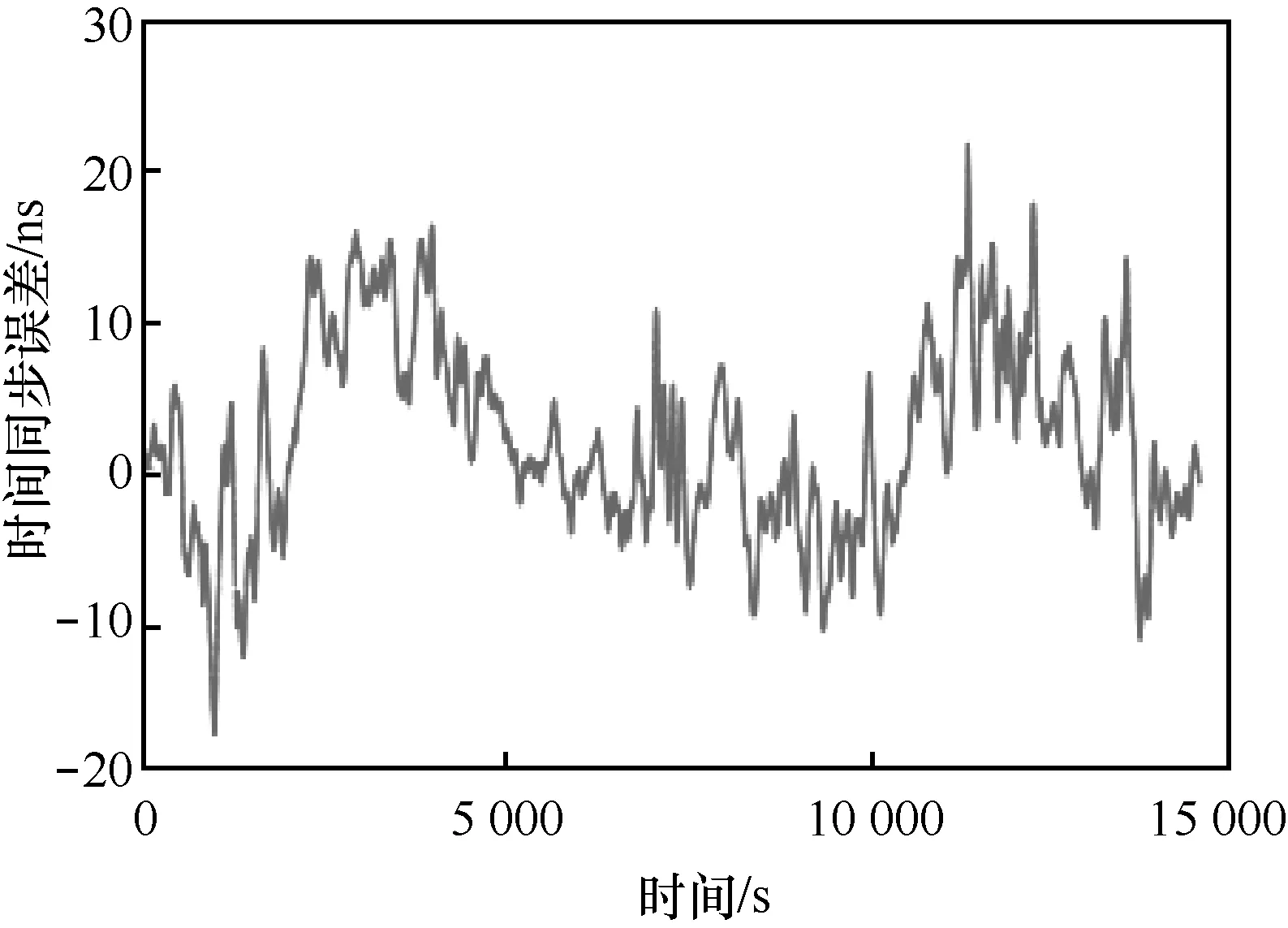
图2 传统基站GNSS 授时接收机超短基线下时间同步误差测试结果（2 台接收机天线2 m 基线下）

3.2 接收机定时解算模式的选择

GNSS 接收机的定时模式有传统基于用户位置未知的位置速度定时（PVT,position velocity and timing）解算模式和用户位置预先已知的固定点位置解算模式，描述2 种解算方式下的解算方程如式(1)和式(2)[18]所示。

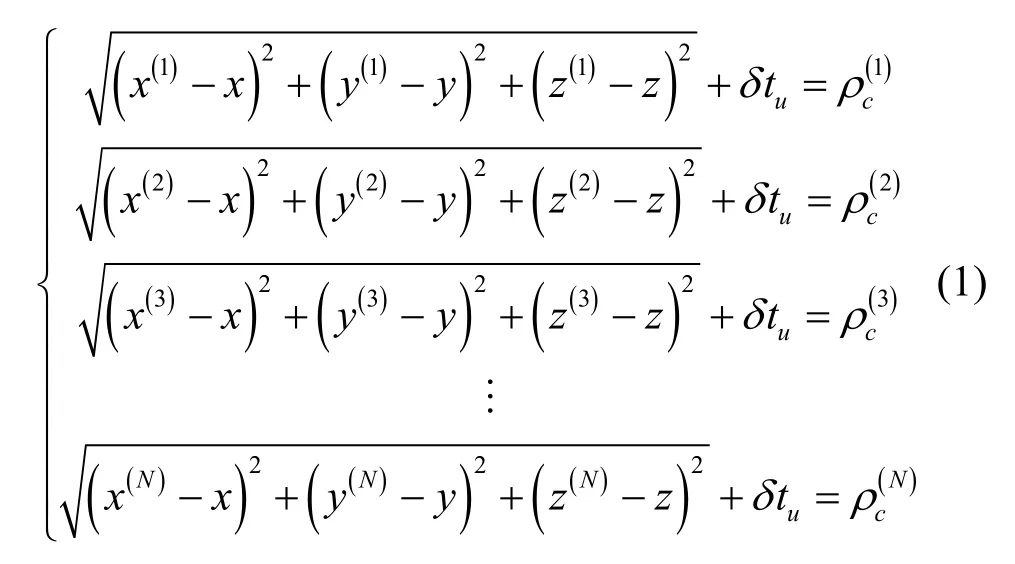
其中，(x(i),y(i),z(i))表示接收机跟踪的第i颗卫星的位置坐标，表示接收机跟踪的第i颗卫星的伪距观测量，(x,y,z)表示待解算的接收机位置坐标，δtu表示待解算的接收机时差，(x0,y0,z0)表示事先获得的接收机位置坐标，表示接收机根据跟踪到的第i颗卫星观测量解算的接收机时差信息。与式(1)所示的传统PVT 解算方式不同，式(2)中基于每一颗跟踪卫星都会解算得到一个接收机时差值。

在传统PVT 解算模式下，用户时差信息和位置信息同时通过式(1)解算得到。该模式下，一方面，伪距相关误差在解算中被归算到接收机时差中，造成接收机时差解算结果和位置解算结果相耦合；另一方面，卫星的几何构型对接收机解算的位置误差的影响也会耦合进入接收机时差解算结果。卫星的几何构型对接收机时差解算的结果影响以精度稀释因子（TDOP,timing dilution of precision）表示，具体如式(3)所示[24]。

其中，TDOP 表示与解算卫星几何构型相关的时间精度因子，σURE表示解算卫星信号的伪距误差标准差，σδtu表示解算用户接收机时差。对于卫星导航系统中典型的GPS 来说，其TDOP 值一般为0.5～2.5[24]，传统PVT 解算实现定时的精度是在卫星观测量测量精度的基础上放大TDOP 得到，基于GPS 的单点PVT 解算实现定时精度在50～100 ns。

若预先已知用户准确坐标，则可以采用式(2)所示的固定点位置解算模式。该情况下接收机的每颗卫星观测方程都会解算出一个接收机时差信息。假设接收机跟踪卫星时差中由于接收机噪声引起的误差为分别相互独立的观测噪声，服从均值为0、方差为的分布，则对于接收机跟踪卫星的噪声水平和各卫星解算时差值，可采取平均或者加权平均进一步减小观测噪声。以最简单的算术平均为例，在各卫星观测噪声服从独立同分布的情况下，其可以将接收机定时噪声方差减小到原来的。因此，与传统PVT 解算方法的噪声相比，采用固定点位置解算模式方法可以降低定时噪声方差。

通过以上分析可知，采用接收机位置固定模式下的定时解算模式，在已知接收机精确位置先验信息下，通过综合处理获取的各星时差结果，可以有效减小接收机定时解算中的噪声误差，提高接收机定时解算的精度；对于移动通信基站应用来说，应用中基站位置一般固定静止，其完全满足接收机位置固定模式下的定时解算应用条件。因此，从原理和具体应用模式上，在基站间高精度时间同步应用中选择接收机位置固定下的定时解算模式较优。

3.3 GNSS 多星联合信号处理算法

如式(2)所示，在接收机位置固定解算模式下，接收机跟踪的各颗卫星都会解算得到一个接收机时差信息。若接收机跟踪的各卫星信号噪声大小相等，则采用算术平均可以达到最优的定时效果。但是在实际中，由于卫星接收信号功率、卫星星历模型、传输链路和接收机天线环境等具体原因，接收机跟踪到的各卫星信号均方误差不相等，从而造成各卫星时差噪声大小不相等[25]，且信号多径最大误差可能高达几十纳秒。此时若采用3.2 节所述的直接算术平均方式，则会造成时间同步噪声恶化。因此需要进一步研究和设计相关的GNSS 多星联合信号处理算法F(·)，具体如式(4)所示，降低接收机解算时差的噪声，提高接收机定时精度。

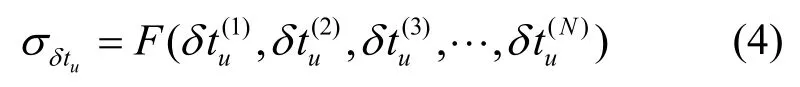
其中，N表示接收机目前解算采用的卫星数目，表示接收机基于跟踪的第i颗卫星计算得到的接收机时差。如式(5)所示，各卫星接收机时差包含表1 所示的各项误差。

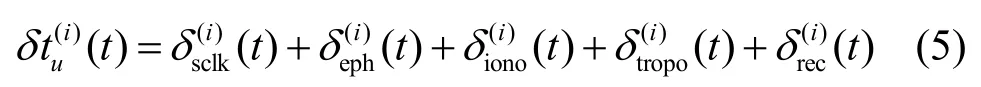
参考文献[26]中观测噪声与卫星高度角模型关系，如式(6)所示。

其中，σ表示观测值中的均方根误差，E表示卫星的仰角。

考虑到卫星仰角和信号载噪比对于卫星时差解算噪声的影响[27]，如果直接设置较高的固定截止角度来剔除接收机跟踪噪声较大的卫星，虽然可减小参与接收机定时解算的卫星伪距观测噪声，但是同时也会造成参与接收机定时解算的卫星数目的减少，从而影响最终时间解算噪声和稳定性。若设置较低的截止角，又会将噪声较大的观测量引入解算结果，影响时间解算的精度。因此，需要设计相关定权模型算法通过高度角加权实现接收机时差解算，既可以保证参与接收机定时解算的卫星数目，又可以实现不同观测噪声下的伪距以不同权重参与接收机定时解算，进一步降低站点接收机定时解算噪声。

图3 是卫星信号的观测噪声均方根误差与卫星仰角的关系曲线。接收机中获得的卫星信号观测噪声的均方根误差与卫星仰角是非线性关系，观测噪声均方根误差随着仰角的增加迅速减小。基于此，在基于仰角的定权模型中，本文通过设置2个角度，即最低截止仰角和饱和截止仰角，将卫星仰角随划分为图4 所示的3 个区段：截止区域、过渡区域和饱和区域。针对接收机跟踪卫星所处的不同区段选择不同的时差加权和处理算法，完成接收机跟踪卫星的多星联合信号处理，实现接收机最优时差估计和解算。

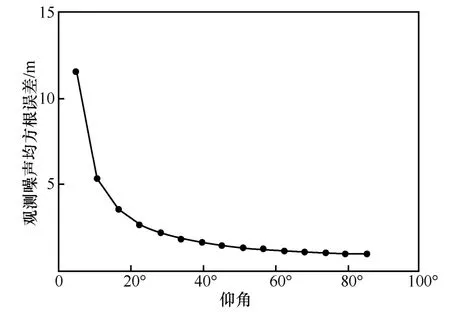
图3 卫星信号观测噪声均方根误差与卫星仰角的关系

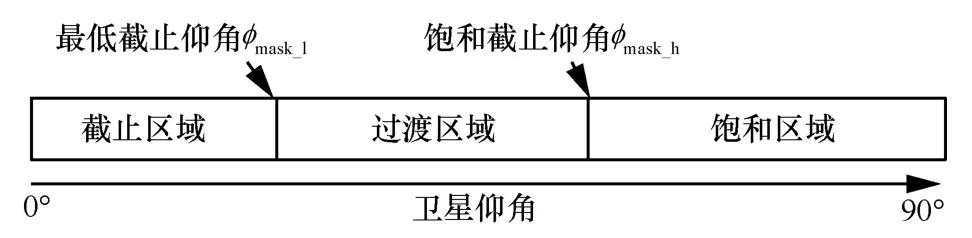
图4 定权模型中卫星仰角的3 个区域

在图4所示的基于卫星仰角的定权模型仰角区域划分中，最低截止仰角φmask_l以下的区域称为截止区域，此区域内跟踪卫星的仰角φ满足φ＜φmask_l，认为卫星的时差误差太大，不参与站点定时的接收时差解算；在最低截止角φmask_l和饱和截止仰角φmask_h之间的区域称为过渡区域，此区域内跟踪卫星的仰角φ满足φmask_l≤φ≤φmask_h，卫星参与接收机定时的时差解算，但其卫星时差以高度角加权方式参与接收机时差解算，高度角越高，权值越大；在饱和截止仰角φmask_h以上区域称为饱和区域，此区域内跟踪卫星的仰角φ满足φ＞φmask_h，认定卫星的时差误差较小，以最大权值为1 参与站点的接收机时差解算。

本文中，选择最低截止仰角φmask_l=15o，饱和截止仰角φmask_h=45o，由此建立如式(7)所示的过渡区域时线性差加权模型。

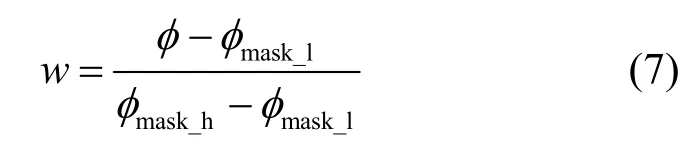
其中，φ表示卫星的仰角，w表示卫星的加权系数。

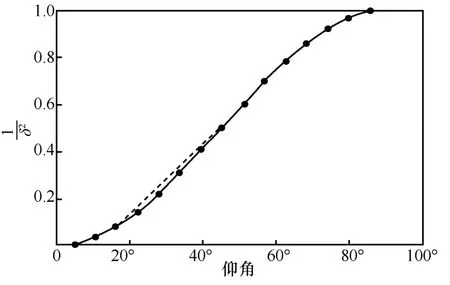
图5与卫星仰角的关系

综上所述，基于卫星仰角卫星时差定权系数计算模型如式(8)所示。

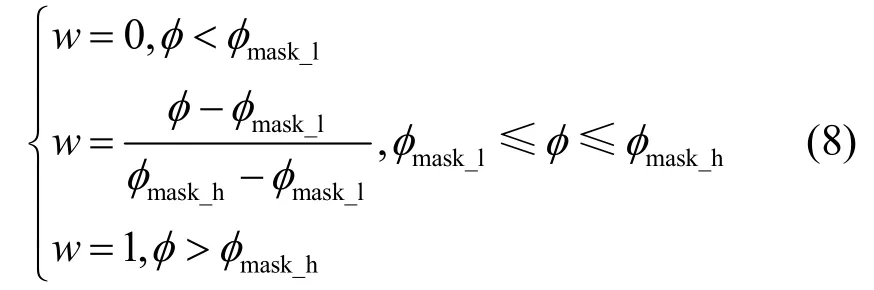
其中，φ表示卫星仰角，最低截止仰角φmask_l=15o，饱和截止仰角φmask_h=45o，w表示通过高度角计算的卫星时差加权系数。最低截止仰角φmask_l和饱和截止仰角φmask_h大小可根据具体情况调整。φmask_l越小，则参与定时解算的卫星数目越多，同时过渡区域的噪声差异越大，导致接收机时差解算误差方差越大；φmask_h越大，导致进入饱和区域的卫星观测噪声越小，但卫星数目变少。此时，站点接收机时差值由式(9)所示的各卫星时差加权之和计算得出。

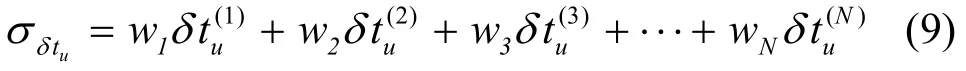
通过严格的数学推导可以证明，式(9)基于加权系数的平均是其参与平均向量的最小二乘估计，且估计是无偏的，该加权估计误差方差小于参与加权估计的最小元素方差。

图6 给出GNSS 多星联合信号处理算法流程，具体如下。

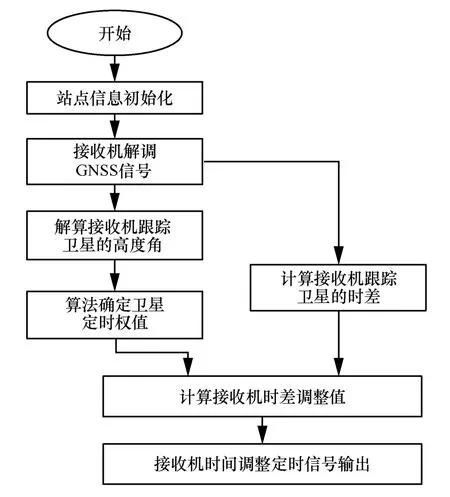
图6 GNSS 多星联合信号处理算法流程

步骤1站点信息初始化，获取本站点准确位置信息。

步骤2接收机解调GNSS 信号，通过导航电文和站点位置获取本站跟踪卫星的高度角信息。

步骤3获取本站跟踪卫星的原始观测量，计算本站点跟踪卫星的时差信息。

步骤4结合步骤2 得出的卫星高度角信息，通过式(8)实时计算站点各跟踪卫星时差信息的加权值。

步骤5结合各跟踪卫星的时差信息和高度角加权信息，按照式(9)求解接收机时差调整值σδtu。

步骤6利用步骤5 解算的时差值修正GNSS授时接收机时间，本站输出高精度定时信号。

区域中的各站点采用如图6 所示的处理算法，得到各站高精度接收机时间信息，完成区域中各站高精度时间同步信息的解算，实现区域各站间的高精度时间同步。

3.4 方法区域与广域时间同步特点分析

本文方法可实现区域站点间纳秒级的高精度时间同步，即任意20 km 范围地理邻域内，实现3 ns以内的高精度时间同步，其各站时差独立解算。该方式下，区域纳秒级高精度时间同步的实现利用3.1节所述的GNSS 邻域相似性原理，区域时间同步时差的中心值是接收机收到该区域各可视卫星时差的平均数。随着站点距离的扩大，邻域相似性减弱，站点间时间同步误差变大。另外，区域内各站点跟踪卫星的集合差异会导致各站定时解算中的可用卫星产生差异，从而导致站间时间同步误差恶化。因此，本文方法下站间时间同步精度与站间距离、站间跟踪卫星集合情况相关。

为了便于分析，假设两站之间不同卫星观测误差独立同分布，参考本文相关分析和文献[28]，仿真中参数如表2 所示，卫星各项误差采用正态分布的随机数仿真。图7 是仿真条件下不考虑信号多径与干扰等因素，两站时间同步误差的均方根随两站可视卫星集合交集卫星数的变化曲线。由图7 可知，随着两站公共可视卫星的增多，两站的时间同步误差均方根明显减小。当公共可视卫星集合数目达到5 颗以上，站点间时间同步精度可以达到3 ns 以内；当两站可视卫星集合完全不相关，其站间时间同步误差均方根可能增大至几十纳秒量级（即GNSS 系统授时误差）。

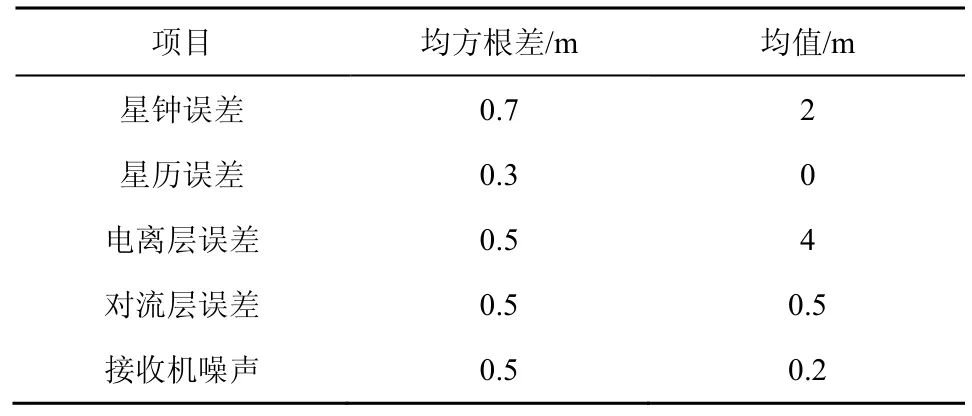
表2 仿真参数列

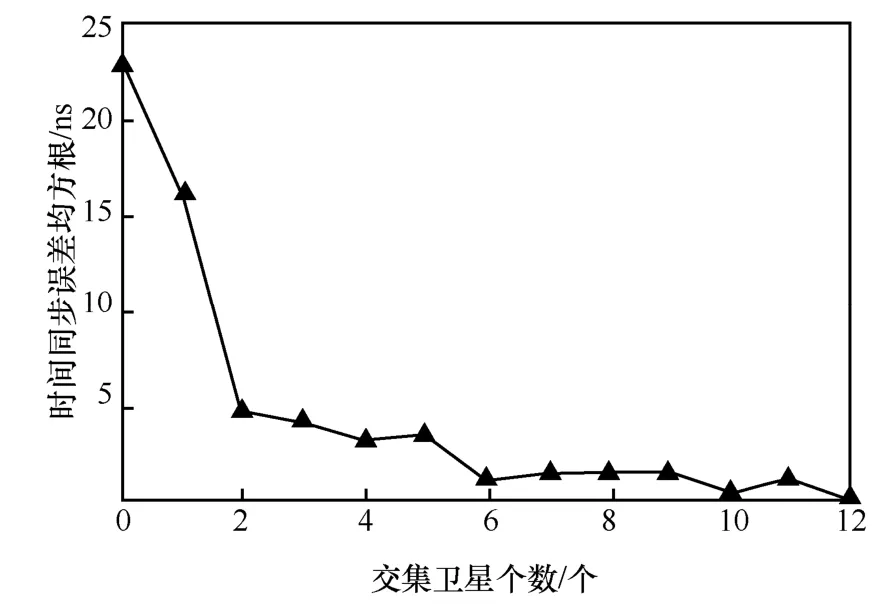
图7 两站时间同步噪声均方根误差随交集卫星颗数变化曲线

通过进一步分析，可得到如图8 所示的本文方法在区域和全域时间同步特点示意。其中水平方向2 个坐标轴表示地理经度和纬度，纵轴表示绝对GNSS 时间。从图8 中可以得出，本文方法下全域时间同步呈现“任意20 km 区域纳秒级高精度，全域丘陵式缓变，最大误差百纳秒且有界”特点，即任意20 km 地理邻域内时间同步精度保持3 ns 以内，全域时间同步/授时误差百纳秒且有边界（边界值大小由各GNSS 系统的运控精度确定），时间通过GNSS 与通用协调时间（UTC,universal time coordinated）实现溯源。其定时与同步特点与5G增量业务对于时间同步特点的需求吻合，满足5G相关业务对高精度时间同步的需求。

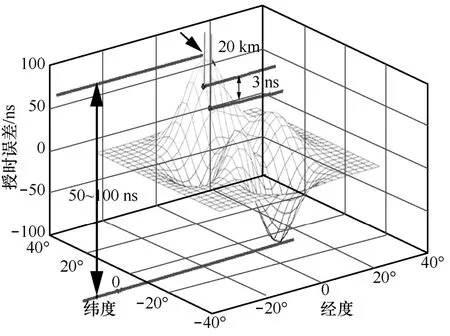
图8 本文方法区域/全域时间同步误差示意

4 仿真与实际结果

在上述相关理论、模型算法的基础上，研制实际的高精度GNSS 时间同步接收机，对相关时间同步算法的具体实现结果进行基于GNSS 卫星信号模拟器和实际天线信号的测试，并对相关测试结果进行分析。

4.1 基于GNSS 模拟器的测试

采用GNSS 模拟器测试的优势是可以控制相关测试场景，排除实际信号中的多径和干扰信号对接收机的影响，实现接收机相关指标的精确评估。在基于GNSS 模拟器的测试中，采用德国iFEN 公司的NavX-NCS 多系统GNSS 卫星信号模拟器，模拟器设置统一静止场景，模拟产生距离2 km 的两站GNSS 射频信号，2 个接收机分别接收两站GNSS信号，计数器采集数据并统计评估2 台接收机的时间同步误差。在测试中，2 台接收机采用自研的GNSS 时间同步接收机，分别采用本文相关算法和传统PVT 解算方法进行2 次测试。图9 和图10 是2台接收机在2 种定时解算方式下，采集10 h 时间同步误差数据绘制得到的时间同步误差曲线。

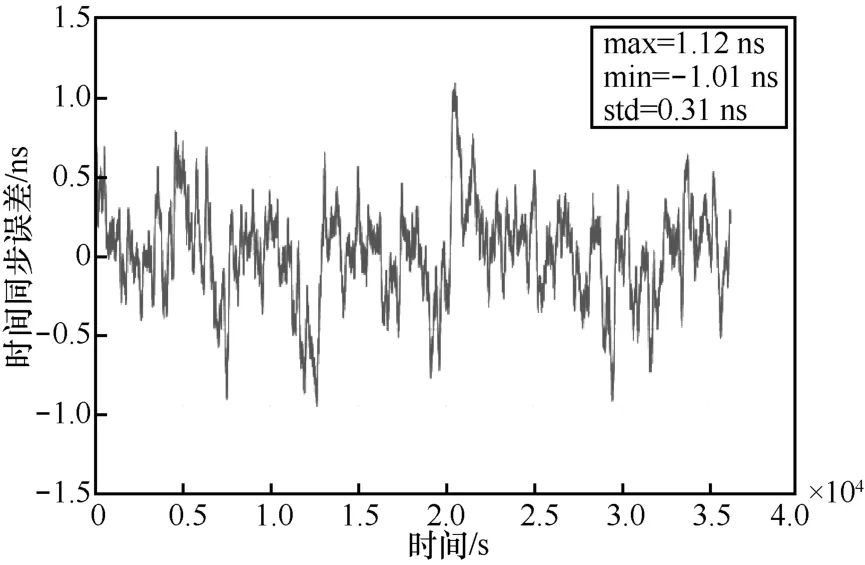
图9 模拟器下本文方法的时间同步误差测试曲线

图10 模拟器下传统PVT 解算方法的时间同步误差测试曲线

2 种方法下2 台接收机时间同步精度统计如表3 所示。通过表3 可知，在模拟器条件下，本文方法实现接收机时间同步精度的均方误差达到0.31 ns，其时间同步误差的最大值、最小值和均方误差均优于传统方法。因此，本文方法在实现时间同步精度方面具有明显优势。但是如前所述，模拟器条件下的测试仅仅验证和评估理想条件下接收机相关指标，关于接收机指标的测试还需要在实际环境下进一步评估和验证。

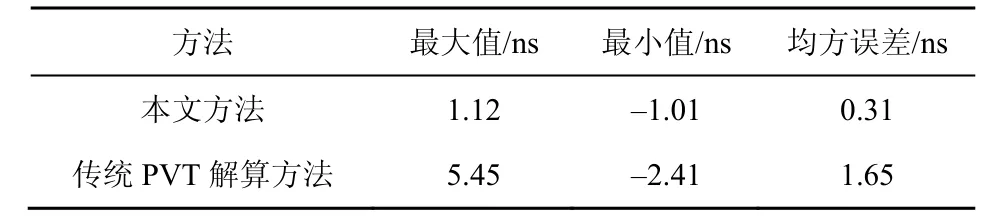
表3 模拟器测试条件下2 种方法时间同步精度统计

4.2 基于实际GNSS 天线的测试

基于实际天线的测试是通过 2 个高精度GNSS 时间同步接收机接收2 个独立的实际GNSS天线的信号，实际评估2 台高精度时间同步接收机的时间同步性能。该测试条件下，2 台接收机的时间同步精度与测试场地GNSS 天线所处的环境和GNSS 的星历具体情况密切相关，其可评估接收机在实际GNSS 信号条件下的时间同步指标。缺点是受限于实际环境和条件，只能实现超短基线下的测试，短基线和长基线下的测试则由于需要太长的天线馈线或两站亚纳秒级的时间同步测试基准而难以实现。

在接收机基于实际GNSS 天线的测试中，采用相距15 m 的2 个NovAtel GPS-703-GGG 型GNSS 天线配合2 台自研高精度GNSS 时间同步接收机完成时间同步指标测试，同时基于某系统标准时测试2 台接收机的授时指标，以验证文中所述的GNSS 误差对授时和时间同步的不同影响：授时精度可能达到几十纳秒，但由于邻域相似性产生的两站时差相似性，两站时间同步精度则可能到纳秒量级。

图11 是实际条件下同样取10 h 的测试数据统计结果曲线。由图11 可知，接收机的授时误差由于GNSS 各项误差影响范围在十几到几十纳秒，但是因为GNSS 信号邻域相似性在接收机中的算法约束表达，使两站授时误差呈现较强的相似性。实际GNSS 天线下2 台接收机时间同步误差曲线如图12所示。由图12 可知，本文方法下区域内接收机之间的时间同步精度可以达到数纳秒量级，但是目前基站GNSS 授时接收机在超短基线条件下时间同步误差依然高达几十纳秒（图2），与本文方法的时间同步结果存在较大差异，可见，相比传统基站GNSS授时接收机，基于本文相关方法的高精度GNSS 时间同步接收机测试结果基本完成如表1 所示的GNSS 信号邻域相似性的表达，实现了区域高精度时间同步。图13 是本次测试中2 台接收机之间时间同步误差的分布统计，可见两站时间同步误差分布呈类正态分布。另外，2 台接收机时间同步误差在图13 中的均值非0，具体原因是2 台接收机之间的硬件时延修正存在偏差，通过GNSS 模拟器可实现该偏差的校准和标定[29]。

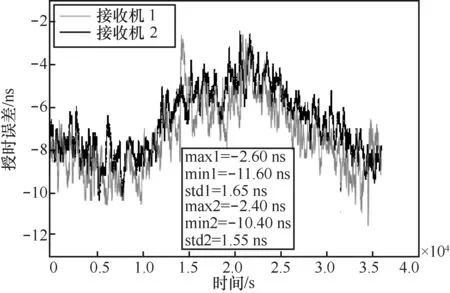
图11 实际GNSS 天线下2 台接收机授时误差曲线

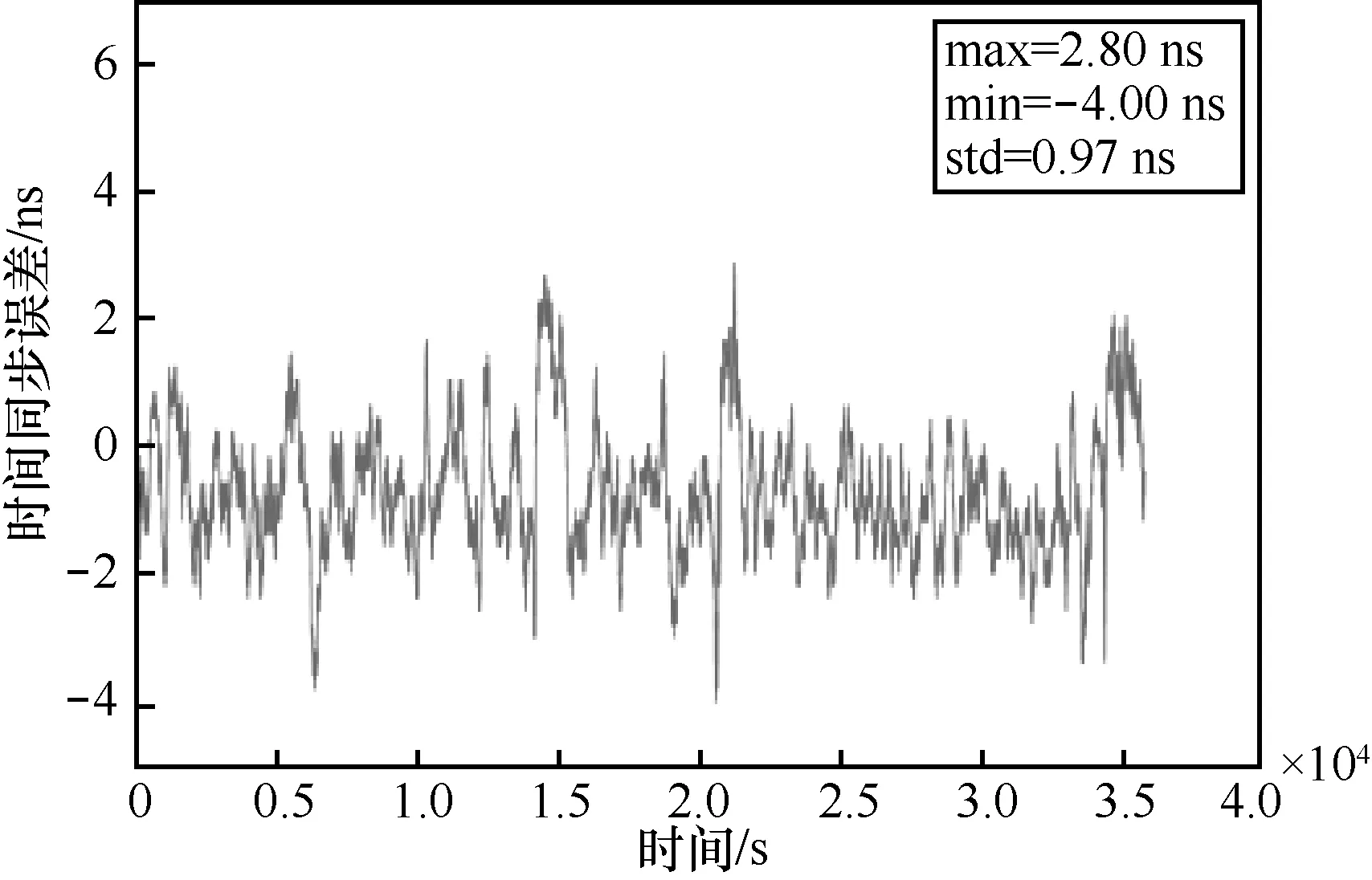
图12 实际GNSS 天线下2 台接收机时间同步误差曲线

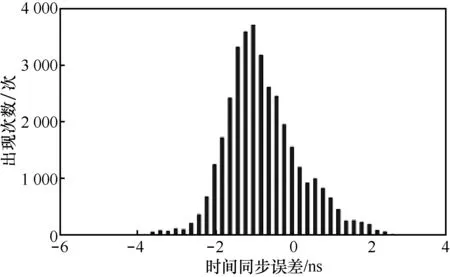
图13 实际GNSS 天线下2 台接收机时间同步误差的分布统计

通过以上的测试结果分析可知，基于GNSS信号邻域相似性原理实现区域纳秒级高精度时间同步从原理和具体实现均具备可行性，即GNSS授时误差可达到几十纳秒，但是其在相距20 km以内的站点时间同步精度可以高达纳秒量级。一般条件下，20 km 地理邻域中各站可视卫星集合基本重合，各项误差满足如表1 所示相似性，时间同步误差可以达到3 ns 以内，且站点时间同步误差随着站点距离减小会进一步减小。另外，接收机硬件时延的差异会影响2 个接收机的时间同步误差的均值，在纳秒级高精度时间同步中需要予以考虑。

进一步分析，如图14 所示，若20 km 地理邻域中站点由于天线架设等原因出现“南北墙”现象导致可视卫星集合出现交集较少或者没有交集的情况（在基站实际架设布置中经常出现），基站间时间同步误差就可能进一步扩大至十几或几十纳秒（图7）。此时可考虑通过多站点时间同步接收机组网，利用多站交互信息联合实现各站时差的精确估计和定时完好性监测，从而实现多站间复杂条件下的纳秒级高精度和高稳健的时间同步，鉴于本文篇幅所限，对此不进行详细讨论。

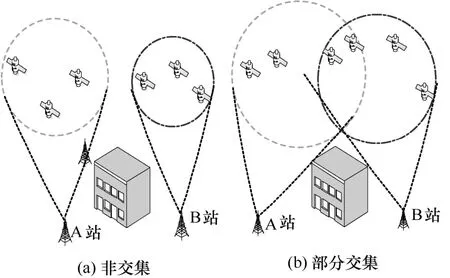
图14 区域内“南北墙”条件下接收机跟踪卫星遮挡的可视卫星集合交集示意（以2 台接收机为例）

5 结束语

本文针对5G 相关增量应用中通信基站间高精度时间同步的需求特点，突破现有GNSS 授时接收机百纳秒定时精度，提出基于GNSS 信号邻域相似性的区域高精度时间同步理论，设计了高精度GNSS 时间同步接收机关键算法信息处理算法，同时分析方法在区域与全域下的时间同步特点，并在高精度GNSS 时间同步接收机硬件中进行了实现和测试验证。本文提出的相关理论方法及相关性能指标通过文中仿真和实际测试进行了验证，结果表明，基于本文方法可实现地理任意20 km 内站点间精度时间同步提升至纳秒量级。该方法成本低，在GNSS 覆盖的地方即可使用，且不需要外部辅助数据，能够满足5G 增量功能的启用对基站间高精度时间同步的要求，为 5G 基站高精度时间同步提供了一种解决方案。文后续的工作中，多站组网实现复杂条件下的多站高精度时间同步相关算法是研究的方向，以进一步实现技术的实际应用环境适应性。