基于自适应加速前向后向匹配追踪的压缩感知重构算法

潘作舟，孟宗，李晶，石颖

（燕山大学电气工程学院，河北 秦皇岛 066004）

1 引言

随着社会的发展，人们的日常生活与工作都对信息的需求与日俱增，导致数据处理的任务量大幅上升，这就要求相关硬件设备与处理算法需要以极高的速度进行更新换代[1]。为了缓解硬件设备与处理算法的更新压力，Cand 等[2]在2006 年提出了压缩感知（CS,compressed sensing）[2-6]理论，该理论能够克服Nyquist 采样定理的限制问题，随机采集到的信号在远低于原始信号维数的情况下，依旧可以通过重构算法进行成功重构，极大地缓解了硬件设备与处理算法的压力。其中，压缩感知理论能够实现低采样率环境下的成功重构，最关键的环节便是重构算法的选取，优秀的重构算法能够保证重构过程的高效率、重构结果的高精度。贪婪类算法和凸优化类算法作为信号重构中的2 类常见算法[7]，皆具备稳定的重构精度，但贪婪类算法因具有较快的速度和简单的框架而得到更加广泛的使用[8]。传统的贪婪类算法主要包括匹配追踪（MP,matching pursuit）算法[9]、正交匹配追踪（OMP,orthogonal matching pursuit）算法[10]、正则化正交匹配追踪（ROMP,regularized orthogonal matching pursuit）算法[11]等。值得注意的是，传统的贪婪算法通常是根据支撑集的大小来确定算法的迭代次数，同时支撑集的大小是通过信号的稀疏度来进行设定的，因此稀疏度的确定直接影响到该类算法的重构精度。而将信号的稀疏度作为先验条件，在实际信号的重构过程中往往难以实现，因此限制了该类贪婪算法的实际应用[12]。文献[13]针对这一局限性提出了前向后向匹配追踪（FBP,forward-backward pursuit）算法，利用前向后向两步策略，逐步扩大支撑集进行重构，实现稀疏度未知情况下的精确重构。在此基础上，文献[14]提出了一种加速前向后向匹配追踪（AFBP,acceleration forward-backward pursuit）算法，根据前向阶段原子的累计权重，来对后向阶段中被删除的原子进行二次选入，减少了FBP 算法的迭代次数和运算时间。但AFBP 算法在二次选入过程中以权重作为判别标准，导致部分错误原子一直存在于支撑集中而无法被删除，影响该算法的重构精度和重构时间。

针对AFBP 中存在的局限性，本文通过改变原子的选入方式[15]，解决后向阶段中的回溯过度问题，得到了一种自适应加速前向后向匹配追踪（AAFBP,adaptive AFBP）算法，该算法具备更高的重构精度和速度。

2 压缩感知和重构算法

2.1 压缩感知策略

压缩感知理论的本质是将采样与压缩相结合，根据信号稀疏表示的先验知识，采用少量非自适应线性测量的方式即可获取原信号足够的信息[16-17]。如待采样信号xN×1，在Ψ域中稀疏，得到压缩感知理论模型为

针对该理论模型，利用观测矩阵ΦM×N对xN×1进行采样（其中M≤N），得到观测向量yM×1，即

可以得到

利用观测矩阵yM×1求信号xN×1是一个欠定问题，无法直接求解。但当xN×1为一稀疏信号时，可以转化为一个求解最小l0范数问题[18]，用公式表示为

式(4)是一个NP-Hard 问题，此类问题计算困难且稳定性较差，但匹配追踪类方法为其近似求解提供了有力的工具。

2.2 加速前向后向匹配追踪算法

FBP 算法属于一种两阶段迭代算法。该算法在稀疏度未知的情况下，通过迭代以固定步长逐步扩大估计支撑集，最后实现对稀疏信号的逼近，虽然具备较高的重构精度，但运算时间较长。AFBP 算法在FBP 算法的基础上，根据前向阶段选入原子的投影值大小，将原子按从大到小的顺序分为s1、s2、s3三部分，并分别为其赋予权重值w1、w2、w3。

在后向阶段删除原子后，并不直接进入下一次迭代过程，而是将删除原子的权重与设定的阈值η相比较。当原子权重大于阈值时，则认为该原子有很大概率为正确原子，再次将其加入支撑集中，即在FBP 算法的基础上增加了一条原子选入的渠道；当原子权重小于阈值时，则认为该原子为错误原子，不再考虑将该原子加入支撑集中。

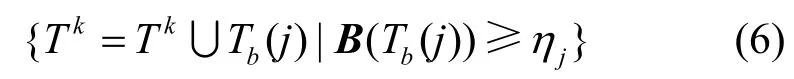
该算法利用每次迭代中候选支撑集的信息，实现对已删除原子的再次加入，以此减少算法迭代次数。相对传统FBP 算法来看，AFBP 算法在保证较高重构精度的前提下，缩短了重构时间。但AFBP 算法在后向回溯过程中根据原子被赋予的权重大小判断该原子是否进行二次选入，这种二次选入的标准需要通过大量选入、大量删除的方式来避免错误原子的选入，增加了算法的运算量。此外，AFBP 算法中原子的权重值是通过迭代过程逐渐累加的，而权重值累加达到阈值条件需要一定时间，因此在迭代前期的加速效果并不明显。而随着迭代次数的增加，一些错误原子权重值逐渐累加达到阈值条件（当阈值设置较小时），错误原子就会被不断选入，导致算法重构的时间增大，重构精度降低。

3 自适应加速前向后向匹配追踪算法

3.1 自适应加速策略

本文针对AFBP 算法中的优缺点，给出了在保证重构精度前提下的自适应加速策略。首先介绍AAFBP 算法中的2 个模糊参数μ1、μ2，其中μ1为前向阶段中原子的选入参数，μ2为后向阶段原子的删除参数。

μ1决定了算法在前向阶段选取原子的数量，当μ1的值比较小时，每次迭代选入的原子数目比较多，算法执行的速度会更快。μ2则控制着每次迭代需要更新的原子数目，μ2越大则每次回溯过程中删除的原子数越多，算法的成功重构率会有所提升，但是算法的执行速度会随之下降。因此算法的成功重构率和重构时间可以通过调节μ1和μ2值来平衡。模糊参数μ1、μ2设定为

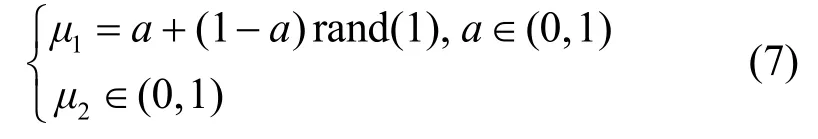
由于在每次迭代中通过模糊参数μ1/μ2选入/删除的原子数目不是固定的，而是由每个原子在历次迭代中的具体情况所决定的，从而使AAFBP 算法在每次迭代中自适应地决定所选入/删除原子的数目。自适应加速策略为：在两阶段回溯过程中，首先根据观测矩阵与残差值之间的乘积值，得到各个原子所对应的相关系数值v。

在前向阶段中，令原子相关系数v中的最大值vmax与μ1的乘积作为前向阶段原子的选入阈值，从而选取相关系数较大的原子放入集合Tf中。

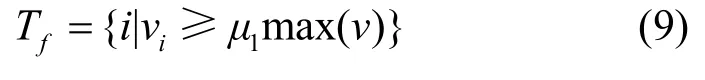
在与前一次迭代所得支撑集合并之后，利用最小二乘法求信号的投影系数，解决了AFBP 算法固定迭代选入的原子数随机性较差[19]的问题。

在后向阶段中，利用删除参数μ2(0＜μ2＜1)来进行原子的自适应删除。找出非零系数对应的索引在Tf里的最大投影系数υmax，将非零系数中大于μ2υmax的全部索引放入支撑集Tk中。这样做的目的是随着迭代次数的增加，当支撑集中增加了新的原子时，则重新计算信号的投影系数，若以前选入的原子对应的系数变小，小于删除阈值μ2υmax，则以前选入的原子可能是错误的，这时通过回溯方式进行删除。按照上述方法进行循环迭代，待达到停止条件时，则完成了对信号的重建，这解决了AFBP算法根据原子权重大小判断该原子是否进行二次选入而存在的运算量过大、重构速度提升较为有限的问题。AAFBP 算法一方面加快了运算的速度，另一方面，由于删除原子依靠的是原子的投影系数大小，因此相对于AFBP 算法来看，错误原子选入的可能性降低，成功重构率将有所提升。

3.2 回溯过度现象

在重构的过程中，为了保证选入原子与残差的正交性，在每次迭代过程中将选入原子对应的观测矩阵列中内容清零来避免原子的重复选入。而在回溯删除错误原子的过程中，正确的原子也有被删除的可能。正确原子一旦被删除，其对应的观测矩阵中内容则被清空，无法被再次选入，影响算法本身的精度，这种现象称作回溯过度现象。图1 展示了不同稀疏度下由于未及时更新观测矩阵导致的正确原子被删除的情况。

图1 在不同稀疏度下由于回溯过度现象删除的正确原子数

由图1 可以看出，随着稀疏度的增加，正确原子被删除的概率近似呈直线增长，而正确原子的大量删除会影响算法的精度。根据AFBP 算法中对删除原子的二次选入方法，对回溯过度现象给出解决策略：首先将观测矩阵Φ中的内容进行备份得到Φ1；其次在每次迭代完毕后，找出回溯删除原子对应的清零矩阵列；最后利用备份观测矩阵Φ1内的信息对清零矩阵列进行恢复。保证在下一次迭代计算残差rk-1与观测矩阵列的相关系数值时，正确原子存在二次选入的机会。

3.3 自适应加速前向后向匹配追踪算法

依据上述加速策略，在每次迭代的前向阶段中，根据原子和残差的相关系数大小自适应地选取原子加入候选集Tf，再将每次迭代选入候选集中的原子加入支撑集Tk中。在后向阶段中，通过设置的删除阈值来选取删除原子加入删除原子集Tb，再通过删除原子集更新支撑集中的内容。在回溯结束后，为了避免回溯过度现象，及时更新观测矩阵列。以此进行循环迭代，直到残差值达到终止条件后，循环结束。算法流程如下。

初始化残差r0=y，初始支撑集Tk=∅，初始索引集Tf=∅。对观测矩阵Φ进行归一化处理。

步骤1利用模糊参数μ1来设置原子的选入阈值，选择原子加入集合Tf。

步骤2对集合Tf中选入原子的相关系数进行正则化处理。

步骤3对观测矩阵Φ中内容进行备份，令Φ1=Φ。

步骤4更新观测矩阵，即{Φα=0|α∈Tf}。

步骤5将最新得到的索引与支撑集合并，即Tk=Tk-1∪Tf。

步骤6最小二乘处理，得到估计信号的投影系数，

步骤7利用模糊参数μ2来设置原子的删除阈值，对支撑集中的原子进行回溯，找到投影系数小于阈值的原子放入集合Tb中，Tb={i|(v)i＜μ2max(υ)}。

步骤 8从支撑集中删除错误原子，Tk=Tk-Tb。

步骤9将删除原子对应的观测矩阵列向量进行还原，即{Φβ内容还原|β∈Tb}。

步骤10残差更新过程，即

步骤11如果满足迭代终止条件||rk||2≤ε，则停止迭代。

输出估计信号

4 实验结果及分析

4.1 参数设置

对于FBP 算法，采用文献[13]中给出的参数设置，即α∈[0.2M，0.3M]，α-β=1，支撑集最大限制参数。对于AFBP 算法，参数α、β以及Kmax与FBP 中保持一致。权重值和阈值参考文献[14]给出：权重分为三层，其中w1=2，w2=1.5，w3=1；阈值参数设置为η1=5，η2=6，η3=7。通过选取合适的参数值，保证AFBP 算法具有较高成功重构率的同时，重构时间较短。

AAFBP 算法中所包含的2 个模糊参数μ1和μ2通过重构实验来进行选取。分别取a={0.3，0.4，0.5}，μ2={0.6，0.7，0.8，0.9}进行信号的重构，重构结果如图2 所示。其中a=0.3，a=0.4，a=0.5 分别用实线、虚线和点划线来表示。而每种线型下4种不同的图形，分别用来表示μ2=0.6，μ2=0.7，μ2=0.8，μ2=0.9 的情况。

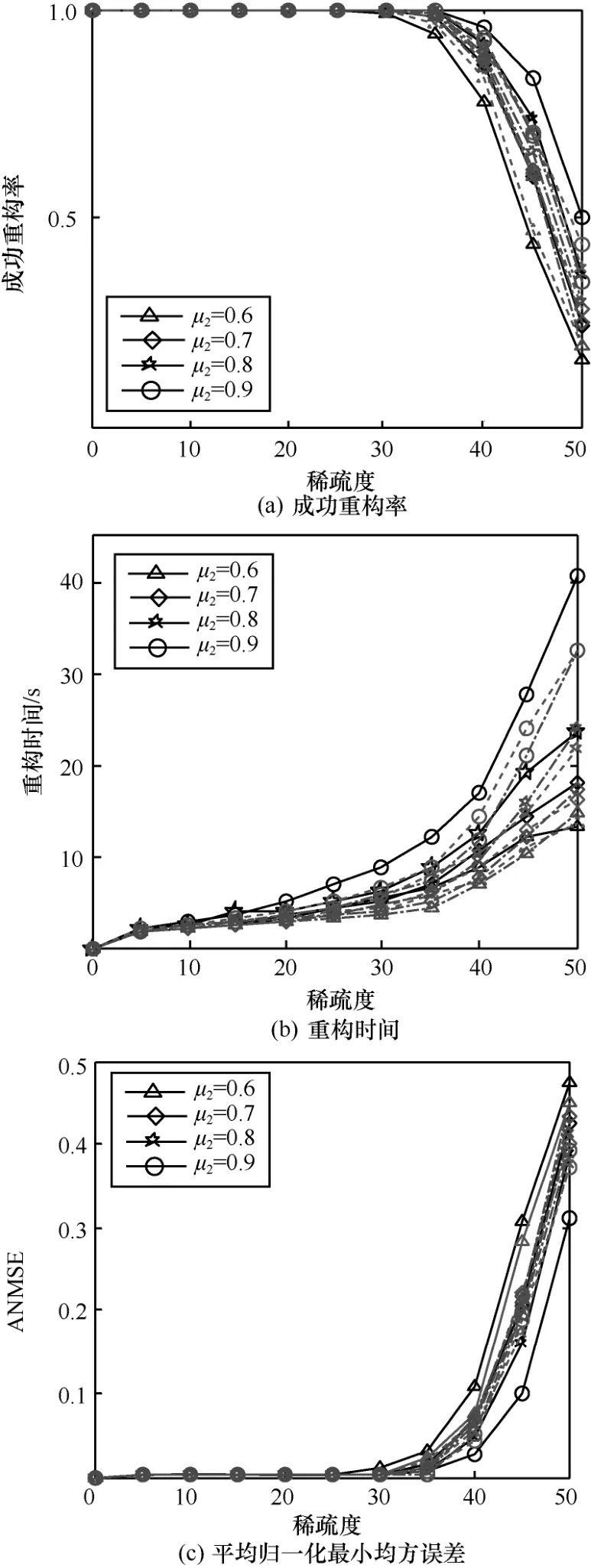
图2 不同参数情况下AAFBP 算法的重构结果比较

从图2 中可以看出，当模糊参数为a=0.4、μ2=0.8时，AAFBP 算法成功重构率仅次于模糊参数为a=0.3、μ2=0.8 和a=0.4、μ2=0.9 这2 种情况。但在重构时间方面相较于二者有较大的缩短，该模糊参数下的平均归一化最小均方误差（ANMSE,average normalized mean squared error）值也相对较小。因此，在后面与FBP、AFBP 算法进行对比时，AAFBP算法的模糊参数设置为a=0.4、μ2=0.8。

4.2 一维稀疏信号重构

实验所采用的稀疏仿真信号长度为N=256，观测矩阵Φ为100×256 的Gauss 随机矩阵，其中稀疏信号非零项分别服从Gauss 和均匀分布。算法迭代终止的阈值大小为ε，其中ε=10-3。

本文以成功重构率来衡量算法的重构精度。其中，成功重构的标准设定为：重构信号与原始信号的最大误差值小于阈值ε1，即，阈值ε1=10-3。每种稀疏度情况下运行500 次，利用总的成功重构次数除以总运行次数来得到该稀疏度下的成功重构率。

平均重构误差则采用平均归一化最小均方误差（ANMSE）进行衡量，定义为

将AAFBP 算法分别与AFBP 算法、FBP 算法进行成功重构率、重构时间以及平均归一化最小均方误差的比较，结果如图3～图5 所示。

1)当观测信号为Gauss 稀疏信号时，AAFBP算法在不同稀疏度下与AFBP 算法、FBP 算法、OMP算法、SP 算法的性能比较如图3 所示。由图3 可以看出，FBP 和AFBP 算法的成功重构率接近且较高。这是由于FBP 算法都具备回溯的过程，因此成功重构率要优于OMP 算法和SP 算法。但回溯操作的引入导致FBP 算法的重构时间较长，其中，AFBP 算法相对FBP 算法的运行时间较短，但是时间缩短的程度并不高。本文提出的AAFBP 算法成功重构率最高，对FBP 算法重构时间的缩短程度要高于AFBP 算法。图3(c)中也显示了AAFBP 算法的相对误差最小。由此可以看出，AAFBP 算法在兼顾重构性能的同时，对于重构时间的缩短也具备优势。

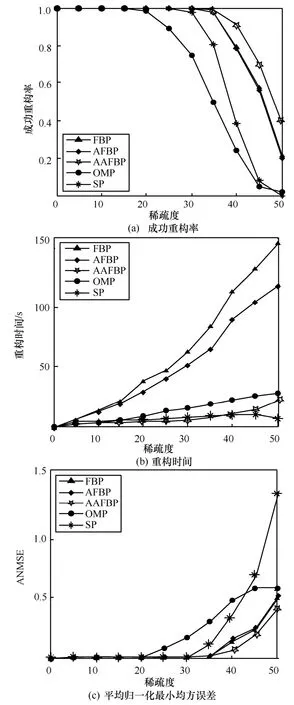
图3 高斯稀疏信号重构结果比较

2)当观测信号为均匀稀疏信号时，AAFBP 算法在不同稀疏度下与AFBP 算法、FBP 算法、OMP 算法、SP 算法的性能比较如图4 所示。图4 测试结果与图3 基本相似，不具备回溯过程的OMP 算法和SP算法的成功重构率相对较低，AAFBP 算法的成功重构率最高，略高于FBP 和AFBP 算法。在重构时间上可以看出，AAFBP 算法较AFBP 算法有明显的缩短，当稀疏度K＜35 时，重构时间在5 种算法中最短；当稀疏度K≥35 后，重构时间依然要短于OMP 算法。在ANMSE 上，AAFBP 算法最低，即平均重构误差最小。对比图3 和图4 可以发现，由于原始信号服从均匀分布时，非零元素幅度差异不明显，通过Φrk-1方式选入错误原子的概率变大，FBP 类算法的重构性能下降，但AAFBP 算法相对AFBP 算法，无论在重构精度还是在重构时间方面，都依旧具备优势。

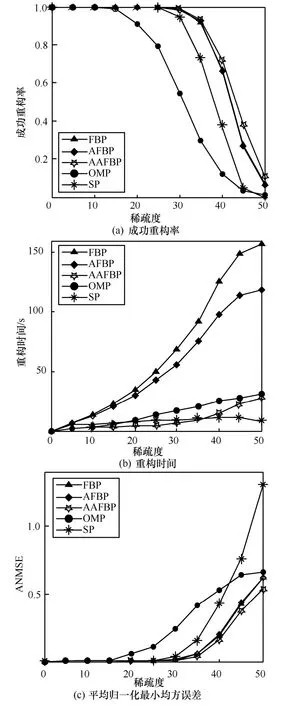
图4 均匀稀疏信号重构结果比较

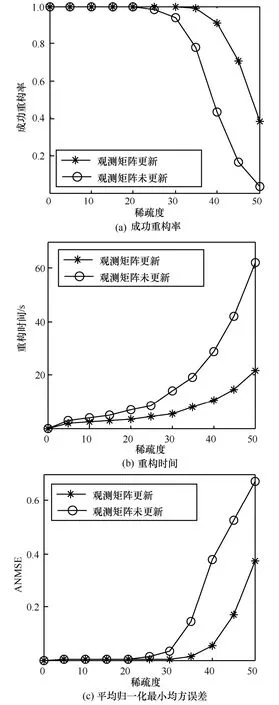
图5 观测矩阵更新与否对重构结果的影响

3)为了进一步地分析回溯过度现象对于重构结果的影响，图5 给出AAFBP 算法是否进行观测矩阵更新操作所对应的不同稀疏度下的成功重构率、重构时间和ANMSE 值。其中实验参数与上述一致，观测矩阵为Gauss 随机矩阵。从图5 中可以看出，回溯过度问题对算法的成功重构率从K＞25后产生了较大的影响。由图1 中可知，K＞25 后正确原子开始被删除。同时随着稀疏度增加，由于回溯过度现象，重构过程中算法的残差值难以低于设定的停止阈值，回溯的迭代过程依靠设定的迭代次数上限来停止，导致回溯时间延长。从ANMSE 值中也可以看出，当K＞25 后，算法未进行观测矩阵更新操作将产生更大的误差。因此AAFBP 进行观测矩阵的更新操作能够有效避免回溯过度问题。

4.3 二维图像重构

为了进一步验证AAFBP 算法对实际非零稀疏分布信号的重构性能，选用256×256的‘Lena’图像进行压缩重构实验[20]。其中实验过程设置与文献[12]保持一致，即将图像分割成8×8 的小块，将复杂的问题分解成一个个简单的小部分。对于分割出来的小块，令其在haar 小波基上稀疏度为K，即保证转换到小波域时，仅保留K个较大的小波系数，其中K=12。对于每个分块，信号长度为N=64，测量值M=32，即压缩比为0.5。观测矩阵ΦN×M是均值为0、方差为的高斯矩阵，并归一化每一列。FBP 和AFBP 算法的前向后向步长一致，设置为α=10，β=9。AFBP 算法的权重设置为w1=2.0，w2=1.5，w3=1.0；阈值设置为η1=5，η2=6，η3=7。本文提出的AAFBP 算法的模糊参数设置为a=0.4，μ2=0.8。其中‘Lena’图像的重构结果如图6 所示。

图6 ‘Lena’原图像及各算法重构图像

用峰值信噪比（PSNR,peak signal to noise ratio）和均方误差（MSE,mean squared error）来进行图像重构质量的判别，其中各算法的PSNR、MSE和重构时间如表1 所示。从表1 中可以看出，当压缩比为0.5 时，AAFBP 算法重构效果最佳，PSNR值达到28.99 dB。重构时间低于AFBP 和FBP 算法的时间。因此AAFBP 算法有能力在保证重构质量的基础上，减少重构所需的时间。

5 结束语

为了提升FBP 算法的运算效率，本文在AFBP算法的基础上，提出了AAFBP 算法。该算法对AFBP算法在前向阶段固定选入大量原子的操作进行改进，通过模糊参数自适应地选取合适数量的原子加入支撑集。在后向阶段中以原子的投影系数大小作为其是否进行删除的判别准则，避免AFBP算法中依赖权重作为判别准则所引入的误差。同时，通过对观测矩阵内容进行及时更新，来解决回溯过程中存在的回溯过度现象，提升了算法的重构精度。仿真实验结果表明，AAFBP 算法在每次迭代过程中能够保留更多正确的原子，因此该算法可以实现在提升重构质量的同时，降低算法的运行时间。

表1 压缩比为0.5 时各算法重构质量及重构时间对比