基于编码的多接收方广义签密方案

韩益亮，王众

（武警工程大学密码工程学院，陕西 西安 710086）

1 引言

公钥密码技术是网络通信安全的核心技术，当前常用的公钥密码方案基于整数分解、离散对数、椭圆曲线离散对数等困难问题。Shor[1]提出了一种可以在量子计算机上运行的算法，能够解决整数分解、离散对数等问题，这给传统公钥密码带来了严重威胁，一旦实用化量子计算机出现，传统公钥密码就不再安全。整数分解和离散对数等问题都可归结为交换群的隐含子群问题，这类问题在量子计算机上可在多项式时间内求解，而在经典计算机上最好的算法仍然是指数级的。目前，一般认为抗量子计算攻击的密码体制有如下几种[2]：基于多变量的密码体制[3]、基于格的密码体制[4]、基于编码的密码体制[5]以及基于Hash 函数的密码体制[6]等。这些密码体制之所以能够抵抗量子计算攻击，是因为它们建立在NP 完全问题（NP-complete problem）之上，量子计算机相比经典计算机对此类问题并没有明显优势[7]。基于编码的密码是目前比较受关注的一种抗量子密码，所依赖的困难问题是一般线性码的译码问题，主要思路是向码字中加入错误向量或根据纠错码的校验矩阵计算伴随式，在生成矩阵或校验矩阵未知时该问题为NP 完全问题，且尚未发现该问题能归结为隐含子群问题，因而可以作为抗量子公钥算法比较好的候选方案之一。1978 年，Mceliece[8]最早利用Goppa 码的性质提出了第一个编码密码方案，通常被称为McEliece 方案。1986年，Niederreiter[9]提出了McEliece 方案的对偶体制，即Niederreiter 方案。上述2 种方案在安全性上完全等价，但是Niederreiter 方案相比McEliece 方案具有更高的传信率。2001 年，Courtois 等[10]提出了基于编码密码的签名方案——CFS 方案。2013 年，Mathew 等[11]通过密钥构造的改变使CFS 签名方案的密钥量减少，提高了签名方案的使用效率。为了解决编码密码密钥量大的问题，用其他码字来代替Goppa 码已经成为一种趋势，但是这会对方案的安全造成影响，这种影响已经出现在基于准循环（QC,quasi-cyclic）码[12]、低密度奇偶校验（LDPC,low density parity check）码[13]、准循环低密度奇偶校验（QC-LDPC,quasi-cyclic low-density parity-check）码[14]、卷积码[15]等码字的第一代McEliece 变体方案中。还有一些使用QC-LDPC 码[16]、准循环中密度奇偶校验（QC-MDPC,quasi-cyclic medium-density parity-check）码[17]等码字的变体方案，能够在不损坏安全性的前提下较好地达到密钥压缩的目的，例如2017 年Deneuville 等[18]提出的Ouroboros 密钥交换协议、2018 年Baldi 等[19]提出的LEDAkem 密钥封装机制等。2018 年，Eaton等[20]还提出通过多次加密的方式使编码密码方案的安全性达到IND-CCA2（indistinguishability under adaptive chosen-ciphertext attack）的安全级别。

另一方面，保密和认证是信息安全的2 个主要目标，在公钥密码领域，通常用加密技术来实现保密，用数字签名来实现认证。当需要同时满足保密和认证的要求时，通常的做法是先“签名”再“加密”或者先“加密”再“签名”，但这种方法效率不高，同时也无法确保安全性。Zheng[21]提出了在一个逻辑步骤内同时实现加密与签名功能的密码技术，能够提高效率和安全性。当系统中同时存在多种安全需求时，韩益亮等[22]提出的广义签密能够在签名方案、加密方案以及签密方案三者之间自适应地转换，能够单独或者同时提供保密和认证功能，更有效地节省系统资源。公钥密码是签密技术的基础，但是公钥密码存在一类密钥托管问题。2003 年，Al-Riyami 等[23]首次提出无证书密码体制，该体制的重点为密钥的管理，其将用户的私钥分成两部分：一部分由密钥生成中心（KGC,key generator center）生成，另一部分则由用户生成，这样就缓解了密钥托管问题。2008 年，Barbosa 等[24]将签密与无证书密码体制相结合，使无证书密码体制可以在一个逻辑步骤内完成加密与签名操作。同年，Selvi 等[25]将无证书签密方案推广到多接收者模型中。目前，已经提出的各种签密方案大多基于整数分解、离散对数、椭圆曲线离散对数等困难问题，也不能抵抗量子计算攻击。

本文通过对编码密码进行研究，设计了一个多接收方的广义签密方案。首先采用QC-LDPC 码借鉴文献[20]中密钥封装机制中的加密方法，提出一种能够满足IND-CCA2 的加密方案，在加密方案的基础上设计了一个多接收方的签密方案；然后进行改进得到一个基于编码密码的广义签密方案。

2 相关知识

2.1 校验子译码问题

给定一个(n,k)维的线性码，已知该码的最小汉明距离为d，其校验矩阵为，纠错能力为t，满足d=2t+1。给定向量，寻找一个错误向量，使其汉明重量满足wt(e)≤t，且与向量v以及矩阵H满足方程v=eHT，寻找错误向量e的问题即为校验子译码问题（SD,syndrome decoding problem）。

校验子译码问题已被证明是NP 完全问题，尚未发现该问题能归结为隐含子群问题。该问题是基于编码的密码所依赖的困难问题。

2.2 Mceliece 方案

Mceliece[8]于1978 年提出一个基于Goppa 码的密码方案，该方案是第一个基于编码的加密方案。目前，采用Goppa 码的McEliece 方案仍是较为安全的方案。下面将具体介绍该方案的参数生成以及加解密过程。

参数生成。选择一个(n,k)维的线性码，该码的最小汉明距离为d，其生成矩阵为，能纠错重量为t的信息，满足d=2t+1。选择一个k×k阶的二元随机非奇异矩阵M和一个n×n阶的二元随机置换矩阵P。那么，该方案的公钥为重量t以及矩阵Gpub=MGP，私钥为矩阵G、M、P以及译码算法β。

解密过程。首先对密文c右乘置换矩阵P的逆，即cP-1=mMG+eP-1。对cP-1进行译码操作消除错误向量eP-1，进而得到右乘私钥矩阵M的逆即可得明文m。

2.3 CFS 签名方案

基于McEliece 方案，2001 年Courtois 等[10]提出CFS 签名方案，该方案是目前为数不多的安全的编码签名方案。CFS 签名方案的初始化、签名与验证过程如下。

初始化过程。取C是有限域GFq上线性(n,k,d)Goppa 码，n=2a，d=2t+1，k=n-at。(n-k)×n阶矩阵H为二元(n,k,d)Goppa 码的校验矩阵，随机选取GF(2)上的可逆矩阵S，其阶为(n-k)×(n-k)，再选取置换矩阵T，其阶为n×n。选择一个散列函数。Goppa 码的快速译码算法为βHt()，σ为待签名消息。将公开，将(S,T,H,βHt())保密。

签名过程如下。

1)计算σ的散列值m，m=h(σ)。

2)在集合{0,1,2,…} 中选择一个i，计算mi=S-h1(m||i)，找到一个最小的i0使βHt(mi)存在，则mi0=S-1h(m||i0)。

3)令v=βHt(mi0)，签名即为 (i0||vT)。

验证过程如下。

1)计算a=h(h(σ)||i0)，。

2)如果a=b，则签名成功；否则失败。

2.4 多接收方签密与广义签密

根据文献[26]，多接收方签密方案由以下步骤组成：系统参数生成、部分密钥生成、用户密钥生成、签密过程和解签密过程。

1)系统参数生成。由密钥生成中心（KGC）进行，输入一个秘密参数φ，进而返回系统参数τ。

2)部分密钥生成。由KGC 进行，KGC 首先产生系统密钥λ，然后输入λ和τ，产生部分公钥P和部分私钥S。

3)用户密钥生成。输入公共参数τ、部分公钥P、部分私钥S以及用户的身份信息IDU，用户U执行该算法产生自己的公钥PU和私钥SU。

4)签密过程。由发送方A执行，输入公共参数τ、明文m、A的身份信息IDA、私钥SA以及接收者组L的公钥信息，最终输出签密文c。

5)解签密过程。由接收者B执行，输入公共参数τ、签密文c、A的身份信息IDA、A的公钥PA，以及接收者B的身份信息IDB与私钥SB，若验证通过则最终解密得到明文m，否则解签密失败。

多接收方的广义签密与多接收方的签密过程大致类似，不同之处在于需要再定义一个区分函数f(x)来实现签名方案、加密方案以及签密方案这三者之间的转换。区分函数往往通过用户的公钥进行判断，进而实现转换的功能，具体来讲即当发送方A与接收者B均有公私钥时为签密方案，当发送方A没有公私钥而接收者B拥有时为加密方案，当接收者B没有公私钥而发送方A拥有时为签名方案，当收发双方均无公私钥时为普通的传信过程。

2.5 多接收方签密的安全模型

参考文献[26-27]可以得到适用于本文多接收方签密方案的安全模型。从机密性与不可伪造性入手，针对多接收方的签密方案，存在以下2 种类型的攻击者：可以替换用户公钥信息但是不能获得KGC 的主密钥，用攻击者α1表示；可以获取KGC的主密钥但是不能替换其他用户公钥的攻击者，用α2表示。

定义1机密性1。在攻击游戏1 中，没有一个攻击者α能够在多项式时间内以不可忽略的优势赢得IND-CCA2-1 游戏，则说明该基于编码的多接收方签密方案满足适应性选择密文攻击下的不可区分性。

攻击者在IND-CCA2-1 游戏中需满足以下3个限制：不能对挑战密文进行解签密询问，不能对挑战者的私钥进行询问，不能对系统的主密钥进行询问。

定义2机密性2。在攻击游戏2 中，没有一个攻击者α能够在多项式时间内以不可忽略的优势赢得IND-CCA2-2 游戏，则说明该基于编码的多接收方签密方案满足适应性选择密文攻击下的不可区分性。

攻击者在IND-CCA2-2 游戏中需要满足以下3 个限制：不能对挑战密文进行解签密询问，不能对挑战者的私钥进行询问，不能对系统的主密钥进行替换。

定义3不可伪造性1。在攻击游戏1 中，没有一个攻击者α能够在多项式时间内以不可忽略的优势赢得EUF-CMA（existential unforgeability against adaptive chosen messages attack）-1 游戏，则说明该基于编码的多接收方签密方案满足适应性选择消息攻击下的不可伪造性。

攻击者在EUF-CMA-1 游戏中需满足以下2 个限制：不能对挑战者的私钥进行询问，不能对系统的主密钥进行询问。

定义4不可伪造性2。在攻击游戏2 中，没有一个攻击者α能够在多项式时间内以不可忽略的优势赢得EUF-CMA-2 游戏，则说明该基于编码的多接收方签密方案满足适应性选择消息攻击下的不可伪造性。

攻击者在EUF-CMA-2 游戏中需满足以下2 个限制：不能对挑战者的私钥进行询问，不能对系统的主密钥进行替换。

3 方案描述

3.1 多接收方的通信模型

具有多个接收方的一对多通信是当前最普遍的通信模式之一，如网络广播、多播等。在无线局域、物联网等网络环境下，也存在着许多一对多通信的方式。这种具有多个接收方的一对多通信由于其自身的开放性、智能化以及计算环境的复杂性带来了许多安全问题，最明显的是用户隐私的安全问题[28]。多接收方通信中的身份认证问题同样重要，通过有效的消息认证、设备认证，才能够防止冒名顶替和否认行为[29]。计算机系统需要根据不同用户的性质来提供不同的访问控制策略以有效地对用户隐私、数据安全以及身份进行保护。图1 为多接收方通信模型。

1)当发送方无密钥以及接收用户组存在无密钥成员时，发送方将不能对待签密消息m进行签名以及加密的操作，相当于直接把消息发送给接收用户组。由于对明文进行了处理，使合法的系统用户（设备）才能得到明文m。这种情况适用于普通用户（设备），即没有自己公私钥的用户（设备）与普通的用户或者设备组之间进行密级较低的通信，传输的信息对于系统用户（设备）是公开的，而对于非系统用户（设备）是加密的。

2)当发送方有密钥而接收用户组存在无密钥成员时，相当于纯签名的过程。当接收用户组收到该信息后，可以利用系统私钥来解密得到明文m，再对签名s验证，确保信息来自对应的发送方且明文未被篡改。这种情况适用于发送方是高级的用户、计算机系统或者设备，而接收组是普通的用户或者设备，进而防止对高级用户（设备）所传输的信息进行篡改，以及对其冒名顶替，保障了可认证性。

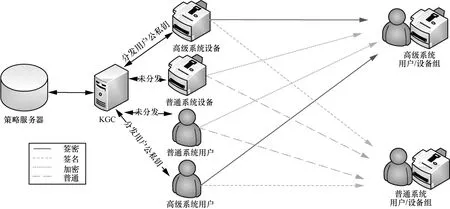
图1 多接收方通信模型

3)当发送方没有密钥而接收用户组中的成员均有密钥时，相当于纯加密的过程。接收组收到该信息后利用各自的私钥以及系统私钥进行解密操作即可得到明文消息m。这种情况适用于发送方为普通用户或者计算机系统，其所发出的消息只想让指定的接收组收到，且接收方为高级的用户或者设备。这就保障了在多接收方的开放环境下数据传输的机密性。

4)当接收用户组中的成员、发送方都有各自密钥时，该方案即为一个签密方案。只有拥有相应私钥的接收者可以对信息进行解签密。解签密的过程是接收组中的成员运用自己的私钥以及系统私钥进行解密得到明文，再利用发送方的公钥通过m对签名进行验证。这种情况适用于收发双方均为高级的用户、设备，进行密级较高的保密通信。

综上分析可知，当一个系统用户或者设备给其他多个接收者发送信息时，可以根据接收组成员的公私钥的存在情况自适应地实现多接收方的签密、加密与签名的转换。若接收组成员中有一个没有公钥即为签名过程或者是普通传输过程，若接收组成员中都有公钥即为签密或者加密的传输过程。本文所提广义签密方案需要实现不同安全级别的访问控制，而非系统用户则得不到任何信息。

3.2 多次加密的McEliece 方案

根据文献[20]，一般编码密码方案的安全性达不到IND-CCA2 的安全级别，但文献[20]给出了一种加密方法使编码密码的安全性能够达到IND-CCA2 的安全级别。该加密方法是将待加密信息运用编码加密的方式进行多次加密产生多个密文，对这些密文进行解密，只有当这些密文全部解密失败时返回错误值⊥，这样可以有效避免译码错误对安全性的影响。本节多次加密的McEliece 方案采用QC-LDPC 码，并以这种多次加密的方式来构造方案，以增加方案的安全性。

参数及密钥生成。取Ω是有限域GFq上 (n,k,d)阶的QC-LDPC 码，n=2a，d=2t+1，k=n-at。其生成矩阵为，随机选取GF(2)上的可逆矩阵S，其阶为k×k；再选取置换矩阵P，其阶为n×n。计算公钥为=SGP，私钥即为矩阵(S,G,P)以及译码算法βt()。另设一错误向量生成函数以及二进制数字的循环左移函数。

根据文献[20]密钥封装中的加密方式，基于QC-LDPC 码构造多次加密的McEliece 方案。

加密过程中，每加密一次产生一个新的错误向量ei来加密。解密过程中，需要对所有密文进行解密操作，译码成功则保留下来，所有密文译码不成功则解密失败，最终得到明文，根据明文m以及公钥并利用之前的加密算法进行加密操作，得到一组密文来与原密文组C进行比较，每组都相同则解密成功，可以得到明文m。这种加密方法大大降低了译码错误所带来的安全性影响，这也是本文构造多次加密的McEliece 方案最主要的原因。

3.3 多接收方签密方案

本节将依托3.2 节中的多次加密的McEliece 方案以及CFS 签名方案并参考文献[26]，构造一个具有抗量子计算能力的多接收方签密方案。

1)系统参数建立

取Ω是有限域GFq上 (n,k,d)阶的QC-LDPC码，n=2a，d=2t+1，k=n-at。其生成矩阵为，校验矩阵为，译码算法为βt()。设置 2 个安全函数h1与h2，h1:{0,1}*→{0,1}n-k，h2:{0,1}*→{0,1}k。如3.2 节中方案的参数及密钥生成过程，再设置错误向量生成函数X:{0,1}*→{e|e∈,wt(e)≤t} 以及二进制数字的循环左移函数PRF。公开(n,k,t,h1,h2)。

2)部分密钥生成

①KGC 根据QC-LDPC 码Ω随机选择GF(2)上的k×k阶可逆矩阵S，以及(n-k)×(n-k)阶可逆矩阵M，再选取n×n阶置换矩阵P。KGC 的系统公钥为Gpub=SGP和Hpub=MHP，Gpub与加密有关，Hpub与签名有关。系统私钥为(S,G,P,M,βt())，这里不再将QC-LDPC 码的校验矩阵H写入私钥组，因为根据码的性质，有了生成矩阵便可根据GHT=0求得校验矩阵。

② KGC 根据QC-LDPC 码Ω随机选择GF(2)上的k×k阶可逆矩阵S0，以及(n-k)×(n-k)阶可逆矩阵M0，再选取n×n阶置换矩阵P0。计算G0=S0GpubP0，H0=M0HpubP0，则部分公钥为(G0,H0)，部分私钥为(S0S,G,PP0,M0M,βt())。KGC 通过秘密信道将部分私钥传递给合法用户，并公开自己的系统公钥。

3)用户密钥生成

①用户U取得KGC 的部分公钥和部分私钥，并随机选择GF(2)上的k×k阶可逆矩阵SU，以及(n-k)×(n-k)阶可逆矩阵MU，再选取n×n阶置换矩阵PU。计算GU=SUG0PU，HU=MUH0PU，则部分公钥为 (GU,HU)，部分私钥为(SUS0S,G,PP0PU,MUM0M,βt())。F0代表采用系统公钥加密,Fi代表采用用户i的公钥加密。

② 用户U将公钥FU（FU即为(GU,HU)）传回KGC。

4)签密

身份为IDA的用户A，将传输给用户组L={ID1,ID2,…,IDς}。首先向KGC 查询得到用户组L的公钥信息，进行如下操作。

②Y=h1(m||IDA||x)。

③在集合{0,1,…} 中选择一个a，并计算，找到一个最小的a0使βt(Ya)存在，则

④令v=βt(Ya0)，s=(a0||vPA)。

⑤对于IDi，i=1,2,…,ς，计算qi=h2(IDi)。

⑥Wi=Fi(m⊕r⊕qi)。

⑦对于用户组L，计算=F0(L)。

⑧ 生成签密文σ=(s,W1,W2,…,Wς,,x)。

5)解签密

用户IDi，i=1,2,…,ς，收到σ=(s,W1,W2,…,Wς,,x)后进行如下计算。

正确性分析。当签密与解签密过程正确时则说明签密方案正确。用户IDi(i=1,2,…,ς)收到σ=(s,W1,W2,…,Wς,,x)后，首先利用系统私钥提取出自己的那一部分密文，再利用系统私钥求解出随机数，然后就可以利用自己的私钥来求解密文，即。由于已知、c和qi，因此可以求出明文。拥有了明文后，可运用发送方A的公钥进行下一步的验证，根据CFS签名方案，当且仅当时，才可得到正确的明文。

3.4 基于编码密码的多接收方广义签密方案

本节基于编码密码的多接收方广义签密方案仍然是依托3.2 节中多次加密的McEliece 方案以及CFS 签名方案，在3.3 节基于编码密码的多接收方签密方案的基础上加以改进而构造的，因此其参数、部分密钥以及用户密钥的生成都与3.3 节中基本相同，只是在参数生成时多构造一个安全函数h3:{0,1}*→{0,1}k。

3.4.1 区分函数构造以及签密与解签密过程

1)定义区分函数f(x)

区分函数实现签名、加密或签密功能三者之间转换，往往以用户是否存在公钥来进行判断。当用户的公钥GU=∅时即为不存在公私钥，则f(x)=0，此处0 代表k维零向量；当用户的公钥GU≠∅时即存在公私钥时，则f(x)=1，此处1代表k维单位向量。因此区分函数可表示如下。

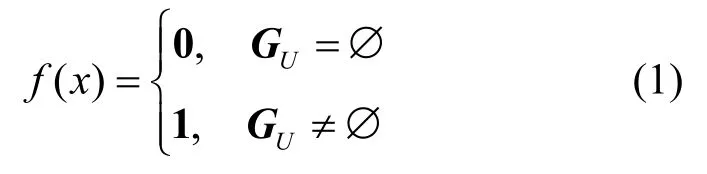
2)签密

身份为IDA的用户A，将m∈F2k传输给用户组L={ID1,ID2,…,IDς}。首先向KGC 查询得到用户组L的公钥信息，进行如下操作。

3)解签密

判断η与ξ是否相等，相等则验证通过获得正确明文，否则接收失败。

3.4.2 正确性分析

当用户IDi(i=1,2,…,ς)收到σ=(s,W1,W2,…,Wς,c1,c2,…,cς,,x)后，最终得到的密文组有以下4种形式：(s,Wi,ci,x)、(∅,Wi,ci,x)、(s,m⊕h3(r),ri,x)、(∅,m⊕h3(r),ri,x)。

当收发双方都拥有公私钥时，密文组为(s,Wi,ci,x)。接收者利用自己的私钥解密得到随机数，利用系统私钥进行解密得到随机数，进而可以利用求解得出明文，将该明文利用CFS 签名方案中的验证方法进行验证：等式成立则说明获得了正确的信息。

当发送方没有公私钥而接收方有时，密文组为(∅,Wi,ci,x)，接收方收到密文组后，利用自己的私钥进行解密得到随机数，利用系统私钥进行解密得到随机数，再利用求解得出明文。

当发送方拥有公私钥而接收方不具有时即为签名方案，不同于普通签名，只有系统中的合法用户才可以得到正确的信息，此时的密文组为(s,m⊕h3(r),ri,x)，接收方收到密文后，可以直接获取随机数，再利用系统私钥进行解密得到随机数，进而可以利用求解得出明文，最后利用与第一种情况相同的方法进行验证即可。

当收发双方均无公私钥时，相对于直接传输明文，发送方只对明文用系统公钥进行了加密，当接收方为系统用户时，便可利用系统私钥进行解密最终获得明文。

3.5 广义签密方案自适应性

根据多接收方广义签密的模型[30]并结合上述方案的构造可以看出，当发送方向某一用户组发送信息时，根据发送方以及接收用户组的密钥拥有情况存在以下4 种情况。

1)发送方以及接收用户组均无密钥。根据3.4节中的签密过程可以看出，签密的步骤②即签名过程将不再进行，而步骤⑤所得的Wi即为m⊕h3(r)，说明合法的系统用户作为接收方可以直接得到明文。这种情况下，合法的系统用户均无自己的密钥，也即普通系统设备与用户之间进行的一般的通信过程。这种过程与3.1 节所设计的多接收方通信模型的第一种情况相适应。

2)发送方有密钥，而接收用户组中存在没有密钥的成员。此时，根据3.4 节中的签密过程可以看出，签密的步骤②即签名过程将进行，但是由于接收用户组中存在无密钥成员，因此κ=f(G1)f(G2)…f(Gς-1)f(Gς)=0，步骤⑤所得的Wi即为m⊕h3(r)。说明签名功能得到实现但未进行加密，合法的系统接收用户均可以对发送方的签名进行验证，并得到明文。这种安排是根据文献[30]中提到的安全性，防止发送方向用户组发送信息时，存在有的用户得到加密后的信息，而有的用户得到未加密信息，造成明密文对比，使攻击者可以进行分析而造成漏洞。这种情况与3.1 节所设计的通信模型的第二种情况相适应，即高级的系统用户或者设备向存在普通用户或设备的接收用户、设备组传输信息，接收组可以对信息来源以及信息是否被篡改进行确认。

3)发送方没有密钥，而接收用户组中的成员均有密钥。根据3.4 节中对签密过程的描述可以看出，签密的步骤②即签名的过程将跳过，但是由于接收用户组成员均有密钥，因此Wi=m⊕h3(r)⊕h2(ri⊕qi)，只有接收用户组中的第i个成员使用自己的密钥，才可以对Wi=m⊕h3(r)⊕h2(ri⊕qi)进行正确解密，再利用系统密钥处理得到明文。这种情况与3.1 节中通信模型的第三种情况相适应，普通系统用户或者设备向高级的接收用户、设备组发送信息，只有该接收用户、设备组能够对信息进行正确解密，得到对应的明文。

4)发送方以及接收用户组均有密钥。3.4 节中的全部过程将进行，即签密功能的实现。这种情况与3.1 节通信模型的第四种情况相适应，高级的系统用户或设备与另一组高级的用户、设备进行高安全级别的通信。

综上所述，3.4 节所设计的多接收方广义签密方案可以与3.1 节所设计的多接收方通信模型相适应。

4 安全性分析

本文多接收方的签密以及广义签密方案是一脉相承的，因此第4 节的安全性分析主要是从广义签密方案出发，对具有签密功能的广义签密方案入手，分析方案的机密性以及不可伪造性，证明过程在文献[26-27,31]的基础上进行。

4.1 机密性

1)游戏类型1

定理1 在随机预言机模型下，假设存在一个IND-CCA2 的攻击者α1，能够以优势赢得如下定义的游戏（定义1 中的游戏），那么就存在一个算法β，它解决SD 问题的优势ε如式(2)所示，其中算法β作为攻击者α1在游戏中的挑战者，而α1则作为β的子程序。

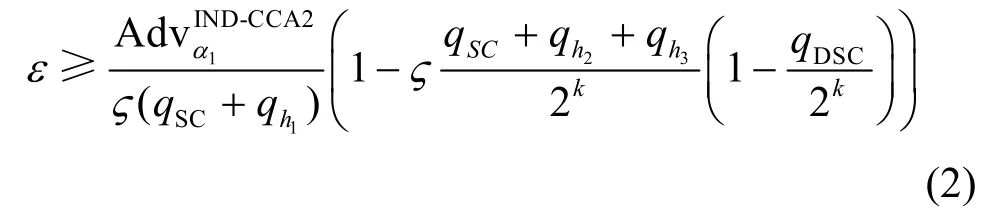
证明给定一个SD 问题实例x=F(r)，挑战者成功求解出r即可。

qSC、qDSC、qh1、qh2、qh3分别代表攻击者α1所能进行的签密询问、解签密询问，以及对随机预言机h1、h2以及h3的询问的最大次数，qS、qP、qR分别代表私钥询问、公钥询问以及公钥替换询问的最大次数。为了方便回答询问，并设立2 个询问列表List1、List2，来对以上询问进行记录。

①游戏初始化。β根据QC-LDPC 码Ω随机选择 GF(2)上的k×k阶可逆矩阵S和(n-k)×(n-k)可逆矩阵M，选取n×n阶置换矩阵P。KGC的系统公钥为Gpub=SGP和Hpub=MGP，系统私钥为(S,G,P,M,βt())，根据QC-LDPC 码Ω随机选择GF(2)上的k×k阶可逆矩阵S0和(n-k)×(n-k)阶可逆矩阵M0，选取n×n阶置换矩阵P0。计算G0=S0GpubP0，H0=M0HpubP0，则部分公钥为(G0,H0)，部分私钥为(S0S,G,PP0,M0M,βt())。β将公共参数(n,k,t,h1,h2,h3)发送给攻击者α1，并保留自己的系统密钥。攻击者α1给出目标用户组

② 询问阶段。攻击者α1可以向挑战者β进行如下询问。

h1询问。输入元组，查看表List1，如果存在相应记录Yi则返回该记录；若不存在则随机选取一个Yi，将其以及用户对信息m签密产生的密文与签名存入表List1，并返回Yi。

2h询问。有以下几种情况。输入进行询问时，对表List2进行查询是否有相应记录qi，存在则返回，不存在则随机选择一个qi存入List2，并将用户的公钥、私钥以及一个记录用户公钥是否被替换的标识ϖ（ϖ=0表示未被替换，ϖ=1表示被替换）一同记录下来，返回qi。输入(ri,qi)进行询问，同样先对表 List2进行查询是否有相应记录，存在则返回，该记录存在的概率很小，为，不存在则随机选择一个记录在List2，并将用户的公钥、私钥以及一个记录用户公钥是否被替换的标识ϖ一同记录下来，返回

h3询问。输入随机数r询问时，返回值如果存在相应记录，则返回，但这种概率存在的可能极小，为。因为是对随机数查询，所以查询过的概率很小。

私钥询问。攻击者输入用户IDi，若该用户存在于目标用户组中，则挑战者β丢弃该询问；否则，β查找List2。首先查看该用户的替换标识ϖ检查其公钥是否被替换，若未被替换，则返回该用户私钥(SiS0S,G,PP0Pi,MiM0M,βt())；若被替换，则β向α1询问用户IDi的私钥参数。最终返回攻击者(SiS0S,G,PP0Pi,MiM0M,βt())。

公钥询问。攻击者输入用户IDi，首先查询List2中是否有相应记录，存在则返回Fi；否则选择随机矩阵(Si,Pi,Mi)，并进行相应计算产生对应公钥Fi。把该值更新记录到表List2中并返回。

公钥替换询问。输入二元组(IDi,)进行询问，首先查询List2，若存在记录(IDi,Fi)，则使用替换Fi，并更新标识ϖ；若没有对应公钥，则对IDi进行公钥询问，得到新公钥后，再进行替换询问。

签密询问。输入元组(m,IDs,L={IDR1,IDR2,…,IDRς})，若IDs存在于身份集合L中，或L中有元素存在于目标身份集合L*中，β丢弃此次询问；若IDs不在目标身份集合L*中，则可以知道发送方的私钥，并在List1、List2中记录。进行本文的签密算法，得到相应的签密文σ=(s,W1,W2,…,Wς,c1,c2,…,cς,,x)。如果在目标身份集合中，则挑战者无法获知发送方的私钥，可通过以下方法来进行签密：β询问List2，得到IDs的公私钥，选择随机数r用公钥加密得到FS(r)→x，再进行h1询问以及签名算法得到签名s。β随机选择qi，对List2进行查询得到记录(IDRi,ϖRi)，首先查看替换标识，检查公钥是否被替换，未被替换则进行h2询问以及加密算法，得到密文Wi与用户组标识；否则进行公钥替换询问与公钥询问，并将该记录存入表List2，若表List2中已经存在了相应记录则说明模拟签密失败。由β返回给攻击者α1签密文。模拟签密失败的概率为

解签密询问。输入签密文σ，发送方以及接收者身份IDS、IDR。首先提取出对应接收者的签密文(s,Wi,,ci,x)，若该接收者属于目标用户组，则β知道该接收者的私钥，便可进行解密算法求出明文；否则需要查看List1中是否有该签名s以及密文iW的记录，若没有相应记录则β拒绝该签密文。再看表List2，若没有关于接收者IDR的用户标识、公私钥、替换标识的记录，β也拒绝该签密文。当对密文解密时，运用系统私钥以及接收者私钥进行解密得到明文m，利用签名验证算法与该信息m对签名s进行验证，当且仅当签名验证成功时，可获得正确明文m，否则解签密失败。一个有效的密文被拒绝的概率为。

③挑战阶段。攻击者α1提供2 个k维的消息1m、m2以及发送方IDS，且发送方不在目标用户身份集合L*中，向β进行询问。β选择一个消息mb，其中b∈{0,1}，并发送给目标用户组。β进行如下操作进而利用CFS 算法产生签名s*。产生签名后，由β产生相应的密文，具体方法如下：由β进行操作，得到密文，最终的签密文为

④询问阶段。攻击者α1仍可进行如阶段②的询问，但是不能为接收者向挑战密文σ*进行询问。

⑤猜测阶段。α1输出1 bit作为猜测。如上所述，若α1猜测成功，那么必须通过h1询问得到密文，β在List1中随机选择一个记录且包含正确签名、密文的概率为。最后将β输出的r,ri作为SD 问题的解。

根据以上分析，β成功即攻击者α1输出正确比特的概率需要考虑以下几个因素。首先设攻击者α1成功这件事为E，其概率为。设E1表示挑战者对目标用户组中的私钥进行询问，E2表示发送方以及存在一个接收者属于目标用户组，若这2 个事件发生，β自动放弃此次询问；E3表示挑战者β在进行h2询问时，List2中的相应记录出现了碰撞情况，则签密模拟失败，其概率为。E4表示一个有效签名被拒绝，其概率为。E5表示β在表List1中随机选择一个记录且包含了正确元素，其概率为。所以概率为Pr[E ∩ E1∩E2∩E3∩ E4∩E5]。β成功解决SD 问题的优势ε为

定理1 证毕。

2)游戏类型2

定理2在随机预言机模型下，假定存在一个IND-CCA2 的攻击者α2，它能够以优势赢得定义2 中的游戏，那么就存在一个算法β，它解决SD 问题的优势ε如式(3)所示，其中算法β作为攻击者α2在游戏中的挑战者，而α2则作为β的子程序。

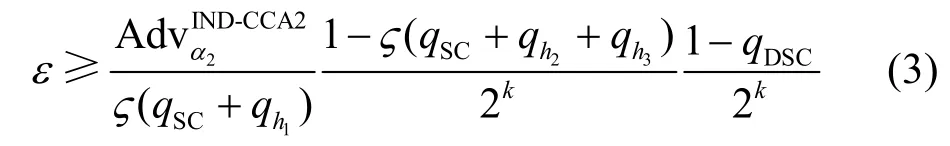
证明在游戏类型2 中，不同于游戏类型1，攻击者α2可以获得系统主密钥信息，但是不能对用户的公钥进行替换，对于定理2 的证明与定理1 的证明类似，易得定理2 成立。证毕。

4.2 不可伪造性

1)游戏类型1

定理3在随机预言机模型下，假设存在一个EUF-CMA 的攻击者α1，它能够以优势赢得如下定义的游戏（定义3 中的游戏），那么就存在一个算法β，它解决SD 问题的优势υ如式(4)所示，其中算法β作为攻击者α1在游戏中的挑战者，而α1则作为β的子程序。

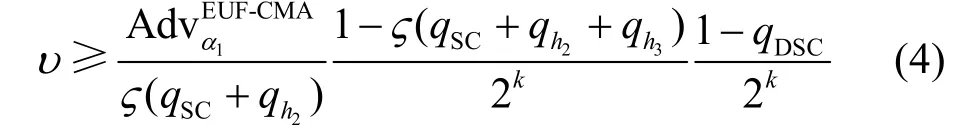
证明给定一个编码密码中的问题实例(HS=MSH0PS,H0)，β需要求出MS,PS。

①游戏初始化。同4.1 节中游戏类型1 中的①。

②询问阶段。与4.1 节中游戏类型1 中的②相似，不同之处在于最后的解签密询问换为了验证询问，具体询问过程如下。输入签密文σ、发送方身份IDS、接收者身份IDR。首先提取出对应接收者的签密文，若该接收者属于目标用户组，则β知道该接收者的私钥，可以进行解密算法求出明文，否则需要查看List1中是否有该签名s以及用户组的记录，若没有相应记录则β拒绝该签密文。若List2中没有关于接收者IDR的用户标识、公私钥、替换标识的记录，β也拒绝该签密文。当对密文解密时，运用系统私钥以及接收者私钥进行解密得到明文m，利用签名验证算法与该信息m对签名s进行验证。一个有效的密文被拒绝的概率为。

③伪造阶段。攻击者α1输出伪造的签密文，其中发送方IDS是属于目标身份用户组L*的，接收者IDRi中至少有一个是属于L*的。

通过上述的分析可知，若攻击者α1伪造签密文成功，需要通过h2询问得到发送方IDS的私钥MS,PS，β需要在List2中随机选择一个记录且包含了正确元素MS,PS，概率为。将正确记录中的MS,PS作 为β对问题实例(HS=MSH0PS,H0)的求解。设攻击者α1伪造的签名σ*通过验证这件事为 E，其概率为。设E1表示挑战者对目标用户组中的私钥进行询问，设E2表示发送方以及存在一个接收者属于目标用户组中，若这2 个事件发生β会自动放弃此次询问。设E3表示挑战者β在进行h2询问时，List2中的相应记录出现了碰撞情况，则签密模拟失败，其概率为。设E4表示一个有效签名被拒绝，其概率为。设E5表示β在表List1中随机选择一个记录且包含了正确元素，其概率为。所以概率为Pr[E ∩ E1∩ E2∩ E3∩ E4∩E5]。β解决SD 问题的优势υ为

证毕。

2)游戏类型2

定理4在随机预言机模型下，假设存在一个EUF-CMA 的攻击者α2，它能够以优势赢得如下定义的游戏（定义4 中的游戏），那么就存在一个算法β，它解决SD 问题的优势υ如式(5)所示，其中算法β作为攻击者α2在游戏中的挑战者，而α2则作为β的子程序。

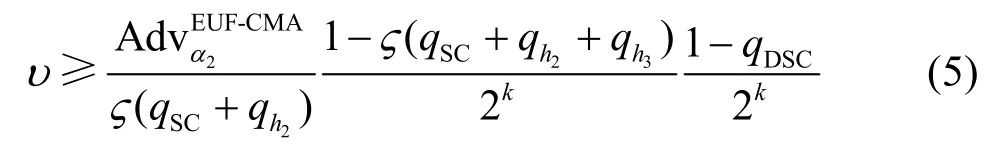
证明在游戏类型2 中，不同于游戏类型1，攻击者α2可以获得系统主密钥信息，但是不能对用户的公钥进行替换，对于定理4 的证明与定理3 的证明类似，易得定理4 成立。证毕。

5 效率分析

5.1 加密方案效率

本文的多接收方签密方案以及广义签密方案是在3.1 节中提出的多次加密McEliece 方案基础上进行构造的。由3.1 的加密方案可以看出，该方案采用的是 QC-LDPC 码，该码相比于Goppa 码等其他码字存储起来消耗更少的空间，且具有更高的传信率。另一方面，虽然该方案进行了多次加密，但是采用同一个码字产生的同一个公钥，解密也采用该码字产生的同一个私钥，因此多次加密的McEliece 方案能够保持与采用QC-LDPC 码的普通McEliece 方案同样的密钥存储量，且能够满足更高的安全需求。具体比较如表1 所示。

由表1 可以看出，采用Goppa 码的McEliece方案所选用的Goppa 码维度相比(QC-LDPC)-M 以及多次加密的McEliece 方案小许多，尽管如此，采用Goppa 码的McEliece 方案的公钥量为67 072 B，相比另外两者6 048 B 的公钥量还是大了许多，而且能够加密的明文量仅为524 bit，相比另外两者的12 096 bit 少了许多。通过公钥量一栏还可以看出，多次加密的McEliece 方案虽然采用多次加密的方法降低对译码错误的影响，从而具有了更高的安全性，但是与普通的采用QC-LPDC 码的McEliece 方案的密钥量相同，正如之前所述，这是由于多次加解密所采用的密钥是相同的，因此多次加密的McEliece 方案具有较好的性能。其中b代表多次加密的次数，即产生的密文数量。

5.2 多接收方的签密与广义签密方案效率

3.3 节与3.4节的签密和广义签密方案在参数生成以及系统密钥和用户密钥的生成上是相同的，因此从多接收方的广义签密分析方案的密钥量相等即可。取(16 128,12 096)维的QC-LDPC 码进行如表2 所示的比较。

由表2 对比分析可以看出，本文的多接收方广义签密方案不仅可以实现签密功能以及在签名、加密、签密方案三者之间的自适应转换，而且相比先签名后加密方案在私钥量上减少了31 752 KB，这些减少量的存在是由于CFS 签名方案与多次加密-M方案在置换矩阵P上的共用。先签名后加密方案与本文广义签密方案的密文量都是16 128(b+2)bit，相比直接将二者相加的密文量多了16 128 bit，这是因为还存在使用系统公钥加密产生的密文x，但这保证了系统用户以外的用户无法获知系统内部的信息。通过表2 可以看出，本文多接收方广义签密方案具有较好的使用前景。

表1 方案性能对比

表2 密钥量对比

将本文多接收方的广义签密方案与其他多接收方签密方案进行效率比较，如表3 所示。其中，ς代表多接收方用户数量。由表3 可以看出，本文的广义签密方案相比Li 等[32]方案、朱辉等[33]方案、Selvi 等[25]方案，没有复杂的指数运算以及双线性对运算，而本文方案多了矩阵运算。指数运算以及双线性对运算相比矩阵运算的效率较低，且消耗更多的资源，因此本文方案没有复杂的指数运算以及双线性对运算，这是提高效率的一大优势，由于是基于编码密码进行广义签密方案的构造，因此能够抵抗量子计算机攻击，这也是相比基于传统公钥密码构造签密方案的优势之一。

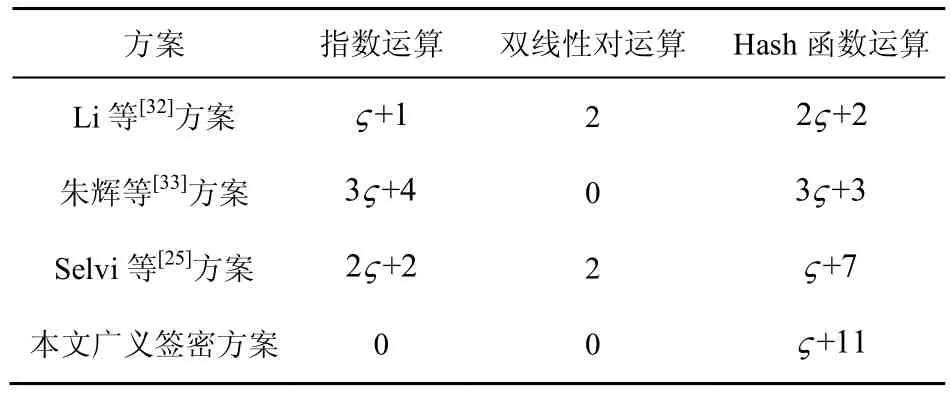
表3 签密方案效率对比

6 结束语

本文提出了能够满足IND-CCA2 安全的多次加密McEliece 方案，该加密方案采用QC-LDPC码进行构造且多次加密与解密所采用的都是同一对公私钥，因此能够在保证密钥储存量合适的前提下达到更高的安全级别。依托多次加密的McEliece 方案与CFS 签名方案，提出基于编码的多接收方的签密方案，进而在该签密方案的基础上进行改进提出了基于编码的多接收方的广义签密方案。新的广义签密方案在机密性方面满足IND-CCA 2 安全，在不可伪造性方面满足EUF-CMA 安全。本文广义签密方案在密钥量以及密文量方面具有一定优势，而且相比基于传统公钥密码的多接收方签密方案没有复杂的双线性对运算以及指数运算。最后将该多接收方的广义签密与多接收方通信模型相结合能够实现对不同安全级别用户的访问控制，能够满足系统的多种安全需求。