基于K-ELM和GMM的氮氧化物排放预测

陈 琪，续欣莹+，谢 珺，付文华

(1.太原理工大学 电气与动力工程学院，山西 太原 030024；2.太原理工大学 信息与计算机学院，山西 晋中 030600)

0 引 言

近些年来，随着统计学及神经网络的发展，支持向量机(support vector machine，SVM)和神经网络(artificial neural networks，ANN)被广泛应用于锅炉NOx排放建模预测[1-3]。余廷芳等[4]分别使用径向基(RBF)神经网络和BP神经网络(BPNN)对NOx进行建模；宋清昆等[5]利用SVM对锅炉NOx排放特性进行建模并采用改进的果蝇算法对模型参数进行优化；张文广等[6]使用最小二乘支持向量机(least squares support vector machine，LS-SVM)对锅炉NOx排放进行建模，采用果蝇算法对LS-SVM模型的超参数进行寻优。然而由于ANN容易陷于过拟合，SVM受限于二次规划，大部分采用它们研究建模的多是人为选择后的小样本。而这一方面会使得模型对于远离建模工况点的目标预测泛化能力降低，另一方面会使得模型本身因为人为剔除的因素丢失一些有用的信息。当这些算法采用大规模数据进行建模时，则往往会陷入过拟合或者耗费大量的时间。在大规模样本数据建模方面，国内外许多学者也进行了研究[7-9]。虽然周昊等[8]、徐晨晨等[9]一些学者很好地解决了电站锅炉大规模数据建模的问题，但是他们建模时选取的样本数据都是在确定采样时间后进行直接选取，并未考虑到电站实际运行中工况样本不均衡分布的特性。为了解决电站锅炉大规模数据建模问题，并考虑到锅炉工况样本分布的不均衡性，本文根据电站锅炉历史运行数据的负荷分布对其进行高斯混合聚类，然后根据GMM中各个分量的混合系数进行数据均衡化处理，采用K-ELM对处理后的数据建立NOx排放模型，实验结果验证了所提方法能够快速地建立NOx排放模型，有效地减少了建模时间，并且具有良好的泛化能力。

1 核极限学习机(K-ELM)

极限学习机[10](extreme learning machine，ELM)是黄广斌等提出的一种单隐层前馈神经网络(SLFNs)算法，该算法具有学习速度快、结构简单，同时人为干预少和泛化能力强等优点。被广泛应用于分类及回归等应用领域。黄广斌等[10]在支持向量机学习原理的基础上对极限学习机进行了改进，提出了核极限学习机(Kernel ELM, K-ELM)。K-ELM不仅具有ELM的诸多优点，而且由于其无需设置隐含层节点数，更利于模型的建立。

极限学习机的SLFNs模型可描述为

f(x)=h(x)β=Ηβ

(1)

式中：x为样本输入，f(x) 为神经网络的输出，h(x)、Η表示隐含层特征映射矩阵，β表示输出权重矩阵。

根据文献[10]，核极限学习机对应的模型为

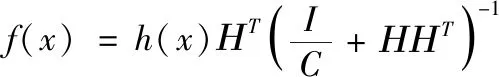
(2)

式中：C为正则化因子，T为样本对应的输出。K-ELM的核矩阵定义如下所示

ΩELM=ΗΗT：ΩELMi,j=h(xi)h(xj)=K(xi,xj)

(3)

本文中使用径向基函数(RBF)作为SLFNs模型的核函数，即

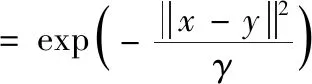
(4)

在使用K-ELM进行建模时，正则化因子C与核函数参数γ需要进行设定，参数的设定影响到K-ELM模型的性能。

2 高斯混合聚类

2.1 高斯混合模型(GMM)

高斯混合模型(Gaussian mixed model，GMM)是多个高斯分布函数的线性组合，理论上随着模型中高斯分布函数的增多，它可以精确地拟合任意复杂类型的分布，通常用于解决同一集合下的数据包含多个不同分布的情况。因此常常被用来解决聚类问题。

设有随机变量X，则混合高斯模型可以用下式表示

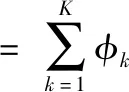
(5)

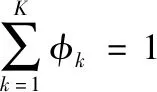
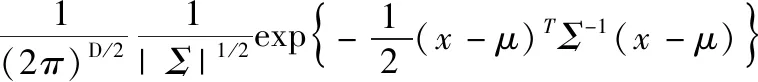
(6)

式中：D为数据维数，μ为其均值向量，Σ为其协方差矩阵。

2.2 EM算法求GMM聚类

期望最大化算法(expectation-maximum，EM)是一种迭代优化策略，经常被用来求解聚类问题。其每一次迭代都分为两步，其中一步为期望步(E步)，另一步为极大步(M步)。

记θ={φ1,…,φK,μ1,…,μK,Σ1,…,ΣK} 为高斯混合分布的参数集合。给定服从高斯混合分布的独立同分布样本集X={x1,x2,…,xm}。 令zi∈{1,2,…,K} 表示生成xi的高斯混合分量，其取值未知。显然zi的先验分布P(zi=k) 对应于φk(k=1,2,…,K)。 根据贝叶斯定理，zi的后验分布对应于

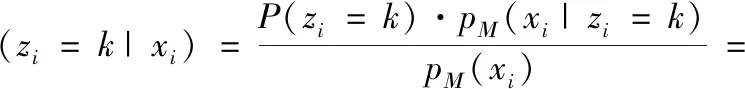
(7)

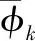
(8)

当高斯混合分布已知时，高斯混合聚类将样本集X划分为k个簇，C={C1,C2,…,Ck}，每个样本xi的簇标记λi根据如下公式进行确定

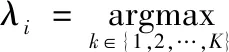
(9)

高斯混合模型的聚类求解可以根据EM算法被整合为以下两步：①根据zi对应的φk概率选择第k个高斯模型；②利用第k个模型生成其对应的样本Ck。

具体步骤如算法1所示：

Algorithm 1： EM for Gaussian Mixture Model

Input: 样本集X={x1,x2,…,xn}; 高斯混合分量个数K.

Process：

(2)repeat

(3)Estep: fori=1,…,nk=1,…,K

根据式(7)计算由各混合分量生成的后验概率，即γik=pΜ(zi=k|xi)

(4)Mstep: fork=1,…,K

新混合系数：φ′k=nk/n;

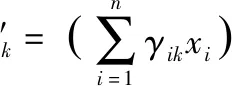
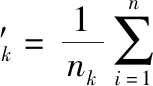
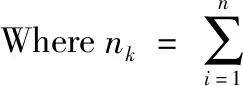
(6)untilconvergence.

(7)Ci=∅(1≤i≤K)

(8) fori=1,…,n

根据式(9)确定xi的簇标记λi；

将xi划分到相应的簇:Cλi=Cλi∪{xi}

Output: 簇划分C={C1,C2,…,Ck}.

3 锅炉介绍及数据准备

本文的研究基于某电厂600 MW机组的历史运行数据，该锅炉为亚临界压力、自然循环、前后墙对冲燃烧、单炉膛平衡通风、一次中间再热、固态排渣、尾部双烟道、紧身封闭、全钢架构的Π型汽包炉。

从该电厂的DCS系统中选取锅炉负荷跨度较大的一天的历史运行数据，采样周期为10 s，共8640组数据。由于各个测点的采样时间不统一并且有异常点的存在，剔除数据中的一部分异常点，并利用线性插值法对数据进行标准化处理。使得最终处理后的数据样本为各测点每10 s就采集一次的数据。根据锅炉燃烧机理选用锅炉负荷(1项)，一次风风速(6项)，二次风风速(14项)，二次风压 (2项)，二次风压偏差(1项)，二次风量(10项)，磨煤机给粉量(6项)，烟气含氧量(5项)，排烟温度(1项)，燃尽风挡板开度参数(8项)，共计54维参数作为模型的输入量(当天燃烧用煤为同种煤质，故不考虑煤质影响)。NOx排放值作为模型的输出量。模型输入量及输出量的取值范围见表1。

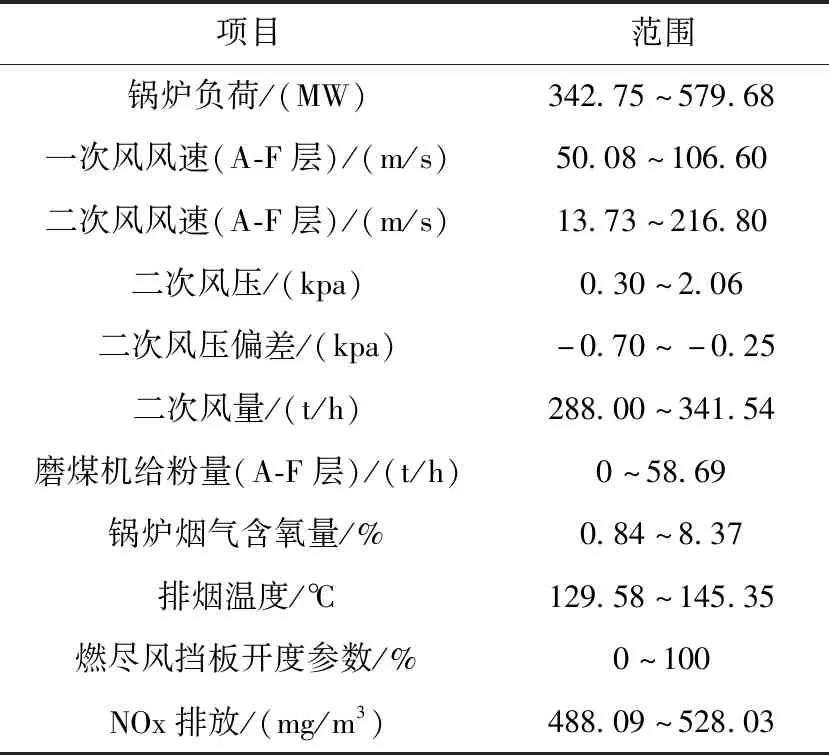
表1 实验样本数据分布

根据表1中的各参数取值范围将数据归一化到[-1,1]。归一化公式如下所示

(10)

式中：x*为归一化后的样本，x为原始样本，xmax、xmin分别为原始样本参数对应的最大值与最小值。

4 建模及讨论

第一部分我们使用K-ELM对锅炉数据进行建模，并采用交叉验证法和网格优化算法对模型参数进行寻优，这部分采用全部8640组工况数据进行建模分析，随机选取80%的工况数据作为训练样本，20%作为测试样本；第二部分，我们随机划分不同大小的样本数据，然后考察K-ELM、SVM、LS-SVM及BPNN算法在模型训练时间、预测精度等方面的性能，建模相应实验数据的训练样本和测试样本划分比例同第一部分。第三部分，我们根据锅炉实际运行状况使用GMM对锅炉原始样本数据进行聚类，并根据聚类结果对建模样本进行均衡化处理，建立GMM-K-ELM模型，然后与不同方式选取样本数据进行建模的K-ELM模型相比较。

4.1 K-ELM建模

为了验证模型的预测能力，本文采用均方根误差(root mean squared errors，RMSE)，平均相对误差(mean relative error，MRE)和决定系数R2来评价模型的预测能力，具体公式如下所示

(11)

(12)

(13)

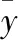
采用全部8640组工况数据进行K-ELM建模，随机选取其中80%的样本数据作为训练样本，剩余20%作为测试样本。K-ELM模型的学习能力和泛化能力取决于K-ELM的正则化因子C和核函数参数γ。使用网格优化算法对 K-ELM 中的正则化因子C与核函数参数γ进行寻优。为了防止训练模型过拟合，采用10阶交叉验证，首先将训练样本分成大致相等的10组，然后利用其中的9组数据训练模型，对剩下的1组样本进行测试，并循环进行10次，使得每组数据均进行过一次测试，把10次测试的总测试均方根误差的平均作为评价模型参数的指标。选定C、γ的变化范围为log2C=[-12,12]，log2γ=[-12,12]，区间步长为1，将总测试均方根误差的平均值RMSE归一化到[0,1]中，寻优结果如图1(a)所示。由于参数变化范围较大，我们根据图1(a)缩小C、γ的范围，确定log2C、log2γ的搜索范围分别为[6,12]、[-4,4]，区间步长为0.2，再次寻优结果如图1(b)所示。

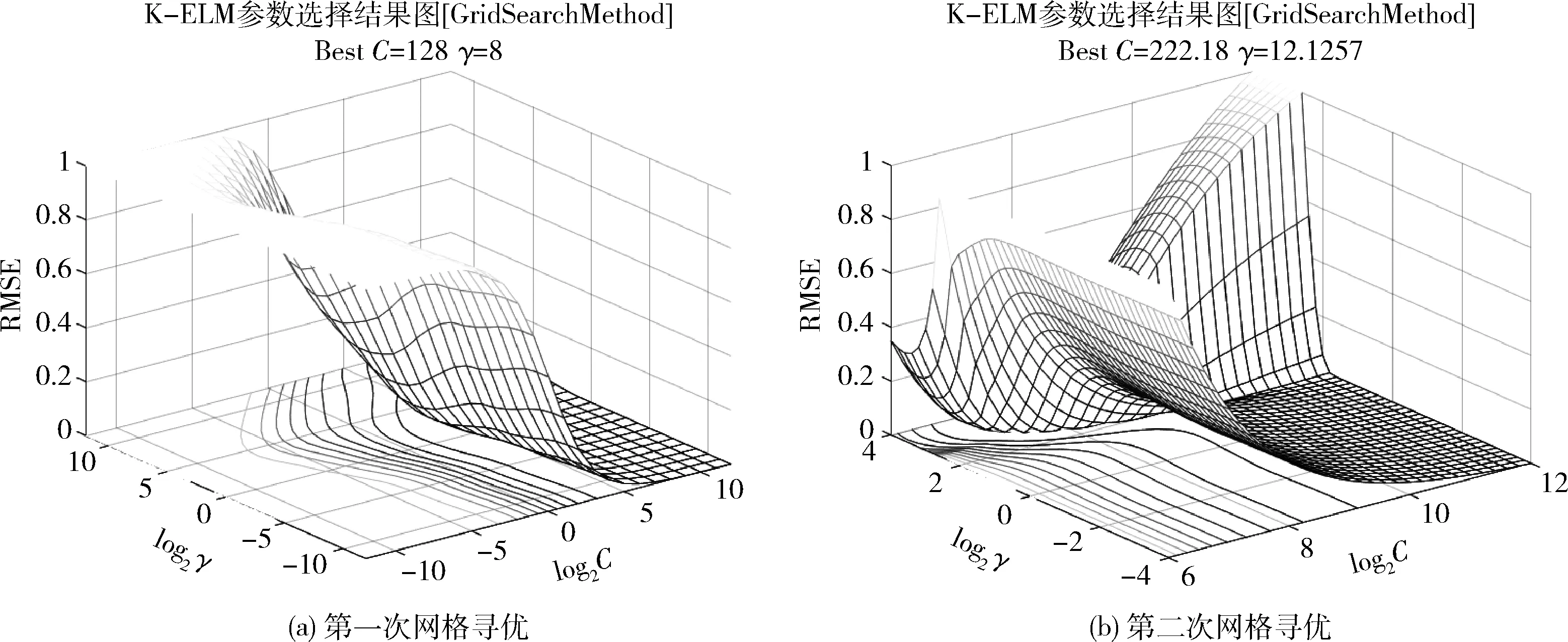
图1 K-ELM参数网格寻优结果

根据寻优结果，选定K-ELM模型中的参数组 (C,γ) 为(222.18,12.1257)。然后建立NOx排放的K-ELM模型，并对测试样本进行预测，预测结果如图2所示。可以看到K-ELM模型的预测值与测量值非常吻合。模型对测试样本的R2=0.9701，MRE=0.0291,RMSE=0.0619，模型的泛化性较好，可以准确地对NOx排放值进行预测。

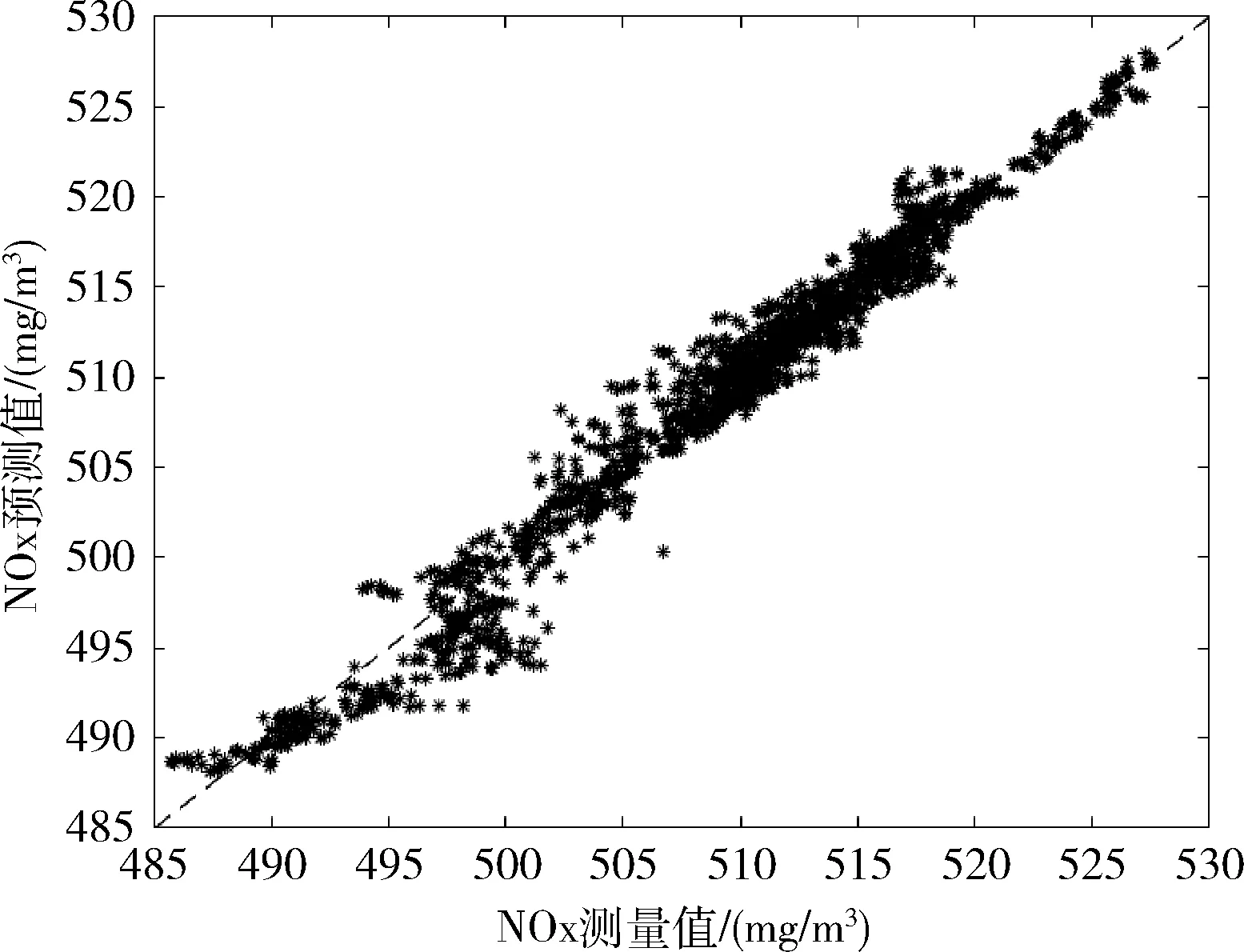
图2 预测值和测量值对比

4.2 多种算法对比

为了比较K-ELM和其它常用算法，本文同时采用了SVM、LS-SVM以及BPNN算法对实验数据进行建模。同时为了比较数据集大小变化的情况下各个算法之间的特性，首先在8640组数据中分别随机选取其10%，30%，50%，70%，100%的数据量作为新的数据集；对于不同大小的数据集，随机选取其80%作为训练样本，剩余20%作为测试样本。K-ELM、SVM、LS-SVM算法均采用相同的RBF函数，同样选用网格寻优法对其它两种算法的参数进行两次寻优，两次网格寻优过程中参数变化的步长均与K-ELM相同。所有算法的参数设置见表2。

表2 各算法参数设置

各个算法之间的对比指标包括：MRE、RMSE、R2以及建模时间Time，实验结果如图3所示。可以看到，在不同数据集下，K-ELM在MRE、RMSE、R2上皆优于其它3种算法，其预测精度最高，且其建模时间最短。同时随着实验数据的增加，4种算法的预测精度均有所提升，当数据量大于70%时，各个算法的MRE、RMSE减小缓慢，其决定系数R2提升也趋于平缓，但是由于数据量的增加，各个算法的建模时间显著增加。

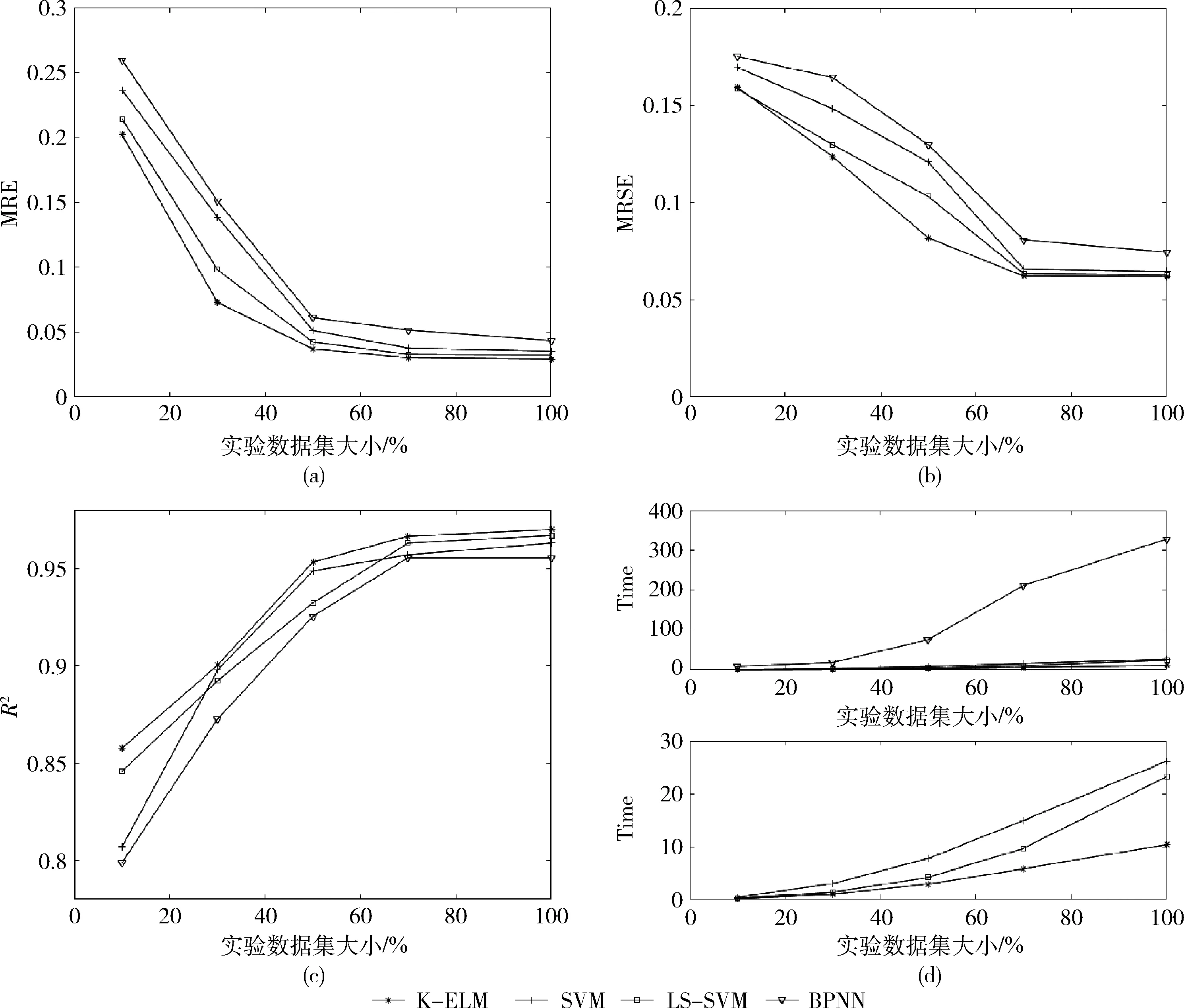
图3 各算法性能比较

4.3 GMM-K-ELM

为了适应电网用电需求，电厂需要不断调整各机组的发电量，如图4所示为该电厂2014年11月1日的某机组的锅炉负荷运行变化，可以看到锅炉负荷在早8点前、晚8点后以及中午的一个小时，基本在350 MW附近波动，其它时间的负荷变化基本反映了不同时间段电网的调电需求。可以看到各个负荷区间的样本数呈现出较大的不均衡性，如果将所有数据都用来建模，那么所得到的样本集可能会出现一个问题，某些负荷段的样本数据多，而另一些负荷段的数据样本少。某一负荷段的样本数据过多则会造成所含信息冗余，使得建模时间增大，计算复杂度提升。而简单的对数据进行随机选取或等间隔选取，并不能解决样本数据的不均衡性，且不利于对数据进行充分的使用。

图4 2014年11月1日锅炉负荷变化

本文提出了一种基于K-ELM和GMM的NOx排放建模方法，算法步骤如下所示：

步骤1 根据锅炉负荷取值范围(xmin,xmax)，以每区间10 MW为标准划分区间，将其等分为Km=round((xmax-xmin)/10) 个区间 (Km≥2)； 并将高斯混合模型设计为k个高斯混合分量 (k=Km)；

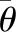
步骤3 根据算法1进行聚类，得到聚类结果C={C1,C2,…,Ck}，如果距离最近的高斯混合分量均值差的绝对值小于5，则k←k-1，并返回步骤(2)；

步骤4 根据聚类结果对锅炉样本数据进行均衡化处理。混合系数大于1/Km且方差小于10的聚类样本数据进行重新采样(随机采样)，采样公式如下所示

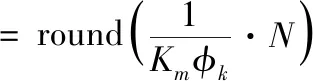
其中，round() 为四舍五入取整函数，N为聚类中所含样本个数，Km为初始聚类类别数(即初始区间划分数)，φk为聚类所对应的混合系数。

步骤5 使用均衡化处理过后的数据进行NOx排放的K-ELM建模。

根据以上方法对锅炉样本数据进行聚类，聚类结果见表3，可以看到只需要对序号为1、3、5的样本进行重新采样。重新采样后总的样本数据为2568组，约占总数据量的29.72%。

表3 锅炉样本数据聚类结果

使用经过GMM聚类重新采样后的数据进行K-ELM建模，为了说明GMM-K-ELM的性能优势，我们采用4组实验方案：方案一：GMM-K-ELM建模；方案二：随机选取30%的数据建立K-ELM模型；方案三：等间隔抽取全部数据的1/3建立K-ELM模型；方案四：使用全部8640组数据建立K-ELM模型。各组方案均进行50次实验，所有方案之间的对比指标包括：MRE、RMSE、R2，实验结果如图5所示。

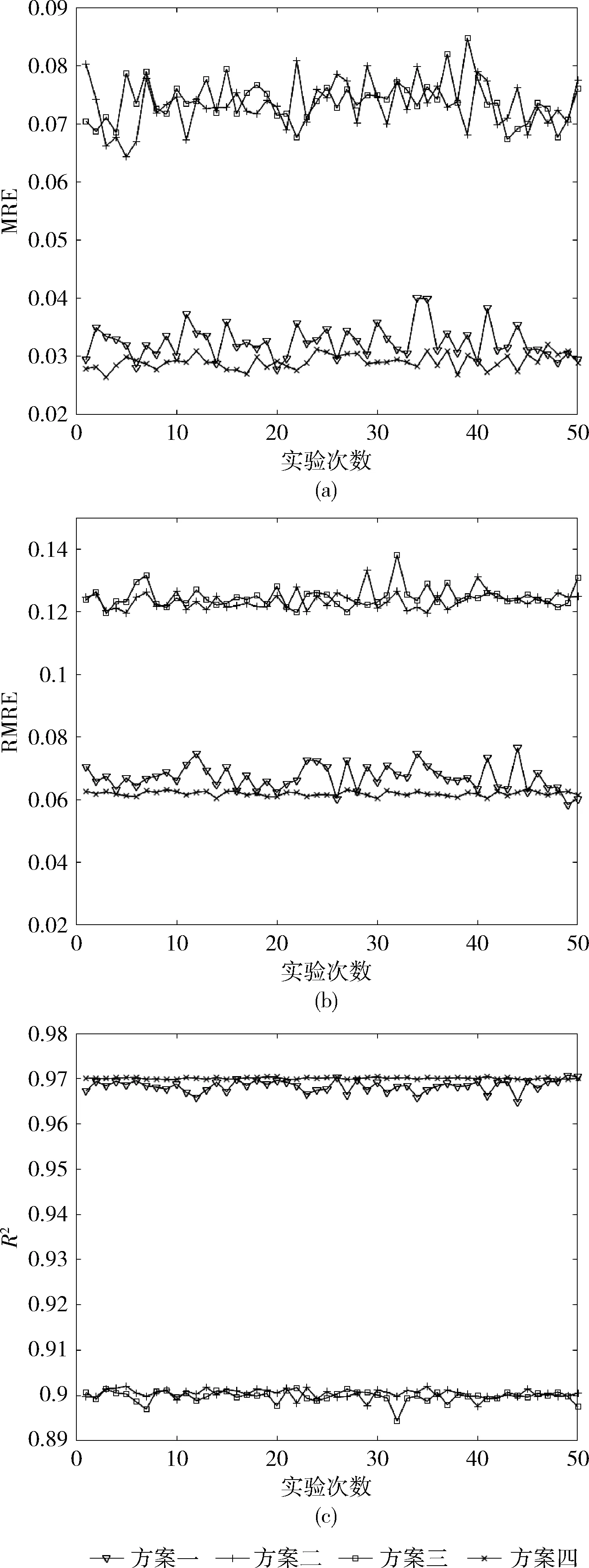
图5 各方案实验结果

从图5中可以看到方案一的MRE、MRSE、R2均优于方案二和方案三，说明其预测精度好于方案二和方案三；同时方案一的R2稳定在0.9653以上，MRE、RMSE与方案四非常接近，说明其预测精度较好，但是其数据量只占方案四的29.72%，其建模时间仅为方案四的7.95%。由此我们认为使用GMM-K-ELM进行大规模锅炉数据建模是可行的。与使用全部数据直接进行K-ELM建模相比，它们预测精度相近，但其模型训练时间更短，在模型数据规模成比例增加时，其优势更加明显。

5 结束语

本文比较了多种算法在大规模锅炉运行数据建模时的特性，结果表明K-ELM算法的预测精度高，建模时间短，总体优于其它算法。进一步地，基于电站锅炉运行的实际情况，提出一种基于K-ELM和GMM的氮氧化物排放建模方法，采用高斯混合聚类方法对建模数据进行均衡化处理，并使用K-ELM对其进行建模，在使用同等数据量进行建模时，进一步地提高了模型的泛化能力。多种对比实验结果显示，本文所提出的GMM-K-ELM建模方法，应用于真实的电站大规模锅炉运行数据建模中，能够快速地建立燃烧模型，有效地降低了计算复杂度，并且具有良好的泛化性能。