时空RPCA在复杂场景下的运动目标检测
2020-02-08张超婕
张超婕,余 勤
(四川大学 电气信息学院,四川 成都 610065)
0 引 言
在计算机视觉应用中,数据的维度通常非常高。主成分分析(PCA)[1]是一种有效降低维数的方法。然而,PCA对于异常点和稀疏大噪声的数据非常敏感。为解决此问题,Candes等[2]提出鲁棒主成分分析(RPCA),该模型将观测数据利用原始数据矩阵的低秩性和误差矩阵的稀疏性分为低秩背景部分和稀疏前景部分。RPCA模型广泛应用于图像去噪、视频处理和生物信息等领域[3-5]。但RPCA模型中核范数并不是秩函数的最佳近似。为更准确刻画低秩背景部分,He等[6]根据矩阵的非凸加权核范数能更准确地逼近矩阵的秩函数,提出了WMPCA模型。然而该模型并未考虑到时间和空间上的连续性,使得复杂背景下运动目标的检测效果不理想。Zhou等[7]注意到运动目标具有区域连续性,因此在RPCA模型的基础上加入该先验知识提出了DECOLOR模型,虽然分割性能得到提高,但该模型严格的平滑约束使得运动目标检测不完整。为了保留高维空间的局部几何结构,研究者们提出了图的降维方法。Yan等[8]提出了图嵌入框架模型,可将一些经典的降维算法如PCA、LDA和LPP等嵌入到该框架中。据此Jiang等[9]提出了图拉普拉斯PCA(GLRPCA),但该模型对数据损坏或异常点非常敏感。
本文提出一种基于非凸加权核范数的时空低秩RPCA算法。首先将RPCA模型中核范数替换为非凸加权核范数对低秩背景矩阵进行约束。其次构造观测矩阵的时空图,通过计算时空图拉普拉斯算子以得到局部相似性。在改进RPCA算法的基础上融入时空图拉普拉斯正则项以提高模型对噪声和动态背景的鲁棒性。最后用自适应惩罚项线性化交替方向法[10](LADMAP)求解出本文提出的模型。
1 鲁棒主成分分析及相关研究
1.1 预备知识

定义2[12]加权奇异收缩算子T。在矩阵D∈Rm×n中,D可以通过奇异值分解为D=UΣV,Σ=Diag({σi(D),1≤i≤n})。 对于任意的v>0,加权奇异值收缩算子T(D,W) 可以表示为
T(D,W)=Udiag(σi(D)-λωi)+VT
(1)
其中,ωi(i=1,2,…,n) 是g(·)的次梯度,σi(i=1,2,…,n) 是D的第i个奇异值。对于任意a∈R,(t-a)+=max(t-a,0)。
引理1 非凸加权核范数求解。对于任意v>0,W=diag(w),给定矩阵X,Y∈Rm×n(n (2) Sτ(X)=sgn(Y)·max(|Y|-τ,0) (3) 为克服主成分分析(PCA)在前景检测应用中的缺陷,根据稀疏矩阵对大噪声和异常点具有鲁棒性的特点,提出鲁棒主成分分析模型(RPCA)。将n帧图像组成的观测矩阵表示为D=[d1,d2,…dn]∈Rm×n,其中di表示第i帧图像矢量化的列向量,每帧图像有m个像素点。鲁棒主成分分析模型(RPCA)认为可将观测矩阵D分解成低秩背景矩阵B∈Rm×n和稀疏前景矩阵F∈Rm×n。 其模型如下所示 (4) 但由于上式的求解是一个非确定性多项式难题(NP-Hard),故引入凸优化方法:核范数是矩阵秩的包络,而矩阵中l1范数是l0范数的凸包,故可以将式(4)松弛优化为式(5),如下所示 (5) 通过最小化上式可以有效分离出视频的前景和背景。虽然RPCA模型对异常点具有鲁棒性,但是由于该模型采用l1范数去表征运动目标的稀疏矩阵,并没有考虑到运动目标的时空连续性,因此在复杂背景下运动目标的检测效果不佳。 传统的矩阵分解模型很难将运动目标从复杂背景中分离出来。而拉普拉斯特征映射(LE)[14]在一定程度上保留了局部信息,并在低维空间中最大化数据集内部流形的平滑性,使得对误差噪声或离群值不太敏感,具有很好的稳定性。对于数据集Y={y1,y2,…yn},其目标函数定义如下 (6) 其中,Wij表示近邻点之间的权值,用于度量yi与yj之间的相似性。其中Wij有k近邻和ε近邻两种形式 (7) 或 (8) 其中,ε中为大于0的常数,N(xi)表示数据集中距离xi最近的k个邻居的集合。σ为热核参数,通过热核函数可知,当两个点间距越小时,Wij值越大,即映射到低维空间时两个点越接近。化简式(6)可得 (9) 根据上部分理论的铺垫,本文得到以下模型 (10) 由于传统的RPCA模型缺乏结构信息,因此对于复杂背景场景运动目标检测效果较差。通过对低秩背景矩阵B实施时空约束以更有效处理该问题。 构造GT=(D,WT) 为时间图,其中顶点d为观测矩阵D的某一帧图像,WT表示邻接矩阵。该图采用k近邻法构造。首先根据欧几里德距离搜索所有列的最近的k个邻居,其中每个节点都与最近的邻居连接。对于时间图GT,WT是包含所有成对相似性的wij矩阵 (11) 其中,σ为热核因子,将其计算为节点之间的平均距离。其正则化约束由下式给出 (12) 得到归一化时间图拉普拉斯矩阵ΦT ΦT(i,j)ij=A-1/2(A-W)A-1/2=I-A-1/2WA-1/2 (13) GS=(D′,WS) 为空间图,其中顶点为观测矩阵D的某一行,WS表示行矩阵间邻接矩阵。空间图GS编码了空间位置之间的相似性。对于空间图的拉普拉斯算子的构造,选择在观测矩阵D的补丁级上实施平滑,对于矩阵D第一帧中的每个像素,采用一个大小为u2的补丁。同理得到空间拉普拉斯矩阵ΦS。 模型(10)本质上为凸优化问题,故采用增广拉格朗日乘子法ALM求解,构造的增广拉格朗日函数如下式 (14) 其中,X,Y,Z∈Rm×n为拉格朗日乘子,μ>0为惩罚因子,<·>为矩阵内积。该模型采用自适应惩罚项线性化交替方向法(LADMAP)进行求解,具体求解方法为:每次迭代只更新一个变量且固定其它所有变量。相对于传统的交替方向法而言,该算法只需要引入辅助变量,在减少计算量的同时提高了计算精度。其求解过程如下。 固定F、L、H、X、Y、Z、μ,更新背景矩阵B (15) 算法1:低秩背景矩阵估计 输入:μ,观测矩阵D∈Rm×n,稀疏前景矩阵F∈Rm×n 输出:Bk+1 初始化:k=0,Bk=0 迭代: (1)根据引理1更新Bk+1 (16) 固定B、L、H、X、Y、Z、μ,更新目标矩阵F (17) 根据引理2,可得到F的封闭解为 (18) 固定B、F、H、X、Y、Z、μ,更新时间低秩矩阵L (19) 由上式为光滑函数,采用投影共轭梯度法求出L封闭解为 (20) 固定B、F、L、X、Y、Z、μ,更新空间低秩矩阵H (21) 同理用投影共轭梯度法求出L封闭解为 (22) 固定B、F、L、H、μ,更新拉格朗日乘子X、Y、Z Xk+1=Xk+μk(D-Bk+1-Fk+1) (23) Yk+1=Yk+μk(Bk+1-Lk+1) (24) Zk+1=Zk+μk(Bk+1-Hk+1) (25) 固定B、F、L、H、X、Y、Z,更新惩罚因子μ μk+1=min(ρμk,μmax) (26) 其中,ρ为常数。根据KKT条件,其收敛条件如下 (27) 算法2:式(10)模型求解算法 输入:D∈Rm×n,λ,γ1,γ2,ΦS,ΦT 输出:B,F 初始化:k=0,B0=F0=L0=H0=0,X0=Y0=Z0=0, μ0=0.1,μmax=1010,ρ=1.1,ε=10-4,ρ=1.1 迭代: (5)Xk+1=Xk+μk(D-Bk+1-Fk+1)参见式(23); (6)Yk+1=Yk+μk(Bk+1-Lk+1) 参见式(24); (7)Zk+1=Zk+μk(Bk+1-Hk+1) 参见式(25); (8)μk+1=min(ρμk,μmax) 参见式(26); (9)根据式(27)检查是否收敛。 为了进行验证,我们从数据库change detection video database[15]中选取了5组具有挑战性的数据集:①boats、②water surface、③fountain、④fall、⑤overpass对本文所提出的算法进行评估。实验的运行环境为Intel Core i5处理器,8 GB内存,win10操作系统;实验的软件环境为Matlab R2015a。将本文提出的算法与RPCA、WMPCA和DECOLOR模型进行比较,得到的结果如图1所示。本数据集分为3类:目标在复杂动态背景内缓慢运动:①boats、②water surface。背景包含可被检测运动前景的高动态区域:③fountain、④fall。运动目标在复杂场景中运动:⑤overpass。对比RPCA模型、WMPCA模型、DECOLOR模型和本文提出的模型在3种不同场景下的目标检测结果。其中RPCA模型和WMPCA模型对复杂背景的运动目标检测不适用,容易将运动背景误检成目标前景,但WMPCA模型相对于RPCA模型能取得更好的效果,其主要的原因在于WMPCA模型采用非凸加权核函数逼近秩函数,能够更好体现视频中低秩背景帧之间的强相关性;而DECO-LOR模型对比WMPCA模型和RPCA模型虽然融合了运动目标区域连续性提高了检测精度,但由于该模型过度的平滑约束导致检测到的运动目标不完整或误检现象;而本文融合了WMPCA的优点,同时在低秩背景矩阵上进行时空约束以保持局部信息,最终得到完整的运动目标。 图1 视频前景提取实验对比 本文采用峰值信噪比(peak signal to noise ratio,PSNR)对3种模型的背景恢复效果进行衡量,公式如下 (28) (29) (30) (31) (32) 其中,r为召回率(recall),p为准确率(precision, p)。TP(true positives)为检测中被正确分类的前景像素点数,FP(false positives)为检测中背景像素被错误分为前景的像素点数,FN(false negatives)为检测中前景被错误分为背景的像素点数。当综合性能指标越高,表示该模型的运动目标提取效果越好。 从表1可以看出动态背景的视频中,本文模型较RPCA、WMPCA与DECOLOR这3种模型在综合性能指标上有明显的提高。本文模型在低秩背景上进行时空约束从而降低了错分率,使得复杂背景下的运动目标检测准确率提高。从表2可以看出本文提出的方法信噪比PSNR比其它模型高得多。主要在于本文利用图拉普拉斯正则化的相似性思想从而保留了低秩背景的内在结构。即使被前景目标遮挡,也能够生成较为精确的背景模型。 表1 各模型召回率、准确率及综合性能指标F比较 表2 各算法峰值信噪比PSNR比较 在本文所提出的算法中,我们设置参数λ=1/max(m,n)。 对于参数γ1,γ2,通过实验发现,若测试场景为静态背景,则空间模型优于时间模型,此时应设置γ1<γ2; 若测试场景为动态场景或光线较暗,例如图1中的图(d),则时间模型优于空间模型,此时应设置γ1>γ2; 据此综合设置参数γ1=γ2=0.08。 本文提出了一种基于非凸加权核范数的时空低秩RPCA模型用于对复杂场景的运动目标检测,该模型在动态背景、光照渐变等复杂场景中能较准确地检测出运动目标。首先,利用加权核范数替代核范数用于视频的背景建模,同时对背景矩阵进行时空约束以保留局部信息,从而提高运动目标的检测精度。本文分别在5种不同的复杂场景下进行实验,与其它模型相比,本文所提出的模型对目标检测的效果最佳,且适用性最强。
1.2 鲁棒主成分分析(RPCA)


1.3 拉普拉斯特征映射


2 模型的建立及其求解


2.1 时空低秩正则化
2.2 改进RPCA算法




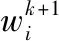










3 实验结果与分析
3.1 直观实验结果对比

3.2 实验结果分析

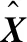


4 结束语
