基于准范数与零范数的矩阵恢复

张令威，刘光宇，吴哲夫，刘光灿

(南京信息工程大学 江苏省大数据分析技术重点实验室，江苏 南京 210044)

0 引 言

由于数据在采集、存储、传输的过程中很容易受到噪声的干扰，这为人们利用这些数据带去了更大的挑战。矩阵恢复的目的就是在矩阵的部分数据受到干扰的情况下恢复出原始的矩阵。

高维矩阵往往具有较高的相关性和冗余性[1]，因此矩阵一般具有低秩的结构，这种低秩性可以通过秩函数来衡量。而矩阵中存在的噪声通常具有稀疏性。因此可以将高维数据分解为一个低秩矩阵与一个稀疏矩阵之和[2]。然而，矩阵的秩函数是非凸且不连续的[3]，秩最小化问题也是NP难的，这使得直接求解秩函数十分困难。为了求解秩最小化问题，目前普遍的做法是使用秩函数最优的凸近似-核范数[4]来代替秩函数，理论证明，当问题符合某些特定的条件时，核范数最小化与秩函数最小化的求解结果是等价的。核范数的应用使得秩最小化问题转化成了凸问题，极大降低了求解的难度。

近年来矩阵恢复算法主获得了快速的发展，常用的有下述一些方法。鲁棒主成分分析(robust PCA，RPCA)[5]将矩阵分解为低秩矩阵与系数噪声矩阵，低秩表示(low-rank representation，LRR)[6,7]在RPCA的基础上做了延伸，认为数据集中的样本可以表示为一个字典中的基的线性组合，组合的系数应该是低秩的，LRR更好地捕捉了数据的真实分布情况。非凸近似函数Schatten-p范数[8,9]使用准范数作为秩函数的代替，获得了比核范数更精确的秩最小化结果。最近，基于Schatten-p范数的低秩矩阵分解[10]将待求解的矩阵分解为两个子矩阵的乘积，加速了准范数的求解过程。

本文使用准范数的低秩矩阵分解形式代替经典的核范数约束，使用零范数约束矩阵中的稀疏噪声部分，提出基于交替近似的线性最小化方法求解目标函数的优化问题。实验结果表明，本文的方法可以获得更加精确的低秩矩阵恢复结果，能够有效地去除矩阵中的噪声，同时也可以提高基于低秩表示的图像分类方法的效果。

1 低秩矩阵恢复简介

高维矩阵通常具有较高的相关性，而矩阵的秩相对于矩阵的行数或列数来说一般较小。低秩矩阵恢复就是将给定高维矩阵D(D∈m×n) 分解为一个低秩矩阵L(L∈m×n) 与一个稀疏噪声矩阵S(S∈m×n)，优化问题如下所示

(1)

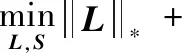
(2)

(3)

由于Schatten-p准范数的非凸性质，且求解问题是NP难的，因此基于直接求解准范数的方法通常无法进行大规模的应用。

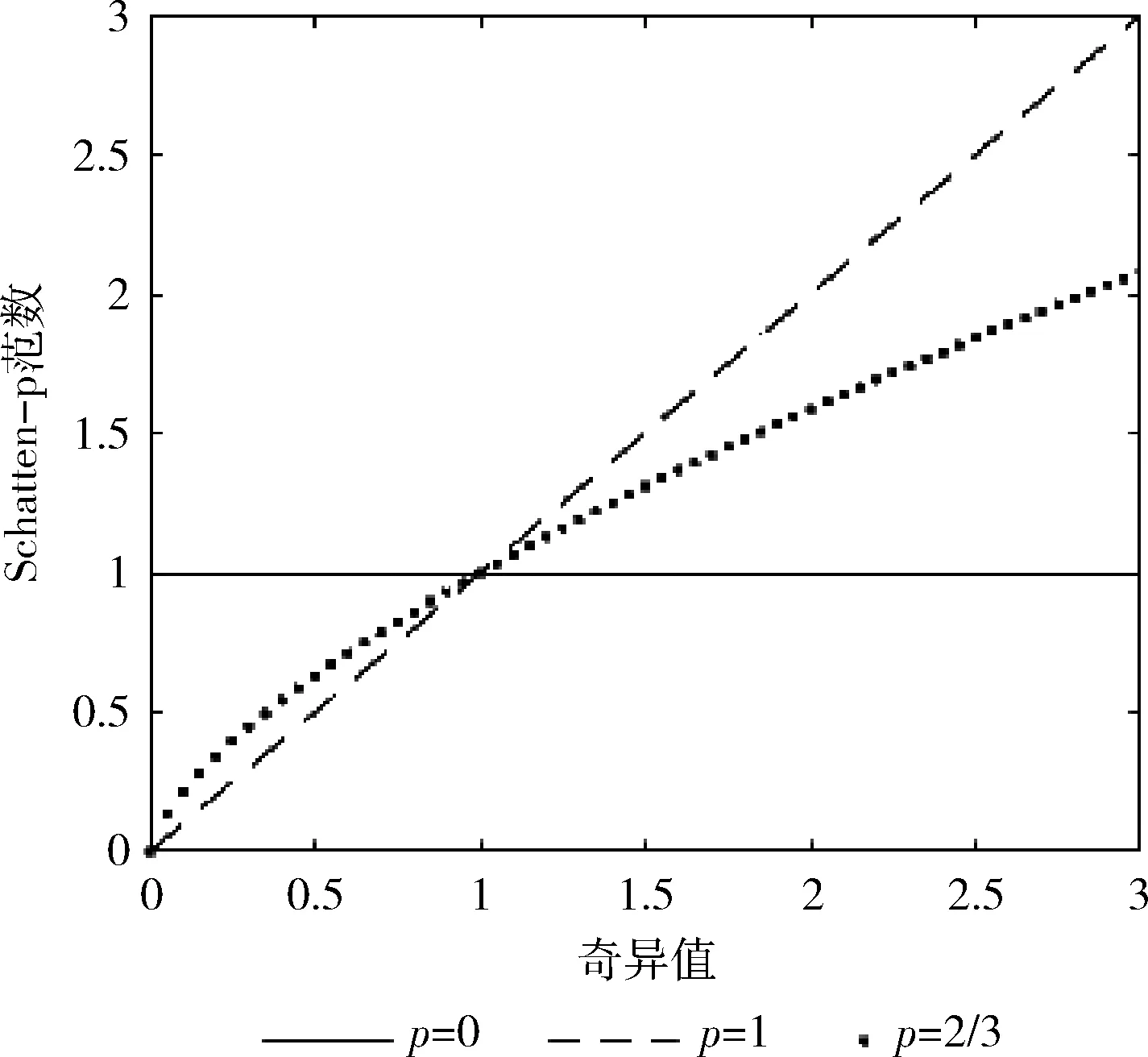
图1 Schatten-p范数曲线

2 基于准范数与零范数的矩阵恢复

2.1 目标函数的提出

(4)

2.2 基于交替近似的目标函数优化

由于矩阵Schatten-2/3准范数的非凸性质导致了求解的困难，Shang等[11]证明

(5)

其中，矩阵准范数被分解为两个因子矩阵，分别求解因子矩阵的F范数与核范数即可得到准范数的优化结果。利用这种性质，本文的目标函数变为如下形式

(6)

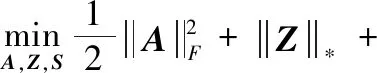
(7)

其中，参数α用来平衡扰动的大小。

零范数的求解是NP难的，本文提出了交替近似最小化的方法求解含有零范数的目标函数，式(7)可以分解为3个子问题交替进行迭代优化。

2.2.1 变量Z的更新

首先固定变量A，S，更新Z

(8)

式(8)没有闭式解，需要进行线性化得到具有闭式解的近似形式，研究证明

(9)

gl∶=AT(AXl-Bl)

(10)

由式(9)、式(10)两式可将式(8)转化为如下形式

(11)

对于形如式(11)的函数，首先引入收缩算子(shrinkage operator)[12]，定义为

(12)

根据奇异值阈值(singular value thresholding)[13]可得式(11)的闭式解为

(13)

2.2.2 变量A的更新

然后固定变量Z，S，更新A

(14)

上式对A求偏导可直接得到A的更新公式

Al+1=α(D-Sl)(Zl)T(I+αZl+1(Zl+1)T)-1

(15)

2.2.3 变量S的更新

最后固定变量A，Z，更新S

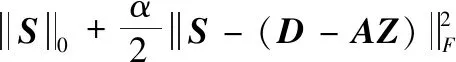
(16)

形如式(16)的函数可以使用硬阈值函数(Hard thresholding)[14]进行求解，首先引入硬阈值算子

(17)

则式(16)可用下式求解

(18)

求解本文目标函数的详细过程如下：输入原始矩阵D，参数λ,α；初始化A=I，使用RPCA方法的结果初始化Z和S，ρ=1.1； 根据式(13)、式(15)、式(18)更新变量Z,A,S直到满足收敛条件；输出两个因子矩阵Z，A，噪声矩阵S。 本文的收敛准则为|fk(A,Z,S)-fk+1(A,Z,S)|<10-6fk(A,Z,S)，其中fk(A,Z,S)为目标函数在第k步迭代时的函数值。

3 实验结果与分析

本文提出的方法在人工生成数据集与真实数据集上与RPCA算法[5]、字典搜索[1](dictionary pursuit，DP)算法进行了矩阵恢复的对比实验，还在LRR算法的基础上探索了本文的方法对于人脸识别任务的影响。本文实验环境为Intel酷睿i7-6700CPU，16G内存的戴尔台式电脑，使用MATLAB R2017a平台编程实现算法。

3.1 随机生成矩阵

图2 随机生成矩阵的恢复结果对比

3.2 文本去除

本文将提出的方法进行了文本去除实验的对比。真实图像的维度为256×256，秩为10。图3(a)展示了输入图像与原始图像。本实验中，文本部分可以看作矩阵恢复问题中的噪声部分。本文算法与RPCA，Dictionary Pursuit[1]进行了对比。

图3 文本去除结果对比

3.3 Essex人脸数据集

Essex人脸数据集由埃塞克斯大学所收集，被分为4个

表1 文本去除评价指标对比

目录:face94，face95，face96，grimace，共计395个人的人脸，每人20张图像，包含各种不同的种族血统的人。人群主要是一年级的本科学生，所以大多数图像的年龄在18-20岁之间，但是也含有部分老年人的图像。其中部分人脸图像带有眼镜或者胡须，face96中还包含了极端的表情变化。

本文将原始数据图像统一下采样至40×40像素，将每张人脸图像矢量化为1600维作为一个数据样本。实验中随机选取10，30，50个类别，每类随机选取6张图像加入不同大小的白块作为遮挡，以LRR算法为分类算法，通过搜索选取各算法的最优参数，以正确率为评价标准进行了对比实验。图4展示了所选数据集及加入遮挡后的部分图片样本。

图4 Essex人脸数据集

表2～表4展示了本文方法与RPCA、LRR方法进行人脸识别任务的结果。表2表明，当待分类的人脸图片较少时，本文方法能够显著提高分类结果的正确率。随着待分类图片逐渐增加，本文方法对分类结果的提升效果逐渐降低，但仍然获得了最好的结果。

表2 10类人脸识别正确率

表3 30类人脸识别正确率

表4 50类人脸识别正确率

3.4 参数选择

图5 参数α对算法影响

4 结束语

使用矩阵Schatten-2/3准范数代替常规的核范数作为秩函数的近似，并将准范数的求解分解为求解其两个因子矩阵的核范数与F范数，简化了准范数的优化难度，使用零范数代替l1范数作为稀疏噪声矩阵的约束，并提出了交替近似算法进行求解，最终获得了比l1范数更加精确的矩阵恢复效果。在人工生成矩阵、文本去除任务、Essex人脸数据集识别任务上同流行的矩阵恢复算法进行对比实验，验证了本文方法可以更有效地恢复被噪声干扰的矩阵，同时可以有效提高无监督人脸识别算法的准确性。