基于多种几何约束的图像误匹配剔除算法
2020-02-08刘李漫谭龙雨刘佳
刘李漫,谭龙雨,刘佳
(中南民族大学 生物医学工程学院,武汉 430074)
如何确定两幅有重叠场景的图像的像素之间的匹配对应关系是计算机视觉中的一个重要问题[1],在立体视觉、动作捕捉分析、三维重建等方面都具有广泛的应用[2],是解决这些问题的基础的一步.如果缺乏稳定的匹配对应点,那么以上问题就难以解决,或者是得不到令人满意的效果.
SIFT算法[3]是目前最常用的匹配方法,是图像匹配技术领域的一个里程碑[4,5].但是SIFT算法仅仅利用图像中的相邻局部信息进行匹配,而且需要遍历整个图像.因此对于图像中具有相似局部结构但位置并不对应的特征点极易发生错误匹配[6-8].再加上有些匹配的图像可能来源于不同的传感器或拍摄条件,因此图像之间匹配可能会受到尺度、光照、视角、方位等复杂变化因素的影响.同时仿射变换等[9]复杂因素也会使图像之间产生错误的匹配[10].
为了消除错误匹配对精度的影响,通常采用误匹配剔除算法对匹配结果进行优化.LMEDS[11]是鲁棒统计方法,该方法可以处理大量的错误匹配点,但是其缺点是计算效率低.M-estimation也是一种鲁棒性方法[12],它将对称且正定函数的残余项之和最小化,但是该方法需要事先给出模型参数较好的初始估计.RANSAC[13]是常用的随机抽样模型参数估计算法,其基本假设是样本中包含正确数据的内点和错误的外点,通过不断的迭代计算出能够适应绝大多数内点的基础矩阵模型,剔除不满足基础矩阵的模型外点[14].LI X R等提出对应函数的概念,给出一种剔除错误匹配点的方法ICF[15].该方法通过检测匹配点与估计函数对是否一致来剔除错误匹配点,可以处理存在未知的刚性或非刚性变换的图像匹配,且处理高错误率的匹配点时有很好的性能.WANG Y T等人基于拓扑聚类的应用,提出一种剔除宽基线的错误匹配算法[16].该方法对宽基线外点的剔除很有效,特别是对低精度的初始SIFT匹配.但是该方法比较敏感,对阀值的限定要求较高.ZHAO J等人基于矢量场学习,提出一种剔除错误匹配点的鲁棒性方法VFC[17].该方法是首次将矢量场应用于剔除误点在区分外点和内点的同时,计算出符合内点的矢量场.然而,该方法涉及到矩阵的谱分解,当匹配点数量很多的时候,计算效率不高.OLSSON C和ERIKSSON A提出使用对偶性剔除错误匹配点的方法[18].该方法应用于在已知旋转的变化剔除错误匹配点和大规模3D重建中.胡松等人通过自适应特征点邻域半径得到的邻域特征点数量及位置信息进行逐步求精,克服原算法不能处理尺度变换的情形,提出基于图像特征点信息的误匹配点剔除改进算法[19].该算法简单高效,具有尺度、旋转不变性,剔除误匹配点对能力较强.
1 基于多种几何约束的误匹配剔除算法
本节研究用于识别和剔除错误匹配的四种几何约束,以及每种约束对应的剔除算法.其基本思想是两幅图像的正确匹配点对之间应该具有几何关系的一致性,不满足这个一致性的匹配有可能是错误的匹配.本文设计了四种利用图形的几何约束剔除图像误匹配的具体方法,并通过将这四种子方法进行组合,设计提出了一个轻量级的、有效的误匹配剔除算法.
1.1 方向角算法
将两幅匹配图像I1和I2并列在一起,如图 1所示,其中I1和I2的边缘邻接.对于匹配图像中的任意匹配点对(d1,d2),其中d1位于图片I1中,d2位于图片I2中,连接点d1、d2做直线L,设直线L与X轴的夹角为匹配点对(d1,d2)的方向角θ(-90°<θ<90°),则对于匹配图像中的每一对匹配点对,都会对应于一个方向角θ.

图1 方向角示意图Fig.1 Direction angle diagram
(fp,tp)为一对匹配点对,fp在图像I1上,tp在图像I2上,其方向角为θp.检验该匹配点对是否为正确匹配,令fp为待判定点,tp为判定匹配点.假设fp周围邻域有点a1、b1、c1…k1共k个点,而这k个点在初始匹配中对应于I2上的匹配点为a2、b2、c2…k2,那么就有k个匹配对(a1,a2)、(b1,b2)、(c1,c2)…(k1,k2).这些匹配点对会分别产生方向角,记为θ1、θ2、θ3…θk.如果匹配对(fp,tp)是正确的匹配,那么它们产生的方向角θp在理论上其值会与θ1、θ2、θ3…θk的均值十分接近.反之,如果方向角θp与均值相差较大,超过阈值(实验中阈值取15效果最佳),那么就认为这个匹配对为错误的匹配.该算法的详细描述见算法1.

算法1:方向角算法输入:两幅图像I1和I2的初始SIFT匹配输出:保留的正确匹配1:取一对匹配点,获得该匹配在两幅图像I1和I2中的关键点序号(fp,tp),并令fp为待判定点,tp为判定匹配点2:根据SIFT中提取出来的位置信息计算I1中所有匹配点到当前待判定点fp之间的欧氏距离,将欧式距离按升序排序3:取出离判定点最近的至多30个匹配点在图像I1中所对应的序号.取这些相应匹配点对的方向角平均值4:将平均方向角与(fp,tp)点对的方向角做差,取绝对值,获得判定角差5:将判定差与阈值t(t=15)作比较,若小于t,则认为该匹配点对为正确匹配,否则认为其为错误匹配.由此即可判定该匹配点对是否正确6:若还有其他匹配,则取下一匹配判定
1.2 邻域信息算法
对图像I1上的待判定点fp与图像I2上的对应匹配点tp,假设fp周围邻域有点a1、b1、c1…k1共k个点,而这k个点在初始匹配中对应于I2上的匹配点为a2、b2、c2…k2,令I1上的k个点的点集为S1,I2上的k个点的点集为S2.检验点集S1与对应点集S2的中的匹配对个数,假设点集S1中有m个点与S2中的k个点存在匹配关系,则记待判定点fp的邻域对应百分比为m/k.显然,如果点对(fp,tp)为正确的匹配点对,那么fp邻域的点与tp邻域的点中必定存在一定数量的匹配点对,则m与k的值应该近似,其邻域对应百分比m/k应该大于某个阈值th(实验中th=50%时效果最佳).如果(fp,tp)为错误的匹配点对,那么点fp邻域与点tp邻域很难存在对应的关系,其邻域对应百分比m/k的值理论上接近0.根据此理论分析进行算法设计,可以判断点对(fp,tp)是否为正确的匹配点对.该算法的详细描述见算法2.

算法2:邻域信息算法输入:两幅图像I1和I2的初始SIFT匹配输出:保留的正确匹配1:取一对匹配点,获得该匹配在两幅图像I1和I2中的关键点序号(fp,tp)并令fp为待判定点,tp为判定匹配点2:根据SIFT中提取出来的位置信息计算I1中所有匹配点到当前待判定点fp之间的欧氏距离,将欧式距离按升序排序3:取出离判定点最近的至多30个匹配点在图像I1中所对应的序号4:取一个邻域中的关键点,找到其在I2中对应的匹配点5:对该邻域关键点的匹配点做类似待判定点的处理,获得它的邻域关键点集6:在这个邻域关键点集内查找判定匹配点.如果该邻域关键点集包含判定匹配点,则认为判定点对的正确可能性增大7:将所有邻域关键点都做完该处理后,统计成功匹配的邻域关键点对数量.将成功匹配的邻域关键点数量与邻域内所有关键点数量做比较,获得正确匹配百分比8:将该正确百分比与一固定阈值th(th=50%)作比较,若正确百分比较大,则认为该匹配点对为正确匹配,否则认为其为错误匹配.由此即可判定该匹配点对是否正确9:若还有其他匹配,则取下一匹配判定
1.3 点线距离算法
对图像I1上的待判定点fp与对应图像I2上的匹配点tp,假设fp周围邻域有点a1、b1、c1…k1共k个点,而这k个点在初始匹配中对应于I2上的匹配点为a2、b2、c2…k2,由a1、b1、c1…k1用最小二乘法可以在图像I1中拟合得一条直线L1.同样,由a2、b2、c2…k2也可以在图像I2上拟合得一条直线L2.由于图像变换不改变其线性关系,也就是在I1中为直线,在I2中大致也是直线.如果图像像素没有放大或缩小,那么待判定点fp到直线L1的距离和匹配点tp到L2的距离在理论上应该接近.为了排除图像缩放的影响,我们取fp到L1的距离与a1、b1、c1…k1到L1的平均距离的比值作为相对距离ds1.同样,在图像I2上取tp到L2的距离与a2、b2、c2…k2到L2的平均距离的比值作为相对距离ds2.这样,如果(fp,tp)为正确的匹配点对,那么ds1与ds2应当接近.因此,取|ds1-ds2|作为判定距离,如果|ds1-ds2|大于某个阈值th(实验中th=5效果最佳),那么就可以认为匹配点对(fp,tp)为错误的匹配点对.算法详细描述见算法3.

算法3:点线距离算法输入:两幅图像I1和I2的初始SIFT匹配输出:保留的正确匹配1:选取一对匹配点(fp,tp),并记下其序号.其中fp在I1 中,tp在I2中2:对I1中的每一个匹配点,根据其序号判断该点是否为判定点,若是,则令其对应的距离为无穷大,若不是,则根据SIFT中提取的位置信息计算该点与判定点的欧氏距离.将其欧氏距离记录下来3:将所有有匹配点到判定点的距离都求出后,将这些距离按升序排序4:在图像I1中取出离判定点fp最近的k个点,用最小二乘法将这k个点拟合成直线L1.并求出点fp到直线L1的距离df5:求出fp最近的k个点分别到直线L1的距离的平均值dav6:将df/dav作为fp到直线L1的相对距离ds17:对图像I2中的待判匹配点tp做同样的处理,得到tp到直线L2的相对距离ds28:将|ds1-ds2|作为判定值dj,如果dj>th(th=5),那么认为匹配点对(fp,tp)为错误的匹配点对,将这对匹配点的标志值flag置-1.若dj= 对图像I1上的判定点fp,假设其邻域有2个匹配点a1、b1都是正确的匹配点.而点fp对应图像I2上的匹配点tp,点a1、b1对应图像I2上的匹配点a2、b2,且匹配对(a1,a2)、(b1,b2)均为正确的匹配点对.由此在图I1中可以由点fp、a1、b1构成一个三角形TR1,在图I2中由tp、a2、b2构成三角形TR2.如果(fp,tp)为正确的匹配点对,那么三角形TR1、TR2应当接近相似三角形.通过判定TR1、TR2的相似程度,便可以判定匹配点对(fp,tp)是否正确.为了判定三角形的相似程度,我们记TR1的三边长分别为d11、d12、d13,TR2的三条边边长为d21、d22、d23,在这里取: dj=abs(d11/d21-d12/d22)+abs(d11/d21-d13/d23)+abs(d12/d22-d13/d23)作为相似判定,dj越小,则越相似,(fp,tp)为正确匹配点对的可能性越大. 为了找到判定点fp邻域的正确匹配点对,我们先设计了一个小窗口邻域信息算法寻找正确的匹配点.具体算法为:选取图像I1上的一个点P1,以这个匹配点为中心取一个半径为r(实验中r取50个像素点)的小圆域.圆域内匹配点数大于阈值a(实验中a取15)时令圆域为密集点域,否则为非密集域.在非密集域,匹配点分布稀疏,使用邻域信息算法可能因为匹配点的数量不足导致结果不稳定,邻域相似三角形算法可弥补这一缺陷.使用邻域信息算法,遍历圆域内所有匹配点,得到图像上所有密集点域上的正确匹配点.经过一次判定,可以找到密集点域上比较准确的匹配点.对于密集点域上没有判定的点,其分布类似于非密集域上的点,所以接下来用邻域相似三角形方法判定非密集域上的匹配点和密集点域上没有判定的点. 对于非密集域上的点和密集点域上没有判定的点,我们根据前文所述的相似三角形几何约束设计了相应算法进行判断.假设点M1为非密集点域上的点,取离点M1最近的密集域上的2个正确匹配点F1、T1.M1、F1、T1对应图像I2上的点M2、F2、T2.因此由M1、F1、T1在图I1构建三角形TR1,M2、F2、T2构建三角形TR2,通过三角形相似度判定(M1,M2)是否为正确的匹配点对.该算法的详细描述见算法4. 算法4:邻域相似三角形算法输入:两幅图像I1和I2的初始SIFT匹配输出:保留的正确匹配1:取一对匹配点,获得该匹配在两幅图像I1和I2中的关键点序号(fp,tp)并令fp为待判定点,tp为判定匹配点2:对图像I1上的点判定是否为密集点区域上的正确匹配点 2.1:选取一个圆形区域,这个区域的面积为图像I1的1/k,其半径r可以通过计算得到.然后以I1中的判定点fp为中心,r为半径,统计其周围的点个数m,如果m大于某个值a,则认为此判定点处于密集点域中 2.2:选I1中密集点域中的待判定点fp,其对应于I2中的点tp.以fp为中心,r为半径区域中的m个点,这m个点对应于I2中的 P1,P2,P3…Pm 2.3:以I2中tp为中心,找出离tp最近的m 个点,统计这m 个点与P1,P2,P3…Pm的对应个数,假设这m个点中有b 个点是对应的,如果b/m>=th1(th1为正确匹配点的判定阈值,实验中取50%),则认为这个待判定点fp为密集域上的正确判定点,并将其标志flag置1 2.4:遍历图像I1上所有的待判定点,得到全部的密集区域的正确判定点3:对I1上非密集域上的点和密集点域上的没有判定的点用相似三角形判定 3.1:选I1未判定的待判定点M1,其对应于I2中点M2.找到离M1最近的两个密集域的正确判定点F1、T1,这两点对应I2中的F2、T2 3.2:由M1、F1、T1构建三角形,其边长分别为a1、b1、c1.再由M2、F2、T2构建三角形,其边长分别为a2、b2、c2.对这两个三角形的相似性进行判定.判定值:h=|a1/a2-b1/b2|+|a1/a2-c1/c2|+|b1/b2-c1/c2| 3.3:如果h 基于前文根据四种基本的几何约束设计的误匹配消除算法,我们最后将这四种几何约束方法组合起来进行误匹配消除,组合方式可分为并联式约束(图2)和串联式约束(图3).串联式约束采用每种约束逐步消除误匹配,后面的约束在前面的基础上使用,从而逐渐消除错误匹配.由于各种约束基本上是相互独立的,在去除误匹配的过程中互不干扰,因而串联式约束能够有效融合各种几何约束的优势从而得到最优的误匹配消除效果.如果采用并联的方式,几种约束同时起作用,容易互相干扰反而导致性能下降.并联约束尤其对参数比较敏感,如果参数设置不好,极易将正确匹配点剔除,如果设置过于宽松,剔除的误点数量变少.而串联约束在阈值设置方面,四种几何约束方法的阈值设置较为灵活,即使在最佳阈值上下浮动,仍能比并联式约束更加稳定地剔除误匹配点.后文的实验结果表5也可以证实,并联式组合在设置最佳阈值时虽然准确率比串联式略微高一点,但是由于过滤条件严格导致回响率急剧下降.从理论分析及实验结果综合起来看,串联式组合方式具有更加鲁棒性,因此我们最终选择了串联式组合方式进行误匹配点消除. 图2 并联式约束示意图Fig.2 Paralleling constraint diagram 图3 串联式约束示意图Fig.3 Cascade constraint diagram 采用Mikolajczyk标准数据集[9]来验证本文提出的误匹配消除算法的性能,实验中的图像对均来自该数据集,Mikolajczyk数据集提供每对图像的绝对对应关系,因而可以对匹配结果进行定量的评价.在基本的SIFT匹配中,首先提取两幅图像中的所有SIFT特征点,表示为128维的特征矢量,计算图像对 所有特征点两两之间的欧式距离,对图I1中一个点A,它与图I2中所有的点都有一个距离值,其中来自图I2中距离最小一个点B即为图I1中点A在图I2中对应点,而点A和点B即成为一个匹配点对.为了减少错误匹配,基本SIFT匹配算法要求图I1中的点A在图I2中找到最小距离点B的距离值与次小的距离点C之间的比值要小于某一个阈值,该阈值越小,则要求最小阈值与次小阈值的差异越大,因而匹配的辨识度就越高,这个阈值就称为distRatio阈值.随着distRatio阈值的增大,虽然正确匹配的点数会增加,但是所引入的错误匹配点数也会增加.以表1为例,当distRatio=0.7时,正确匹配的比例是99.39%,当distRatio=0.9时,正确匹配的比例下降到66.49%,大量的错误匹配引入了进来.为了检验算法的容错率,体现算法的鲁棒性能,实验中将SIFT算法中的distRatio取不同的值,得到不同初始匹配率的匹配点. 表1 对不同组别的bark图片进行匹配和剔错的结果Tab.1 The result from matching different group′s bark images and removing false matches 表2 对不同组别的boat图片进行匹配和剔错的结果Tab.2 The result from matching different group′s boat images and removing false matches 表3 对不同组别的bikes图片进行匹配和剔错的结果Tab.3 The result from matching different group′s bikes images and removing false matches 表4 对不同组别的leuven图片进行匹配和剔错的结果Tab.4 The result from matching different group′s leuven images and removing false matches 由上述几组实验可以看出,当SIFT算法的distRatio域值提高时,虽然增加了匹配点对,但是初始匹配点的正确率下降了.本文的串联式约束算法能够剔除绝大多数的错误匹配点,并能保留几乎所有的正确的匹配点.特别是当初始匹配维持在60%以上时,精确率能达到95%左右,回响率在95%以上.例如boat1_3剔除前初始匹配率为69.9%,剔除后达到98.29%,回响率95.24%.该算法有很好的鲁棒性,即使当初始匹配率降到20%,只要适当地调整一级过滤的阈值,就可以使得精确率和回响率都可以保持在80%以上.例如bark1_5剔除前初始匹配率为13.91%,剔除后达到97.73%,回响率82.14%.从以上几组实验得知,本文的串联约束算法可以应付缩放、旋转、光照变化、模糊效应等各种变换产生的错误匹配点.在剔除错误匹配点方面能保持较高的精确率和回响率. 图4 具有很大仿射变换的graf匹配图像Fig.4 Graf matching images with large affine transformation 表5 根据图9匹配然后剔除外点得到的结果Tab.5 The result from matching Fig.9 and then removing its false points 表5为用本文的串联约束算法对图4进行剔除外点后,与其他算法比较的结果.前面的实验结果已经表明,当初始匹配率比较高(一般在60%以上)和匹配点比较多时,本文的串联约束算法与RANSAC、ICF等算法相当.都可以很好地剔除错误匹配点,保持较高的精确率和回响率.在表5中,当精确率下降且初始匹配点稀疏时,本文的串联约束算法仍不如RANSAC、VFC算法.其中的原因主要是本文的算法主要是基于几何约束,这就需要有较高的初始匹配的较多的匹配点作为支撑,特别是初始匹配点数量的减少对本文算法的影响很大.因为本文的算法都是基于邻域得到,当点数量少时,点分布稀疏,本文算法中选取邻域的点在图像上的跨度就很大.对于具有比较大仿射变换的图像(如图4),在本文算法中建立起来的模型就会产生很大的误差,严重影响对外点的正确判断.但是本文中的算法仍有许多有用之处,比如本文中提出了的串联结构剔除误匹配点.由于RANSAC和VFC等算法对剔除错误匹配具有很好的鲁棒性,在以后的精确匹配中,不妨将VFC等具有强鲁棒性的方法作为一次过滤的方法,在滤除掉多数错误匹配之后,再加上精确过滤的方法,如此得到的效果应该会更好. 本文以SIFT匹配为例,主要工作在于剔除错误匹配点.本文给出了4种几何约束,它们分别对应于四种剔除算法:邻域信息算法、方向角算法、邻域相似三角形算法和点线距离算法.为了获得最佳的剔除效果,充分发挥每种几何约束的优势,本文提出了方法的串联式组合方式.本文的算法组合采用了4种方法的结合,但是在很多实际当中,运用2种组合就可以得到满意的结果,只是在有些比较复杂环境下的匹配中运用4种方可更加全面地剔除错误匹配点.本文方法的优点是在外点比例较高的情况下,仍然能获得较高的精确度和回响率.但是本文方法对初始的匹配率有一定的要求,当初始的匹配率在60%以上的时候,方法效果比较优越,但如果初始匹配率太低,则性能退化比较明显.下一步将针对这个问题进行更深入的探讨.1.4 邻域相似三角形算法

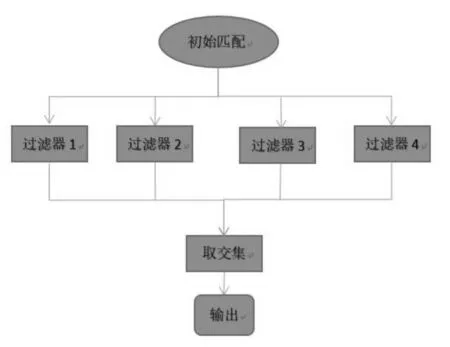
1.5 并联式约束和串联式约束

2 实验结果及分析






3 结语