一种用于多模态心脏图像配准的统计形状模型构建方法

陆雪松，郭翔宇

(中南民族大学 生物医学工程学院，武汉 430074)

多模态医学图像配准在医学图像处理和分析中具有非常重要的意义.不同模态的医学图像在反映人体解剖和功能信息方面具有各自的独特优势，例如计算机断层影像(Computed Tomography, CT)可以提供高分辨率的骨性结构信息，而磁共振(Magnetic Resource，MR)影像在描述软组织解剖和病理结构方面优势明显，单光子发射计算机断层成像(Single-Photon Emission Computed Tomography，SPECT)、正电子发射断层成像(Positron Emission Tomography，PET)等功能影像能够从分子水平上揭示病变组织器官的生理和病理变化，提供更有价值的诊断信息[1].多模态图像融合可以结合不同模态的图像信息为疾病的诊断和治疗策略提供详细而全面的参考依据[2]，精确计算、建模和量化解剖结构信息能够辅助医生制定更合理的治疗方案.多模态医学图像分析方法由于可以多维度、多模式地综合了解疾病动态变化，在指导临床诊断、放射治疗、手术方案制定等方面存在广泛的应用价值.

一般地，配准技术是多模态医学图像融合分析的基础，相似性测度方法[3,4]的选择是决定能否精确配准的关键因素.传统的互信息(Mutual Information，MI)方法旨在寻找图像间的灰度统计关系，已被广泛应用于多模态图像配准过程.但是，它并不是一个凸函数，容易陷入局部最优造成错误对齐的风险.为了克服上述缺陷，许多研究者对其进行了改进.ZHUANG等[5]利用空间位置编码互信息，用于心脏磁共振图像的配准.WOO[6]等提出三维Harris算子结合空间和几何信息的多模态配准方法，用于高低分辨率图像间的配准，相较于传统的配准方法获得了更好的精度和性能.LIU等[7]提出了一种基于深度全卷积网络的多模态图像配准框架，该框架结合了深度FCN模型和单模态配准方法，通过大量可训练的参数自动捕获不同模态间的复杂非线性关系，实现了快速、稳健的多模态医学图像配准.朱飞[8]提出由自相似性激发的Zernike矩描述子，用于非刚性多模态医学图像配准.该方法从图像表征的角度入手，构建熵图表征不同模态图像的特征信息参与配准过程，在准确性和鲁棒性都较目前主流的基于图像表征的配准方法有了大幅度的提升. SIMONOVSKY[9]等提出一种基于卷积神经网络的深度相似性度量方法，并将该方法用于多模态医学图像配准过程，获得了优于互信息的配准结果.

目前，多模态心脏图像配准已经被用于心脏结构的量化评估、心脏病的诊断和手术中.SHI等[10]对标记和未标记MR图像进行非刚性配准，为心脏功能评价中的心肌运动跟踪提供帮助.ZHUANG等[11]在非刚性配准的基础上，采用多尺度信息计算多模态图谱之间的相似性，从而提取心脏子结构，辅助心脏病的早期诊断.TAVARD等[12]提出多模态心脏数据配准和融合的工作流，对心脏再同步治疗实施优化.最近，日趋成熟的形状建模技术也已被用于心脏的分割和配准中.ZHENG等[13]使用基于B样条的统计形变模型编码目标解剖结构的先验信息，利用该先验信息约束2D-3D配准过程，减少了优化所需的参数数量.BERENDSEN等[14]提出使用一系列分割好的目标形状训练获得其统计形状信息，并基于该先验信息作为正则项引入到自由形变配准框架，减少局部极值和错误对齐，获得了更好的配准质量和效果.

本文主要针对多模态心脏图像的配准问题，提出了一种统计形状模型(Statistical Shape Model，SSM)构建方法，并将左心室的统计形状模型作为先验约束项引导多模态心脏图像的配准过程.本文呈现的统计形状模型构建方法主要通过一系列图谱标签图像建立目标形状样本训练集，利用等值面提取算法获得特征点代表目标形状，在确立图谱标签图像之间的形变关系基础上对齐形状特征点，最终结合统计学方法获得样本形状的统计学信息.

1 基于点分布的左心室统计形状模型

在临床上，左心室功能参数的定量分析对诊断和治疗心脏疾病具有重要的价值.近些年来，许多新的方法被提出用于获取左心室功能参数，如形变模型、统计形状模型和多图谱分割等.其中，统计形状模型作为一种强先验模型效果非常显著.作为统计形状模型之一的点分布先验模型，其主要思想是从训练集标签图像中提取一系列特征关键点，用其坐标构成的特征向量来描述目标形状，通过对样本形状训练获得目标形状的统计信息，据此建立坐标特征向量表征形状模型.

假设{xi;i=1,…,n}代表n个左心室样本形状，每个形状包含m个3D坐标点，{pi=(xi,yi,zi)T;i=1,…，m}表示样本形状表面三角剖分的网格顶点，则每个左心室形状向量xi的大小为3m维，构成的坐标点集向量为p=(x1,y1,z1,x2,y2,z2,…,xm,ym,zm)T.假定所有形状的坐标点位置统一于同一坐标系下，则训练集中的各个左心室样本形状向量构成一个三维空间分布，该分布可以用一个线性模型近似表征，表示形式如下：

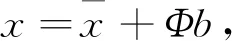
(1)

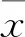
(2)

(3)

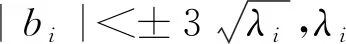
统计形状模型的构建源于训练集标签图像，训练集中的每一幅标签图像代表一个解剖结构的形状实例.由于训练集样本标签图像源于不同灰度图像对同一目标解剖结构的手动分割结果，样本形状变化存在很大的任意性，无法满足建立统计形状模型对样本数据集的要求.因此，需要去除其非形状因素的影响，在不改变模型特定形状的前提下，将训练集样本形状统一于同一模板框架下，使得样本形状能够围绕同一个中心在特定范围内变化.为了使左心室训练集样本形状都处于同一坐标空间中，可基于左心室模板图像建立自然坐标系，在该坐标系下形变图谱训练集样本形状，最小化不同样本形状间的形变影响.建立自然坐标系的目的是将样本形状对齐并归一化于模板形状所在的自然坐标空间中，该目标的实现主要通过配准找到模板框架与图谱图像间的对应关系.

理想情况下，可以使用解剖学特征点描述目标解剖结构的形状.然而，由于解剖学特征点过于稀疏，无法准确描述其三维形状，可采用表面特征点来确定其几何形状，通过坐标向量对目标形状进行表征.为了提取左心室图谱样本形状特征点，首先需要对模板图像进行标记，然后再通过非刚性配准所获得的变换参数实现模板图像和图谱图像间形状特征点的自动传递.为了自动标记左心室模板图像形状特征点，等值面提取算法(Marching Cube，MC)被选择用于该过程.等值面算法可生成目标形状表面密集的三角剖分网格，从生成的网格模型中提取其表征形状模型的坐标特征点作为特征描述符.由于该算法应用于模板标签图像后，生成的网格节点数目过多，选用稀疏抽取技术降低特征标记点的数量，同时保留尽可能好的形状和拓扑结构.左心室形状特征点的自动标记框架如图1所示.

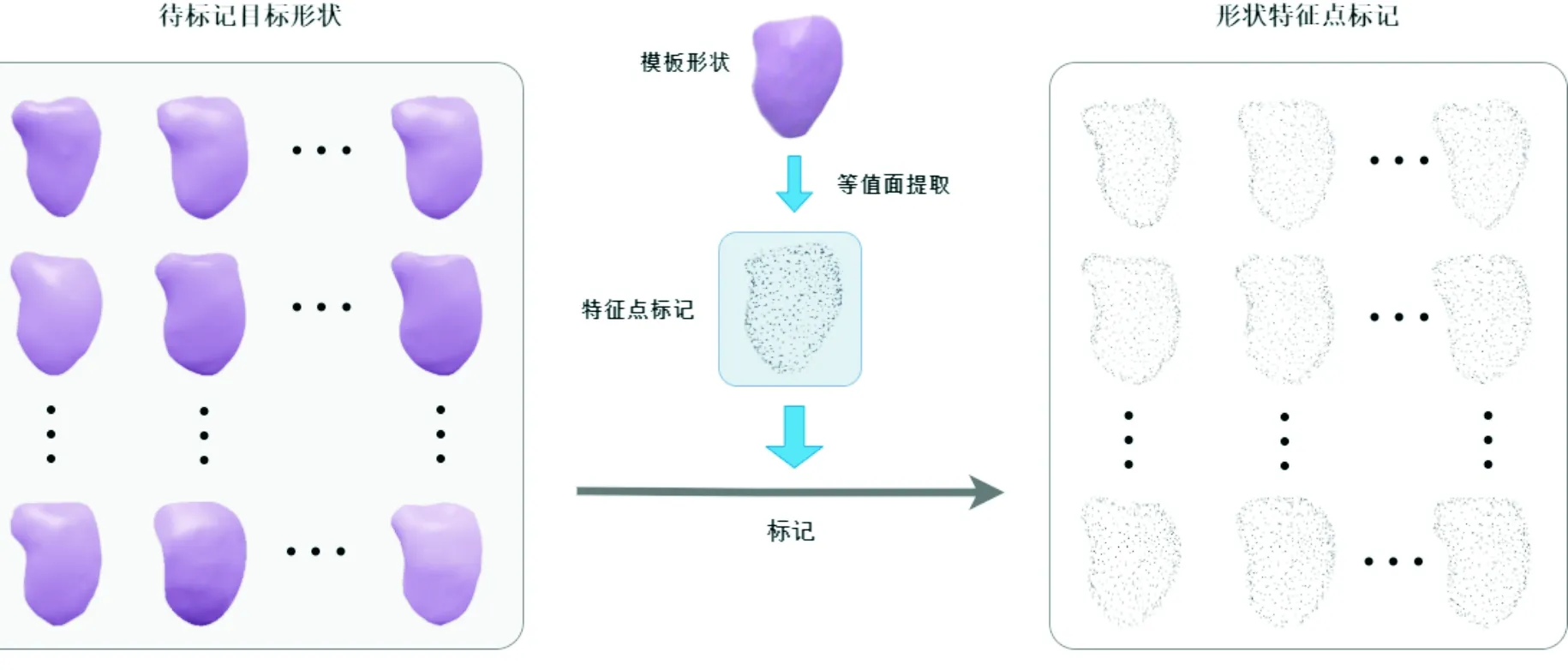
图1 形状特征点自动标记示意图Fig.1 The automatic landmark diagram of shape feature points

2 左心室统计形状模型具体构建流程

假定训练集Sn由n个左心室标签图像构成，训练集中的每个形状通过标签图像的前景像素值描述.为了生成n个左心室形状的特征标记点，应选择一幅标签图像作为模板标签图像，提取其形状特征点，并利用该模板标签图像标记的形状特征点通过训练集配准框架实现其余n-1个左心室形状的自动标记，最终结合统计学方法获得目标形状的统计信息，依据统计信息计算其均值特征向量和协方差估计矩阵完成整个左心室统计形状模型的构建.左心室统计形状模型的具体构建流程如下：

Step1 从给定的训练集Sn中确定一幅标签图像作为模板标签图像；

Step2 该模板标签图像对应的原始灰度图像作为模板图像，其余n-1幅标签图像对应的灰度图像作为图谱图像，通过全局仿射变换将所有图谱图像统一于模板图像所在的自然坐标空间中，迭代计算模板图像和图谱图像间的形变配准参数；

Step3 将Step2计算获得的形变配准参数应用于对应的图谱标签图像，形变生成其统一于同一自然坐标系下的图谱标签图像，构建图谱样本形状训练集；

Step4 取训练集中的每一幅图谱标签图像分别与模板标签图像做形变配准，配准的相似性测度方法选用Kappa统计系数，使参与配准的两幅标签图像的重叠率最大，迭代该过程计算其形变配准参数；

Step5 使用等值面算法对模板标签图像形状实施自动标记，提取形状特征点并生成对应的形状描述点文件；

Step6 通过Step4计算得到的形变配准参数，建立模板形状和待标记(图谱)形状间的点对应关系，将Step5获得的模板图像形状标记点映射到待标记图像中，提取坐标生成相应的形状点描述文件；

Step7 根据Step6计算获得的一系列形状标记点描述文件，结合统计学方法构建n-1幅图像的形状统计信息，最后计算其均值特征向量和协方差估计矩阵.

本文以双源CT采集的300个心脏三维图像为实验数据集，在该数据集上通过手动分割左心室结构获得标签图像，遵循上述方法和具体流程，构建样本形状训练集，生成左心室统计形状模型.

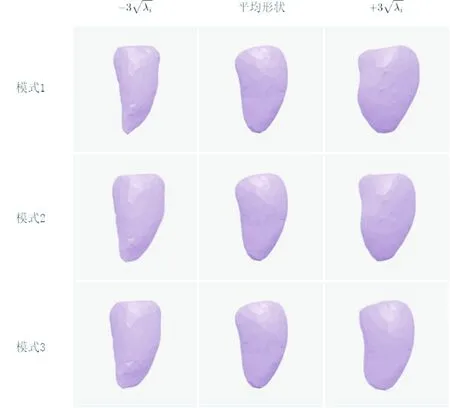
图2 不同模式下模型的变化效果Fig.2 The effect of the model in different modes

图2是利用该CT数据集建立的左心室形状模型在不同模式下的变化效果.

3 基于统计形状模型约束的多模态心脏图像配准

医学图像配准的实质是寻找图像间的最优变换使得其目标代价函数最小，传统的医学图像配准方法使用互信息作为代价函数计算其最佳变换参数.为获得高精度的配准结果，本文采用统计形状模型约束互信息度量引导配准寻优过程，其代价函数如下所示：

C=-S+αR,

(4)

式中S互信息测度函数，R为形状先验约束项，α为平衡代价函数中两项测度贡献的权重因子.

通常情况下，依赖于B样条的自由形变配准使用基于梯度下降的方法迭代求解代价函数的优化问题.类似的，形状先验约束项R的梯度应与形变参数有关.假设参考形状特征向量为Pref，平均形状向量为Pmean，形状先验约束项R可通过Pref和Pmean间的马氏距离表示：

(5)

式中P(μ)为变换后的参考形状向量与平均形状向量的差值，可表示为：

P(μ)=Tμ(Pref)-Pmean,

(6)

因此，参考形状向量和平均形状向量间的马氏距离与其配准变换参数μ相关.形状先验约束项相对于变换参数的梯度为：

(7)

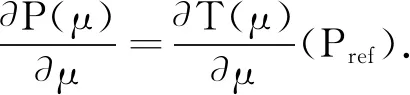
基于统计形状模型约束的多模态心脏配准在CT与MR图像间进行，参与配准的测度方法使用上述公式(4)定义的目标函数，而最优空间变换参数的获取是通过迭代优化的搜索策略计算其梯度进行确定，该值越小，则互信息相似性度量值越大，配准参数越接近于最佳值.为了更快、更准确的达到最小值完成配准任务，一般使用梯度下降的方法求解该计算过程.

4 实验结果与分析

为了验证模型构建的准确度和配准方法的有效性，本文实验在基于ITK(Insight Toolkit)框架的开源配准工具包Elastix[15]上实现.实验数据集选择双源CT采集的心脏影像和磁共振采集的心脏MR影像[16]，利用该CT数据集建立左心室统计形状模型，并基于该模型进行心脏的多模态配准实验验证.该CT影像数据集来自15位病人，每位病人有20幅心动周期图像，图像的分辨率为512×512×117～265，像素尺寸0.28 mm×0.28 mm×0.5 mm～0.37 mm×0.37 mm×1.0 mm. MR图像的分辨率为288×288×120～512×512×200，像素尺寸0.78 mm×0.78 mm×0.89 mm～1.11 mm×1.11 mm×1.60 mm.临床医生手动分割的左心室结构被看作为金标准.

在该15×20幅心脏CT图像上建立左心室统计形状模型，执行步骤遵循上述的具体构建流程.实验采用leave-one-out策略共建立15个左心室形状模型，每位病人的第一幅心动图像作为模板图像，剩余14位病人的所有心动图像作为图谱图像.完成每个形状模型需进行14×20次配准，其中先经过仿射配准使图谱图像归一化于模板图像所在的自然坐标空间中，计算形变图谱标签图像，然后采用Kappa统计作为相似性测度对标签图像进行非刚性配准，最后根据该形变场建立模板形状和待标记形状的点对应关系，提取形状特征点并计算其均值和协方差获得统计形状模型.

选择15组心动周期的第一幅CT图像和MR数据集中的20幅图像进行多模态配准验证实验.其中CT图像作为模板图像，MR图像作为图谱图像，共进行15×20次配准.为了对配准的结果进行评估，配准实验建立了以传统的互信息(MI)配准方法为基线，和引入统计形状模型(MI+SSM)的配准方法进行对比验证.通过配准结果形变场，将图谱图像的左心室手动分割结果进行形变，可作为模板图像的自动分割结果.配准结果的精确性度量选择模板图像中左心室自动分割结果与金标准之间的体积重叠率(Dice Similarity Coefficient，Dice)系数进行测量.二者重叠率DSC值在0～1之间，重叠率越高，表明配准的精度越好.整体配准实验结果如表1所示，分别比较了MI和MI+SSM方法的多模态配准精度.

表1 两种方法配准结果重叠率比较
Tab.1 The comparison of overlap rate from registration results using two algorithms

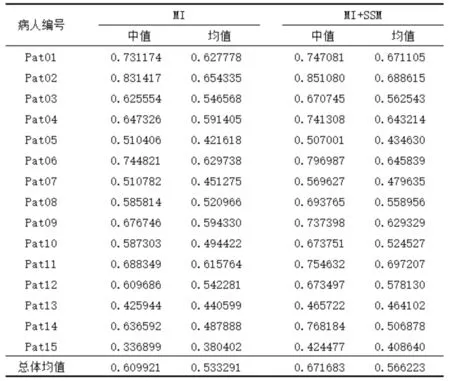
由表1的实验数据可见，引入统计形状模型的配准方法较传统的互信息法有了明显的提高，配准精度的中值和均值分别提高了0.06176和0.03293.由此可知，引入统计形状模型的配准方法性能较优，证明了模型构建方法的有效性.为了进一步对本文提出的构建统计形状模型的方法和建立的模型质量进行评估，图3显示了三个病例的左心室自动分割结果和金标准对比.，图中第一列红线框定的区域为左心室结构的金标准形状，第二和第三列框定的区域分别为互信息和模型约束的配准方法获得的左心室配准结果，根据图示结果可知，经过SSM配准的结果相较于MI的方法左心室目标形状的差异较小，更加接近金标准.

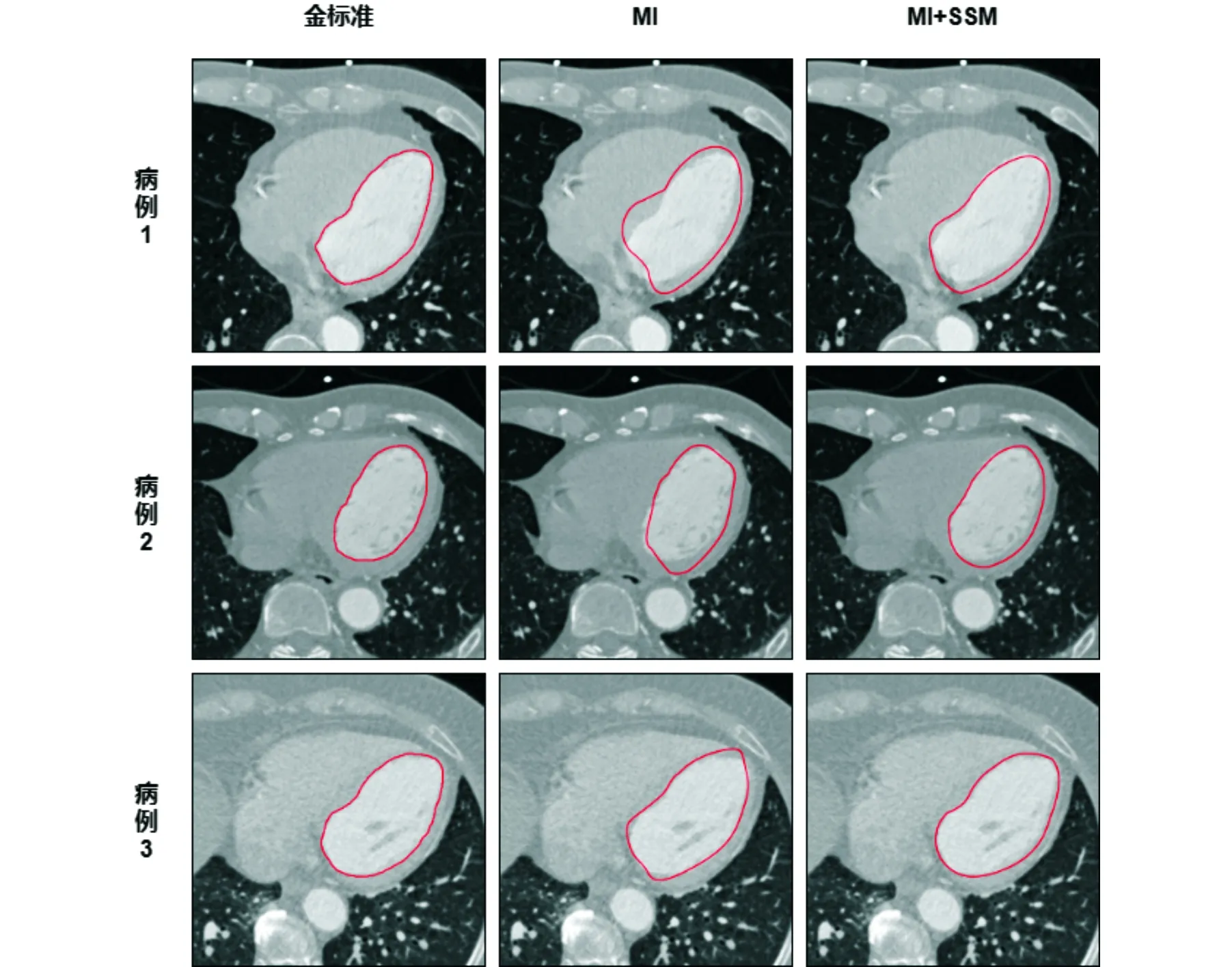
图3 两种方法的左心室实际配准结果对比Fig.3 The comparison of registration effect using two methods

5 结语

统计形状模型构建的关键在于训练集样本形状的构造和坐标标记点的自动提取，模型的表达通过均值特征向量和协方差矩阵进行描述.本文提出的统计形状模型构建方法使用仿射和B样条自由形变模型相结合的方式构建图谱样本形状训练集，利用等值面提取算法完成形状特征点的自动标记过程并对坐标点进行提取，最终结合统计学的方法计算均值特征向量和协方差矩阵表征形状模型.为验证本文论述模型构建方法的准确性和有效性，采用CT和MR图像进行多模态配准实验.结果表明，本文所采用的模型增强的方法较传统互信息方法在多模态配准左心室精度上有较大提升，说明了本文提出的统计形状模型的构建方法具有可操作性和实际意义.