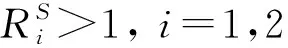具有Beddington-DeAngelis发生率的随机SIQS双流行病模型的动力学研究
2020-02-08韦煜明彭华勤
吕 杰,韦煜明,彭华勤
(广西师范大学数学与统计学院, 广西 桂林 541006)
传染病历来是危害人类健康的大敌, 为寻求对其预防和控制的最优策略, 建立能反映传染病动力学特性的数学模型, 通过对其定性、定量分析和数值模拟, 来显示疾病的发展过程和传播规律[1]. KERMACK和MCKENDRICK提出了均匀混合原则[2], 从而建立了现在熟悉的仓室模型, 并得到了广泛的应用. 许多研究人员在传播和控制传染性疾病方面取得了显著进展, 如麻疹, 鼠疫, 水痘, 天花, 结核病, 肝炎等传染病[3-5]. 在疾病发生时, 为了减少受感染人数, 政府或组织通常会采取隔离措施. 此时的生物数学模型称为SIQS流行病模型[6]:
其中,S表示易感人群数量,I表示受感染但未被隔离数量,Q表示受感染后被隔离数量,Λ为新进人口数量,μ表示自然死亡率,γ,ε分别表示受感染个体和被隔离个体的恢复率,α表示因病死亡率,β表示接触率,δ表示已受感染个体的隔离率.
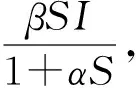
基于以上模型分析, 提出具有Beddington-DeAngelis发生率的双流行病SIQS模型:
(1)
其中I1,I2表示被A病毒和B病毒的感染者数量,β1,β2分别为2种疾病的接触率,γ1,γ2分别为2种疾病的恢复率,ai,bi(i=1,2)为抑制效果参数,δ1,δ2分别为已受感染个体的隔离率,α1,α2,α3分别为2种疾病在I1,I2,Q中的因病死亡率,γ1,γ2,ε分别为2种疾病在I1,I2,Q中的恢复率.考虑到自然界的不确定性和随机性, 许多学者提出了将随机扰动引入微分方程的方法来揭示环境波动的影响[14].考虑由于环境波动和随机扰动的强度, 假设因病死亡率和发生率在平均值上下波动, 本文提出随机SIQS双流行病模型:
(2)
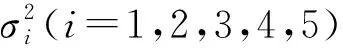
本文第1部分将证明系统(2)的全局正解的存在和唯一性; 第2部分将分析疾病的灭绝性; 第3部分研究了一种遍历平稳分布的存在, 即疾病将在人群中流行, 不会灭绝; 第4部分将总结本文的主要结论并给出数值模拟.
1 全局正解的存在和唯一性
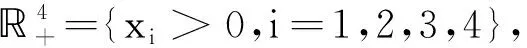
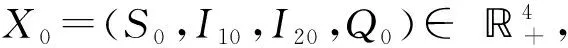
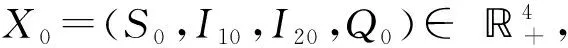
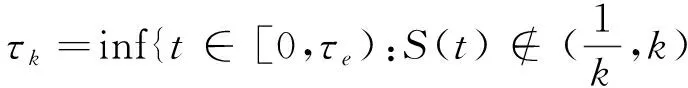

σ1(I1-1)dB1(t)-σ2(I2-1)dB2(t)-σ3(Q-1)dB3(t),
其中K为正整数, 则有
σ2(I2-1)dB2(t)-σ3(Q-1)dB3(t),
对上式两边同时从0到τk∧T积分, 并求期望:

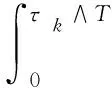
即
E(V(S(τk∧T)),I1(τk∧T),I2(τk∧T),Q(τk∧T)))≤
E(V(S(0),I1(0),I2(0),Q(0))+KE(τk∧T)≤E(V(S(0),I1(0),I2(0),Q(0))+KT.
(3)
令Ωk={τk:τk≤T}, ∀k≥k1, 有P(Ωk)≥. 对∀ω∈Ωk, 则至少存在一个S(τk,ω)或者I1(τk,ω) 或者I2(τk,ω)或者Q(τk,ω)等于k或等于即
由式(3),
V(S(0),I1(0),I2(0),Q(0))+KT≥
E(IΩk(ω)V(S(τk∧T),I1(τk∧T),I2(τk∧T),Q(τk∧T))≥
其中IΩk(ω)是示性函数, 当k→∞时∞>V(S(0),I1(0),I2(0),Q(0))+KT=∞,矛盾, 故有τ∞=∞,得证. 即存在全局唯一正解.
2 疾病的灭绝性
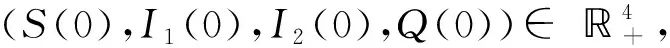
证对系统(2)应用It公式可得
(4)
两边同时求积分并除t可得
同理, 若H(σ2,σ5)<μ+α2+γ2+δ2, 那么系统(2)的疾病B将会灭绝.
由定理2可知,相对大的噪音强度会促使疾病灭绝.
3 系统的平稳分布和遍历性
本节主要讨论系统(2)的2种流行病的持久性, 对于确定性模型, 此问题常通过给出有病平衡点是一个全局吸引子或是全局渐近稳定的来解决, 但随机系统(2)不存在有病平衡点, 故本节应用KHAS’MINSKII[15]的平稳分布, 反映疾病是否流行.
引理1[15]Markov过程X(t)存在平稳分布π(·),f(·) 为关于测度π可积的函数, 对∀x∈n, 如果存在具有正则边界Γ的有界区域D⊂n且满足:
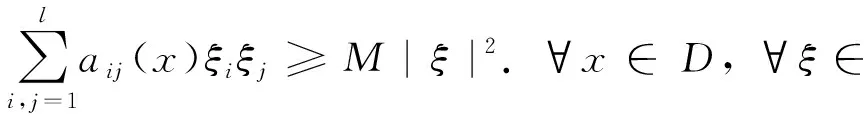
(ii)存在非负C2函数, 使得对∀x∈nD,LV是负的,其中:
定理3假设
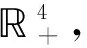
证若要证明定理3, 只需证明引理1的2个条件满足.

V(S,I1,I2,Q)=p1(-lnS-c1lnI1)+p2(-lnS-c2lnI2)+(S+I1+I2+Q)ρ+1-lnS-lnQ:=
p1V1+p2V2+V3+V4+V5,
其中:
常数p1,p2,ρ满足以下条件:
(6)
(7)
(8)
其中:
LV3=(ρ+1)(S+I1+I2+Q)ρ(Λ-μS-(μ+α1)I1-(μ+α2)I2-(μ+α3)Q)+
其中:
故
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
当ε2,ε3充分小的时候, 由条件(6)可得条件(10), 由条件(7)可得条件(11).有
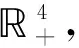
(A1) 当(S,I1,I2,Q)∈D1时, 应用条件(9)可得
(A2) 当(S,I1,I2,Q)∈D2时, 应用条件(10)可得
(A3) 当(S,I1,I2,Q)∈D3时, 应用条件(11)可得
(A4) 当(S,I1,I2,Q)∈D4时, 应用条件(12)可得
(A5) 当(S,I1,I2,Q)∈D5时, 应用条件(13)可得
(A6) 当(S,I1,I2,Q)∈D6时, 应用条件(14)可得
(A7) 当(S,I1,I2,Q)∈D7时, 应用条件(15)可得
(A8) 当(S,I1,I2,Q)∈D8时, 应用条件(16)可得
(ii)系统(2)的扩散矩阵为
4 数值模拟
用Milstein方法[17]来验证所得主要结果的有效性, 并总结本文的重要结论. 首先将模型(2)离散化
其中ξi(k)(i=1,2,3,4,5,k=1,2,3,…,n) 是服从N(0,1) 分布的独立的随机变量.
4.1 疾病的灭绝性
首先当系统(2)中σ1=σ2=σ3=σ4=σ5=0 时为SIQS确定性模型, 即不受环境干扰的情况, 取参数Λ=1,μ=0.1,β1=0.5,β2=0.7,γ1=0.1,γ2=0.1,δ1=0.1,δ2=0.2,α1=0.1,α2=0.2,α3=0.2,a1=1,a2=1,ε=0.1,b1=2,b2=1, 确定性模型随时间t变化的趋势如图1.
由定理2可知, 当H(σ1,σ4)<μ+α1+γ1+δ1且H(σ2,σ5)<μ+α2+γ2+δ2时, 2种疾病消亡. 如图2, 给定的初值为(S(0),I1(0),I2(0),Q(0))=(10,5,5,5). 此时选取受环境扰动的参数值分别为:σ1=0.1,σ2=0.2.σ3=0.1,σ4=0.5,σ5=0.5. 满足条件H(σ1,σ4)<μ+α1+γ1+δ1,H(σ2,σ5)<μ+α2+γ2+δ2.

图1 确定性系统(S,I1,I2,Q)的轨迹 Fig.1 The paths of S, I1, I2 and Q for the determin-isticmodel 图2 随机系统(S,I1,I2,Q) 在σ1=0.1, σ2=0.2, σ3=0.1, σ4=0.5, σ5=0.5下的轨迹Fig.2 The paths of S, I1, I2 and Q for the stochastic modelwith noise intensities σ1=0.1, σ2=0.2, σ3=0.1,σ4=0.5, σ5=0.5
4.2 疾病在均值意义下的持久性
由定理3可知:
由图6可知, 系统(2)存在唯一的遍历平稳分布, 即图5和图6都可验证系统(2)中2种疾病在此状态下持久.
5 主要结论