改进课堂复习方式，促进学生深度学习

朱艺峰

摘 要：复习课在注重回顾基本知识，训练基本技能的同时，应从核心素养的视角，立足学生思维能力的发展。复习教学不应以重复训练为导向，而是要引导学生用数学的眼光看待问题，会用数学的思维研究问题，会运用所学知识分析问题和解决问题，以提升学生综合的学习的能力。本文以几何章节课复习课的设计为例，整合已有的资源，拓展提炼，激发学生思考的欲望及再次学习探索的积极性，促进学生知识网络的建构与生长。

关键词：复习;思维;深度学习

一、问题的提出

（一）复习课的意义

复习就是把学过的知识再学习。俗话说“温故而知新”，只有通过对旧知的整理巩固，才能作为新知的生长点，从而促进学生对新知的掌握、理解和运用。

复习课是在课堂中把已学过的知识系统化的教学活动。一堂好的复习课，教师应该以学生为中心，根据学情设计出合理高效的复习方式，为学生构建合理的复习情境，引导学生找出知识间的联系，学会分析综合，建立知识体系，从而加深对知识的理解，促进对知识的消化吸收。

复习课根据复习的时间和内容，可分为章节复习，专题复习和阶段性复习，本文所探讨的复习课，专指的是章节复习课的设计。章节复习课可以是学生在刚学习新课后进行，也可以是在总复习中进行，形式多为对知识的总结归纳，以帮助学生梳理本章中各知识点之间的联系，为学生构建知识导图。它不同于专题复习的深入性，也不同于阶段性复习的综合性，它的重点应该是梳理知识，传达的数学思想就是化归，目的就是让学生找到零散知识点之间的联系，学会把新的、难的问题转化为旧的、易的问题，提升认知的高度，提高数学素养。

（二）深度学习的意义

深度学习的概念来源于人工神经网络，是希望机器能像人一样具有分析能力。而我们所说的深度学习，是一种积极主动的学习过程，学生能将所学的知识运用到真实的生活情境中，在具体的学习过程中实现思维的提升。这样的学习方式，内驱力来源于自身，学生能全身心的积极参与，并能体验到成功的喜悦。

本文展示的几个几何章节复习课的案例设计，都是在教师的引导下，学生围绕具有探索性的学习主题，自主提出问题，并通过合作探究来解决问题。此类复习课教学设计关注的是学习内容的本质及其潜在含义，学生通过学习既能掌握关键概念，又能了解各部分知识之间的联系，学生的学习动机是和内在愿望紧密联系在一起的，使学生获得最佳的复习效果。

二、现状分析

（一）复习课变成了习题课。教师经常使用题组、变式训练，主观的认为在帮助学生归纳整理，但实际课堂中就是一个做题讲题的流水线工程。

（二）教师帮学生回顾所学知识。原意是帮助学生整理归纳，但实际课堂中就是背诵知识点的比拼，学生不仅仍然不会梳理、归纳，更不用说是知识的总结、应用和能力的提升。

（三）教学设计没有尊重学生的认知水平。主要就是忽视学情，有些课堂中明明学生都已掌握的还在复习，有些课堂复习之后学生还是完全不会。

（四）教师不能准确把握知识之间的联系。在大多数复习课中，教师往往缺乏对解题的总结、提炼，没有帮助学生养成及时梳理总结的好习惯。

为了帮助学生亲身经历知识梳理、自主建构知识网络的过程，我们教师的复习课堂必须

立足课标，从学生原有的认知水平和知识经验出发，设计合理而高效的复习方式，让所有学生都能通过学习，实现由“量”到“质”的提升。

三、案例展示

例1：全等三角形的复习课

【教学目标】1.通过不同方法画全等三角形，巩固全等三角形的判定方法。

2.通过全等画法的思维发散，寻找知识间的联系，构建知识体系。

3.培养学生观察和动手能力及发现问题的能力，学会运用已有的知识分析解决新的问题，提升学生的数学素养。

【教学设计】

传统的课堂复习课都是老师归纳，学生机械的听讲，或者老师出题，学生解题，对于学生的学习都是停留在浅表层的，如果想要改变学生的学习深度，必须要让学生高度的参与到教学活动中来，而让学生感兴趣的课堂教学模式就是让学生动起来。本节课作者摒弃了图表式的归纳，选择了适合学生认知规律和个性特征的素材作为课堂的切入口，在作图的过程中，既对知识进行了归纳总结，也对知识间的关系作了梳理，充分调动了学生学习的积极性，开发了学生的思维。

环节一：用你手上的作图工具（刻度尺、圆规、量角器、三角板等）画一个三角形全等于已知三角形。（用尽可能多的方法来画图）

学生解答：

老师提问：这几位同学的方法非常棒，那么请问，他们分别是利用了什么原理来画的图呢？

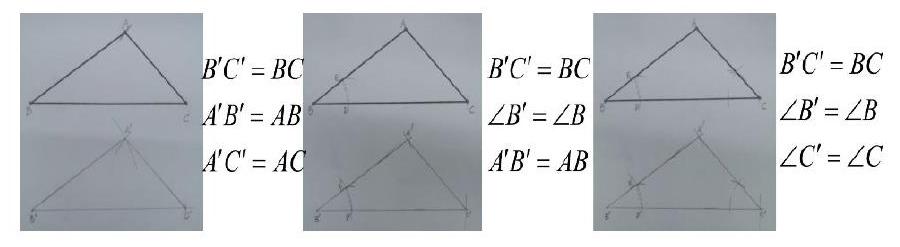
学生一：画法①是利用SSS全等的方法来画图的;画法②是利用SAS全等的方法来画图的;

画法③是利用ASA全等的方法来画图的;老师提问：我们的同学们通过SSS，SAS，ASA来画全等的三角形，正是利用了全等的三种判定方法，对不对？那么在画图的过程中，老师又产生了一个问题，想请同学们帮忙解答一下。在画法2和画法3中，都利用了角的元素，那么请问，如果只用尺规画一个角等于已知角，我们又是利用了什么原理？

學生陷入沉思，在大脑中拼命思索之前学习画一个角等于已知角的过程，好像就记得怎么画了。不过也有一些同学想起之前这节课的过程，老师在引导学生如何画的过程中，解释过为什么，也总结过原理。

学生：我们可以根据画法来分析，1、画一条射线，以B为圆心，适当长为半径画弧，交BC、BA于D、E两点;2、再以B为圆心，同样长为半径画弧，交射线于点D，得到BD=BD;3、以D为圆心，DE长为半径画弧，两弧交于点E，利用DE=DE;4、连接BE，此时BE=BE.所以我认为这里的依据是三边相等。

老师归纳：这位同学分析的很到位，我们在用圆规作一个角等于已知角实质上也是在利用了SSS全等，因为圆规它的功能归根到底就只有截取和度量的功能，所以都是线段的关系。这种推断我们可以用到以后的作图原理中，不管我们利用圆规作了什么，利用的都是线段相等的条件。

老师追问：除了以上三种方法，还有其它方法可以画全等的三角形吗？

学生四：还可以利用AAS来画。不过这个画图的过程比较复杂，需要转化下角，实际上也是利用了ASA的判定。

学生五：我可以用其它的方法来画。1、在原三角形中作高;2、画一条边等于底边，然后在同样的位置做高;3、连接。

老师归纳：这几位同学又给了我们非常好的思路。那么请问，大家能发现他们在作图时的依据吗？

学生：画法6我认为是利用了平移的性质。画法7应该是轴对称变化。画法8就是旋转变化。

老师追问：大家说这位同学说的对不对？我们除了可以利用全等的判定方法来判定三角形全等，同样还可以通过图形的变换来构造全等三角形。那么请问在作图的过程中，我们又是利用了它们的哪些性质呢？

学生：这三种变化都不改变原图形的形状和大小，所以变换前后的图形都是全等的。平移可以利用推平行线的方法作图，轴对称可以利用对称轴作图，而选转变化中利用的是最特殊的中心对称（旋转180°角）方法来画的图。

教师归纳：这节课我们通过作图復习了全等三角形，同学们能否用一张图来归纳下？

例2：特殊的平行四边形复习课

【教学设计】

特殊的平行四边形是我们在学习了平行四边形之后接触到的，本章的三种特殊图形，其实研究的过程正好展示了我们研究平行四边形的一般思路，从边到角，再到对角线。本人没有通过传统的变式教学，是不想学生因为解题而解题，而是要让学生学会自己分析问题，自己研究问题，想教会学生一种思考的方法。另一方面也是想让学生能够学会整理一章或者某一个知识板块的方法，只有学生心理有了整体的概念，才会对问题有清晰的认识，这对于九年级的总复习做了一些铺垫。

本章的复习是建立在平行四边形这章的学习上，虽然对于平行四边形的性质与判定学生基本已经比较清晰，但学生的心理还是没有整个板块的学习框架或者整理的方法，希望通过本节课的整理与归纳，让学生对于性质及判定的掌握能够更深入，并能够理清四边形之间的关系，对于他们复习其它几何图形也是一种借鉴。

环节一：如图，在四边形ABCD中，E、F、G、H分别是边AB、BC、CD、DA边的中点，请判断四边形EFGH的形状，并说明理由。

改变问题中划线部分的条件，变成新的问题，画出图形，得出结论并证明。

学生通过把四边形改成平行四边形、矩形、菱形及正方形，来判定新的特殊四边形。

【设计意图】此过程中，从四边形到平行四边形，既是复习前一章的知识，也为特殊平行四边形的复习做了铺垫。通过改变条件，让学生经历从一般四边形到特殊四边形的思考过程，形成初步的知识框架。通过探索并归纳出几何图形中各元素之间的关系，得到一般地研究方法。

环节二：在平行四边形ABCD中，①E、F分别为BC、AD的中点②AB⊥AC③AB=AC

选择以上①②③中的若干个作为条件，编一个题目，写出已知、求证并证明。

学生1：选择①，连接EF，得到平行四边形ABEF和平行四边形DCEF。也可连接AE，CF，得到平行四边形AECF。（平行四边形的性质与判定的综合运用）

学生2：选择①②得到AECF是菱形（利用对角线互相垂直或者一组邻边相等判定）

学生3：选择①③得到AECF是矩形（利用对角线相等或者有一个角是直角判定）

学生4：选择①②③得到AECF是正方形（综合菱形和矩形的判定方法）

【设计意图】此过程，给出几个条件，让学生自由组合，是检验学生是否掌握了研究特殊四边形的一般方法，并能够以此得到提升。本人没有通过传统的变式教学，是不想学生因为解题而解题，而是要让学生学会自己分析问题，自己研究问题，想教会学生一种思考的方法。另一方面也是想让学生能够学会整理一章或者某一个知识板块的方法，只有学生心理有了整体的概念，才会对问题有清晰的认识，如此设计侧重于思维方面的回顾与整理，注重培养学生思维的发展和延续。

环节三：梳理知识

【设计意图】学生在黑板上的展示过程，通过板书的设计，得到整章的思维导图，让学生对于特殊的平行四边形之间的关系有整体的概念，便于解决各种问题。通过探索并归纳出几何图形中各元素之间的关系，得到一般地研究方法。

例3：圆的基本性质复习课

【教学目标】

1、通过尺规作图画一个等弧，引导学生复习圆中各元素之间的等量关系。

2、在建立知识框架的同时，指引学生从弧的角度去探究问题，给学生解决问题开辟了新的路径。

3、学生自己动手操作改变了原有枯燥的复习课模式，启发学生深度思考，提升学生的思维层次。

【教学设计】

环节一：画一段弧等于已知弧。

学生解答：

教师：这四种画法是我看到的最多，也是画的最快的，请同学们分别说说大家画图的依据。

学生：（图一）∵AB=CD∴AB=CD;（图二、图三）∵∠AOB=∠COD∴AB=CD;

（图四）∵∠ACB=∠BCD∴AB=CD

教师：除了上面四种画法，我还看到了其它的几种画法，我们请同学们也来说说看画图的依据。

学生：（图五）∵DE=DF∴AB=CD∴AB=CD（图六）

∵OA⊥BC∴BD=CD∴AC=BC

教师：同学们分析的都非常正确，我们可以把这集中画法归纳下：

教师：老师这里还有一种画法，不知道大家能不能看出它的依据是什么？

学生：这个好像和图六的依据是一样的，只是在画垂直的时候和前面有所区别，这里是根据直径所对的圆周角是直角来画垂直的。

∵BD⊥OA∴BC=CD∴AB=AD

环节二：画一段弧等于已知弧的两倍。

【设计意图】学生很顺利的通过之前总结的方法，画出了两倍的弧，但是在此过程中，又出现了新的方法，正好是老师需要帮助学生分析的一个点，也是设计两倍弧的意图。

环节三：课堂小结

1、通过本节课的学习，你对于圆的基本性质是否已经完全掌握。

2、你能对这些知识之间的联系做出图示吗？

【设计意图】

通過简单的思维导图，学生把本章中部分关于圆的基本性质的零散知识点整合起来，形成一个完整的知识框架，使头脑中的知识图谱清晰可见。学生在小结的过程中运用思维导图可以针对自己存在的问题，在复习的阶段进行重点突破，也可借此激发学生对后续知识的探索欲望，从而提升学生的思维能力和深度学习的能力。

四、总结反思

教育家苏霍姆林斯基曾告诫我们：“希望你们要警惕，在课堂上不要总是教师在讲，

这种做法不好……要让学生通过自己的思考去理解知识，才能成为自己的知识，才能真正掌握知识，为我所用。”

数学复习课不是原有知识的重复，而是让学生把各个部分知识汇集成完整的知识结构，不能只反复练习几个经典题目，而是要改变学生的学习方法，形成整体的数学逻辑，促进数学学习的能力。这种思维模式的转变，能够促进学生的深度学习，掌握知识更深层次的的本质属性，从而达到举一反三的目的。

在教学设计中，教师要有全盘计划，熟读课标，了解教材，掌握学情，要把实现目标与内容有机统一，突出知识之间的联系，注重问题的变式总结，以达到数学思想方法提升和数学学习能力培养的目的。

教学中不仅要立足于把已学的知识弄懂弄通，把基础打稳打实，更应让学生形成良好的认知结构和知识体系，把解决问题的能力应用到实际生活中，全面提升学生的数学素养。而且还要考虑到如果评价开放性课堂和探究性学习的知识目标完成程度;如何体现在学习过程中的知识建构能力和情感态度与价值观形成能力;如何定义在过程中展现的未来可持续学习潜能的指数等问题。

参考文献：

[1]孙月梅.基于案例分析的初中数学复习课问题研究[D].北京：首都师范大学，2013：5.

[2]王佳.初中数学复习课教学的探索与思考[J].数学学习与研究，2013，（22）：12.

[3]徐骏.“让”为初三数学复习课添彩[J].教育实践与研究（B），2012，（10）：35.

[4]叶立军，徐莉.初中数学复习课教学存在的偏差及其应对策略[J].教学与管理，2013，（5）

[5]朱永灿，韩国荣.新课程下初中数学中考复习教学模式的构建与实践研究[J].世纪之星创新教育论坛，2015，（7）

[6]徐月霞.浅谈提升初中数学复习效益的有效形式[J].中学数学，2014，（5）.