基于强化学习的鱼群自组织行为模拟*

杨慧慧，黄万荣，敖富江

(1. 大连海洋大学 水产与生命学院， 辽宁 大连 116023； 2. 军事科学院， 北京 海淀 100071)

自组织行为广泛存在于自然界中，一个典型的案例就是鱼群。鱼群中的每个个体不仅会主动地相互靠近，还能协同一致地调整自己的行为，以达到群体效果。鱼群的自组织特性有助于提升个体的游动效率、生存和繁衍概率。相对地，目前大部分人造群体系统还只能依靠机械的程控方式完成其功能。如果人造群体可以模仿鱼群的组织方式，将获得更为智能、可观的效能。因此，研究鱼群自组织行为有助于探索自组织行为的内在机理，对实现群体智能有重要的理论意义和应用价值。

Reynolds[1]首次通过计算机程序模拟了鱼群、鸟群等生物群体的自组织行为，并提出了博德模型(Boids model)，即每个智能体基于局部的观察信息，按照避碰、同向、聚集3条规则计算其运动速度，群体便能实现类似生物群体的自组织运动。在博德模型的基础上，多个模型陆续被提出，或优化了原有规则的计算方式，或增加了新的规则。上述模型均能模拟群体的自组织行为，其特点是都假设群体中的个体能够基于感知信息进行复杂计算。然而，这类假设并未触及自组织行为的本质，鱼、鸟等生物个体不一定能进行如此复杂的规则计算。因此，不同于之前基于规则设计模型的研究方式，本文从学习的角度切入，对自组织行为展开研究，通过鱼群行为的模拟，试图探索自组织行为的生成机理。

1 基本概念和相关工作

1.1 自组织

自组织[2]是指一个系统在时间上由无组织到有序的动态过程。自然界广泛存在自组织过程。小鸟成群结队地飞行，以减少风阻、节省能耗；在海洋中，许多鱼经常聚在一起行动，可以比一条鱼更快发现敌人并巧妙地避开；蚂蚁无须复杂的信息交流，可以通过合作高效地完成觅食、搬运等任务；在微观世界，免疫细胞协同合作，攻击侵入生物体的病毒和异物。这些自组织过程是自发产生的，没有外部控制和干预，甚至没有内部集中控制，可使系统更好地适应环境。生物群体自组织行为的一个重要特征是涌现[3]。涌现是指群体中的个体遵循简单的规则(如模仿)，通过自组织就能展现出整体大于部分之和的特性。群体智能[4]的一个研究方向正是通过研究涌现机理而模拟自然界生物群体实现自组织行为。关于自组织行为模拟的研究可以追溯到20世纪80年代。Reynolds[1]提出了博德模型，基于避碰、同向和聚集3条规则成功模拟了鸟群的飞行和避障行为。博德模型也被成功应用于《蝙蝠侠归来》《指环王》等科幻电影的后期制作中，用于模拟蝙蝠群、战士群特效。根据博德模型，Spector等[5]提出了Swarm模型，进一步描述了相邻个体之间的相互作用；Kwong等[6]对Swarm模型进行了仿真，获得了聚集、绕“8”字形等行为特征。Vicsek等[7]根据对磁铁特性的观察，建立了Vicsek模型，假设所有个体速率相同，个体的运动方向取决于它周围个体的运动方向的平均值。Vicsek模型与博德模型类似，都是基于规则的模拟方法。除了在仿真环境中研究之外，Seyfried等[8]用数以千计的微小机器人组成集群，能够像蚁群一样执行一些特定任务，在生产线完成装配任务。Ampatzis等[9]构建一组能够自主组装的机器人，能完成协同搬运、攀爬小山、穿过崎岖地带等复杂任务。Rubenstein等[10]设计了一组微小机器人——Kilobot，1024个功能简单的机器人通过3条简单规则(贴边运动、梯度队形、定位)，通过完全的分布式控制，能够自发形成比较复杂的宏观图形。Kilobot研究成果于2014年发表在《Science》杂志并被评为年度十大科学进展。上述研究工作在不同方面展现了群体自组织的特性，但是都需要通过人为设定若干规则，使得个体在规则的作用下展现出一定的自组织特性。

1.2 赫布迹

赫布迹来源于一个认知生理学理论——赫布定律[11](Hebb′s rule)。加拿大心理学家唐纳德·赫布于1949年提出了赫布定律，描述了突触可塑性的基本原理，即突触前神经元向突触后神经元的持续重复的刺激可以导致突触传递效能的增加。突触可塑性是生物大脑长期学习的重要原因之一。因此，在进化算法中出现了基于突触可塑性设计的塑性神经网络，但是由于技术发展的局限，塑性神经网络不能与成熟的深度学习技术结合。最大的问题在于无法使用深度学习常用的梯度下降方法完成塑性神经网络的大规模反向传播训练。实现塑性神经网络的学习训练，将为神经网络获得像人类一样的持续学习能力提供一种可能性。Miconi等[12]提出了一种可以大规模训练的塑性神经网络。经典的神经网络模型，通常用权值连接对两个神经元之间的关联程度进行量化。这种连接的权值会随着神经网络的训练与反向传播过程不断更新。但是一旦神经网络模型训练完毕，它的权值就不会再发生变化，模型的结构与功能会相应地固化下来。Miconi等设计的塑性神经网络在固定权值连接的基础上，增加了一类权值可变的连接，这类连接的权值称为赫布迹(Hebbian trace)。赫布迹会随着两个神经元的活动而发生变化，即使是在神经网络模型的应用阶段，这种特性也会保持。因此，赫布迹的作用是记忆输入神经元和输出神经元的活动轨迹，从而可以更快地强化巩固新的输入特征，学习到更好的模型。基于这种记忆的作用，塑性神经网络被证明可以应用在模式恢复[13]、小样本学习[12]、自然语言处理[14]等问题中。

1.3 强化学习

强化学习是通过智能体与环境的不断交互，逐渐修正智能体行为策略的一种学习方式。智能体获取环境当前的状态，根据行为策略产生动作决策，作用于环境使其状态发生变化。环境会根据状态变化的“方向”，对该动作决策进行评估，返回一个奖励值。奖励值为正说明该决策产生了有利的结果，奖励值为负则说明该决策产生了不利的影响。智能体根据奖励值修正自己的行为策略，尽可能使动作决策产生有利影响，获得更多累积奖励值。强化学习在机器人、无人驾驶、游戏、自然语言处理、金融、电商等领域有着广泛应用。

强化学习的研究与理论发展有2个重要的方向：多智能体强化学习和深度强化学习。多智能体强化学习研究面临信用分配、搜索空间维度爆炸等挑战。早期研究将多个智能体作为一个整体系统进行学习，然而集中式的方式学习不利于群体规模的扩展。之后，随着博弈论的发展，分布式的多智能体强化学习开始显著发展。近年来，伴随着深度学习引发的人工智能热潮，强化学习与深度学习相结合，出现了深度强化学习技术。深度强化学习结合了深度学习强大的拟合能力和强化学习的交互特性，取得了很多成果。DeepMind基于深度强化学习研发的AlphaGo[15]成为第一个击败人类职业围棋选手和围棋世界冠军的人工智能机器人。Tampuu等[16]将深度强化学习算法深度Q网络(Deep Q-Network, DQN)应用到多智能体游戏环境中，在完全协作环境、完全竞争环境以及非完全协作/竞争环境中学习游戏策略。Lowe等[17]将深度确定性策略梯度(Deep Deterministic Policy Gradient, DDPG)算法扩展到多智能体环境中，提出了多智能体DDPG(Multi-Agent DDPG, MADDPG)算法，并通过共享全局信息训练评价网络，解决环境模型不平稳问题。

2 模型设计

为了实现基于强化学习对鱼群自组织行为进行模拟，首先需要构建环境模型和智能体(鱼)模型。

2.1 环境模型

考虑n条鱼组成的鱼群，用F={f1，f2,…,fn}表示。鱼群在一个二维、封闭、网格化的环境中运动，环境大小为M×M，如图1所示。构建运动世界的坐标系，设最左上角的网格为原点O(0，0)，向右为x轴正方向，向下为y轴正方向。因此，网格A坐标为(M-1，0)，网格B坐标为(0，M-1)。鱼fi的坐标表示为pi(xi，yi)。鱼群运动的环境周围被障碍物包围，环境内部也随机分布着障碍物。用二维矩阵Env表示鱼群运动的环境。Env的元素有1和0两种取值可能：1表示障碍物网格，鱼无法运动到该网格；0表示自由网格，鱼可以运动到该网格。在一些应用场景中，环境中可能存在一个奖励位置(如图1网格中有食物)，坐标为prew(xrew，yrew)。

图1 环境模型Fig.1 Model of the environment

2.2 智能体模型

智能体模型涉及感知、运动和决策3个方面。

2.2.1 感知模型

感知能力描述了鱼能从环境世界获取哪些信息。在自然界，鱼通过鱼眼感知环境，鱼眼的感知和成像功能具有2个特点。首先，鱼眼视野十分广阔，不用转身就能看见前后和上面的物体，例如淡水鲑在垂直面上的视野为150°，水平面上的视野为160°～170°，而人眼分别为134°和154°。鱼在游动过程中，鱼头可灵活变向，且鱼两边都有眼睛，极大地增加观察范围，几乎是全向观察。因此，可以设置每条鱼能感知到以其当前位置为中心、S×S大小的网格状态，如图1中红色网格所示。其次，环境中物体在鱼眼中的成像大小感觉和视角(从物体两端引出的光线在眼光心处所成的夹角)成正比。鱼观察环境中其他鱼时，视角受多种因素的影响，包括其他鱼的大小、位置和方向等。因此，在鱼的大小相同的条件下，可以认为每条鱼能感知到其他鱼的位置和方向。图2展示了鱼感知其他个体的典型情况。基于视角区间，一条鱼可以判断与其他鱼的间隔距离。按照网格可以将距离判断分为3类情况：①视角大于30°时，距离为1；②视角在15°～30°时，距离为2；③视角小于15°时，距离大于2。分析发现，鱼眼这种对距离的度量与切比雪夫距离(Chebyshev distance)度量一致，即：

(1)

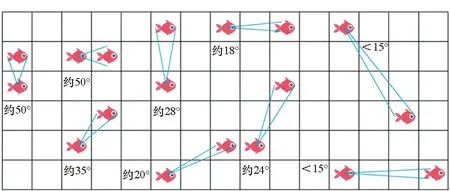
图2 鱼感知其他个体的典型情况Fig.2 Typical situations on perceiving other individuals

2.2.2 运动模型

假设每条鱼具有一阶运动学特性，即通过控制鱼的速度更新鱼的位置。为简单起见，假设鱼游动的速率恒定，为1格/时间步(网格距离基于切比雪夫距离进行度量)。因此，只需要控制鱼的游动方向即可确定鱼的运动过程。需要说明的是，如果鱼试图游动到障碍物网格，则鱼的位置和朝向保持不变，同时设置鱼与障碍物发生碰撞的标志位为True。

2.2.3 决策模型

每一个时间步，智能体需要给出一个动作决策，输入环境以驱动智能体运动。根据智能体的运动模型，鱼需要决策其游动方向。假设鱼可以选择上、下、左、右4个方向中的一个作为该时间步的游动方向。每条鱼的决策策略由一个神经网络拟合，关于神经网络的结构及训练方法将在第3节详细介绍。

2.3 奖励机制

除了构建环境模型和智能体模型之外，还需要对奖励机制进行建模。针对鱼群行为模拟问题，根据智能体与环境的具体交互状态，奖励有4个来源：

1)智能体是否与障碍物发生碰撞。如果智能体与障碍物发生碰撞，奖励为-1；否则，奖励为0。用rcol表示这部分奖励，其计算方式如式(2)所示，其中β1为可调参数，collided是判断智能体是否与障碍物发生碰撞的标志位。

(2)

2)鱼群行为是否符合自组织特性。鱼群行为的特性考虑距离和朝向2类性质。在距离方面，为了使群体展现聚集的特点的同时不会频繁发生个体间碰撞，设置期望距离d。如果个体间的距离恰好等于d，则奖励值最大；如果个体间的距离大于或小于d，则奖励值相应减小。图3(a)给出了基于距离因素衡量奖励值的示意图。在朝向方面，为了使群体展现同向的特点，应使个体的朝向尽量趋同。如图3(b)所示，oi、oj1和oj2分别为智能体i、j1和j2的朝向，如果朝向一致，奖励值越大；如果朝向差异变大，奖励值减小。因此，可以用余弦函数计算基于朝向因素衡量的奖励值。综合距离、朝向2个因素，与鱼群行为相关的奖励rbeh可通过式(3)进行计算，其中β2和β3为可调参数。需要注意的是，式(3)是以智能体i为中心个体计算的奖励值，根据具体任务可以类似地计算以其他智能体为中心的奖励值。

(3)

(a) 距离因素(a) Distance facto (b) 朝向因素(b) Orientation facto图3 考虑距离和朝向因素的奖励值设计Fig.3 Reward value design considering distance and orientation factors

3)在要求群体到达目标位置的场景中，通过智能体与目标位置的距离刻画奖励值。如果智能体距离目标位置越近，奖励值越大；反之，奖励值越小。与目标位置相关的奖励值robj计算方式如式(4)所示，其中β4为可调参数。

(4)

4)为了缓解奖励稀疏可能导致的学习过慢的问题，可以设置提前终止状态并反馈相应的奖励值。提前终止是由于鱼群状态与学习目标差异很大，因此需要返回较大的负奖励值，并进入下一个学习过程。用rter表示与提前终止相关的奖励值，计算方式如式(5)所示，其中β5为可调参数，terminal是判断某次学习过程是否提前终止的标志位。

(5)

因此，某一时间步，环境向智能体i反馈的奖励值是上述4部分之和：

r=rcol+robj+rbeh+rter

(6)

3 算法

为了以学习的方式获得鱼的行为策略，基于赫布迹和A2C框架[18](一种行动者-评价者框架)实现了一种多智能体深度强化学习算法。算法框架如图4所示，主要包括鱼群模拟环境和鱼群游动策略两部分。鱼群模拟环境建模已在第2节给出，鱼群游动策略则由n个个体独立的策略组合而成。每条鱼私有一个带赫布迹的神经网络，因此，本文提出一种分布式强化学习算法。在学习阶段，由于所有智能体是同构的，可借鉴网络冻结[19]的思想，先训练f1的策略网络而固定其他鱼的策略，然后将学好的f1的策略网络参数复制给其他智能体(见图4空心箭头)，再进行下一轮f1策略网络训练。

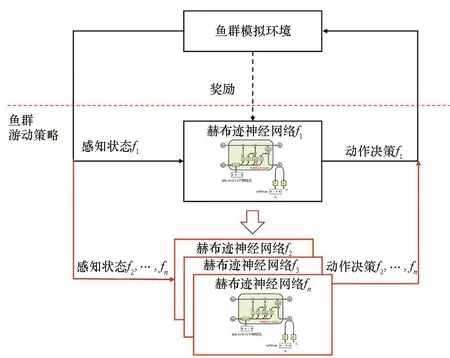
图4 策略学习框架Fig.4 Framework of the strategy learning

3.1 鱼群学习算法

整个鱼群行为的学习过程如算法1所示。由于网络本身具有记忆特性，没有使用记忆池与经验回放等技术。假设学习过程一共持续Nmax个回合(第14行)。每个回合中，鱼群会与环境进行若干时间步的交互。在时间步T，所有鱼获取当前时间步的感知状态st，由策略拟合网络产生动作决策at和状态评价Vt。动作决策施加在环境之后，环境向智能体反馈一个奖励值rt，同时环境状态演变为st+1。如果满足回合终止条件，即T大于Tmax或标志位terminal为True，环境状态复位，进入下一回合的交互过程(第9行)。否则，terminal为False，继续该回合下一个时间步的交互(第8行)。

根据f1与环境在一个回合中的交互数据(s0,a0,r0,s1,a1,r1,…,sT)可以计算损失函数J的值(第10行)，具体计算方式如式(7)～(10)所示：

(7)

(8)

Ri=r0+γr1+γ2r2+…+γTrT

(9)

(10)

其中：式(8)的π(ai|si;θa)表示策略网络拟合的动作决策函数，θa表示与动作决策相关的网络参数；式(9)中的γ表示奖励折扣因子；式(8)和式(10)中的V(si;θv)表示策略网络拟合的状态评估函数，θv表示与状态评估相关的网络参数。因此，θa与θv共享一部分参数。f1根据损失函数J值进行梯度下降，通过反向传播更新策略学习网络参数。其他所有鱼则会在回合结束时复制f1学习到的策略(第12行)。显然，根据算法1学习到的鱼群行为，所有鱼的行为特点是趋同的。

算法1 鱼群行为策略学习

3.2 策略网络结构

算法中，每个智能体的策略用一个带赫布迹的神经网络进行拟合，所有智能体的策略网络结构相同，其网络结构如图5所示。

图5 策略学习网络结构Fig.5 Structure of the strategy learning network

策略网络有3(n-1)+S2+1个输入神经元。第一部分的3(n-1)个神经元记录了其他智能体的状态，包括位置坐标和朝向。中间一项S2个输入神经元是智能体i对环境状态的感知，记录了以智能体i为中心、附近S×S个网格的状态。最后一个神经元输入的是时间。整个策略学习网络的核心结构是一个长短时记忆(Long Short-Term Memory，LSTM)单元。LSTM是一类具有长期记忆和短期记忆的结构。如图5所示，在LSTM单元的输入门结构中增加了赫布迹项，用于强化LSTM单元的记忆特性。LSTM单元t时刻的内部状态ct的计算过程变为：

ct=ft⊙ct-1+it⊙gt

(11)

ft=σ(Wfh·ht-1+bfh+Wfx·xt+bfx)

(12)

it=σ(Wih·ht-1+bih+Wix·xt+bix)

(13)

gt=tanh[(Wgh+α·Hebb)·ht-1+Wgx·xt+bgx]

(14)

(15)

其中，η是控制记忆强度的系数。基于LSTM单元的输出，策略学习网络的输出分为2个部分。一部分是智能体在时间步T的动作决策at，它以独热编码的方式表示智能体的每一种可选动作。另一部分输出是状态评价Vt，它以一个实数值对输入状态的“好坏”进行评价。Vt值越大表示认为当前状态越“好”，越有利于智能体的策略学习。虽然动作决策和状态评价共享了一部分网络单元，但整个策略学习网络的训练方法与Minh等[19]提出的方法可以保持一致。

4 实验结果

为了评估第3节提出的网络结构与算法是否可用于学习到合理的鱼群行为，进行了一些实验并给出结果。首先在3类群体场景中测试了本文方法的学习效果，分别是领航跟随场景、自主漫游场景和群体导航场景。然后对比了本文方法与基于博德规则计算模拟的方法。

4.1 领航跟随场景

在领航跟随场景中，群体有一个领航者个体带领其他个体运动，其余个体则作为跟随者跟随领航者一起运动。通过领航与跟随的形式，鱼群便能展现整体运动特性。设有一个3条鱼组成的鱼群(n=3)，不失一般性，假设f3是领航者，f1和f2是跟随者。f3由外部控制器作用，在环境中作周期环绕运动，其路径如图6中红线所示。f1与f2的行为策略由网络拟合并通过算法1学习训练获得。针对领航跟随场景实验的具体参数设置为：环境大小M=15，感知范围S=5；奖励机制的可调参数β1=0.1，β2=0，β3=0，β4=0，β5=10；Tmax=250，提前终止条件为跟随者与领航者的距离超过2。图6给出了鱼群在一次典型测试回合中T=7、T=15、T=91时运动状态，可以发现，本文学习算法学到的策略能让f1和f2跟随f3环绕运动。

图6 领航跟随场景的学习结果Fig.6 Results of learning in the leader-follower scenario

4.2 自主漫游场景

自主漫游场景的设置如图7所示，与领航跟随场景相比，鱼群中没有领航者个体，所有个体需要在环境中以整体的形式随机漫游。如果环境中存在障碍物，鱼群需要避开障碍物。设有一个3条鱼组成的鱼群(n=3)，f1、f2与f3的行为策略均由网络拟合并学习训练获得。针对自主漫游场景实验的具体参数设置为：环境大小M=11，感知范围S=5；奖励机制的可调参数β1=1，β2=1，β3=0，β4=0，β5=0；Tmax=250，无提前终止条件。图7展示了一次典型测试过程鱼群运动状态的变化情况。在T=76时，所有个体朝着上方运动，且个体之间距离为1。在T=130时，所有个体朝着下方运动，且个体之间距离为1。经数据统计，在250个时间步内，鱼群始终聚集在一起，互相碰撞0次，碰到障碍物1次，说明鱼群学会了博德规则中的“聚集”规则，同时还可避开环境中的障碍物。

图7 自主漫游场景的学习结果Fig.7 Results of learning in the autonomous wandering scenario

4.3 群体导航场景

图8 群体导航场景的学习结果Fig.8 Results of learning in the group navigation scenario

在群体导航场景中，鱼群中所有个体需要朝着给定目标协同地运动。如果环境中存在障碍物，鱼群需要避开障碍物。设有一个3条鱼组成的鱼群(n=3)，f1、f2与f3的行为策略均由网络拟合并学习训练获得。针对群体导航场景实验的具体参数设置为：环境大小M=19，感知范围S=5，奖励位置为prew(5，13)；奖励机制的可调参数β1=1，β2=1，β3=2，β4=10，β5=0；Tmax=50，无提前终止条件。图8展示了一次典型测试过程鱼群运动状态的变化情况。初始时刻，鱼群的状态如图8中T=0时所示鱼群。模拟开始后，鱼群一直朝右侧方向游动，直至T=5时，即将碰到环境中的障碍物。鱼群改变游动方向，朝右上侧游动绕过障碍物并接近奖励位置，到达T=11的状态。当T=16时，鱼群到达奖励位置。之后鱼群将围绕奖励位置在水平方向往复运动。经数据统计，碰到障碍物0次。实验结果表明鱼群学会协调地绕过障碍物，到达奖励位置。鱼群游动过程展现出聚集、同向特性。

4.4 对比实验结果

为了说明赫布迹的引入对于学习过程的影响，图9给出了群体导航学习训练过程中，有赫布迹项和无赫布迹项2种条件下的群体奖励值的变化曲线。可以发现，有赫布迹项时，群体在约80 000 个学习回合之后的学习过程相比无赫布迹项时明显加快，使得最终的奖励值更优，即群体所学到的行为更加符合自组织行为的特点，也表明赫布迹项的记忆特性对于群体学习过程起到了正面促进作用。

图9 有赫布迹项和无赫布迹项条件下的学习结果Fig.9 Results of learning with and without the Hebbian trace

基于群体导航场景的实验结果，通过改变奖励机制的可调参数、改变鱼群个体数量、改变奖励位置进一步测试学习算法的效果，获得统计结果如表1～2所示。

表1 鱼群模拟对比实验参数设置

表2 鱼群行为特点对比

为了对比基于学习方法模拟的鱼群行为与基于博德规则模拟的鱼群[20]行为特点，设计了2个量化指标进行衡量：一个是位置偏差m1，对应博德模型中的“聚集”和“避碰”规则；另一个是朝向偏差m2，对应博德模型中的“同向”规则。m1和m2的具体计算方式如式(16)～(17)所示。

(16)

(17)

通过表2的数据对比分析可知，在位置偏差度量上，基于学习方法模拟的鱼群行为特点与基于博德规则模拟的鱼群类似。而在朝向偏差度量方面，当可调参数β4显著减小时，例如实验设置A1对比A，由于与目标导航相关的奖励值权重显著减小，目标位置对于每个个体的方向导引作用减弱，使得鱼群在个体相互作用下表现出更好的方向趋同性。进一步，实验设置A2对比A1，当可调参数β3增大时，由于与朝向相关的奖励值权重增加，模拟的鱼群展现更好的方向趋同性。相反，当β3减小时，例如实验设置A3对比A，与朝向相关的奖励值权重减小，模拟的鱼群方向趋同性相应变差。因此，对比实验结果进一步证明了学习方法的有效性。

5 结论

为了从学习的角度切入实现鱼群自组织行为模拟，首先构建了鱼群模拟框架，包括鱼群运动环境模型，智能体的感知、运动和决策模型和奖励机制。接着，基于赫布迹和行动者-评价者框架提出了一种多智能体强化学习方法。在学习训练阶段，该方法利用网络冻结的思想实现了分布式学习，有助于群体规模扩展，并利用赫布迹优化了策略学习过程。仿真结果表明，该方法在领航跟随、自主漫游、群体导航等场景均成功学到了鱼群自组织行为。进一步数据分析发现，基于学习方法模拟的鱼群与基于博德规则计算模拟的鱼群在行为特性上表现出一定相似性。在后续工作中，以学习结果为基础，将进一步基于直觉物理、随机选择计算等类人智能因素对鱼群自组织行为展开研究。