次级通道估计误差对Fx-Newton算法的影响*

张 能，何 琳，李 彦，王迎春

(1. 海军工程大学 振动与噪声研究所， 湖北 武汉 430033；2. 海军工程大学 船舶振动噪声重点实验室， 湖北 武汉 430033)

对于船舶机械低频振动线谱，通常采用主被动隔振的方法加以控制，而自适应控制算法在执行过程中通常需要对由作动器输出到误差信号的次级通道进行模型估计或辨识，在此过程中不可避免会引入误差，因此开展次级通道估计误差对自适应控制算法的影响研究具有重要意义。

文献[1]通过分析传递函数的极点位置和根轨迹，研究了次级通道相位估计误差对最小均方滤波(the Filtered-x Least Mean Square, FxLMS)算法收敛速度和稳定性的影响，结果表明次级通道相位估计误差小于90°时能收敛，当相位估计误差小于45°时，相位误差对收敛时间影响较小。文献[2-3]针对噪声主动控制系统，采用随机分析的方法，研究了次级通道估计误差对FxLMS算法性能的影响，发现当次级通道真实模型与估计模型负相关时，控制系统不稳定。王雷针对次级通道估计相位误差对FxLMS算法的收敛性开展了研究，通过仿真发现相位延迟越大，系统收敛速度越慢，稳定性越差[4]。Hansen等忽略真实的次级通道传递函数(假设该传递函数幅值为1，相位为0°)，理论推导了步长因子的取值范围，分析了次级通道估计误差对频域FxLMS算法稳定性的影响[5]。

FxLMS算法的收敛速度受制于滤波参考信号自相关矩阵的特征值分布，实时性较差，而Fx-Newton算法具有收敛速度快、对矩阵特征值分散度不敏感的优点，文献[6-8]将Fx-Newton算法应用于船舶机械主被动隔振系统中，有效隔离了振动线谱。然而，在Fx-Newton算法执行过程中需要估计次级通道模型，而针对次级通道估计误差对Fx-Newton算法的影响，未见学者开展相关研究。

本文通过在频域Fx-Newton算法中引入估计误差模型，假设输入信号为正弦信号，基于含次级通道估计误差的Fx-Newton算法迭代公式，通过理论推导，从次级通道估计相位误差和幅值误差两方面来分析Fx-Newton算法的稳定性和收敛性。最后建立两自由度主被动隔振模型，在不同相位误差和幅值误差条件下开展主动控制仿真，以验证理论分析结果。

1 含次级通道估计误差的Fx-Newton算法推导

文献[6-8]推导了Fx-Newton算法的滤波器更新方程，基本的Fx-Newton算法的原理如图1所示。

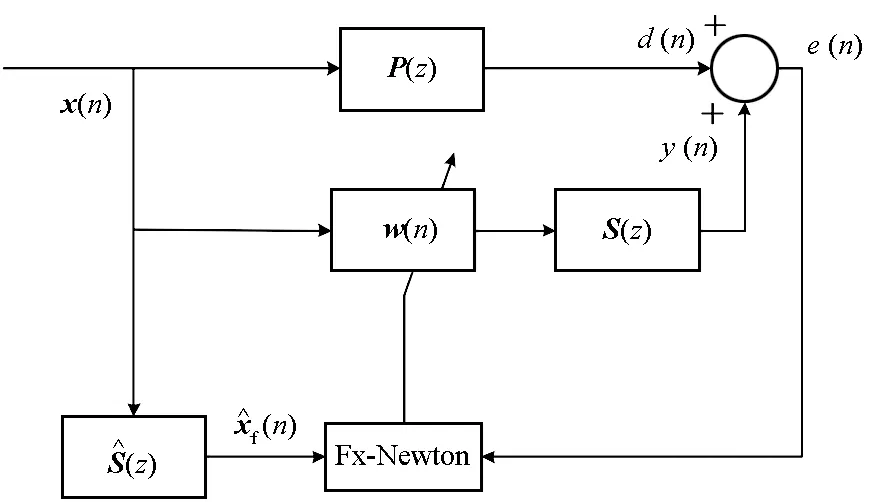
图1 Fx-Newton算法结构框图Fig.1 Block diagram of the Fx-Newton algorithm

Fx-Newton算法中滤波器系数的更新公式表示为

(1)

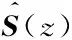
次级通道模型的估计包含于Fx-Newton算法的迭代公式中，在实际工程应用中不可避免地会出现误差，影响着算法的稳定性和收敛性。在主被动隔振系统应用中，通常控制的是振动线谱，这里为了研究方便，考虑输入为某一正弦信号，并且算法在频域执行，次级通道模型估计误差表示为H(z)，则考虑次级通道模型估计误差的自适应前馈控制系统如图2所示。

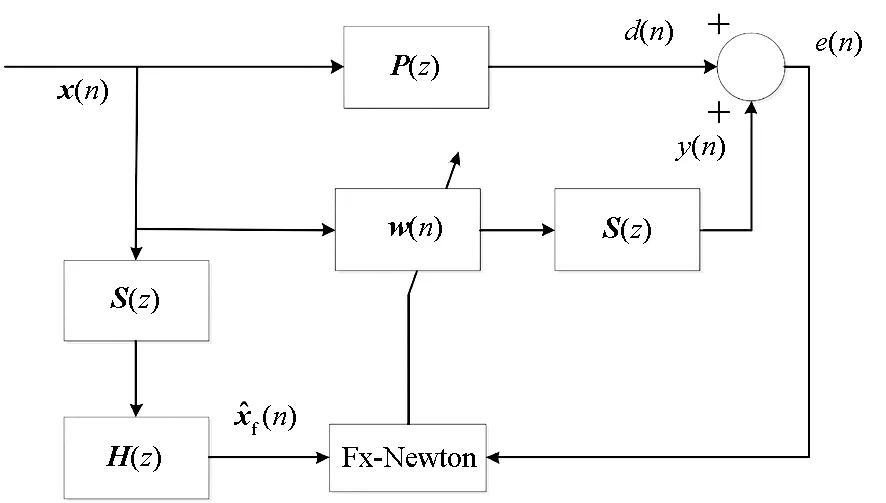
图2 考虑次级通道估计误差的Fx-Newton算法结构框图Fig.2 Block diagram of the Fx-Newton algorithm considering the estimation error of the secondary path model

频域Fx-Newton算法的迭代公式可以表示为

(2)

式中，“*”表示共轭。

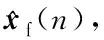
(3)

记次级通道估计误差的相位为φh，则复数h可以表示为

h=|h|ejφh

(4)

其中|h|=1和φh=0°表示次级通道估计不存在幅值误差和相位误差。

由图2可知，误差信号e(n)表示为

e(n)=d(n)+wT(n)xf(n)

(5)

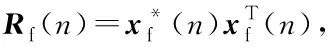
(6)

将式(3)、式(6)代入式(2)中，可得

(7)

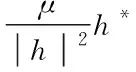
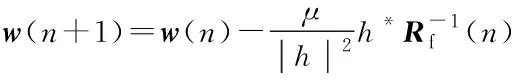
(8)

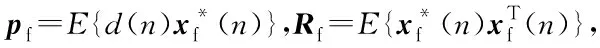
(9)

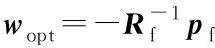
(10)

当n→∞时，v(n)必须收敛到零，Fx-Newton算法才能稳定，则下面的条件必须满足

(11)

将h*=|h|e-jφh代入式(11)中，可得

(12)

将式(12)展开得到

(13)

式(13)化简可得

μ<2|h|cosφh

(14)

其中|h|为次级通道估计误差的幅值，因此，对于次级通道估计存在误差的系统，Fx-Newton算法的稳定性条件为

0<μ<2|h|cosφh

(15)

由式(15)可知，次级通道模型估计误差对Fx-Newton算法的影响可以分为相位误差和幅值误差两部分来讨论。

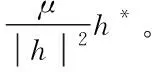
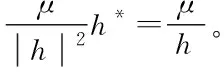
2 两自由度主被动隔振模型与仿真算例

2.1 两自由度主被动隔振模型

下面建立两自由度主被动隔振模型，其结构如图3所示。上层机械设备质量为m1，下层平台质量为m2，上层隔振器刚度和阻尼分别为k1和c1，下层隔振器刚度和阻尼分别为k2和c2，作动器和上层被动隔振器并联，f为激励力，fa为主动控制力。设x1、x2表示机械设备和下层平台的垂向位移，则该系统的运动方程为

(16)

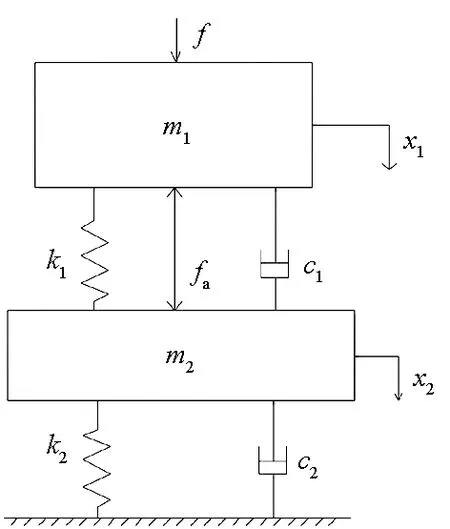
图3 两自由度主被动隔振模型Fig.3 Two degree-of-freedom active-passive vibration isolation model

(17)

化简，消去X1可得

[m1m2s4+(m1c1+m1c2+m2c1)s3+
(m1k1+m1k2+m2k1+c1c2)s2+
(c1k2+c2k1)s+k1k2]X2
=m1s2Fas+(c1s+k1)Fs

(18)

记a=m1m2，b=m1c1+m1c2+m2c1，c=m1k1+m1k2+m2k1+c1c2，d=c1k2+c2k1，e=k1k2，分别令Fs=0、Fas=0，可得下层平台位移X2和激励力Fs、主动控制力Fas之间的传递函数

(19)

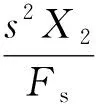
2.2 仿真算例

表1给出了2.1节两自由度主被动隔振模型的参数值。

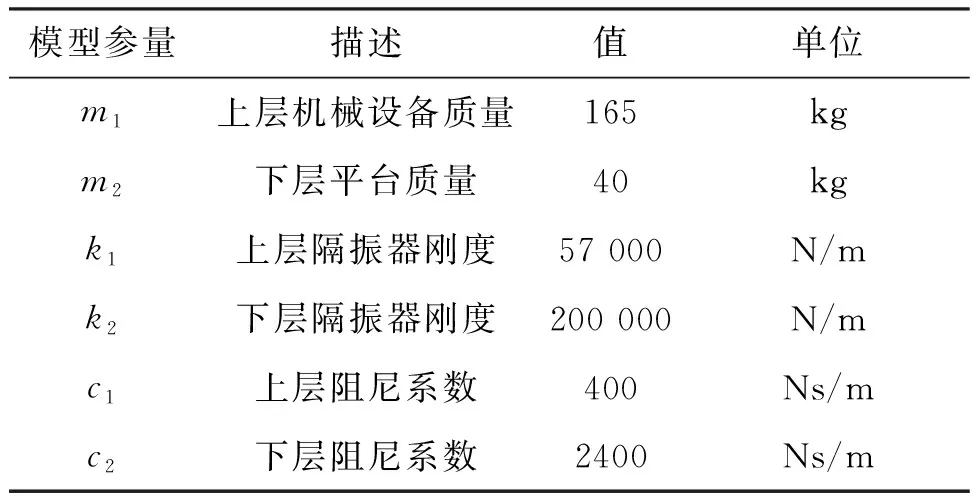
表1 主被动隔振模型参数

根据主被动隔振模型，在Simulink/MATLAB中建立仿真模型如图4所示，其中Fx-Newton算法通过自定义的S函数模块实现，Fx-Newton算法的步长因子为0.000 2，初始时滤波器系数为零矢量，阶数为64。由于Euler求解器具有简单、计算效率高的优点，仿真采用固定时间步长的Euler求解器。仿真时间步长为0.001 s，仿真时间为10 s，在1 s时开启主动控制。

激励力为多频正弦激励，由25 Hz和50 Hz的正弦波与表示外界干扰的高斯白噪声叠加而成，其表达式为

f=6sin(50πt)+10sin(100πt)+n0

(20)

其中，n0表示高斯白噪声，其均值为0，方差为0.01。

3 结果与讨论

3.1 次级通道估计相位误差的影响

考虑次级通道估计不存在幅值误差(|h|=1)，分别在次级通道估计相位误差φh为0°、45°、 90°时，对图4所示主被动隔振模型开展仿真，得到控制后下层平台振动加速度的时间历程曲线和功率收敛曲线分别如图5、图6所示。

由图5可知，随着次级通道估计相位误差从0°增大到45°，下层平台振动加速度收敛速度降低，当相位误差增大到90°时，下层平台振动加速度在控制后直接发散。同时图6也反映出相位误差从0°增大到45°时收敛速度降低，相位误差为90°时功率收敛曲线在控制后直接发散，说明相位误差的存在降低了Fx-Newton算法的稳定性，当相位误差达到90°时，Fx-Newton算法直接发散，与理论分析结果一致。

3.2 次级通道估计幅值误差的影响

考虑次级通道估计没有相位误差(φh=0°)，分别在幅值误差|h|为0.5、1、2时开展主被动隔振系统仿真，得到控制后下层平台振动加速度的时间历程曲线和功率收敛曲线分别如图7、图8所示。

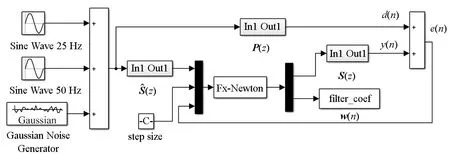
图4 主被动隔振模型Simulink/MATLAB仿真模型Fig.4 Simulation model of the active-passive vibration isolation system in the Simulink/MATLAB

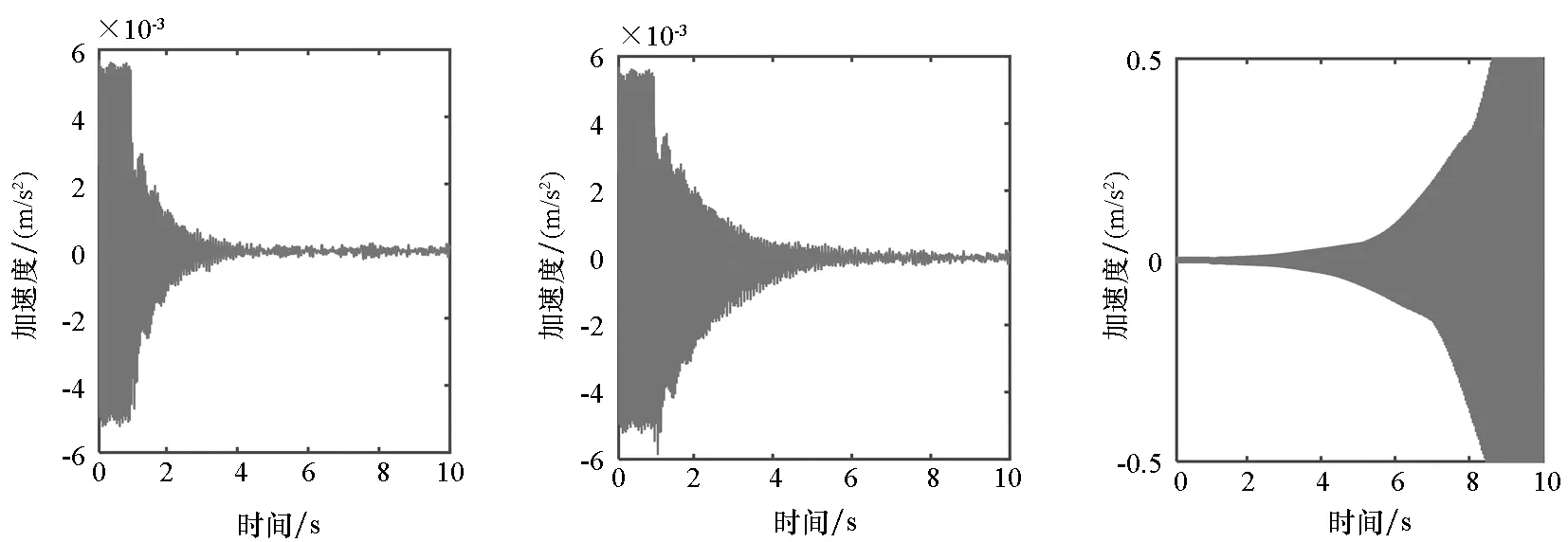
(a) φh=0° (b) φh=45° (c) φh=90°图5 不同相位误差时下层平台振动加速度时间历程曲线Fig.5 Curves of the acceleration of the middle raft under different phase errors

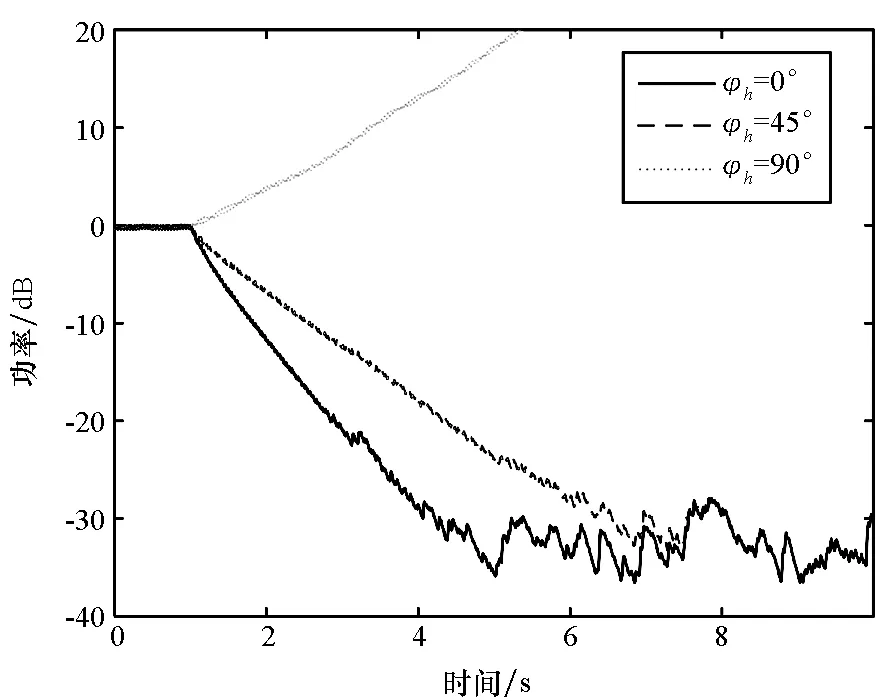
图6 不同相位误差时下层平台振动功率收敛曲线Fig.6 Curves of the vibrational power of the middle raft under different phase errors

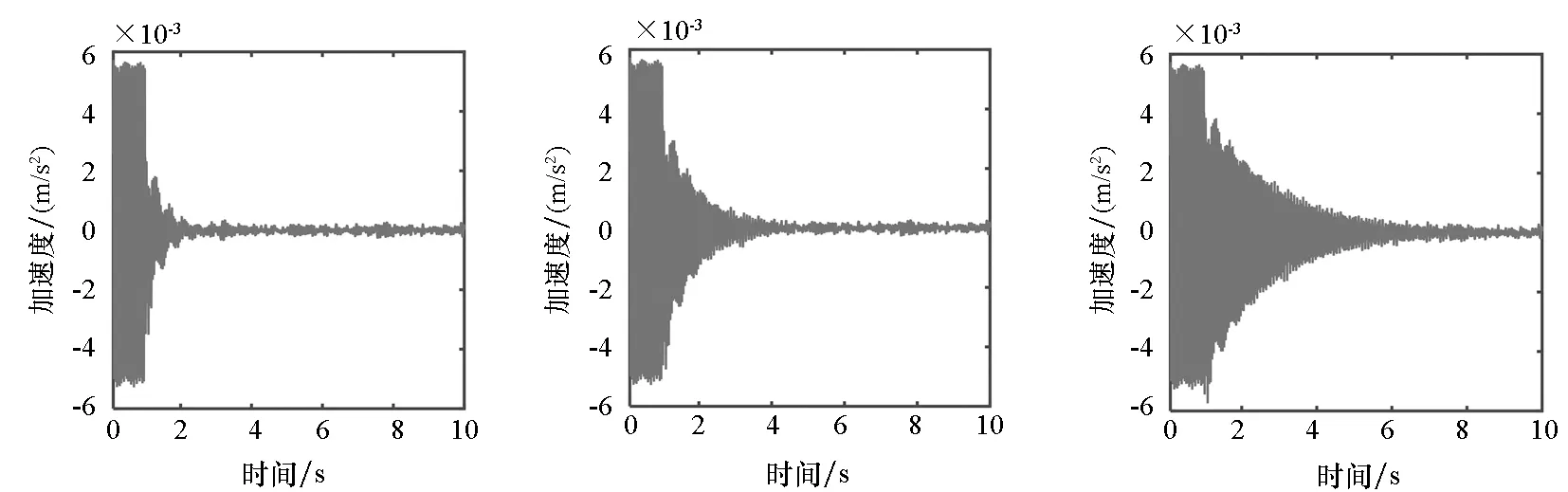
(a) |h|=0.5 (b) |h|=1 (c) |h|=2图7 不同幅值误差时下层平台振动加速度时间历程曲线Fig.7 Curves of the acceleration of the middle raft under different amplitude errors

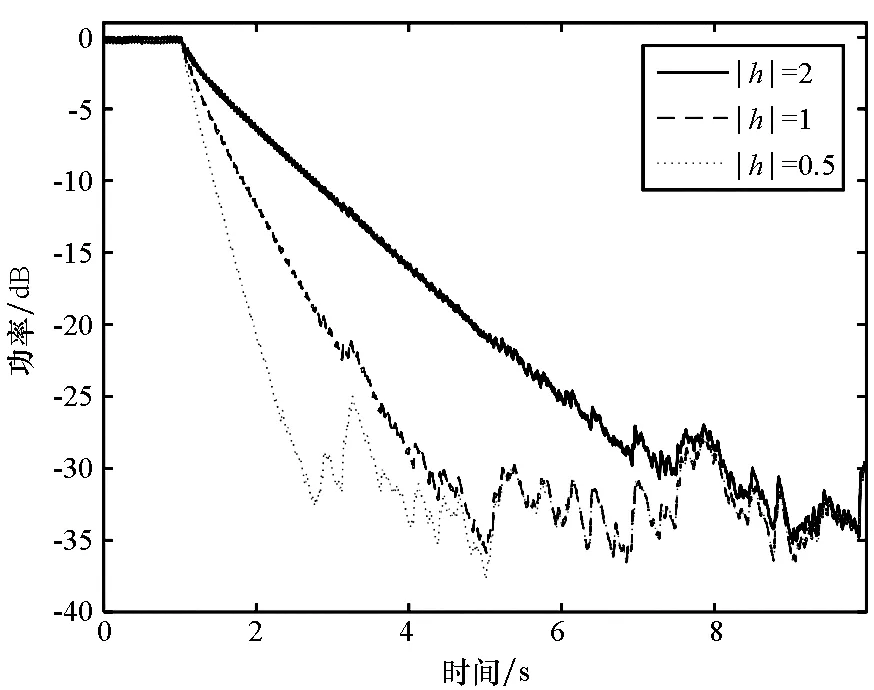
图8 不同幅值误差时下层平台振动功率收敛曲线Fig.8 Curves of the vibrational power of the middle raft under different amplitude errors

由图7、图8可知，当次级通道估计幅值误差|h|=0.5时，下层平台振动加速度收敛速度较不存在幅值误差时(|h|=1)快，Fx-Newton算法能更快收敛到稳态；当次级通道估计幅值误差|h|=2时，下层平台振动加速度收敛速度较不存在幅值误差时慢，Fx-Newton算法收敛速度降低，验证了理论分析的结果。

4 结论

针对次级通道估计存在误差的问题，在正弦输入信号假设条件下，理论推导了含次级通道估计误差的频域Fx-Newton算法迭代公式，阐述了Fx-Newton算法的稳定性条件，并就相位误差和幅值误差对Fx-Newton算法稳定性和收敛性的影响作了理论分析。结果发现：当相位误差大于90°或者小于-90°，Fx-Newton算法会发散；当相位误差在-90°～90°范围内，Fx-Newton算法的稳定性会在一定程度上降低，同时收敛速度也会降低。当幅值误差小于1时，Fx-Newton算法的收敛速度较不存在幅值误差时快；当幅值误差大于1时，Fx-Newton算法的收敛速度较不存在幅值误差时降低。通过对两自由度主被动隔振模型开展仿真研究，验证了理论分析结果。本文的研究结果对提高Fx-Newton算法在工程应用中的稳定性和收敛性具有重要意义。