开口金属腔体对强电磁脉冲的耦合效应*
2020-02-07陈宗胜李志刚
陈宗胜,李志刚
(国防科技大学 脉冲功率激光技术国家重点实验室, 安徽 合肥 230037)
电子设备在各种武器系统中的作用越来越重要,而强电磁脉冲武器的出现对电子设备构成了严重威胁[1-2]。一般来说,电子设备外部通常会加有金属腔体进行保护,但是在实际工作中,为便于散热和传输信号等,金属腔体表面不可避免地留有开口和孔缝,这为电磁脉冲信号进入金属腔体内部提供了有效途径[3-4]。当强电磁脉冲照射在金属腔体表面时,入射波一方面在金属腔体表面形成次级辐射源,持续向腔内辐射电磁能量,另一方面,通过腔体表面的开口直接耦合进入腔体内部,从而在腔体内部叠加形成复杂的电磁分布。当耦合进入腔体内的能量达到一定程度时,将会干扰甚至破坏腔体内电子设备的正常工作。
目前,电磁脉冲武器主要有核电磁脉冲(High-amplitude ElectroMagnetic Pulse, HEMP)和高功率微波(High Power Microwave, HPM)两种辐射类型[5],研究这两种强电磁脉冲耦合进入开口金属腔体内的电磁特性,不论是对于己方电磁脉冲武器的效能评估还是对于敌方电磁脉冲武器的防护都具有重要的意义。当前,关于强电磁脉冲的孔缝耦合效应的探讨,国内外进行了大量的研究工作。王建国等采用时域有限差分(Finite Different Time Domain, FDTD)模拟法计算分析了强电磁脉冲通过孔缝的耦合效应,研究表明屏蔽体内孔缝附近的耦合场强最大[6];鲍永波等分析了电磁脉冲对正方形孔洞和长方形孔洞的耦合效应,研究表明耦合效应会受到极化方向的影响[7]。在前人的基础上,本文进一步研究分析了腔体开口因素对强电磁脉冲破坏效能的影响,利用CST电磁仿真软件建立了强电磁脉冲的孔缝耦合模型,利用该模型,通过考察不同情形下腔体内耦合能量的改变,研究了腔体上孔缝的位置、大小以及长宽比等因素对HEMP和HPM耦合效应的影响。
1 仿真模型
图1为利用CST软件建立的电磁脉冲孔缝耦合模型,电磁脉冲采用平面波激励,传播方向为-z方向,入射波电场和磁场方向分别为+x和-y方向。腔体大小为1000×1000×1000(若无特殊说明,模型中尺寸单位均采用mm),腔体材质设置为完美电导体,腔壁厚度为5,在z=1000、xy平面中心处设置正方形开口,开口大小为200×200,背景设为空气。
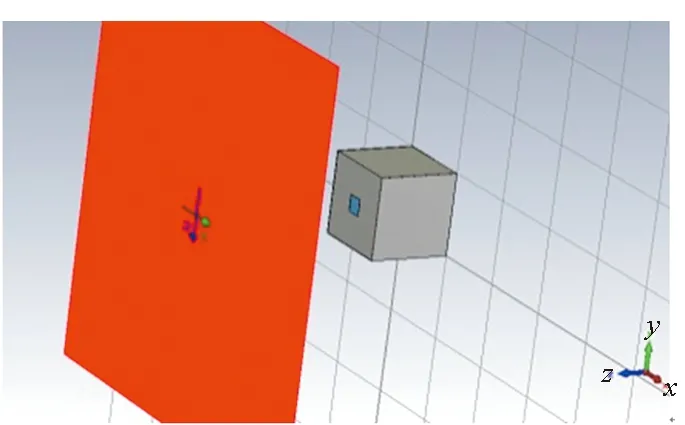
图1 电磁脉冲孔缝耦合模型Fig.1 Coupling model induced by powerful electromagnetic pulse
为了便于后续仿真结果分析,在计算过程中,设置电场强度探针用于记录强电磁脉冲在腔体不同位置处的耦合信号特征。将电场探针分别设置在目标腔体内部中轴线不同位置(yz平面,x=500),如图2所示,分别为Middle probe(500,500,1000)、A0 probe(500,500,900)、B0 probe(500,500,500)、C0 probe(500,500,100)。
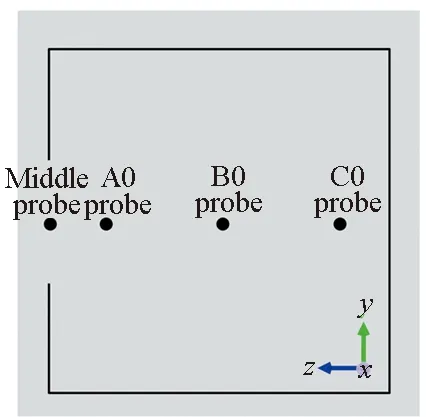
图2 电场强度探针设置示意Fig.2 Schematic diagram of electric field probes inside the cavity
2 强电磁脉冲设置
2.1 HEMP的设置
目前,电磁脉冲弹是典型电磁脉冲武器之一,其辐射的HEMP时域波形可采用双指数函数来表达[8-9],具体为:
E(t)=E0·k·[exp(-αt)-exp(-βt)]
其中,E0为脉冲峰值场强,α、β的值影响波形脉宽、上升时间等参数。
选取文献[8]所述的典型电磁脉冲弹辐射的电磁脉冲作为参考,假设E0=5×105V/m,k=1.214,α=3.5×106,β=1.5×109,波形上升时间为2.645 ns,脉冲宽度为100 ns,峰值功率为1×109W/m2,在100 ns的时间内辐射的总能量密度为1.3×10-3J/cm2。
2.2 HPM的设置
HPM辐射电场通常近似表示[10-11]为:
其中,E0为场强峰值,τ为脉宽,t1为脉冲上升时间和下降时间,f0为载波频率。
选用6 GHz作为HPM的载波频率,根据文献[11]给出的高功率微波武器参数,假设有效功率密度为5×109W/m2,场强峰值E0=2×106V/m,在100 ns的辐射时间内释放的总能量密度为5×10-2J/cm2。
3 结果及分析
3.1 仿真结果与数据处理
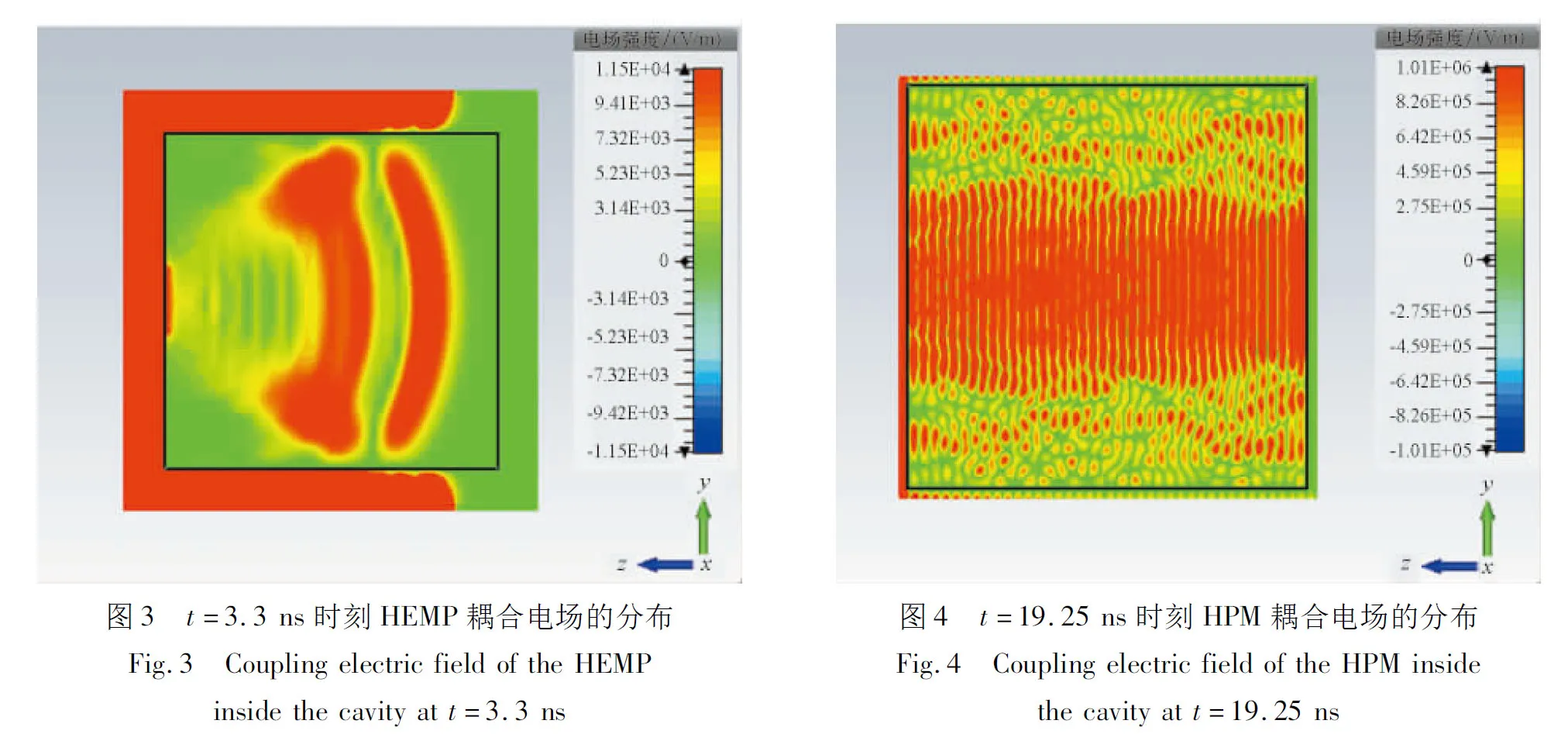
利用前面的模型即可计算得到不同时刻强电磁脉冲耦合进入开口金属腔体内的电磁场。图3和图4分别给出了t=3.3 ns时刻HEMP以及t=19.25 ns时刻HPM在yz(x=500)平面上耦合电场的分布。从图中可以看出,两种强电磁脉冲可通过腔体开口向腔内辐射能量,入射波会在腔内振荡传播,形成独特的空间电磁分布。
通过对所设置的电场探针测得的信号进行提取,可以得到不同位置处耦合信号的时域波形,如图5所示。对于HEMP,Middle probe和A0 probe测得的电场强度峰值较大,B0 probe和C0 probe处电场强度峰值较小,并且均小于入射场强峰值,这说明只有少部分HEMP能量能耦合进入腔体内部。对于HPM,B0 probe和C0 probe处测得的电场强度大于Middle probe和A0 probe处,并且峰值大于入射场强峰值2×106V/m,这一现象与HEMP孔缝耦合效应有所不同。产生这种现象的原因在于:入射HPM频率较高,耦合进入腔体内部受到孔缝的限制较小,同时,耦合过程中进入腔体内部的电磁能量不断叠加积累,从而导致腔体内部分区域的场强峰值会大于入射场强峰值。
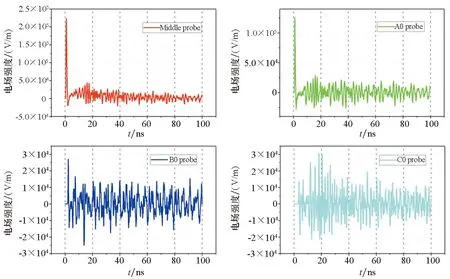
(a) HEMP
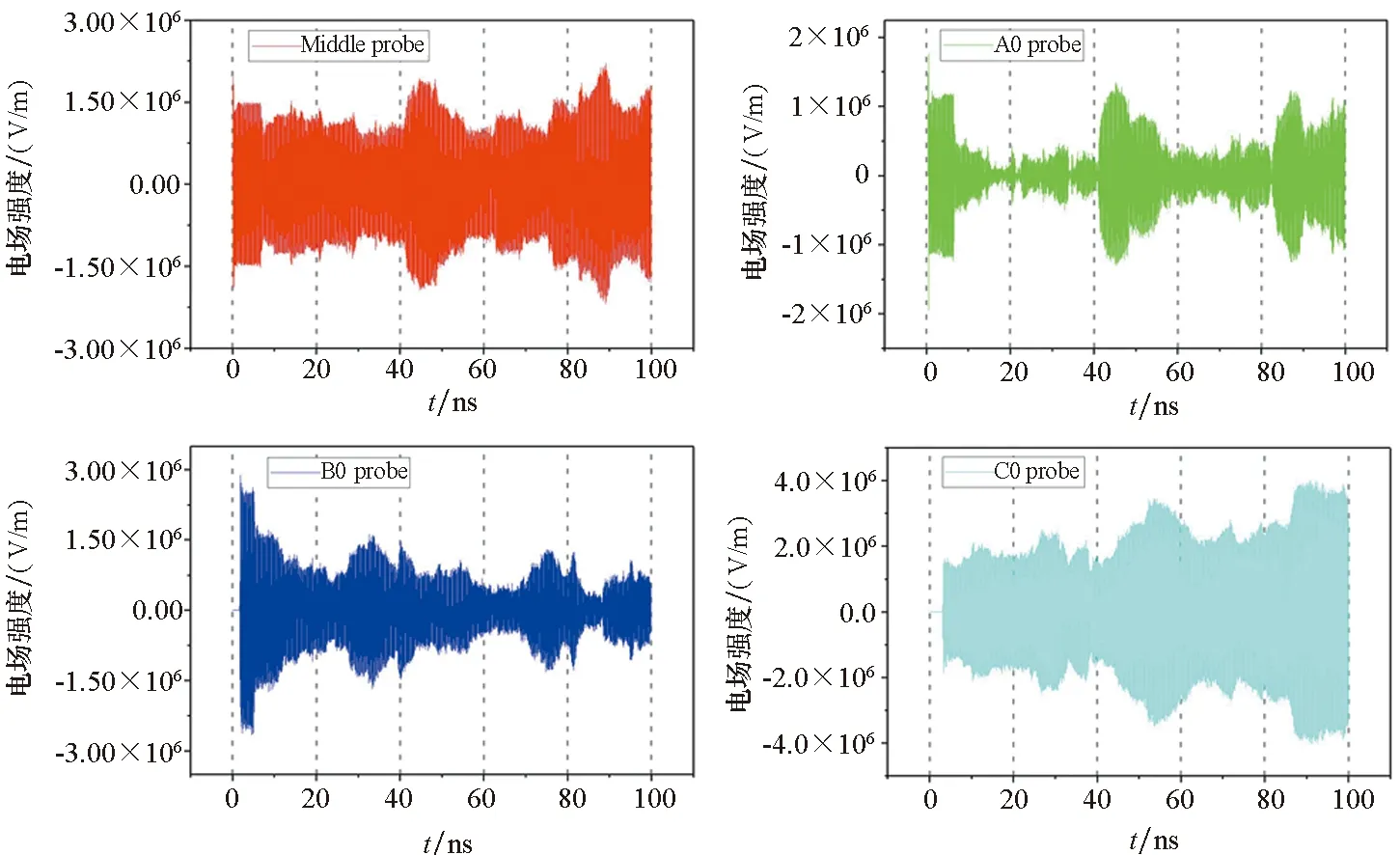
(b) HPM图5 电场强度探针测得的耦合信号Fig.5 Coupled signals measured by the electric field probes
对不同条件下探针测得的电场信号进行处理,得到的功率密度和能量密度值如表1所示。从表中可以看出,HEMP和HPM耦合到腔体内的能量已达多种电子元器件破坏阈值级别[12-14]。若进一步增加辐射功率和辐射时间,则会导致更多的电子元器件被破坏。此外,对比两种强电磁脉冲释放的总能量以及腔体内的耦合能量可以看出,在上述仿真条件下,HPM进入腔体内的耦合效率要明显高于HEMP。
考虑强电磁脉冲进入金属腔体内部的耦合效应还会与腔体开口的大小与分布等因素有关,为此,下面从腔体开口因素展开研究,分析开口位置、大小以及开口长宽比对耦合效应的影响,考察不同情形下耦合能量的改变。
3.2 开口位置对腔内电场的影响
保持激励波的大小和方向不变,开口大小仍设为200×200,分别将开口位置设置在x平面(x=1000,此时开口平面与激励波入射方向平行,与电场方向相垂直)、y平面(y=1000,此时开口平面与激励波入射方向平行,垂直于磁场方向)和z平面(z=1000,此时开口平面与激励波入射方向相垂直),并按照开口位置对相应的电场探针进行调整,其他仿真条件设置不变。
对计算所得的数据进行整理计算,可以得到不同探针处的平均功率密度和总的能量密度值。表2为C0 probe处的数据处理结果。从表中可以看出,不同开口位置下电场探针测得的电场信号值差别较大,这说明腔体开口位置对强电磁脉冲耦合效应具有较大影响。不论是对于HEMP还是HPM,当腔体开口平面与激励波入射方向垂直(z平面)时,入射波耦合效应最显著,能够耦合进入目标腔体的电磁能量最多;当开口平面平行于入射波方向时,电磁脉冲耦合值相对较小。另外,值得注意的是,开口在任意位置时HPM耦合信号功率密度都比较大,达到了多种电子元器件的电磁损伤阈值级别。
3.3 开口大小对腔内电场的影响
入射波保持不变,开口位置设置在z平面,依次设置开口的大小为50×50、100×100、200×200、300×300和400×400,其他仿真条件设置不变。
对计算所得的数据进行整理计算,同样可以得到该仿真条件下不同位置处的平均功率密度和总的能量密度值。表3为开口大小(表中d表示开口边长)变化时C0 probe处的数据处理结果。从表中可以看出,开口尺寸对电磁脉冲耦合效应具有较大的影响。对于HEMP激励来说,开口尺寸越大,腔体内耦合信号越强,耦合的能量也就越多。对于HPM激励来说,其变化趋势略有不同,当开口尺寸由50增加到200时,腔内耦合能量显著增加,但当开口尺寸继续增大时,腔内耦合能量不但没有增加反而略微下降。这一现象的出现与耦合电磁波的频谱范围有关。HEMP激励波是一宽频电磁波,频率范围主要分布在0~1 GHz,当开口尺寸较小时,仅有小部分频谱分量能够耦合进入目标腔体内部,因而耦合能量较小。随着开口尺寸增大,越来越多的频谱分量能够耦合到腔体中,耦合能量显著增加。而HPM属于窄频信号,能量主要集中在载波频率f0附近,仿真时f0设置为6 GHz,波长为50 mm,当开口尺寸较小时,随着尺寸增加,耦合面积随之增加,腔体内的耦合能量也就不断增大;但当开口尺寸较大时,继续增大开口尺寸,耦合信号在腔体内的振荡过程会更为剧烈,振荡中从开口位置逃离的电磁能量逐渐增多,因而,此时随着开口尺寸增大,耦合能量不但不能继续增加,反而会略微下降。
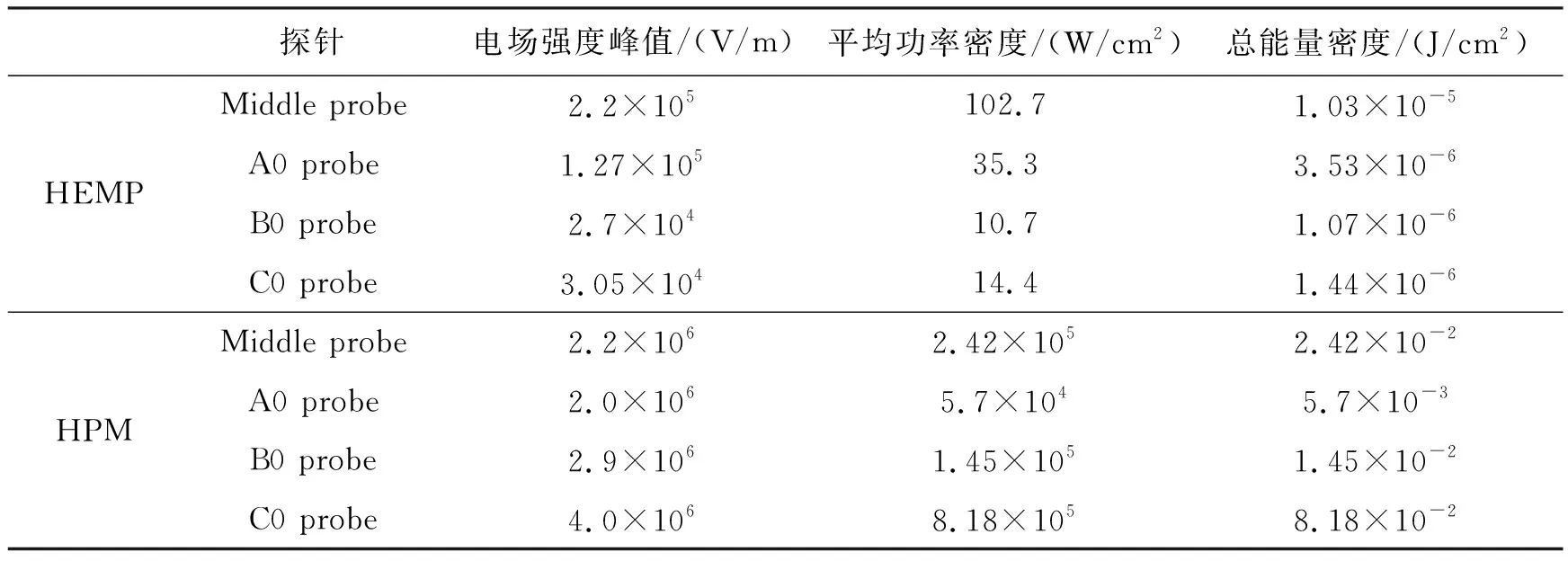
表1 电场强度探针测得信号的主要参数

表2 不同开口位置条件下耦合信号的主要参数

表3 不同孔缝大小条件下耦合信号的主要参数
3.4 开口长宽比对腔内电场的影响
保持激励波方向和大小不变,孔缝位置设置在z平面,固定开口面积,依次调节孔缝的尺寸为50×800、100×400、200×200、400×100和800×50,其他仿真条件设置不变。
与前面类似,表4给出了开口长宽比变化时C0 probe处的数据处理结果,表中Lx为腔体开口与入射电场极化方向平行的边长。从表中可以看出,对于两种强电磁脉冲,长宽比对耦合效应的影响具有不同的变化规律。对于HEMP激励来说,耦合功率密度随开口x方向边长的增加而减小,即腔体开口与入射电场极化方向垂直的边越长,腔体中耦合能量越大,这一现象反映了矩形孔缝耦合的极化特性。产生这一特性的原因在于矩形孔缝的特征频率发生改变,当与入射波电场的极化方向垂直的孔缝边长越长时,矩形孔缝的特征频率越小,导致能够进入到腔体内部的强电磁脉冲耦合能量也就越多。对于HPM,孔缝耦合的极化特性并不明显,当腔体开口长宽比改变时,腔内耦合信号值变化较小。这是因为HPM的激励波频率相比于孔缝特征频率大得多,受矩形孔缝的影响较小。
4 结论
HEMP和HPM两种强电磁脉冲都能够通过孔缝耦合进入腔体内部,从而给腔内电子元器件造成干扰甚至破坏。对于HEMP,当开口平面与激励波入射方向垂直时,耦合效应最强;同时,开口的尺寸越大、腔体开口与入射电场极化方向垂直的边越长,腔体中耦合能量越大。但由于HEMP的耦合效应受孔缝的位置、大小以及长宽比影响较大,因此合理控制孔缝的位置、大小以及长宽比可以减小耦合进入腔体内的能量,在一定程度上削弱HEMP的破坏效能。对于HPM,在相同条件下其耦合效应要明显强于HEMP,并且在孔缝达到一定尺寸后,耦合效应受孔缝的大小和长宽比的影响较小,仅受孔缝位置的影响。当开口平面与激励波入射方向垂直时,其耦合效应最显著;在开口平面平行于HPM入射方向情况下,耦合效应最弱,但此时耦合进入腔体内的能量还是能很容易达到多种电子元器件的电磁损伤阈值级别,因而HPM具有很强的破坏效能。

表4 不同孔缝长宽比条件下耦合信号的主要参数
