高超声速飞行器保预设性能的反演控制方法*
2020-02-07李小兵赵思源卜祥伟何阳光
李小兵,赵思源,卜祥伟,何阳光
(1. 空军工程大学 防空反导学院, 陕西 西安 710051; 2. 空军工程大学 研究生院, 陕西 西安 710051)
高超声速飞行器(Hypersonic Flight Vehicles,HFV)作为一种新型的临近空间战略武器装备,已成为近十年来的研究热点。控制系统面临着系统的不确定性、复杂子系统与非线性模型的耦合,因此HFV的飞行控制器设计成为一个具有挑战性的研究课题[1-3]。同时,由于系统的不确定性,控制增益信号一般是未知的,给控制器的设计带来了很多困难[4-5]。传统的仿射模型控制器设计方法不能处理HFV非仿射模型,对控制器的动态性能和稳态精度提出了更高的要求[6-8]。
HFV在大跨度飞行包络范围内需要完成许多复杂的任务,因此有必要设计一种有效的控制方法。然而,复杂的飞行环境、未知的外部干扰和模型的不确定性使得HFV的鲁棒控制具有挑战性[9-11]。为了解决HFV飞行过程中的不确定项和干扰问题,文献[12]并没有使用动态高阶微分器,而是设计了一种无模型跟踪控制器。文献[13]研究了HFV纵向运动模型的鲁棒控制,保证了对模型不确定性的鲁棒控制律。为了克服鲁棒控制通常过于保守的缺点,文献[14]设计了一种适用于HFV的滑模控制律。当模型参数受到扰动时,控制律仍能保证参考输入的稳定跟踪。文献[15]研究了高阶连续滑模控制器的设计,实现了HFV控制输入的连续切换,避免了控制输入高频抖振的影响。在文献[16-17]中,HFV容错控制是为了保证执行器故障的稳定跟踪而设计的。文献[18]介绍了最小学习参数算法,估计了神经网络权值矩阵的范数,降低了在线学习量。文献[19]对模型进行了变换,将HFV模型分解为速度子系统和高度子系统,将高度子系统转化为等效的纯反馈系统,避免了传统反演方法的缺点,引入了最小参数学习方法,减小了计算量。
国内外对HFV仿射控制的研究虽取得了很大的成果,但实际模型是非仿射的,且不宜被仿射化。由于上述控制策略只保证了控制系统的稳态性能,因此不考虑系统的动态性能。并且,对HFV高速飞行和控制系统快速飞行的动态性能要求也不能满足。文献[6] 设计了HFV预设性能反演控制器,因为控制律对预设性能函数的初值选择提出了更高的要求,虽然速度和高度跟踪误差限制在预设范围内,但可用性和实时性较差。在文献[20]中,通过组合隐藏函数和均值定理,对仿射模型进行了变换,并通过RBF神经网络对未知函数进行了逼近,提出了一种自适应变结构控制的非仿射控制方法。文献[21]通过泰勒公式将HFV非仿射模型转化为仿射模型,设计了自适应模糊神经非仿射控制律。本文利用中值定理[22]对HFV的非仿射模型进行变换,然后利用神经网络估计未知函数,同时引入Nussbaum函数来处理以前未知的控制方向问题。
本文设计了一种新型HFV纵向运动跟踪控制器,该控制器是基于HFV非仿射模型提出的保证预设性能的反演控制策略,旨在保证跟踪误差被限定在预设区域内。控制器的设计是建立在非仿射模型上的,这避免了模型简化过程中的不确定并保证了控制策略的可行性。所设计的预设性能控制器实现了准确地对参考输入的稳定跟踪。由于控制策略的建立与准确的飞行器模型和函数估计值无关,因此增强了系统鲁棒性的同时降低了在线计算量。最后,通过仿真实验验证了控制策略的实用性和优越性。
1 问题描述
1.1 HFV纵向平面运动学方程
本文采用Bolender和Parker的HFV面向控制的非线性模型[23-24],其纵向平面受力情况图1所示。HFV上所受的空气动力可以表示为升力L、推力T、阻力D和俯仰力矩M,推力T作用在飞行器机体轴线上。同时,图1也表示了HFV的航行速度V,航行高度h,航迹角γ,俯仰角θ,攻角α=θ-γ。由标准拉格朗日方程推导出的HFV纵向动力学模型可以表示为如下形式:
(1)
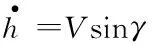
(2)
(3)
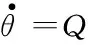
(4)
(5)
(6)
(7)
其中,部分系数表达式如下:
(8)
L、T、D、M只表示力的大小,其拟合式如下:
(9)
(10)
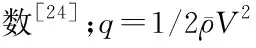
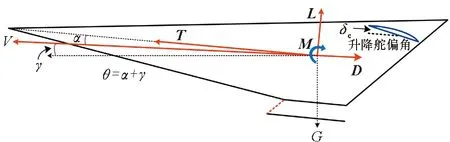
图1 HFV受力示意图Fig.1 Force map of HFV model
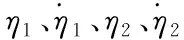
HFV巡航段飞行速度V的变化相对于俯仰角θ和俯仰角速率Q近似为慢变量[9],为了便于设计控制器,通常将HFV模型分解为速度子系统(见式(1))和高度子系统(见式(2)~(5)),并分别进行控制器设计。
假设1所有的参考指令和它对于时间的一阶及二阶导数是有界连续的。
1.2 预设性能分析
定义连续函数ρ(t):R+→R+,若同时满足以下两个条件[25],则该连续函数可被称为预设性能函数。
1)ρ(t)是严格单调递减的正函数;
基于上述定义,本文设计如下预设性能函数:
ρ(t)=(ρ0-ρ∞)e-lt+ρ∞
(11)
其中,ρ∞≤ρ(t)≤ρ0,ρ0>ρ∞>0,l>0为待设计参数。
跟踪误差e(t)需要满足下述定义不等式:
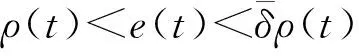
(12)
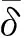
这就保证e(t)具有满意的动态性能与稳态精度,且ρ(t)是有界的。在设计控制系统的过程中,直接对不等式约束式(12)进行处理的难度非常大,因此可以先将不等式约束转化为等式约束再进行设计,这里定义一个误差转换函数S(ε(t)),则
(13)
将S(ε(t))选取为如下形式:
(14)
显然,S(ε(t))具有严格递增性,于是其逆函数ε(t)的一阶动态方程为:
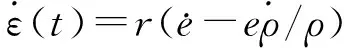
(15)
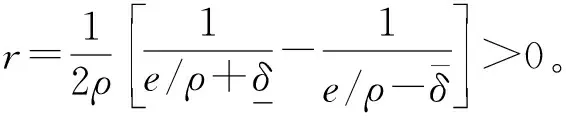
(16)
(17)
1.3 RBF神经网络
引入如下径向基函数(Radial Basis Function, RBF)神经网络用来逼近模型不确定项:
φ(Z)=WTS(Z)
(18)
式中,φ∈R和Z∈Rn分别是神经网络的输出和输入,W∈Rn为权值向量,S(Z)=[S1(Z),…,Sn(Z)]T是径向基函数。通常情况下,将Si(Z)选取成如下高斯基函数:
(19)
式中,ai∈Rn为高斯基函数中心向量大小,bi∈R+为高斯基函数的宽度。
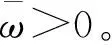
φ(Z)=W*TS(Z)+Δ(Z)
(20)
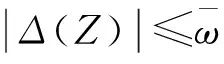
(21)
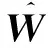
2 控制器设计与稳定性分析
2.1 指令滤波器
当采用反演控制方法设计控制器时,“微分项爆炸问题”必然会发生。本文将引入一组指令滤波器,而不是反复求导[26]。其表达形式如下:
(22)
其中,ηω>0为待设计参数,δi-1为虚拟控制信号。
定义估计误差信号ϑi为如下形式:
ϑi=ωi-δi-1,i=2,3,…,n
(23)
则
(24)
zi=xi-δi-1,i=2,3,…,n
(25)
式中,xi为实际信号,在后文的设计中i代表HFV纵向模型中的γ,θ,Q。
2.2 速度控制器设计与稳定性分析
由于速度的动态变化比高度系统慢,所以当速度变化时,可以认为高度和高度角已经达到了其稳定状态[4]。因此将速度子系统表达式写为如下形式:
(26)
式中,fV是未知的不可微非仿射连续函数,Φ和V为速度子系统的输入和输出。根据中值定理,将式(26)改写为如下形式:
(27)
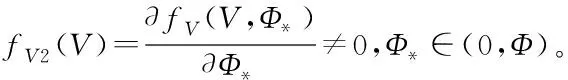
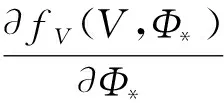
ρV(t)=(ρV0-ρV∞)e-lVt+ρV∞
(28)
根据式(12)可以得到:
(29)
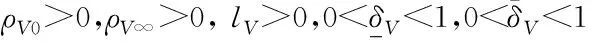
将式(29)转化为:
(30)
综合式(17)和式(27),将转换函数zV(t)对时间求导可得:
(31)
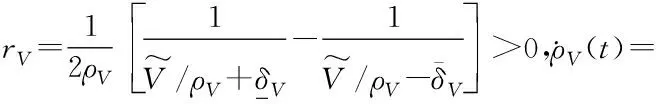
定义Lyapunov函数为:
(32)
式中,νV为动态信号,λV0为待设计参数。对式(32)求导可得:
(33)
根据Young′s不等式以及假设2,有
(34)
将式(34)代入式(35),可得:
(35)
令
(36)
由于μV0(V)是非负的连续函数,则必存在一个连续的函数φV(ZV),使得
zVφV≤zVφV(ZV)+λV
(37)
其中,ZV=[V,zV,rV]T∈R3,λV>0为待设计参数。
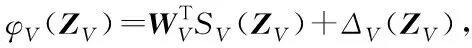
将速度控制律Φ设计为:
(39)

选取如下Lyapunov函数:
(40)
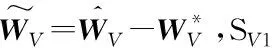
对式(40)求导可得:
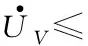
(41)
由于
(42)
则式(41)可进一步写成
(43)
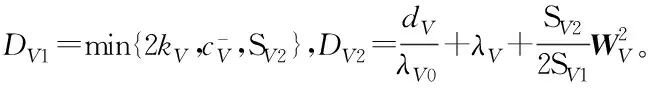
(44)
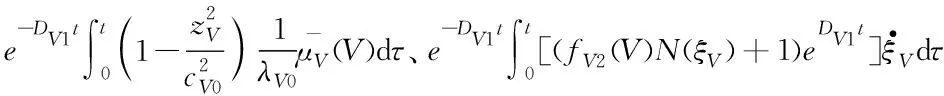
2.3 高度控制器设计与稳定性分析
为了便于控制器设计,根据式(2)~(5)将HFV高度子系统改写为如下形式:
(45)
其中,fh、fγ、fθ和fQ是未知的不可微非仿射连续函数。根据中值定理将式(45)改写为:
(46)
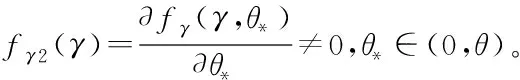

假设4参考指令href和它对于时间的一阶及二阶导数是有界连续的。
ρh(t)=(ρh0-ρh∞)e-lht+ρh∞
(47)
根据式(12)可以得到
(48)
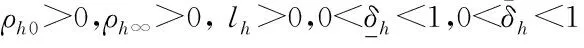
将式(48)转化为:
(49)
综合式(17)和式(46),将转换函数zh(t)对时间求导可得:
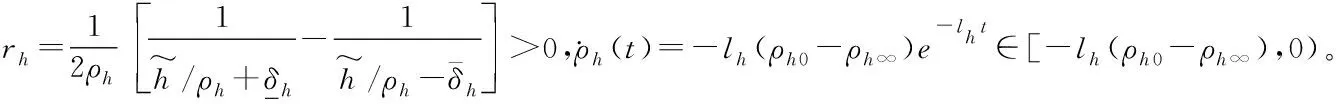
定义Lyapunov函数
(51)
式中,νh为动态信号,λh0为待设计参数。对上式求导可得:
(52)
根据Young′s不等式及假设3,有
(53)
将式(53)代入式(52),可得:
(54)
令
(55)
由于μh0(h)是非负的连续函数,则必存在一个连续的函数φh(Zh),使得
zhφh≤zhφh(Zh)+λh
(56)
其中,Zh=[h,zh,rh]T∈R3,λh>0为待设计参数。
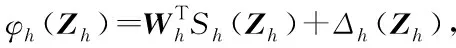
将虚拟控制律γd设计为:
(58)
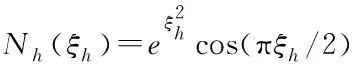
选取如下Lyapunov函数
(59)
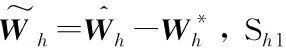
对式(59)求导可得:
(60)
由于
(61)
则式(60)可进一步写成
(62)

(63)
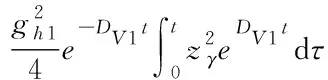
考虑系统式(46),结合指令滤波器,可得:
zγ=γ-γd=γ-ωγ+ϑγ
(64)
进一步,有
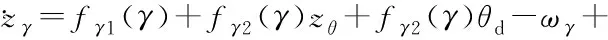
(65)
定义Lyapunov函数
(66)
对上式求导可得:
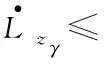
(67)
类似于速度控制器设计,可以得到
(68)
令
φγ=fγ1(γ)+ηω(ωγ-γd)
(69)
存在一个未知的连续函数φλ(Zλ),使得:
(70)
其中,Zγ=[γ,zγ,ωγ,γd]T∈R4,λγ为待设计参数。
将式(70)代入式(68),可得:
(71)
将虚拟控制律θd设计为:
(72)
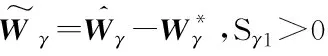
选取如下Lyapunov函数
(73)
对上式求导,并综合考虑Uh和Lzγ可得:
(74)
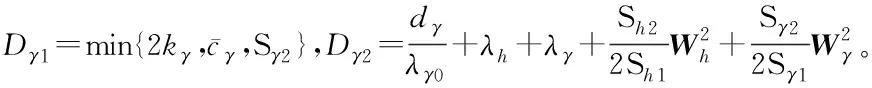
对式(74)两边同乘e-Dγ1t并积分,可得:
(75)
虚拟控制律Qd的设计过程及稳定性证明均和以上步骤类似,这里不再赘述。 直接给出将虚拟控制律Qd设计为如下形式:
(76)
考虑系统式(46),结合指令滤波器,可得:
zQ=Q-Qd=Q-ωQ+ϑQ
(77)
进一步,有
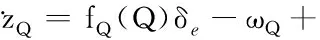
(78)
定义Lyapunov函数
(79)
对上式求导可得:
(80)
令
φQ=ηω(ωQ-θd)
(81)
存在一个未知的连续函数φQ(ZQ),使得:
(82)
将实际控制律δe设计为:
(83)
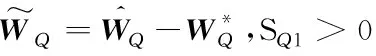
选取如下Lyapunov函数
(84)
对上式求导,并综合考虑Uθ和LzQ可得:
(85)

对式(85)两边同乘e-DQ1t并积分,可得:
(86)
(87)
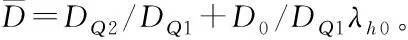
3 仿真与分析
针对HFV动力学模型进行速度与高度的闭环仿真实验。速度与高度参考输入均由图3所示的二阶参考模型给出。该二阶参考模型的传递函数为[27]:
(88)
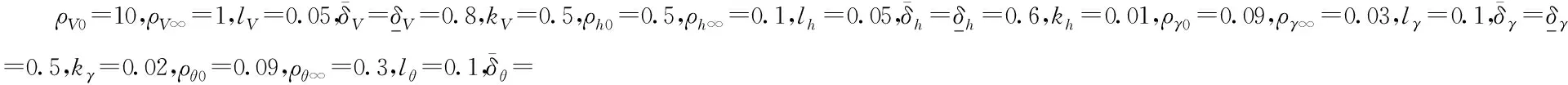
HFV飞行包线的刚体取值范围可以见文献[28]。 仿真中,HFV的初始状态取值见表1。
通过MATLAB/Simulink搭建控制系统,采用步长为0.01 s的四阶Runge-Kuta法进行验证控制方法的有效性。要求临近空间巡航阶段HFV在速度阶跃Vd=100 m/s,高度阶跃hd=100 m作用下。控制任务是要求系统输出能够准确跟踪给定的速度和高度参考指令并保证跟踪误差稳定在预设的区域内。为了检验控制律的鲁棒性,仿真中给HFV模型气动系数存在±40%的摄动量,定义:
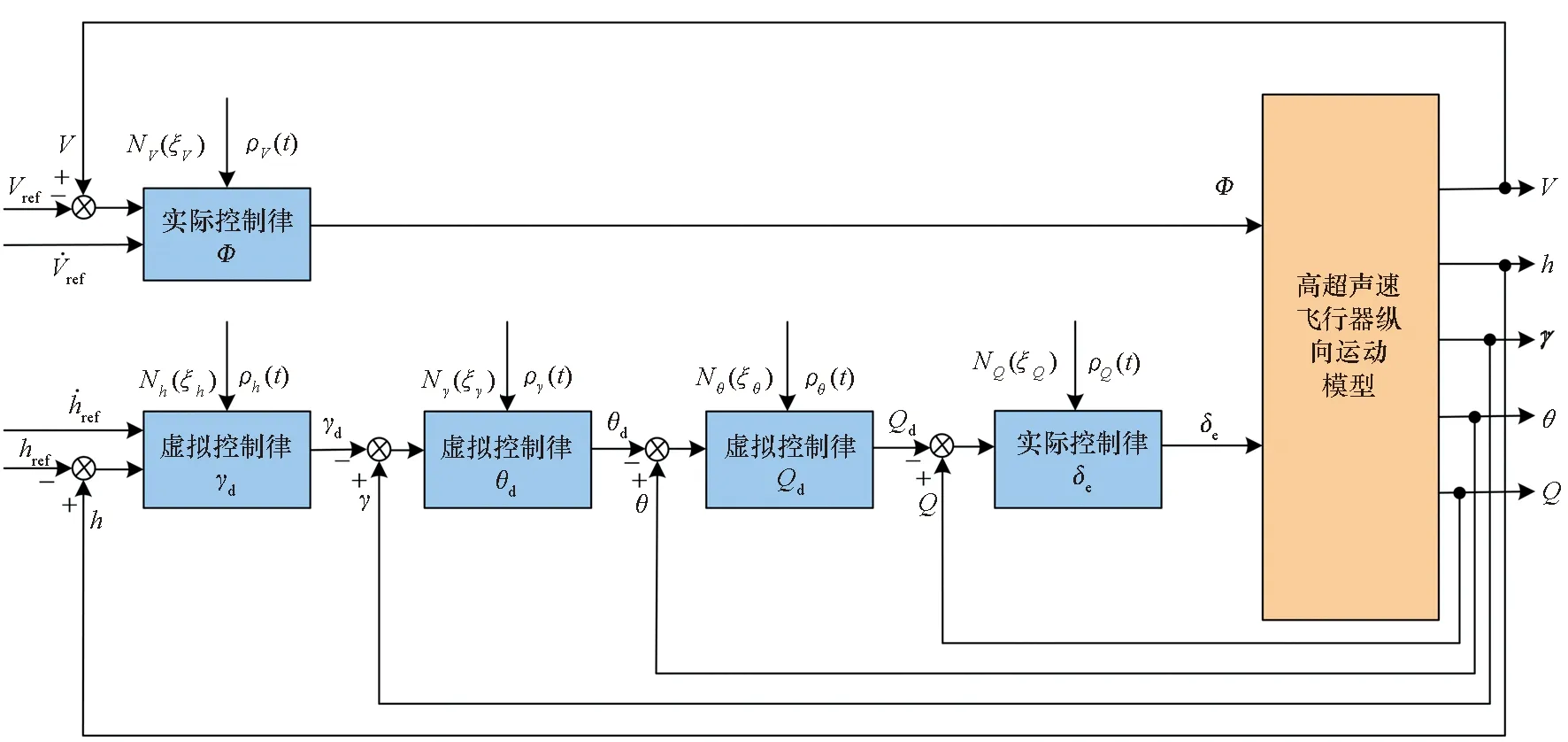
图2 HFV控制结构图Fig.2 Control structure of HFV
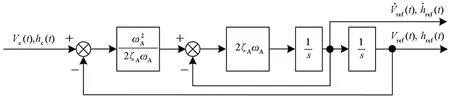
图3 参考输入二阶模型结构Fig.3 Second-order model structure of reference
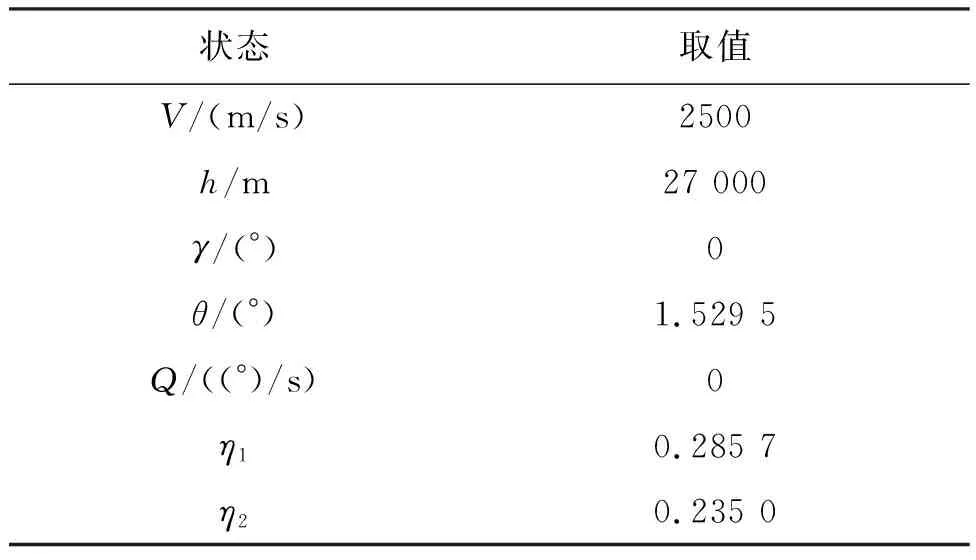
表1 HFV的状态初值
(89)
式中,C0表示HFV气动系数的标称值。
为了验证本文所提方法具有更好的使用价值,将保预设性能(Guarantee Prescribed Performance, GPP)方法与文献[29]中神经反演控制(Neural Network Backstepping, NNB)方法进行对比仿真,仿真结果如图4~9所示。在模型参数摄动的情况下,本文设计的GPP方法能保证速度跟踪误差和高度跟踪误差的稳态精度和较好的动态性能,实现速度跟踪误差的小超调收敛和高度跟踪误差的零超调收敛。由图4~5可知,与文献[29]中的NBB方法相比,该控制器的速度和高度跟踪误差能更快地收敛到零,这表明该控制器比文献[29]中的NBB方法具有更好的动态性能;图6~9显示了两个控制器的姿态角、弹性状态和系统输入都是平滑的,没有高频抖振。如此,设计的控制器可以保证速度跟踪误差的小超调收敛和高度跟踪误差的零超调收敛。同时,控制律对参数的存在具有鲁棒性,控制系统的动态性能和稳态精度满足预定性能的要求。
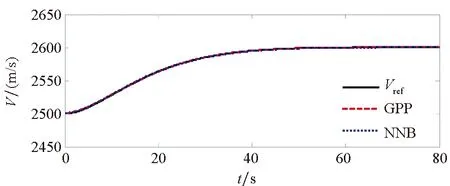
(a) 速度跟踪曲线(a) Velocity tracking curve
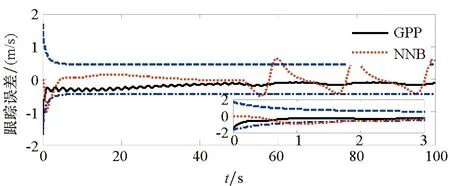
(b) 速度跟踪误差(b) Velocity tracking error图4 速度跟踪响应Fig.4 Velocity tracking performance
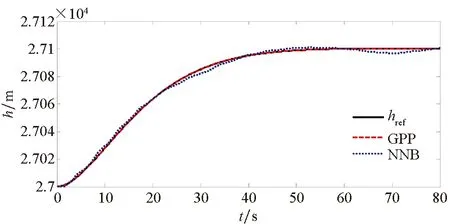
(a) 高度跟踪曲线(a) Altitude tracking curve
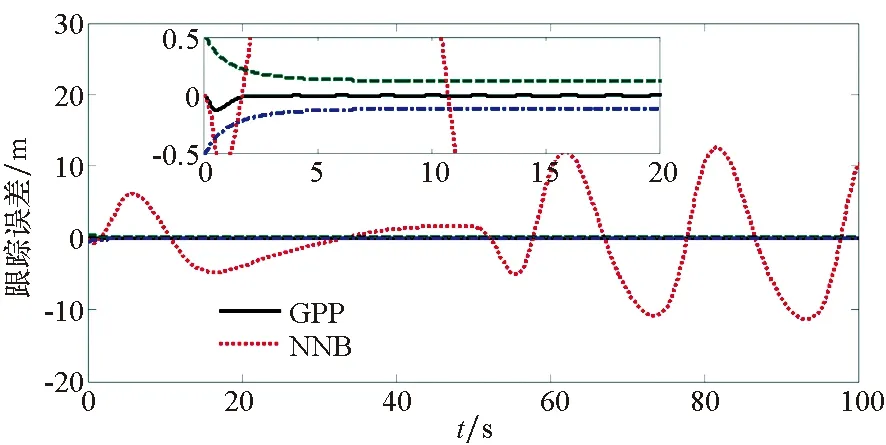
(b) 高度跟踪误差(b) Altitude tracking error图5 高度跟踪响应Fig.5 Altitude tracking performance

(a) 航迹角曲线(a) Path angle curve
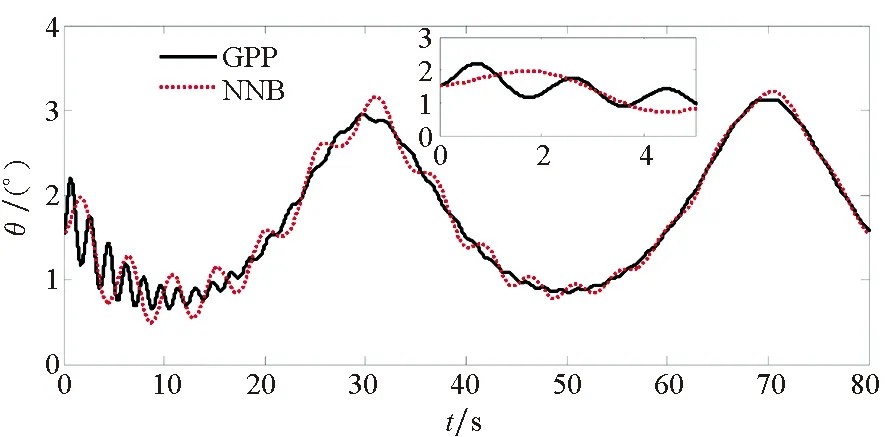
(b) 俯仰角曲线(b) Pitch angle curve
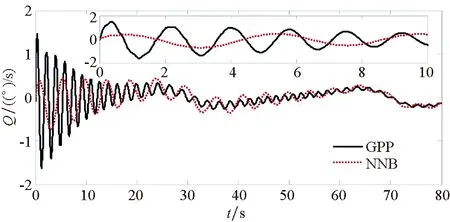
(c) 俯仰角速度曲线(c) Pitch rate curve图6 高度角曲线Fig.6 Altitude angle curve
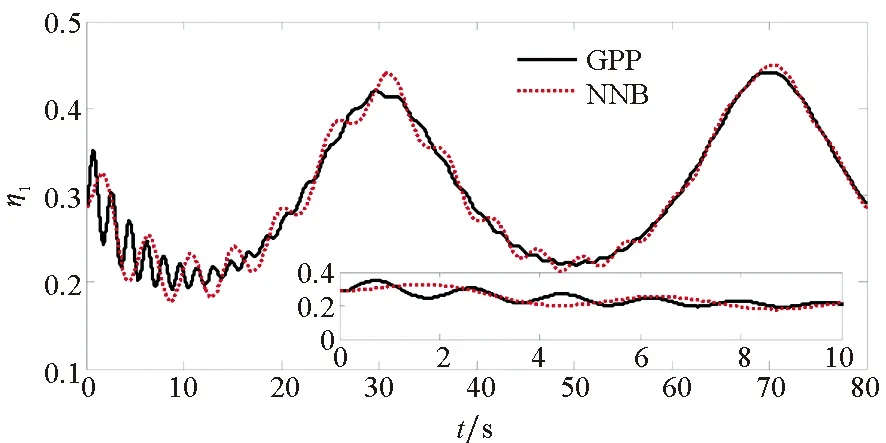
(a) 第一弹性状态(a) The first flexible state
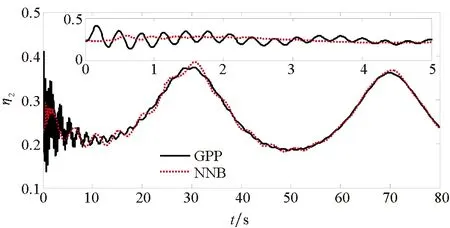
(b) 第二弹性状态(b) The second flexible state图7 弹性状态Fig.7 The flexible states
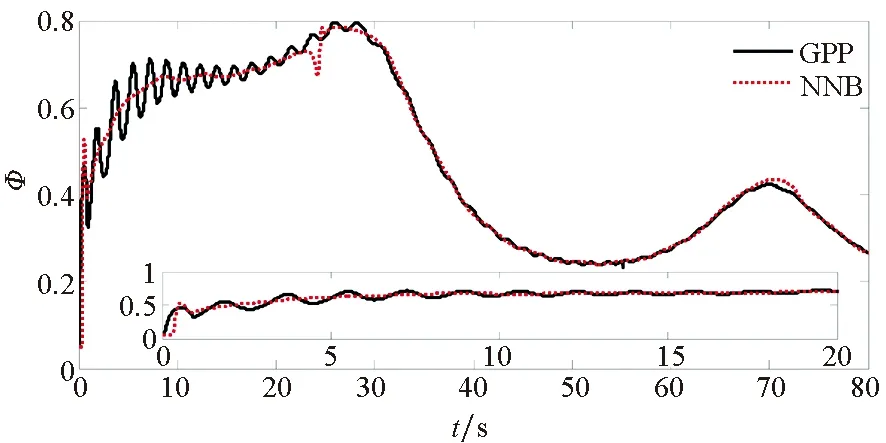
图8 燃料空气比Fig.8 Flue-to-air ratio
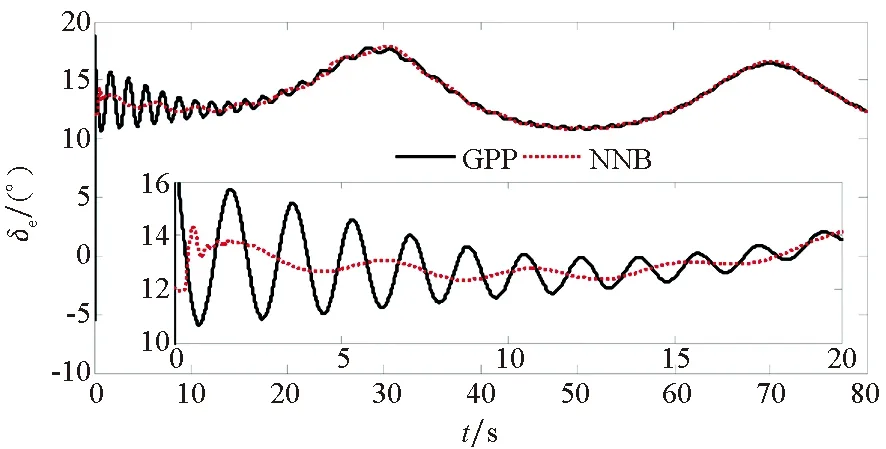
图9 升降舵偏角Fig.9 Elevator declination
4 结论
本文在反演控制方法的结构下,为HFV设计了一种保证预设性能的控制方法。通过引入预设性能函数来限定跟踪误差的预设范围,控制律的设计基于HFV的非仿射模型,保证了预期的动态性能。所设计的控制器不再需要精确的模型以及控制增益的信号,其鲁棒性和实用性得到了很大的提升。通过引入动态信号,克服了原模型中存在未建模的动态,并引入一组指令滤波器,有效地规避了反演控制方法中的反复求导,运用Lyapunov方法证明了所有闭环系统的稳定性。最后,数字仿真结果表明了所设计的控制器对参考信号跟踪的准确性及较好的可行性。
