基于集成评价体系的抛掷爆破效果评价

赵红泽，王宇新，李 淋，郭 帅，郭心灵

(1.中国矿业大学(北京)能源与矿业学院，北京 100083；2.中国矿业大学(北京)共伴生能源精准开采北京市重点实验室，北京 100083；3.中国矿业大学(北京)煤炭安全开采与地质保障国级实验教学示范中心，北京 100083)

0 引 言

随着露天矿的迅速发展，涌现出以黑岱沟露天矿为代表的30 Mt/a特大型露天矿，而产量的不断加大，也对生产工艺的接续提出了更高的要求。抛掷爆破作为抛掷爆破-拉斗铲无运输倒堆工艺的基础环节，具有爆破煤层上覆土岩、将部分土岩直接倒堆至采空区、减少拉斗铲倒堆作业量、提高生产效率的重要作用[1]，合理的抛掷爆破效果不仅能最大限度地减少拉斗铲作业量、满足生产作业要求、实现企业利益的最大化，而且还影响着爆破现场人员和机器设备的安全以及生态环境。在实际的抛掷爆破工程中，需要对爆破效果进行准确的评价，进而对后续爆破参数优化与方案比选提供合理的依据。

针对爆破效果评价，国内学者通过爆破后部分指标运用灰色关联、模糊综合评价、BP神经网络、层次分析法等运筹学原理对爆破效果进行定量或定性的评价，如吴明等[2]以爆破成本等3个要素为一级指标，爆堆形态等8个要素为二级指标运用层次分析法和模糊数学法对平朔东露天矿进行爆破效果评价；马力等[3]将炸药单耗、松散系数、极限振速、有效抛掷率4个指标，通过模糊数学原理，进行黑岱沟露天矿爆破效果评价；韩亮等[4]通过运用BP神经网络将爆堆形态的8个参数及Weibull控制参数及松散系数为样本进行爆堆形态的预测；赵国彦等[5]通过模糊综合评价和层次分析法相结合，优化了权重的大小，减小了权重赋值的主观性，以黄沙坪铅锌矿中深孔爆破为实例，建立以爆破安全参数等4个单元、炸药单耗等15项评价指标为主的爆破评价模型。上述学者虽采取不同的方法进行爆破效果的合理评价，但在对评价体系赋权时存在单指标、主观性判断、未进行多体系纵向比较等缺陷，使得对评价结果不够客观。

综上所述，针对抛掷爆破效果多影响因素进行评价，本文优化选取炸药单耗、有效抛掷率、松散系数、抛掷距离、极限振速、松方体积、延米爆破7个评价指标，运用层次分析(AHP)-灰色关联分析法和层次分析(AHP)-熵权法，将单一方法和集成方法横向比较，进行定量分析，从而得出更加精准的爆破效果评价。

1 相关理论介绍

1.1 层次分析法

层次分析法是一种针对于多个目标方案的决策与分析方法，依据目标方案的重要性进行两两相互比较，建立判断矩阵，通过矩阵运算得出最大特征值及最大特征向量，进而得出不同方案下指标权重，为方案最优化提高可靠依据[6-7]。

1.1.1 构建判断矩阵

采用一致性矩阵，将相同层元素两两进行比较，而不是采取同层共同比较，通过1～9级标度来构造判断矩阵。aij(i,j=1,2,3…,n)为同层元素中Ai相对于Aj的重要程度级数，以1～9级标度及其倒数来具体取值，表示方法见表1。

1.1.2 评价指标权重的计算

令判断矩阵的最大特征值为λmax,相对于的特征向量为D,判断矩阵A各行元素相乘开n次根号，归一化处理后得到权重向量Wj=(W1,W2，…Wn),计算公式见式(1)。

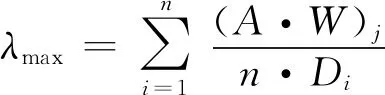
(1)

1.1.3 评价指标权重的计算

为保证决策的合理性，需对判断矩阵进行一致性检验，计算公式见式(2)。

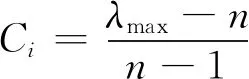
(2)

式中，Ci为一致性指标。

一致性比例计算见式(3)。

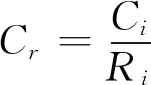
(3)

式中：Cr为一致性比例；Ri为一致性指标。

当Cr<0.1时认为判断矩阵的一致性可以被接受。随机一致性指标Ri见表2。

表1 各级标度含义

表2 随机一致性指标Ri

1.1.4 理想最优方案确定

1.2 灰色关联分析法

灰色关联分析的基本原理是通过权衡统计序列各因素间发展的相似和相异程度来计算系统中关联程度的大小[6-7]，序列曲线的几何形状相似程度越接近，相关程度就越大，并且该方法对于样本容量以及样本间规律性要求较低，具体计算量小精度高的特点。灰色关联度计算步骤如下。

1) 用极值法对数据进行无量钢化处理，处理后于理想数据组合得到矩阵，见式(4)。

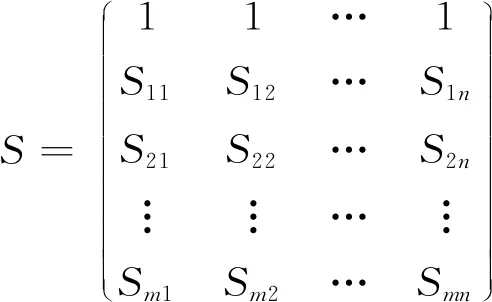
(4)

2) 记S0为参考数列，则Si的第j个指标与参考数列S0的第j个指标关联系数为βi(j)(i,j=1,2…,n),计算公式见式(5)。

βi(j)=

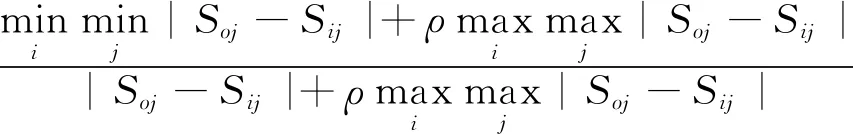
(5)

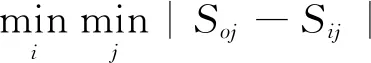
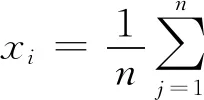
1.3 熵权法

在原始数据归一化处理后得到矩阵Sij,熵权法求权重方法如下。

1) 计算第j个评价指标的熵见式(6)。

(6)

式中，指标比重tij计算公式见式(7)。

(7)

2) 计算第j个评价指标的熵权ω见式(8)。

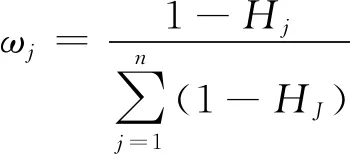
(8)

2 集成评价体系

集成评价方法是指将多个的评价方法通过事先检验，通过某种算法进行融合进而成得到一种新的集成评价方法，本文运用Kendall秩相关系数的方法对集成后的两组评价方法分别进行一致性检验，当伴生概率p小于显著性水平α时[8]，即可认为两种评价方法可以集成。

2.1 灰色-层次分析法评价体系

在灰色关联分析法中，分辨系数ρ的取值统一赋值为0.5，并未考虑到样本指标权重的差异，将所有样本认为同等重要，使得评价结果的严谨性、可信度均受到影响。采用主观评价法层次分析法与客观评价法灰色关联分析法集成，兼顾主客观因素，通过优化分辨系数ρ值，选取最优方案。

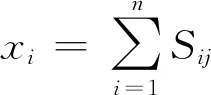
2.2 熵权-层次分析法评价体系

熵权法与层次分析法评价方法均是先确定各自的指标的权重，熵权法是根据客观数据而得到指标权重，但却不能充分的翻译专家的意见及决策者的决定，有时所得结果与实际差距较大。层次分析法设计依据主观专家经验而得到指标权重，但无法避免主观随意性的缺陷。对于两种评价方法的集成，可考虑对指标权重的集成βj。

记由熵权法求出m个评价指标的权重为ωAi,有层次分析法得出的m个评价指标的权重为ωBj,集成后综合评价指标中权重为βj(0≤α≤1)，计算公式见式(9)。

βj=αωAj+(1-α)ωBj

(9)

3 实例分析

本文以某露天矿抛掷爆破为实例，通过优选爆破评价数据，选择炸药单耗、有效抛掷率、松散系数、最远抛掷距离、最大振速、松方体积、延米爆破量7个评价指标，爆后效果图见图1，抛掷爆破效果评价体系见图2。

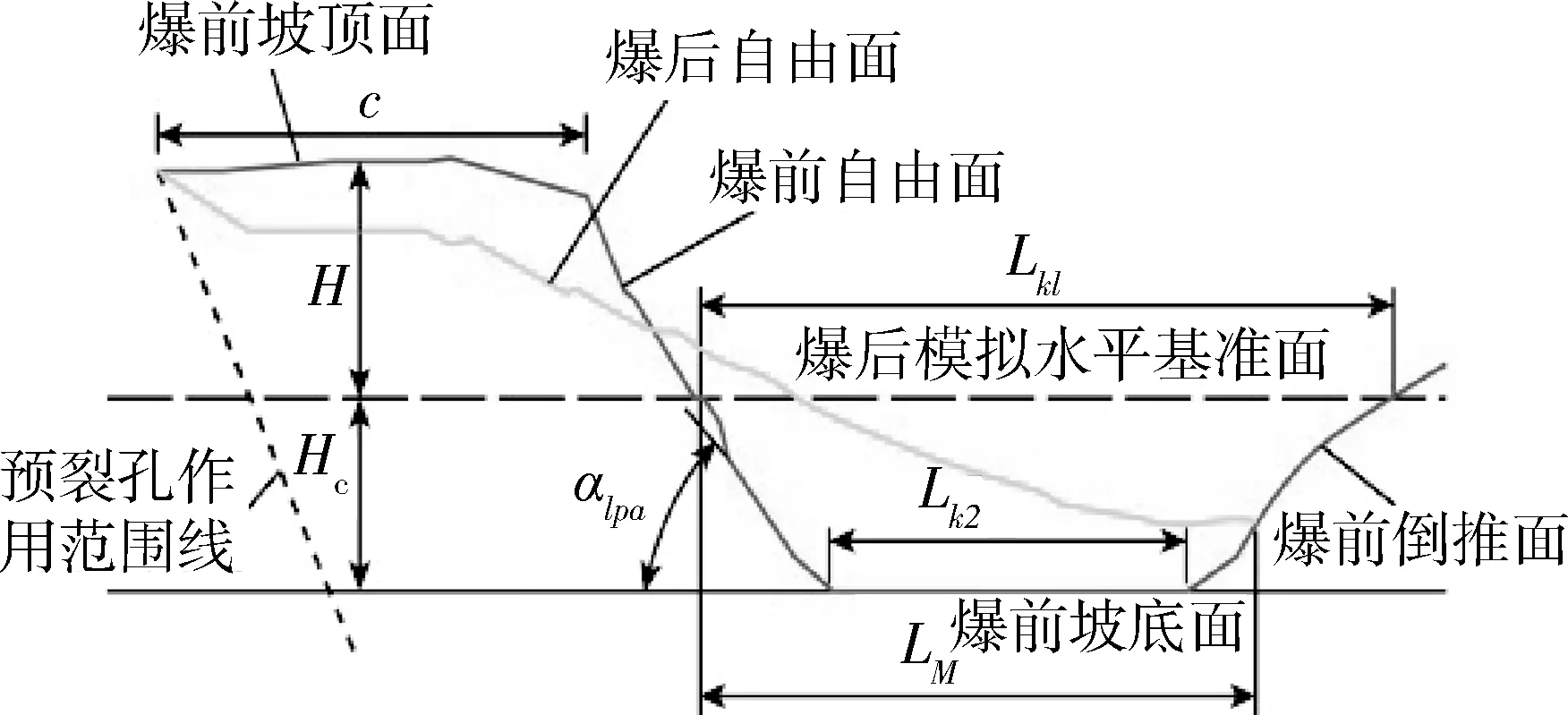
图1 抛掷爆破爆后效果图

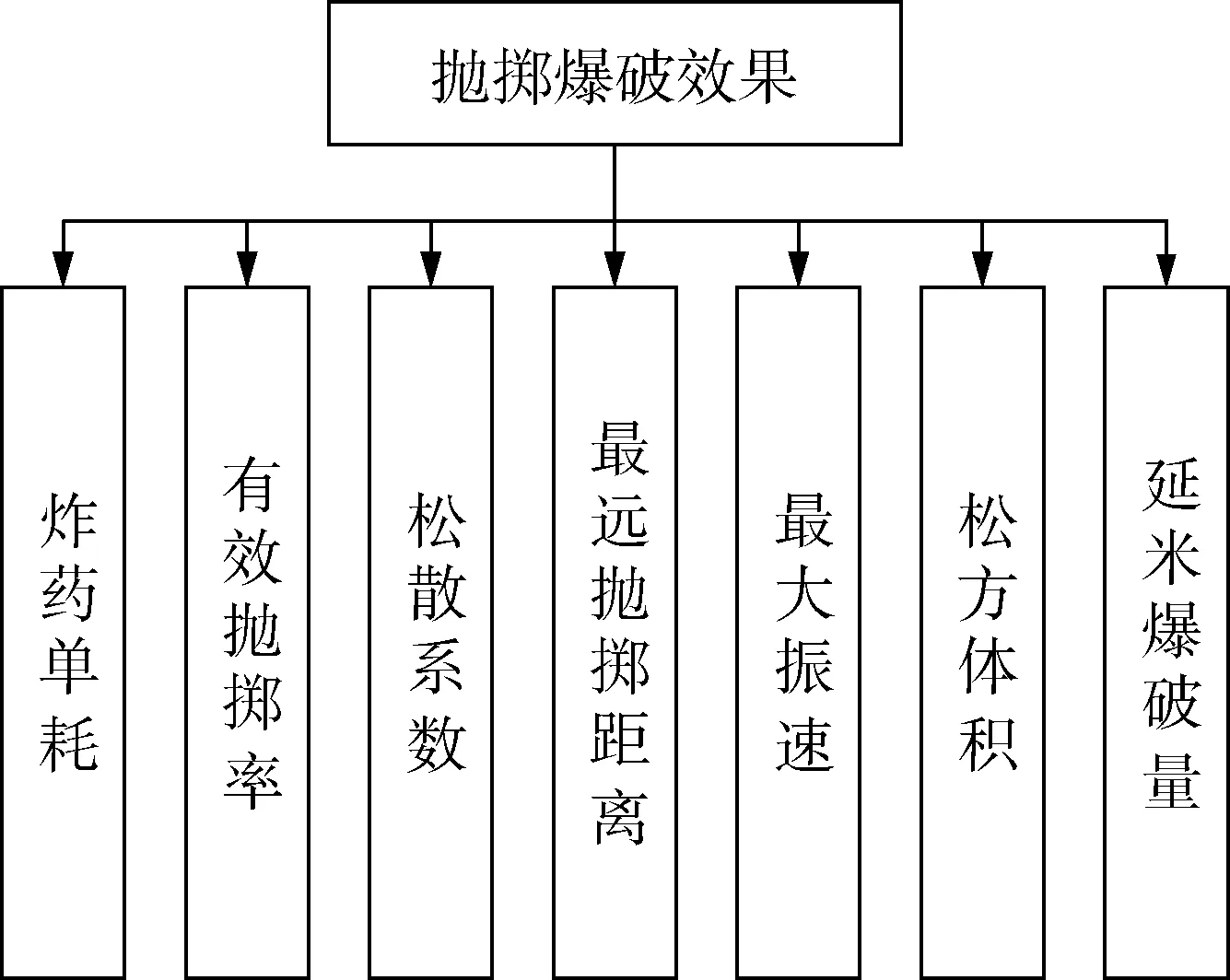
图2 抛掷爆破效果评价体系

3.1 抛掷爆破效果评价

根据图2，选取2018年不同有效抛掷作业中的10个爆堆剖面，运用上述评价方法，通过Matlab数据处理对10次爆破效果做出效果评价并排序。具体指标数据见表3。

3.2 层次分析法评价抛掷爆破效果

1) 由专家对同层爆破效果参数重要性进行相互比较，得到判断矩阵A，见式(10)。

(10)

2) 计算判断矩阵A的最大特征值λmax及相应的特征向量D，见式(11)和式(12)。

λmax=7.1445

(11)

D=(0.355 6 0.225 8 0.580 1 0.332 7

0.110 0 0.163 4 0.580 1)

(12)

3) 计算的CI=0.024 1；查表的RI=1.32；CR=0.018 2<0.1,一致性检验通过；特征向量标准化后，指标权重为ω，见式(13)。

ω=(0.151 5 0.096 2 0.247 1 0.141 7

0.046 9 0.069 6 0.247 1)

(13)

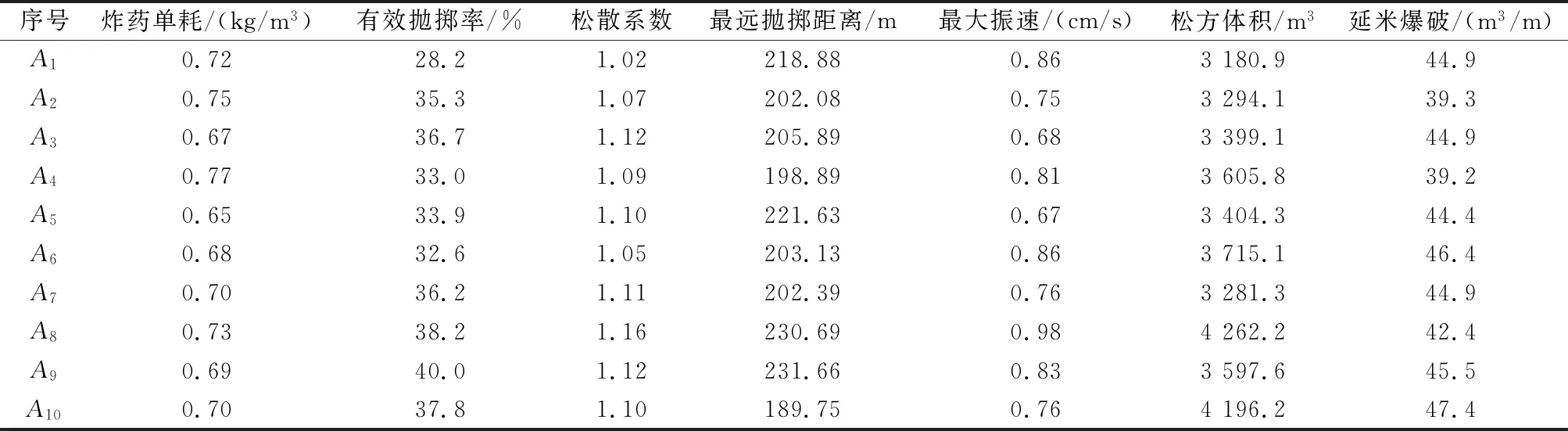
表3 10次抛掷爆破评价指标统计值

4) 计算各抛掷爆破效果的评价值x见表4，则10次抛掷爆破效果优劣排序为：A8，A9，A10，A7，A3，A6，A5，A1，A4，A2。

3.3 灰色关联分析发评价抛掷爆破效果

1) 确定理想抛掷爆破指标参数R0。

2) 计算关联系数矩阵(ρ=0.5)，见式(14)。

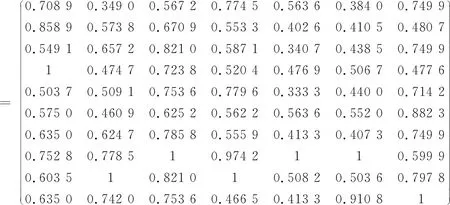
(14)

3) 计算各抛掷爆破效果方案与理想方案的关联度大小X见表5，则10次抛掷爆破效果优劣排序为：A8，A9，A10，A6，A4，A7，A3，A1，A5，A2。

3.4 熵权法评价抛掷爆破效果

1) 计算指标熵权ω,见式(15)。

ω=(0.134 9 0.088 9 0.101 7 0.146 4

0.169 4 0.218 3 0.140 4)

(15)

2) 计算各抛掷爆破效果方案的评价值X,见表6，则10次抛掷爆破效果优劣排序为：A8，A9，A10，A6，A4，A1，A7，A3，A5，A2。

3.5 灰色-层次分析法评价抛掷爆破效果

运用Kendall秩相关系数的方法对集成后的两组评价方法分别进行一致性检验，将灰色关联分析法得到的抛掷爆破效果排名按照自然顺序排列，得到层次分析法对应的排名。

1) 通过上述计算得到S=31。由于m=10，查表得到p=0.002 3;对于给定的显著性水平α=0.05，p<α，则两种方法一致性检验通过可以集成。

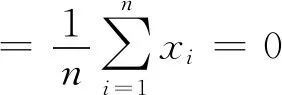
3) 新的分辨系数下各抛掷爆破效果方案与理想方案的关联度大小X见表7，则10次抛掷爆破效果优劣排序为：A8，A9，A10，A6，A7，A4，A3，A1，A5，A2。

3.6 熵权-层次分析法评价抛掷爆破效果

1) 上述计算得到S=27。由于m=10，查表得到p=0.008 3;对于给定的显著性水平α=0.05，p<α,则两种方法一致性检验通过可以集成。

2) 由上文得到的熵权法下指标权重为：αj1=(0.134 9 0.088 9 0.101 7 0.146 4 0.169 4 0.218 3 0.140 4)

层次分析法指标权重为：αj2=(0.151 50.096 2 0.247 10.141 70.046 90.069 60.247 1)。带入由乘数归一化法确定的模型的基础权重βj,则β=(0.208 40.087 80.256 40.211 40.086 7 0.155 3 0.354 4)。

3) 熵权-层次分析法下各抛掷爆破效果方案的评价值X见表8，则10次抛掷爆破效果优劣排序为：A8，A9，A10，A6，A7，A3，A4，A1，A5，A2。

表4 层次分析法计算评价值

表5 各方案灰色关联度

表6 熵权法计算评价值

表7 灰色-层次分析法下各方案灰色关联度

表8 熵权-层次分析法计算评价值

4 结果分析

将单一评价方法和集成评价方法对于抛掷爆破效果排序，见表9。通过比较熵权法与层次分析法排序结果可发现，爆破效果A4和A3变化较大，分析可得A4在炸药单耗参数一项中明显高于其他组爆破效果，爆破效果A3则在该指标上明显小于其他各爆破效果数据，在层次分析法中炸药单耗所占权重过大而在熵权中炸药单耗比重并不突出，可能在层次分析法中专家对于炸药单耗的重视造成两评价方法产生明显差异，熵权-层次分析法中集合了熵权分析中的客观事实依据和主观专家的判断，使得评价结果更加准确，相较单一评价方法更具有参考性和实用价值。

表9 各评价方法下抛掷爆破效果排序

通过对比灰色关联分析法与层次分析法下抛掷爆破效果的排序名次，可发现爆破效果A4的名次变化浮动较大，而在爆破参数中A4的炸药单耗值为10次爆破效果比较中最大值，而延米爆破值却为最小值，在灰色关联分析法中认为个指标权重相同，采用优劣互补的原则，分辨系数ρ统一选取0.5，而层次分析法中延米爆破权重高于所有指标，导致爆破效果A4在层次分析法中名次明显下降。而灰色—层次分析法中依据主观分析，重新确定分辨系数ρ,使得评价结果更加合理。

两类集成评价方法灰色-层次分析法和熵权层次分析法均融合了主观专家经验与客观数据，通过比较十组抛掷爆破效果评价排序较为一致，符合评价要求。

5 结 论

1) 从定量与定性结合的角度建立灰色-层次分析法和熵权-层次分析法集成的抛掷爆破评价体系，将单一评价方法与集成评价方法以及集成评价方法之间通过横向对比，集成评价体系较单一评价体系稳定性高，评价结果更相近，针对抛掷爆破评价结果更为全面、客观，对后续优化爆破参数具有强烈的参考价值。

2) 使用Kendall秩相关系数的方法对集成后的两组评价方法分别进行一致性检验，以确定集成方案的可靠性。灰色-层次分析法通过层次分析法所确定的评价对象的评价值来修正灰色关联中分辨系数ρ,以达到两种方法融合；熵权-层次分析按照两种方法指标权重的比例将两种评价方法进行拟合。

3) 本文所用模型虽是露天矿抛掷爆破效果评价模型，但集成评价思想与方法同样适合其他方案比选与指标评价，具有一定的参考意义。