考虑边坡渐进破坏的分区计算模型

2020-02-06蒋茂林陈文胜戴嘉宁李颖豪

交通科学与工程 2020年4期

蒋茂林，陈文胜，戴嘉宁，李颖豪

(长沙理工大学土木工程学院，湖南长沙 410114)

边坡稳定性分析是土木工程领域长期研究热点之一[1]，已有很多边坡稳定性分析和评估方法。其中，以极限平衡理论为基础的传统条分法(瑞典条分法、毕肖普条分法、Janbu 法、传递系数法等)[2−4]仍是最主要的边坡分析方法。条分法是先将复杂的滑体划分为若干竖直条块。然后，通过力的平衡条件求解，获得各条块上的相互作用力。最后，通过极限平衡理论，求解阻滑力(矩)和下滑力(矩)的比值，获得安全系数。但无论哪种条分法，都对条块受力进行了简化，使问题静定可解。简化后，问题可以解答，但会给结果带来不可避免的误差。

伴随计算机计算技术的发展，广泛应用的还有数值分析方法，如：有限单元法、离散单元法、无网格法、无界元法等。数值分析方法旨不同边界条件下，求解边坡的位移场、应力场、渗流场，并模拟边坡破坏过程，其精度主要取决于所采用的本构模型。因为计算原理的差异，不同的数值分析方法，所以会有不同的适用范围和特点。尽管分析边坡的方法愈来愈多，但因条分法具有直观、简便、易于理解等优点，是边坡稳定性分析和评估中应用最多的方法。

1 传统条分法的特点及渐进破坏

传统条分法无论是只适用于圆弧滑动面的瑞典条分法，还是可以适用于任意形式滑动面的Janbu 法、传递系数法等，都存在2 个特点：

1) 滑动面上所有点的安全系数相同，目的均为求解得到边坡整体安全系数。认为边坡的整体安全系数与各条块的局部安全系数处处相等，从而方便计算整体的安全系数。该特点同样延续至有限元的强度折减法中(对材料强度参数的折减，处处相等)。这一特点造成计算过程中认为：当边坡将要发生滑动破坏时，其滑面各处同时达到强度极限。

2) 传统条分法在计算各条块的阻滑力(矩)时，都是按照其峰值强度求得。实际上，边坡往往因内外界因素的作用，存在局部失稳区。而局部失稳区若按峰值强度计算，其阻滑力较工程实际大。这一特点认为：滑面各点安全系数处处相等，而导致后遗症。因为每一条块的特异性，其抗剪强度与下滑力均不同，所以各自达到峰值强度时刻不一致。当某一条块的下滑力超过其峰值强度时，该条块就会发生剪切破坏，承受能力会从峰值强度衰减到残余强度。故采用传统条分法进行分析和评估时，一般会高估边坡的承受能力，高估后果会导致工程、生态出现巨大损失。

大量工程实践表明：边坡发生失稳滑坡并不是一蹴而就。坡体总是由某一部位先失稳，失稳区域再逐渐扩大，最后导致边坡整体滑坡，因此坡体各局部的强度发挥是不一样的。最先失稳部位的强度最先达到极限，随后开始影响周边条块，失稳区逐渐扩展，该过程就是边坡的渐进破坏[5]。其本质是局部坡体先达到峰值强度而破坏，其抗剪强度由峰值变为残余值，之后超额剪应力转嫁给相邻土体，导致相继破坏，最终形成贯通滑面[6]。

为了实现对边坡渐进破坏的分析，得到合理的安全系数，本研究提出一种基于条分块体的模型，即分区计算模型。

2 边坡分区计算模型

分区计算模型通过条块间的力学分析，在考虑边坡渐进破坏的基础上，准确判断发生破坏或将要破坏的土体区域，将这部分土体按残余强度来计算阻滑力，而能抵挡下传推力的稳定土体按极限强度来计算阻滑力，最后对边坡进行稳定性分析。分区计算模型的示意图如图1 所示。

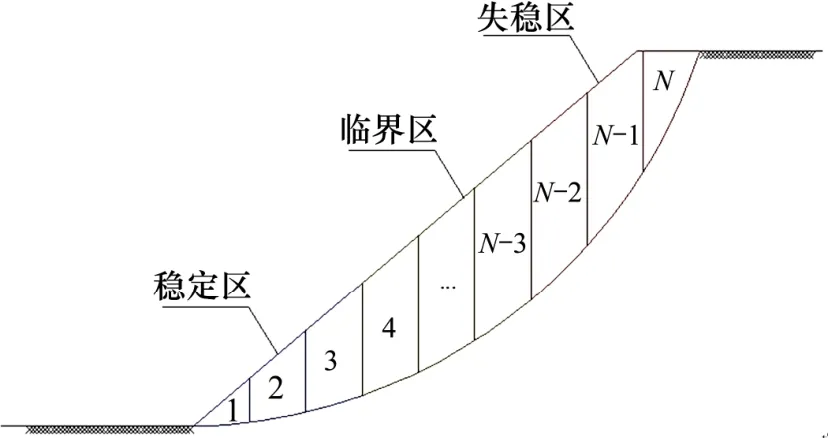
图1 分区计算模型示意Fig.1 Schematic diagram of partition calculation model

准确找到破坏后，按残余强度计算的土体、能抵抗住剩余推力和自身下滑力的土体位置是分区计算模型的关键。模型基于每个条块的力学特点，将边坡土体分为3 个区域：

1) 失稳区。自身的下滑力大于其极限抗剪强度，从而产生局部破坏。

2) 临界区。极限抗剪强度只够抵挡自重产生的下滑力，而无法承受失稳区剩余推力与自身下滑力的双重作用，土体发生局部破坏。

3) 稳定区。极限强度足以承受失稳区的剩余推力和自身下滑力的双重作用，土体稳定。

不对边坡进行处理的情况下，失稳区和临界区就是边坡土体的剪切破坏区。

分区计算模型示意图如图1 所示，自上而下分别为失稳区、临界区、稳定区。但实际工程中，由于边坡的复杂性，可能存在仅有失稳区或稳定区、3 种区域相互穿插等情况。因此，应严格按各条块受力情况和局部安全系数进行分析判断。

2.1 基本假设

分区计算模型按传统条分法竖向条分法进行条块划分，条块底面视为平面。基本假设为：

1) 滑坡是渐进发生的，由某一条块先失稳，之后沿潜在滑移方向，依次影响下一个条块。

2) 各条块潜在破坏模式为沿底面剪切滑动。

3) 每个条块都有自身的安全系数，也称之为条块的局部安全系数。该系数是判断条块分区的重要指标。

4) 条块所受剩余推力的方向与其上一条块的底面平行。

5) 根据力产生的条件，物体之间必须有相互作用，认为：只有上部条块突破极限强度破坏，存在剩余推力的传递，才有条间力的存在。

6) 土体不受拉，条块间不存在拉力。

2.2 求解方法和受力分析

分区计算模型先从边坡最上方的条块N 开始，一直计算到最下方的条块。然后，在该过程中，对各条块进行了完整的力学分析和局部安全系数计算。最后，综合各区域抗剪强度和下滑力，对边坡稳定性作出评价。

模型中，条块受力分析、安全系数计算和力的传递都是在传统条分法的基础上，结合分区计算模型渐进失稳过程中条块的受力特点进行的。

计算过程中，有3 个计算阶段，条块底面存在2 种应力状态：极限应力状态和残余应力状态。为达到各计算阶段预期实现的目的，在满足力学分析的条件下，模型对2 种应力状态进行合理运用，实现对边坡各区域的搜索判定和稳定性分析。具体计算过程为：

1) 阶段一，所有条块不考虑条间力，按极限应力状态计算，求所有条块的局部安全系数fi。fi为极限抗剪强度与剪切力之比。fi＜1 的条块为失稳区条块，这些条块即使没有条块间推力的作用，也会发生自发性的剪切破坏。

2) 阶段二，从边坡顶部条块(受到推力为0)开始，在考虑剩余推力的作用下，按极限应力状态计算局部安全系数fir。当fir＞1 时，判定条块i 属于稳定区，剩余推力以0 向下传递。当fi＞1 且fir＜1 时，判定条块i 为临界区，并按残余应力状态计算其剩余推力向下传递。按滑坡趋势从上至下逐一传递剩余推力，完成每个条块的力学分析和所属区域的判断。

3) 阶段三，基于失稳区、临界区的残余强度和稳定区的峰值强度，计算边坡的安全系数，完成边坡稳定性的评估，并指出基于分区计算模型理论上最佳的支护加固位置。

在这3 个阶段中，值得注意的是：①尽管直接进行阶段二的计算，也能获得渐进破坏下土体的破坏区域，最终边坡安全系数的计算结果一致，但是无法划分失稳区和临界区。利用模型搜索判定失稳区和临界区的理由，除两区域的失稳是否具有自发性外，更重要的是在边坡治理领域中，若采取合理措施，对临界区起点条块的位置进行加固，可抵挡住还未累积过大的剩余推力。此时，由于临界区不受剩余推力作用，不会发生剪切破坏，能继续维持其峰值强度，因此，可经济有效地提高边坡稳定性。②剩余推力加入计算过程中，若无推力产生，则将推力大小以0 传递，提高计算过程的程序化，便于编程计算。③分区计算模型考虑边坡的渐进破坏，主要体现在阶段二对边坡各区域的分析判定中。模型中，从失稳区开始，对破坏土体采取残余应力状态进行计算，获得剩余推力不断向下传递和分析，从而明确基于渐进发展过程中区分边坡各区域界限。

分区计算模型中，极限应力状态下的条块阻滑力，可直接由受力分析和库仑公式求得。而残余应力状态因为剪切面已经出现，则不宜采用极限应力状态继续计算。基于极限应力状态，通过对黏聚力c 和内摩擦角φ 值进行调整，以满足残余应力状态的计算。对于边坡剪切破坏面而言，由于土体性质的差异，黏聚力c 和内摩擦角φ 的衰弱程度[7−9]不同，用衰减系数kc,kφ表示，而衰弱程度的大小主要与土体黏粒含量及塑性指数有关。Skempton[10−11]通过实验证明：当黏粒含量超过50%后，土体残余强度可由黏土矿物之间的摩擦力决定。对于黏土边坡而言，剪切破坏后的残余强度由摩擦力维持，此时可以考虑滑带土黏聚力c 为0(kc=0.0)。

分区计算模型条块的受力如图2 所示。未承受剩余推力的条块受力图如图2(a)所示，有剩余推力传递的条块受力图如图2(b)所示。推力Pi+1可以为0，推力的传递机制与不平衡推力传递系数法相似。因为假设条块沿底面滑移，Pi+1的作用点对该条块局部安全系数和剩余推力的计算没有影响。图2 中，Pi+1作用点并非真实作用点。

图2 条块受力Fig.2 Forces applied on a slice

1) 条块底面的法向力

①未受剩余推力作用，条块的法向力Ni为：

②承受剩余推力作用，条块的法向力Nir为：

式中：Wi为条块重力；αi为条块i 底面与水平面的夹角；Pi+1为上一条块传递下来的剩余推力(若上一条块稳定或自身为最顶端条块则Pi+1=0)；αi+1为上一条块底面与水平面的夹角。

2) 条块下滑力

①未受剩余推力作用，条块的下滑力Qi为：

②承受剩余推力作用，条块的下滑力Qir为：

3) 极限应力状态下的阻滑力

①未受剩余推力作用，条块的阻滑力Ti为：

②承受剩余推力作用，条块的阻滑力Tir为：

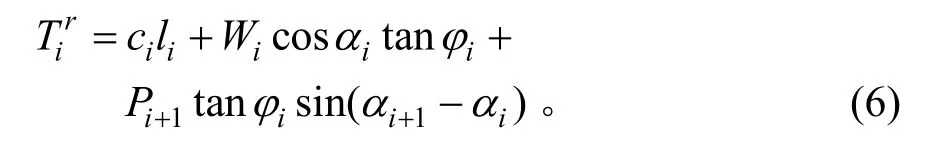
式中：ci为土体黏聚力；li为条块底边长；φi为土体内摩擦角。

4) 残余应力状态下的阻滑力

①未受剩余推力作用，条块的阻滑力Ti'为：

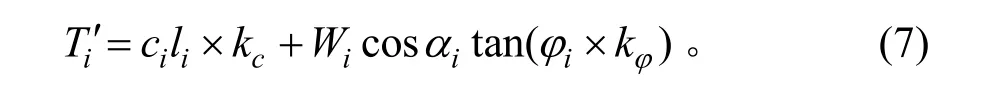
②承受剩余推力作用，条块的阻滑力Tir'为：

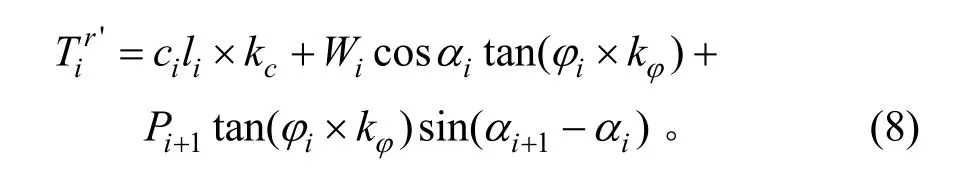
式中：kc,kφ分别为残余应力状态下黏聚力和内摩擦角的衰减系数。

5) 条块的局部安全系数

①未受剩余推力作用，条块的局部安全系数fi：

②承受剩余推力作用，条块的局部安全系数fir：

其中：fi主要用于阶段一寻找失稳区条块；fir主要用于阶段二寻找临界区、稳定区条块。

6) 剩余推力为：

式中：Pi为第i 个条块的剩余推力，考虑土体不存在拉力，故Pi≥0；若计算得到fir＞1，取Pi=0。

7) 边坡安全系数为：

式中： TIi', TC'i为失稳区及临界区条块残余应力状态下的阻滑力；TSi为稳定区条块极限应力状态下的阻滑力；R 为圆弧滑动面半径；K 为边坡安全系数。通过式(1)～(12)依次分析所有条块的受力状态和局部安全系数，完成边坡区域的搜索，并求得边坡安全系数。

2.3 计算步骤

分区计算模型完成滑动面搜索和条块划分后，以条块为基本单元，搜索边坡各区域，并基于各区域不同应力状态计算边坡安全系数。

在整个计算流程中，每个条块需考虑自发破坏的无剩余推力作用和基于渐进破坏[12]的有剩余推力作用进行两次力学分析计算，完成分区后，再求解边坡安全系数，其计算步骤为：

1) 不考虑剩余推力，通过公式(9)，计算出边坡每个条块的局部安全系数fi。

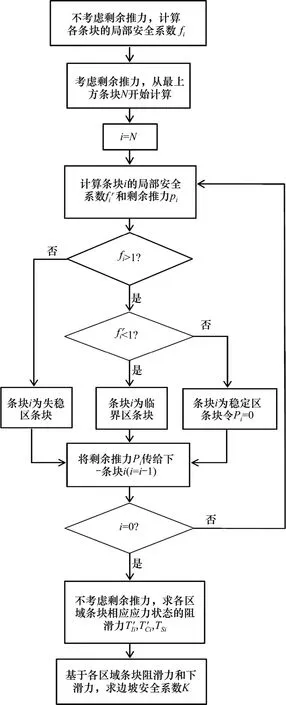
图3 分区计算模型流程Fig.3 Calculation flow chart for partition calculation model

2) 从边坡顶部条块N开始计算，通过公式(10)，(11)，求得其安全系数fNr和剩余推力PN，将PN传递给下一条块N−1，通过相同公式计算其安全系数和剩余推力PN−1。

3) 重复第(2)步中剩余推力的传递及条块的分析计算，直到计算完最底端条块的安全系数f1r。

4) 通过有无剩余推力，求得每个条块的2 种局部安全系数fir和fi的大小，实现对边坡各区域范围的判断。当fi＜1，该条块处于失稳区；当fi＞1 且fir＜1，条块处于临界区；当fi＞1 且fir＞1，条块属于稳定区。

5) 对于不同区域的条块，应采取不同的应力状态来计算其阻滑力。稳定区采取极限应力状态下的阻滑力计算式(5)，临界区和失稳区采取残余应力状态下的阻滑力计算式(7)，采用式(12)计算边坡的安全系数。

3 算例

3.1 程序介绍

为了更好地实现分区计算模型与传统条分法的对比分析，结合滑动面搜索方法及分区计算模型，开发了边坡稳定性分析程序Slope-PCS。该程序设计了交互式的操作界面，采用面向对象的C++作为开发语言，利用微软基础类库MFC，遵守最新的编码规范。程序主要包括文件系统、视图设置、模型绘制、参数设定、分析计算及数据结果可视化6 个模块。

程序设计的计算方法有：瑞典条分法、毕肖普法、不平衡推力法及本研究提出的分区计算模型。通过网格法，实现对滑动面的搜索试算，能较全面地实现边坡的稳定性分析，找到最不利滑面。同时，为保证分区计算模型与其他方法的严格对比分析，程序还设计了指定滑动面的功能，保证了单一变量的原则。

3.2 程序算例分析

本研究提出的分区计算模型，在传统条分法的基础上，考虑了边坡渐进破坏及条块局部稳定性，对各个条块的应力状态做出了力学分析。针对不同应力状态的条块，求解其对应的阻滑力，并基于这种真实应力状态下的阻滑力，计算边坡的安全系数。为了探讨分区计算模型的特点，作者拟采用Slide 软件计算说明书中的工程案例，该黏性土边坡模型如图4 所示，土体容重、黏聚力和内摩擦角分别为20.0 kN·m−3、20.0 kN·m−2、20°。

分别采取瑞典法、毕肖普法及分区计算模型计算，利用自编程序Slope-PCS 进行分析。考虑为黏土边坡，依据Skempton 的实验结论[10−11]，设定残余应力状态下黏聚力c 的衰减系数kc=0，内摩擦角φ 的衰减系数kφ=1，即残余应力状态下黏聚力为0，而内摩擦角不变。

图4 土质边坡模型Fig.4 A soil slope model

本程序中，各传统条分法计算结果与Slide 软件进行对比，验证了程序的正确和计算结果的可靠性。

程序依据瑞典条分法和分区计算模型，得到的结果示意图如图5,6 所示。图6 中，分区计算模型图基于各条块的力学分析和局部安全系数，判断出滑动面各条块的所属区域。工程应用中，可依据该分区标识，进一步进行滑坡治理工作。

由瑞典条分法、毕肖普条分法、分区计算模型计算得到安全系数，分别为：2.039 6,2.124 6,1.461 7。由计算结果可知，对于图4 中的滑动面，分区计算模型的结果较瑞典条分法、毕肖普条分法的偏小。主要是分区计算模型基于边坡渐进破坏，考虑了土体的真实应力状态。上部条块自发性滑移产生剩余推力，并不断累积作用于下一条块，致使坡体某些条块底面的土体发生破坏。这些会产生破坏的土体，按其残余应力状态进行计算。因此，破坏土体的阻滑力采用的是残余强度，分区计算模型的结果可使工程更安全。

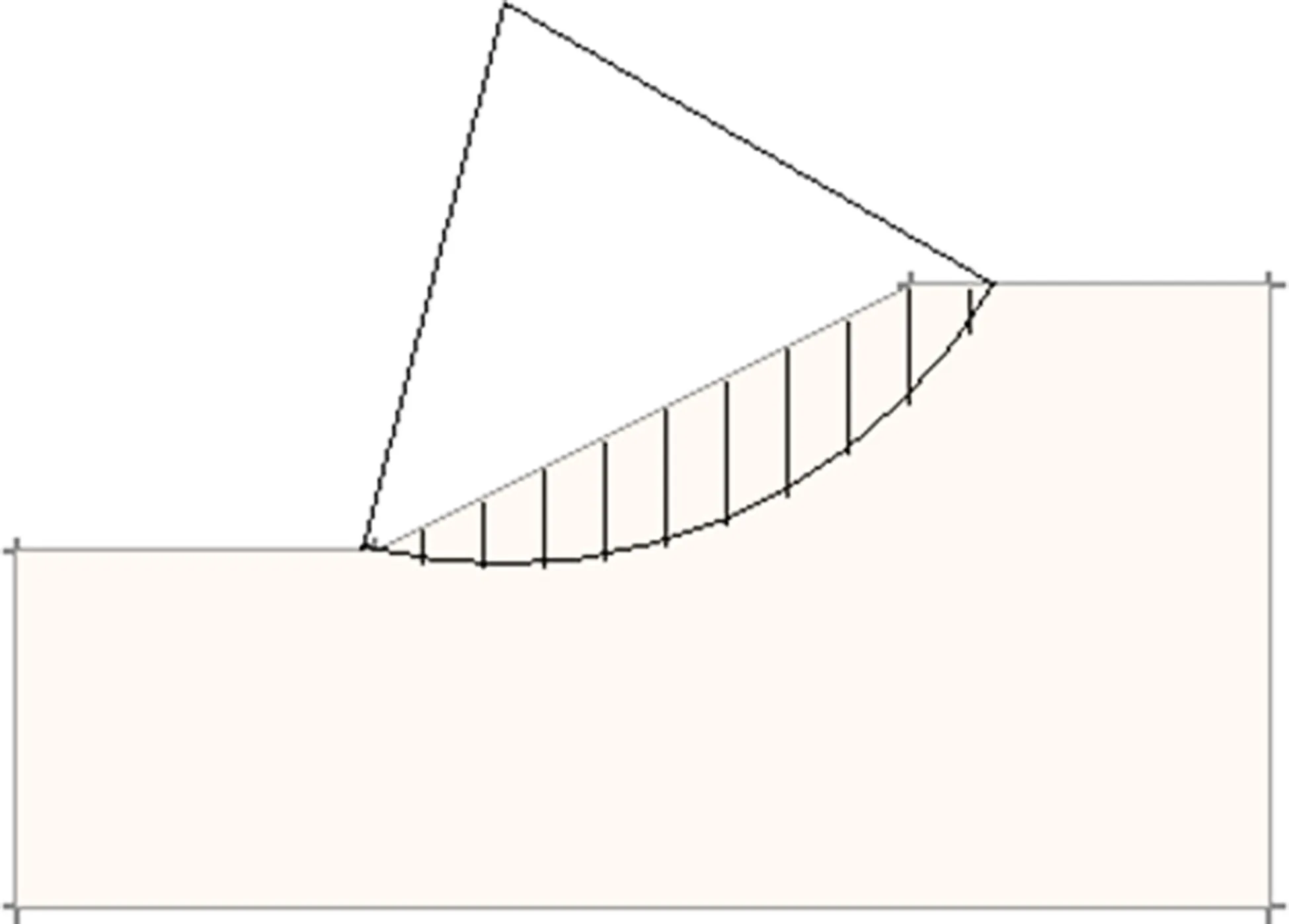
图5 瑞典条分法分析结果Fig.5 Result by Swedish slice method

图6 分区计算模型分析结果Fig.6 Result by partition calculation model

传统条分法安全系数为边坡阻滑力(矩)与下滑力(矩)的比值。其中，阻滑力矩均在极限应力状态下求得，滑面各处皆处于稳定状态。但现实中的边坡往往因为内外部因素的影响，而存在局部失稳区，如：牵引式滑坡[13]、推移式滑坡[14]。所以实际工程中，按照传统条分法分析边坡稳定性，虽然稳定性分析所得安全系数满足要求，但仍可能发生滑坡破坏。

分区计算模型基于边坡的渐进破坏，利用式(9)，(10)求解各条块的2 种局部安全系数，完成对各条块真实应力状态的判断，并以此进行边坡稳定性分析。这是在传统条分法的基础上做出补充和完善，更符合工程实际。

分区计算模型最重要的是对失稳区、临界区及稳定区进行搜索判断，本质是判断边坡各部分土体真实的应力应变状态。由公式(12)可知，与传统条分法的主要区别是阻滑力的计算。其计算结果不仅与土体原始强度参数c,φ 相关，还与残余强度参数、各区域大小有关。根据Skempton 的实验结果，确定黏土边坡残余应力状态下黏聚力衰减为0，而内摩擦角不变。实际工程中，需因地制宜，考虑滑带土残余强度进行计算，发现边坡整体处于稳定区时，分区计算模型的计算结果与瑞典法的相同。

该方法也为边坡治理提供了新思路，有效减少边坡中处于残余应力状态的条块数量，可以大幅度提升边坡稳定性。基于失稳区和临界区发生剪切破坏的特点，在两区域交界处，实施滑带注浆[15]、锚索等支护手段，可以在剩余推力较小时阻断渐进破坏的发展，让临界区条块不受力或少受力，从而转变为稳定区，有效提高坡体稳定性。