基于格林函数的半导体桥三维非稳态传热模型

孙远， 张良， 邓有杞， 李宋， 张淇媛， 张威

(北京大学 信息科学技术学院， 北京 100871)

0 引言

半导体桥(SCB)因具有体积小、发火能量低、作用速度快、可大量同时使用、同步性好[1]等优点，近年来逐渐成为点火器技术的研究热点。SCB的主要工作原理是将电能转化为热能，因此其温度特性对其发火性能有着重要影响。

在对SCB进行热响应分析时所建立的模型可分为集总模型和稳态传热模型。强涛等[3]利用集总模型对器件的安全电流进行了预测，但是该模型比较简单，不能预测桥区温度的非稳态响应，且集总热散失系数对其影响较大，而热散失系数与温度有关，因此通以不同的电流时该模型偏差较大。杨贵丽等[4]通过稳态半球传热模型分析了恒流激励下SCB的能量传递原理以及实验现象，确定熔点是恒流激励时SCB的爆发点，得出了临界发火电流的理论计算公式。但其将圆柱形陶瓷塞简化成半球形以简化边界条件，假设药剂、SCB和陶瓷塞的接触面温度相同，与实际情况相差较大。Lee等[5]建立了稳态传热时SCB的安全电流模型，将桥区视为点热源，因为桥具有低导热性，所以主要考虑热量散失到等效半球形的基底中，但其考虑边界条件时认为基底半径无穷大处温度等于室温，未考虑实际封装尺寸。

由于集总模型和稳态模型不能体现升温速度等结果，本文提出一种基于格林函数的SCB三维非稳态传热模型，对于印刷电路板(PCB)封装的SCB器件，考虑其6个散热面均处于第三类边界条件，利用格林函数求解SCB在恒流激励下的温度响应，并与实验结果对比，具有较好一致性。

1 基于格林函数的三维非稳态传热模型

1.1 格林函数

格林函数法是求解线性热传导问题的经典方法。对于非稳态热传导问题，格林函数描述了非稳态局部热脉冲引起的温度增量。

对于求解线性热传导问题，如本文要讨论的SCB传热问题，格林函数有以下优点[6]：

1)对于长方体PCB封装，每两个对称散热面的边界条件所产生的温度增量相加后抵消，使用温度增量替换温度值可使初始状态产生的温度增量为0，因此只需考虑内部热源即SCB热源产生的影响；

2)PCB的6个散热面具有相同的第三类边界条件，通过建立直角坐标系，可以查找相应的特征函数和特征根；

3)在建立直角坐标系后，可将PCB的3个方向边界条件的一维格林函数相乘，得到整个传热系统的三维格林函数。

1.2 物理模型及基本假设

采用的SCB器件结构如图1所示，电流经铝电极流入SCB桥区并产生焦耳热，桥区向塑封壳、二氧化硅层、硅基底传热至PCB散热板，同时整个器件向空气散热。由于SCB桥区、二氧化硅层、铝电极、硅基底和塑封壳相对于PCB而言太小，尺寸相差2～3个数量级，同时红外测温实验观察到上述小尺寸区域的温度一致，温降主要发生在PCB区域，因此忽略桥区、二氧化硅层、铝电极、硅基底以及塑封壳的传热过程，将散热视作由PCB完成。建立直角坐标系如图2所示，其中：z轴为厚度方向，x轴为长度方向，y轴为宽度方向，H为PCB在z轴方向的长度即厚度；W为PCB在y轴方向的长度即宽度；L为PCB在x轴方向的长度即长度；L1为热源在x轴方向的下边界；L2为热源在x轴方向的上边界；W1为热源在y轴方向的下边界；W2为热源在y轴方向的上边界；H1为热源在z轴方向的下边界；H2为热源在z轴方向的上边界。为了简化边界条件，将桥区因焦耳定律产生的热量视为由一个长方体均匀热源产生，该长方体热源位于PCB内部靠近表面处，与PCB共用z=0 mm平面，即图2模型示意图中的红色部分。

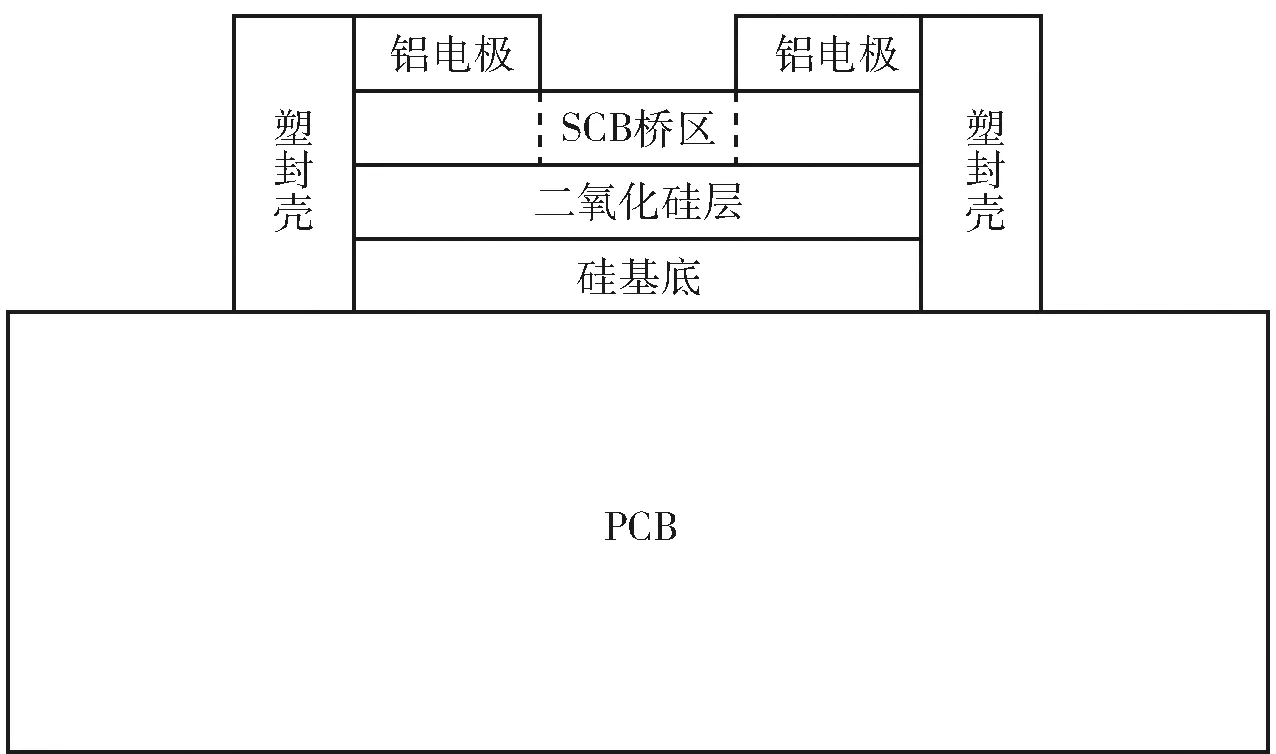
图1 SCB器件结构示意图Fig.1 Structure of semiconductor bridge device

图2 模型示意图Fig.2 Model

由于PCB体积相对于SCB特别大，边界条件只考虑PCB与空气的对流散热，共归纳为4条基本假设。

1)将热源部分简化为长方体，热流密度q=I2R/V，其中V为长方体体积，I和R分别为电流和电阻；

2)PCB所有界面均处于第三类对流散热边界条件；

3)仅考虑热传导一种传热方式，忽略其他传热方式，例如热辐射；

4)传热过程中PCB的导热系数、密度、比热容等均不随温度变化。

1.3 求解过程及结果

在图2坐标系下建立方程(1)式～(5)式，其中：(1)式为PCB模型的热传导方程；(2)式～(4)式为PCB 3个方向上的边界条件；(5)式为初始温度条件。

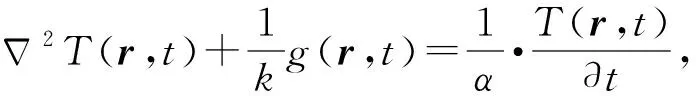
(1)

(2)

(3)

(4)

T(r,t)=T0,t=0.

(5)

令ΔT=T-T0，进行变量替换，最终只需将温度增量ΔT加上初始温度T0，即可得到实际温度。引入格林函数对模型进行计算，则上述公式转变为以下形式：

(6)

(7)

(8)

(9)

G(r,t|r′,τ)=0,t<τ.

(10)

式中：G为格林函数；δ为冲激函数；r′为热源处的空间三维坐标；τ为r′处热源产生热量的时刻。类似地，(6)式为该模型格林函数形式的热传导方程，(7)式～(9)式为边界条件，(10)式为初始条件。根据格林函数推导过程，最终温度分为3个部分产生影响的和[6]：

T(r,t)=ΔTi(r,t)+ΔTg(r,t)+ΔTb(r,t)，

(11)

式中：ΔTi(r,t)为初始温度的影响；ΔTg(r,t)为内部热源的影响；ΔTb(r,t)为边界条件的影响。对于等号右边第1项，由于已经使用ΔT=T-T0进行了变量替换，相当于使初始温度等于0 ℃，因此ΔTi(r,t)为0 ℃；对于第3项，由于所有边界条件均为第三类边界条件，同一方向上两侧边界条件的影响相加后抵消，因此ΔTb(r,t)也为0 ℃. 从而这个模型的最终温度增量仅需考虑内部桥区长方体热源的影响，即

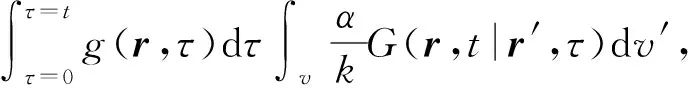
(12)

式中：v表示整个体积；v′表示体积微分元。

对于直角坐标系，(12)式中的r可替换为x、y、z且对3个坐标轴方向分别进行积分后再相乘，即

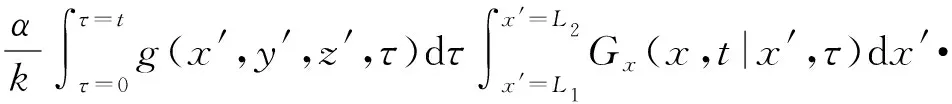
(13)

式中：x′、y′、z′为热源坐标；(x′,t|x′,τ)为τ时刻x′处的点热源对t时刻x处温度产生的影响，(y′,t|y′,τ)、(z′,t|z′,τ)类似；Gx为x轴方向的格林函数；Gy为y轴方向的格林函数；Gz为z轴方向的格林函数。由(13)式可分别获得3个坐标轴方向的格林函数方程，根据理论计算与总结可得到这些方程的解[6]。由于所有边界条件均为第三类边界条件，因此计算过程类似。例如在x轴方向上，当x=0 mm和x=L时，均处于第三类边界条件，此时x轴方向的格林函数解为

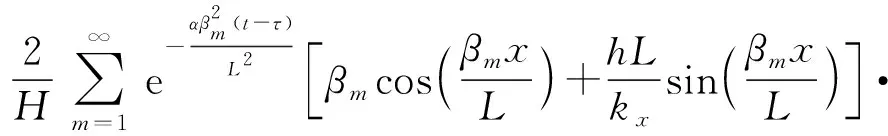
(14)

式中：m为特征根序号；kx为x轴方向的热传导系数；特征根βm为以下超越方程的根，

(15)

同样，y轴和z轴方向的解也有类似形式，不一一写出。

考虑硅的电阻率会随着温度升高产生变化，最终影响焦耳效应的产热量，由假设(1)式，长方体热源的单位体积热功率为

(16)

式中：R0为初始电阻；a为温度系数；ΔT为温度增量。由(16)式可以看出，单位体积热功率q可以分为两部分，其中：第1项I2R0/V为常数，代表由初始电阻产生的热量；第2项与温度增量ΔT有关，设T0为初始电阻产生的温度增量，该部分温度增量造成的电阻变化产生的温度增量为T1，最终温度增量为这两部分的和，即最终温度增量为

ΔT(x,y,z,t)=T0(x,y,z,t)+T1(x,y,z,t)，

(17)

式中：

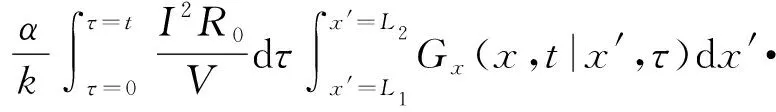
(18)

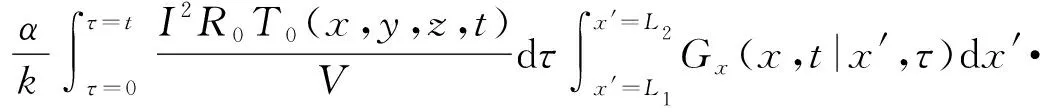
(19)

事实上，温度增量T1造成的电阻变化进而可以导致温度增量T2，T2造成的电阻变化进而可以导致温度增量T3，依此类推。这里为简化计算，只考虑初始电阻对温度增量造成的影响即T0和T1，最终结果与实验数据较为符合。联立(12)式～(19)式，可获得SCB在不同时刻的温度增量。本文使用计算软件Maple联立公式并得出温度值。模型中涉及到的关键参数取值如表1所示。

表1 关键参数取值

因为PCB板在x轴、y轴、z轴方向的热传导系数不一致，因此在计算热扩散系数α时，使用导热系数的几何平均值k[10]，即k=(kxkykz)1/3,则α=(kxkykz)1/3/(ρc)。

最后所得温度应为在x轴、y轴、z轴方向上特征根的无限求和，经过实际计算，当m取值到4时，最终温度的变化不再大范围波动，因此在此次求解过程中求和至m=4，经过Maple软件计算，x轴、y轴、z轴方向上的前4个特征根取值如表2所示，结果取3位有效小数，其中γm为y轴方向的特征根；λm为z轴方向的特征根。

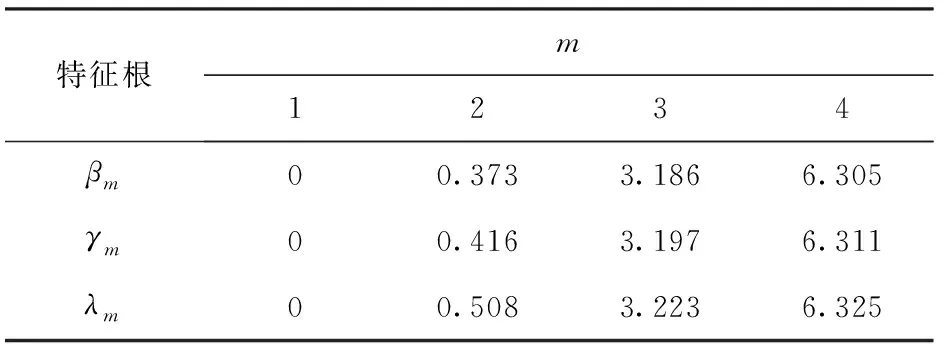
表2 特征根取值

最终解出在不同电流激励下，SCB的最高温度随时间变化如图3所示。取模型桥区表面中点即(L1/2+L2/2,W1/2+W2/2,0 mm)处为温度最高点位置。

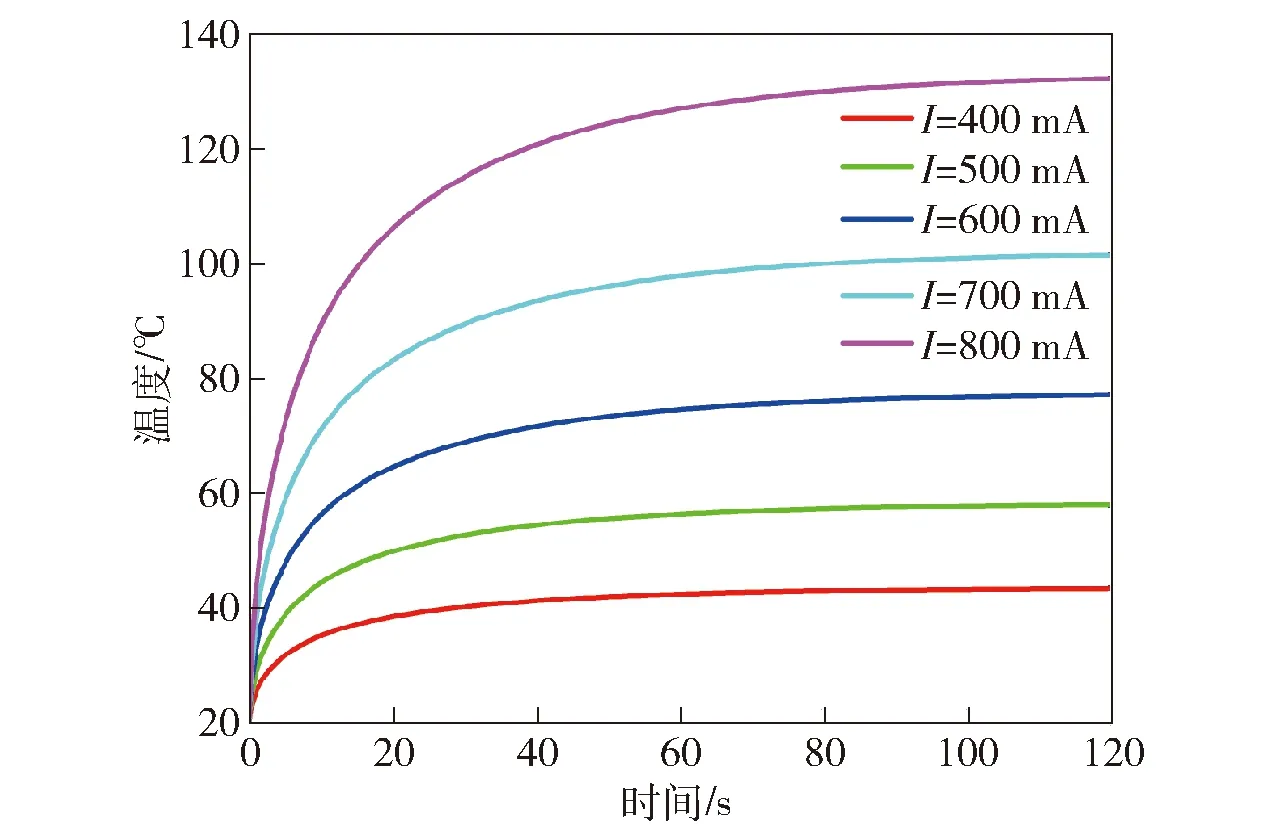
图3 不同电流下的温度变化图(模型计算值)Fig.3 Change in temperatures at different currents (calculated values)

由图3可知，在不同电流激励下，SCB在60 s时温度趋于稳定。

输入电流为800 mA，时间为120 s时，z=0 mm界面上的温度分布如图4所示。

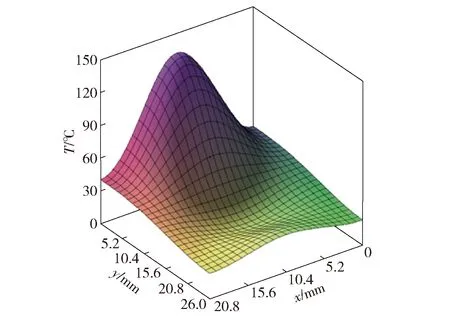
图4 表面温度分布图Fig.4 Surface temperature distribution

由图4可以看出：时间为120 s时，在z=0 mm界面上，温度在桥区表面中心处温度最高；在桥区之外，随着PCB向边界传热以及从表面向空气对流散热，温度逐渐降低。温度出现凹坑区域是由格林函数的累加特性导致的，无法避免。图4较为符合实际情况，进一步说明了本文模型的正确性。

2 红外摄像仪实验结果对比

2.1 实验方法

红外摄像仪是一种测量物体发出的红外辐射从而检测温度的装置[11]。测温时将红外摄像仪对准SCB，然后设定恒流源电流大小，并在分析软件中设定触发条件。由于室温为20 ℃，设置触发温度为25 ℃. 当记录时间到达150 s时，桥区温度基本不变，桥区电阻不再变化，此时结束录制。在对SCB通电的同时开始记录升温过程，同时用电压表测量SCB的电压。记录数据时由于发热部位主要在桥区，因此选取桥区作为主要研究对象，并选择记录最高温度模式，在软件中观察到记录点位于桥区中心,即桥区中心处温度最高。分析温度区间设置为0～500 ℃，测温实验共采用5支样品。

2.2 实验设备及校准

本文采用的红外摄像仪由北京理工大学提供，按照国家计量技术规范JJF 1187—2008热像仪校准规范进行示值误差和测温一致性校准，其中测温一致性实验测温点分布如图5所示。

红外摄像仪型号为美国FLIR SYSTEM公司生产的Thermo Vision SC300-Series，并加配一个22 mm的显微镜头，以便对微米尺寸的SCB进行测量。使用配套的分析软件，直接实时地对温度进行记录并分析。实验装置示意图如图6所示。

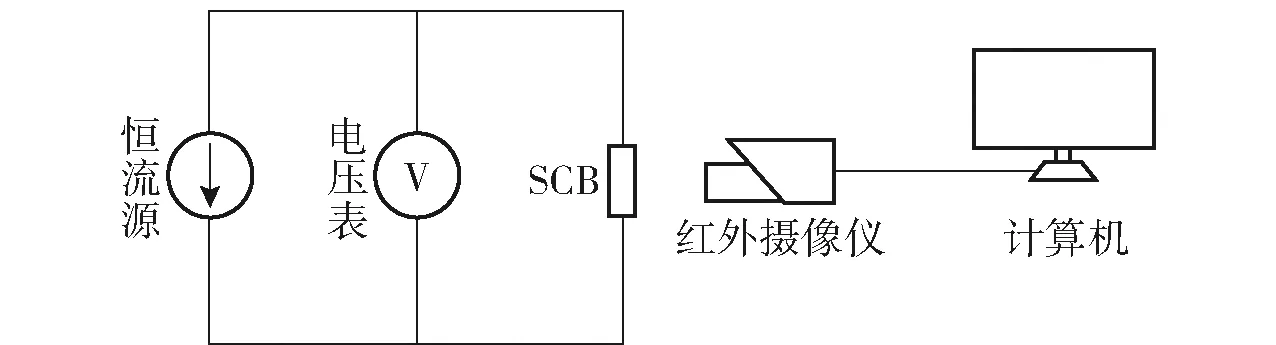
图6 实验装置示意图Fig.6 Experimental equipment

2.3 实验结果

以样品1为例，在400 mA、500 mA、600 mA、700 mA、800 mA的恒流激励下，样品的最高温度随时间变化如图7所示，实验时发现最高温度出现在桥区表面中心区域。

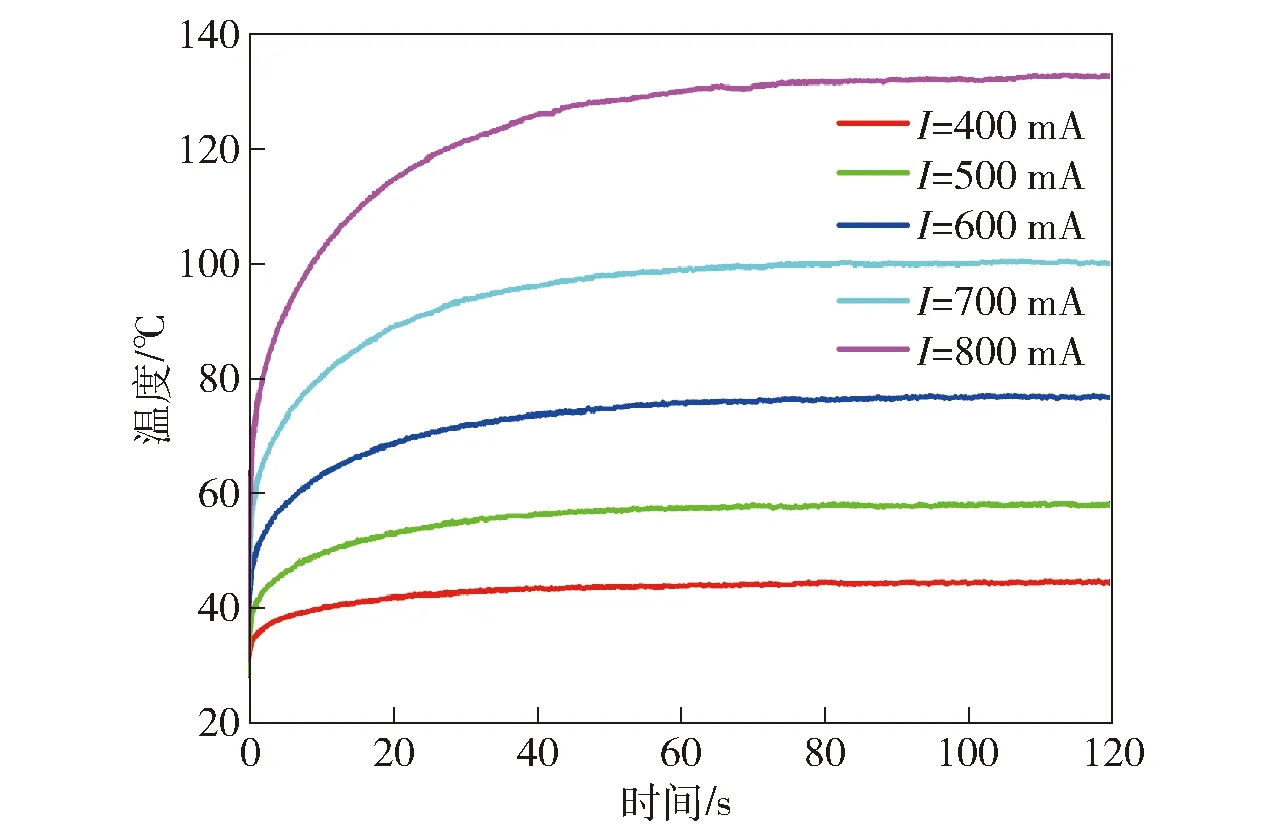
图7 样品1在不同电流下的最高温度变化图(实验值)Fig.7 Change in temperatures at different currents (experimental values)

由图7可见：桥区的最高温度随着电流激励的增大而增大，因为在这段时间内，电流通过SCB产生的焦耳热大于SCB通过自身和PCB板向空气散失的热量；60 s左右，电流产生的热量与散失的热量达到动态平衡，最后温度稳定在最高温度，不再增加；当电流激励增大时，热动态平衡所需的时间更长。

同样地，其余4支样品具有相同的变化趋势，其最高温度如表3所示。

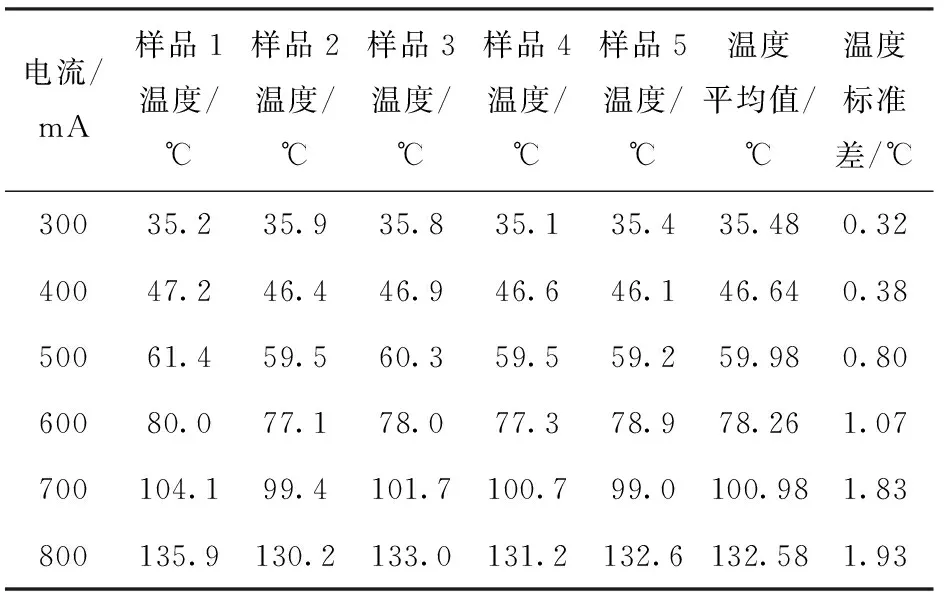
表3 不同样品在不同电流激励下的最高温度

从表3中的标准差可以看出，随着电流的增加，SCB的最高温度偏差增大，因此在大电流激励下，样品最高温度的差异性更明显。这是因为每个SCB的工艺加工环境不完全相同，导致其电阻温度系数不同，在大电流下，积聚热量越多，其温度系数造成的温度变化更明显。

2.4 理论模型与实验数据对比

选取样品1且施加电流为800 mA的典型情况，对施加相同电流时的模型仿真温度变化曲线与实验温度响应曲线进行对比分析，结果如图8所示。

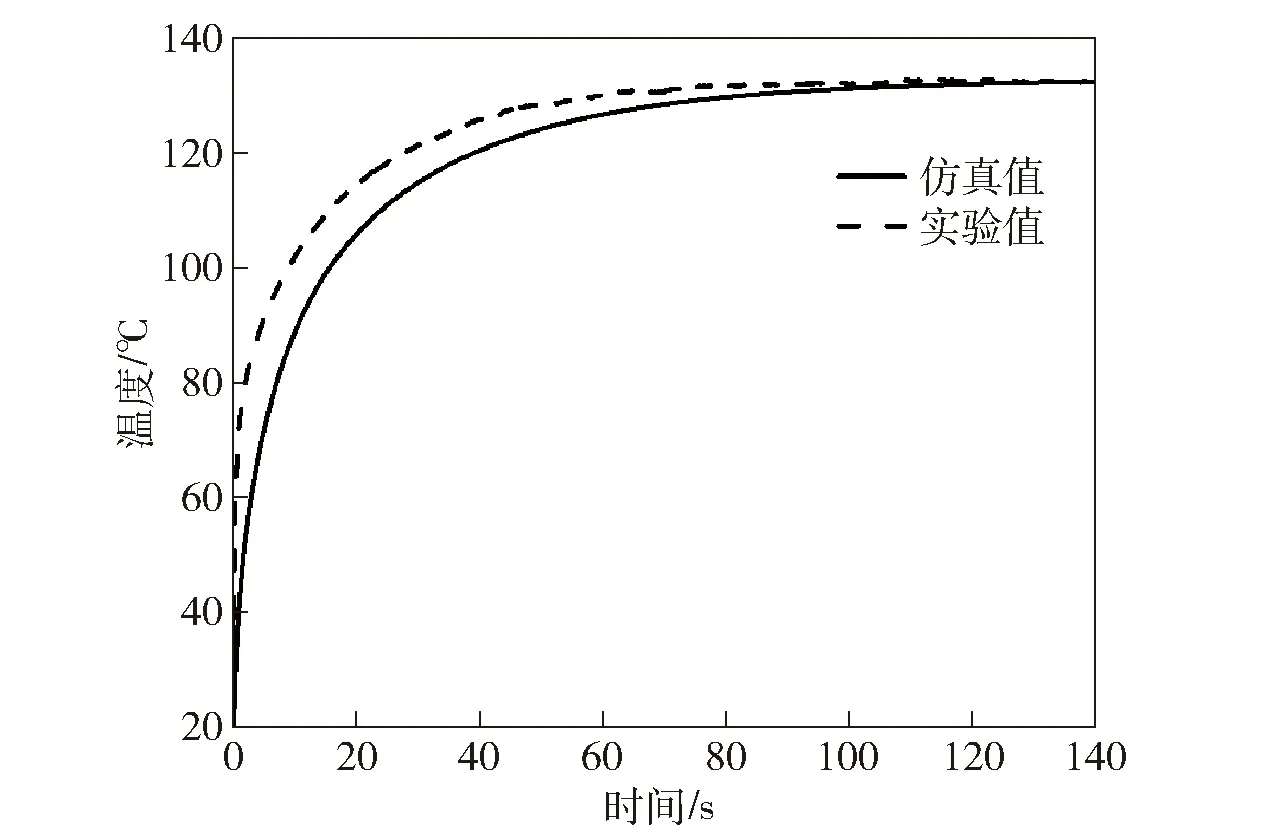
图8 温度仿真值与实验值对比Fig.8 Comparison between simulated and experimental temperatures

由图8中两条曲线对比可知，仿真与实验的温度变化趋势一致，在60 s后温度都基本稳定，但是实验值始终大于仿真值，尤其在初始阶段的相对误差较大。分析原因有：该模型将热源置于PCB内部，相当于等效加强了SCB与PCB的传热效果，实际上SCB附着在PCB表面，从桥区热源传热到PCB存在延迟，因为红外测量的最高温度是桥区表面温度，所以会使得实际升温速度始终略高于模型；实验时由于红外摄像仪自身发热，测量低温时，红外传感器接收到镜头部分的红外辐射，导致测量得到的温度略高于桥区的实际温度，对后续传热过程也有影响，但随着桥区温度的升高，这部分影响逐渐减小至忽略不计。

将施加不同电流时实验的最高温度与仿真的最高温度进行对比分析，如表4所示。

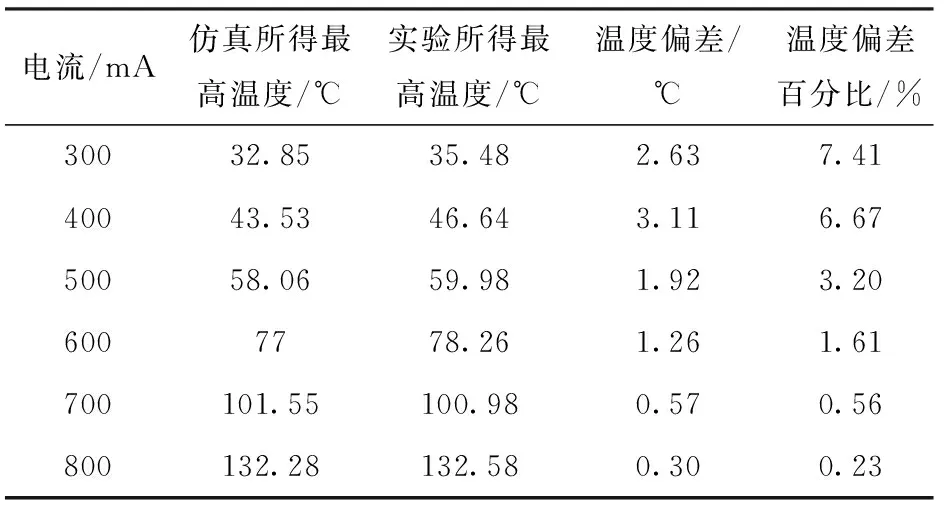
表4 对比模型与实验在不同电流下的最高温度

由表4可见，模型仿真所得最高温度与实验最高温度的最大温度差不超过4 ℃，在300 mA时偏差百分比最大，随着电流的增大，温度偏差百分比越来越小，这与红外摄像仪的测温原理有关：红外摄像仪由传感器从镜头接受物体的红外辐射后进行信号处理得到温度，在桥区表面温度较低时，红外摄像仪的自身发热使得镜头温度升高，最终传感器接收到的红外辐射中，镜头部分的影响不可忽略，使得最终的测量值偏高，当桥区表面温度升高时，镜头部分的影响迅速减小，因此该非稳态传热模型对于预测在较大电流下的温度变化更为准确。

3 结论

对于PCB封装的SCB传热问题，本文将格林函数法应用于建模过程，提出一种SCB三维非稳态传热模型。进行了SCB测温实验，将模型计算结果与实验数据进行对比后较为一致，验证了该传热模型的准确性。针对长方体形的PCB封装，使用格林函数法能考虑全部6个散热面的边界条件，与半球模型忽略SCB一侧散热平面且将圆柱形陶瓷塞外壳近似为半球形的边界条件相比，更为接近真实情况。针对PCB封装SCB的安全电流要求，可使用该模型分析传热情况，并结合使用药剂的热分解温度等，对设计起到参考作用。