基于磁热流多场耦合的双沟四回路电缆温度场分布与载流量计算
2020-02-05刘刚许志锋王鹏宇黄世杰贺德辰黄展鸿洪圣泽
刘刚 许志锋 王鹏宇 黄世杰 贺德辰 黄展鸿 洪圣泽
(华南理工大学 电力学院,广东 广州 510640)
随着我国输配电网改造工作的实施,城乡输电线路的电缆化率不断提高[1- 4]。电缆沟作为电缆地下敷设方式的一种,具有容纳线路数量多、便于运维检修等优点,在电力线路走廊建设中得到了广泛应用[5- 7]。
双沟敷设多回路电缆是一种特殊的高压电缆集群敷设方案。采用这种敷设方案时,受多回路电缆相互间电磁和散热的影响,沟内不同位置的散热条件可能存在较大差异。位于不利散热位置的电缆如果长期工作在重载情况,则可能造成绝缘劣化,缩短其预期使用寿命[8- 10]。因此,研究双沟敷设多回路电缆的温度分布特点,准确核算不同回路电缆的载流能力,对于保证沟内电缆群的安全运行具有重要意义。
IEC60287作为目前使用最为广泛的电缆载流量评估方法,提供了直埋、排管等多种典型安装方式下电缆载流量的计算公式。然而该标准方法建立在多种假设条件之上,在计算非常规敷设条件下的电缆载流量时误差较大[11- 12],并且此标准中并未涵盖双沟敷设多回路电缆的载流量评估方法[13- 14]。随着计算机技术的快速发展,数值计算方法在复杂敷设环境下的电缆载流量评估中得到了越来越广泛的应用[15- 17]。文献[18- 20]建立了单一温度场仿真模型,并分析了多种不同影响因素作用下沟内敷设电缆的载流量变化;文献[21]利用涡量-流函数模拟沟内空气自然对流,并使用迭代法求解热流耦合效应,计算了沟槽敷设单根电缆时的温度场及流体场分布;文献[22- 23]建立了热流耦合模型,分别分析了电缆沟几何因素以及通风风速对沟内电缆载流量的影响;文献[24]建立了磁-热-流多场耦合模型,分析了多回路电缆同沟敷设时在规则和不规则放置情况下的载流量变化。由以上分析可知,现有对沟槽敷设电缆载流量的相关研究中,同时考虑了磁-热-流三场耦合作用的较少,且目前缺少对于双沟敷设多回路电缆的温度场分布和载流量影响因素的研究。
针对以上问题,本文构建了基于磁热流多物理场耦合的双沟敷设四回路电缆有限元仿真模型,分析了电缆沟宽度、中间沟壁厚度和回填沙土对沟内不同回路电缆稳态温度分布以及载流量的影响,并进一步提出了双沟四回路电缆的优化敷设方案。
1 多物理场耦合模型的构建
1.1 建模假设
双沟敷设多回路电缆的磁-热-流耦合作用直接影响电缆的产热和散热,因此构建的模型中需要同时考虑电磁场、温度场和流体场(未回填沙土时)。为了减少模型计算量,建模时进行以下简化:①假设沟内电缆无限长,不考虑轴向传热的影响,将三维模型等效为二维模型,同时忽略沟内电缆支架的影响;②导体焦耳损耗是电缆的主要热源,模型中忽略介质损耗以及金属护套损耗的影响;③未回填沙土情况下,电缆沟内存在的封闭空气域自然对流速度较低,可认为沟内空气为不可压缩流体,采用Boussinesq近似。
1.2 物理场设置
本文采用COMSOL有限元仿真软件中的非等温流动模块建立温度场和流体场,分析沟内电缆热流耦合的影响;通过添加面对面辐射模块模拟电缆的辐射传热,并利用Hemicube方法计算辐射角系数,从而模拟沟内电缆的热传导、热对流、热辐射3种传热方式。
模型中采用电磁热源,并设置导体电导率为温度的函数,将耦合模型中温度因变量引入,作为导体工作温度T,从而建立模型中导体电导率与运行温度的关系。铜导体的电导率σ与温度的函数为[24]
(1)
式中:T为导体工作温度,K;Tref为导体初始参考温度,K;ρref为导体在初始温度下的参考电阻率,Ω·m;αCu为铜导体电阻率温度系数,K-1。
1.3 边界条件
电缆沟外部土壤环境可以分别采用3类边界条件[25],如下所示。
第Ⅰ类:
T(x,y)|Γ=f(x,y)|Γ
(2)
第Ⅱ类:
(3)
第Ⅲ类:
(4)
式中:x、y为二维几何模型中的坐标位置;n为边界外法线方向;Γ为区域边界;T为温度,K;Tf为外界环境温度,K;k为介质导热系数,W/(m·K);q为热流密度,W/m2;h为表层空气的对流换热系数,W/(m2·K)。
根据电缆沟实际敷设环境的边界特性,对位于电缆沟模型下侧的深层土壤可以采用第Ⅰ类边界条件,模型中深层土壤温度为15 ℃;对电缆沟两侧土壤边界采用第Ⅱ类边界条件,取法向热流密度q为0 W/m2;对地表可以采用第Ⅲ类边界条件,对流换热系数为12.5 W/(m2·K)[7],取外界空气温度为20 ℃。
对于电缆外表面以及电缆沟内壁等流固边界,根据流体力学相关理论,由于粘性力的作用,附着在其表面的空气相对速度为零。因此,在模型中将其设置为无滑移壁,作为沟内封闭空气层的流体场边界条件,对应的边界方程为[7,21]
u=v=0
(5)
式中,u、v分别为水平和竖直方向上的空气流速,m/s。
1.4 模型验证
为验证本文构建的基于磁热流多物理场耦合模型的正确性,本文利用文献[2]中搭建的电缆沟敷设电缆温升试验进行对比验证。根据本文提出的方法,保持物理场、边界条件等相关设置条件一致,并根据文献中试验现场实际条件调整环境参数,建立了与温升试验现场对应的仿真模型。对比结果显示,800 A和1 200 A负载情况下,本文构建模型的误差分别为1.1%与3.8%,均满足工程需要,初步验证了多场耦合模型的有效性。
1.5 计算实例
双沟四回路敷设电缆典型设计方案中的几何模型如图1所示,其左右电缆沟宽度L1为1 200 mm,中间沟壁厚度L2为260 mm,每侧电缆沟各敷设两回路电缆,从左至右分别标记为回路1至回路4。沟内电缆型号为64/110 kV YJLW02 630 mm2电缆,其结构参数如表1所示,仿真模型中其他相关环境参数设置如表2所示[7,25- 26]。
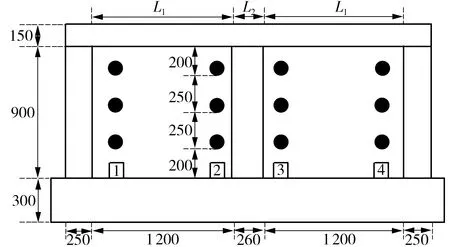
图1 双沟四回路电缆沟的几何示意图(单位:mm)

表1 仿真电缆结构参数Table 1 Structure parameters of the cable in model
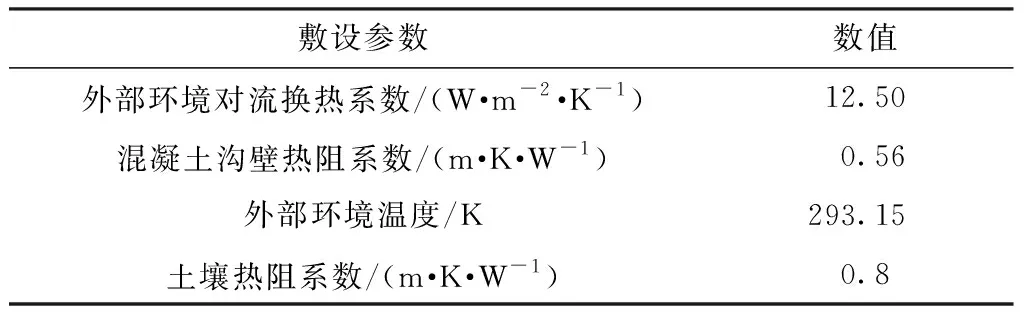
表2 仿真模型相关参数Table 2 Relative parameters of the model
基于上述模型,对沟内电缆加载相同负载。当负载电流为1 012 A时,电缆沟温度场和流体场的分布分别如图2、3所示。由图2可知,稳态时沟内电缆最高导体温度为90.04 ℃,此时加载的负载电流已达到电缆载流量限值。图3为电缆沟内对应的空气流速分布图,图中箭头代表空气流动速度矢量,箭头大小与空气流速成正比。由图3可知,受电缆与电缆间、电缆与电缆沟壁之间相对位置的影响,沟内空气流速并不均匀,流速最大为0.17 m/s,最小接近0 m/s。由对流换热计算公式可知[27],空气流速的差异造成沟内不同位置电缆的对流换热效果存在差异,影响了沟内温度场分布。若使用对流换热系数等效电缆沟内封闭空气层对流换热影响可能会造成较大误差。

图2 双沟四回路电缆温度场分布
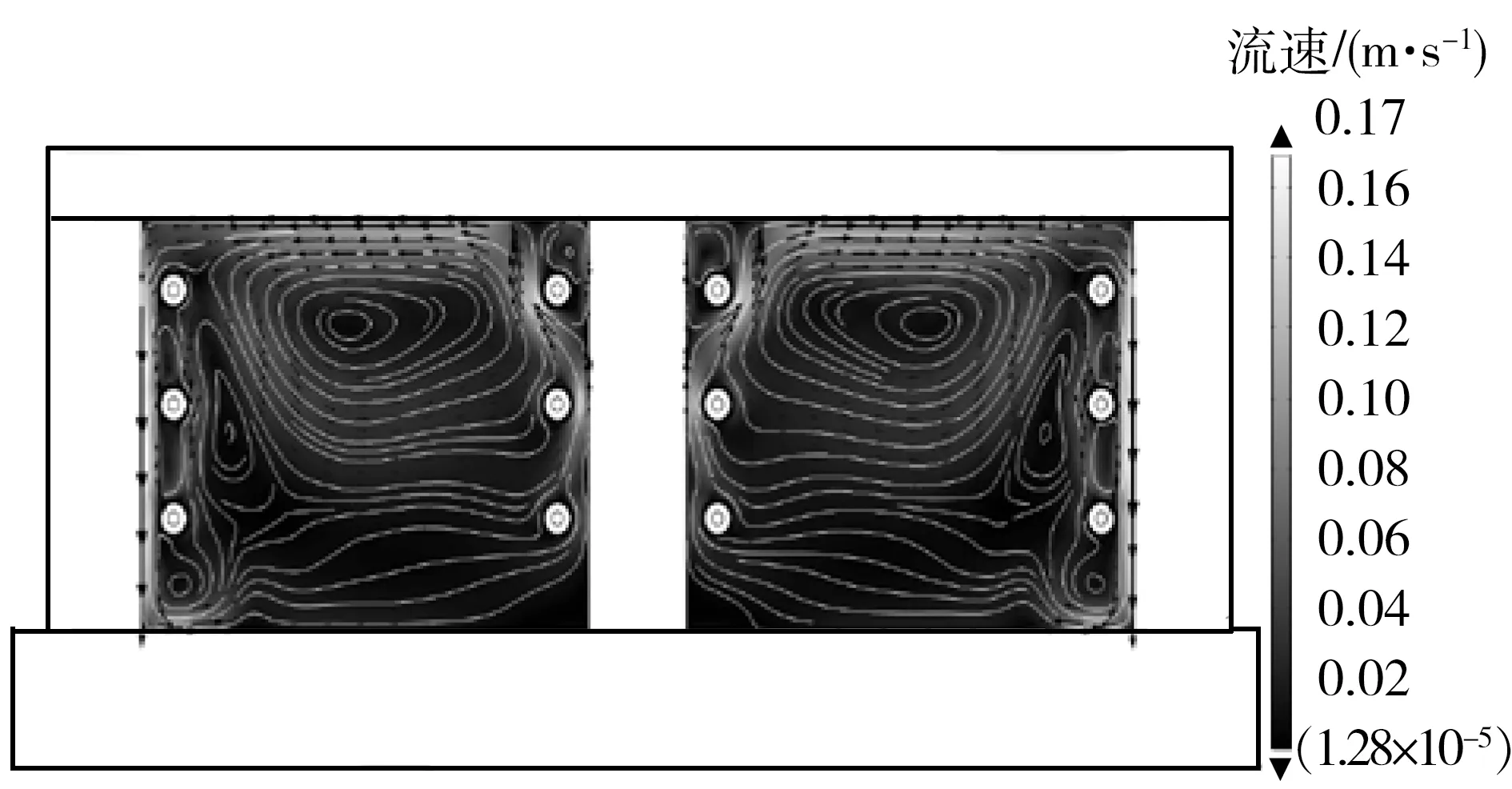
图3 电缆沟内流速分布图Fig.3 Flow velocity distribution of cable trench
进一步分析沟内四回路电缆的稳态导体温度差异,结果如表3所示。由表3中数据可以发现,负荷相同情况下,对于同一回路内的电缆而言,位于中间相的电缆导体温度较高。对于不同回路电缆,回路1和回路4、回路2和回路3的温度基本相等,左右两侧电缆沟内的电缆导体温度呈对称分布,因此分析双沟任意一侧电缆沟内的电缆温度分布即可。以左侧电缆沟为例,受另一侧电缆回路散热的影响,靠近双沟中间壁的回路2的三相电缆导体温度均高于靠近同侧电缆沟的电缆回路1,两者平均温度相差2.64 ℃,导体温度相差最高达5.16 ℃。对于采用双沟四回路敷设方案的电缆,相同条件下靠近中间沟壁的两回路电缆发热更严重,该位置是这种敷设方案下电缆载流量的瓶颈位置。
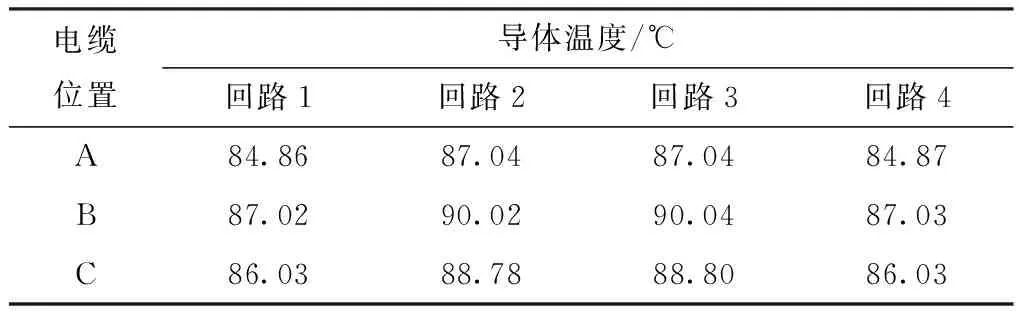
表3 双沟四回路电缆的导体温度
2 双沟四回路电缆载流量影响因素分析
由前述可知,相比常规的电缆沟设计方案,双沟敷设电缆载流能力的核算需要额外考虑中间侧回路电缆的温升。分析电缆沟几何设计因素对双沟敷设电缆温度分布的影响,对于确定沟内多回路电缆的载流能力具有重要意义。
2.1 电缆沟宽度L1的影响
电缆沟宽度决定了电缆回路之间的距离,直接影响了电缆的散热条件。本文在前述构建的仿真模型基础上,将电缆沟宽度作为单一变量,分析电缆回路最高导体温度和对应载流量的变化。同样以左侧电缆沟为例进行分析,回路1和回路2的计算结果如图4所示。
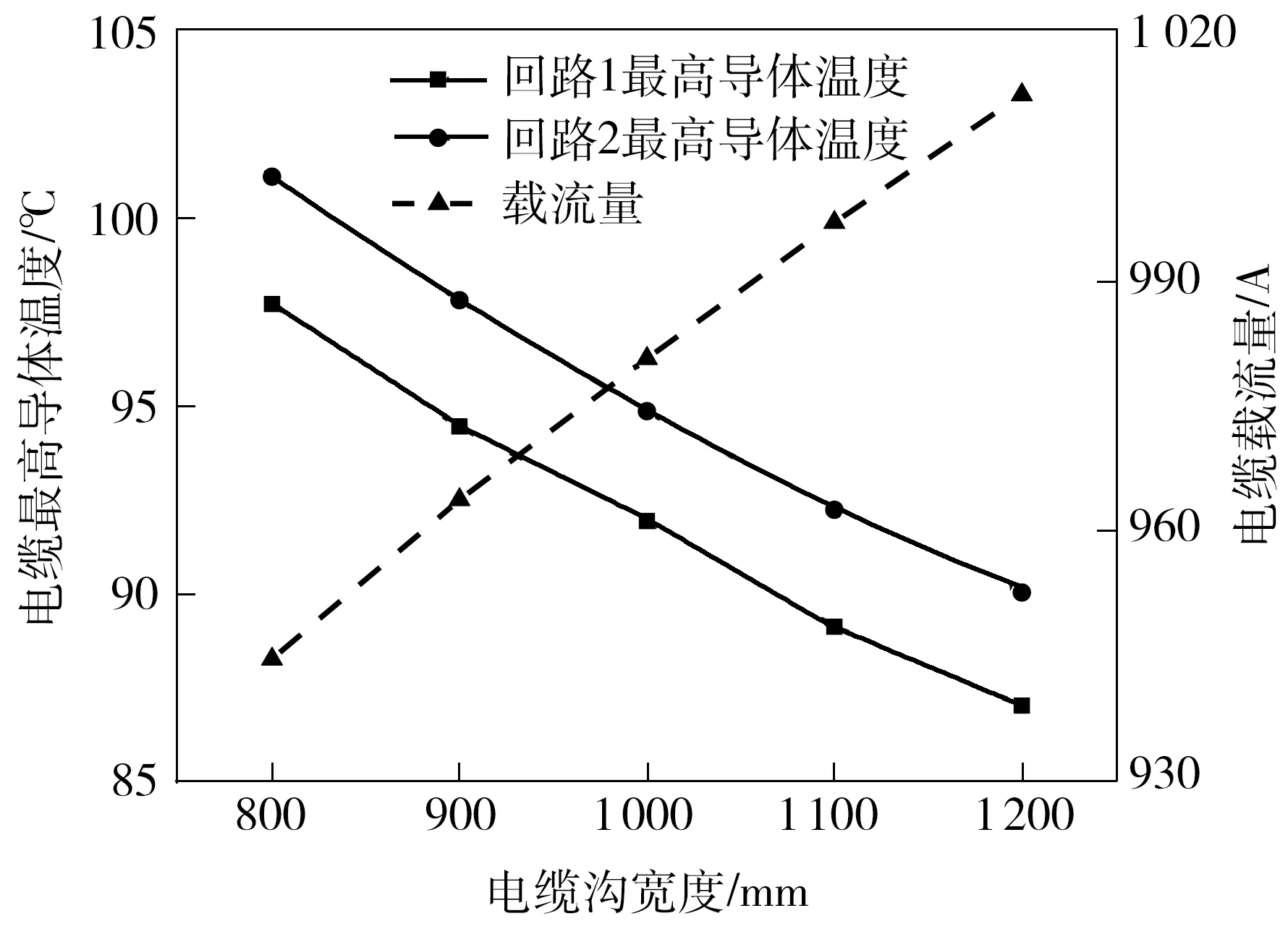
图4 电缆沟宽度对电缆导体温度与载流量的影响
分析图4可得,负载电流保持不变,当电缆沟宽度从1 200 mm减小到800 mm时,沟内两回路电缆的最高导体温度近似呈线性增长,两回路电缆的最高导体温度均升高了约10 ℃,且靠近中间沟壁的回路2的温度整体比回路1高了约3 ℃。随电缆沟宽度从1 200 mm减小到800 mm,回路2电缆的载流量从1 012 A减小到945 A。
电缆沟宽度的减小一方面减小了沟内封闭空气域的对流空间,造成电缆沟内空气温升增加,使电缆的散热环境恶化;另一方面,电缆沟宽度的减小实际上减小了电缆回路的间距。电缆作为热源,其发热量与导体交流电阻大小密切相关,间距的减小加强了沟内电缆之间的互热效应与邻近效应[28- 29]。根据电缆导体交流电阻的计算公式[13],温度和邻近效应系数增大均会导致交流电阻升高,使电缆产热增加。这两方面原因造成沟内电缆温升增加、载流量下降。由于回路2与回路3间距更近,电缆间的互热效应与邻近效应更强,因此其稳态温升更高。
2.2 回填沙土的影响
考虑到电缆沟的防火需求,常常会采用回填细河沙的施工方案。本文在前述构建的双沟敷设电缆模型基础之上,将电缆沟内空气层部分替换为回填细沙,并删除流体场及相关的传热模块,其余设置不变,研究沟内回填细沙对双沟敷设四回路电缆的稳态导体温度及载流量的影响。


表4 不同回填情况下电缆回路的最高导体温度及载流量
回路1和回路2在不同工况下温升差异的原因在于:电缆沟未回填沙土时,热对流和热辐射是沟内电缆主要的传热方式,并且产生的热量主要通过顶部盖板传递到外界[21,32]。电缆沟内回填沙土时,沟内电缆通过热传导传递到周围的环境。由前述分析可知,由于回路2更靠近另一侧电缆沟内的回路3,因此这两回路电缆具有较强的互热效应[29,33]。当回填沙土热阻系数较小时,回路2和回路3产生的热量在更容易传递到周围细沙的同时,两回路之间散热的影响也会加强;当回填沙土热阻系数较大时,两回路的不利散热影响叠加,造成局部温度上升幅度更大,因此呈现出与回路1不同的变化特点。
进一步分析中间沟壁厚度L2变化时双沟敷设电缆最高导体温度变化,结果如图5所示。未回填细沙情况下,当中间沟壁厚度从260 mm减小到140 mm时,由于沟内空气区域大小并未改变(电缆热量仍然主要通过顶部盖板传递到外界),因此电缆最高导体温度变化较小;而当回填细沙在潮湿状态下时,电缆最高导体温度随中间沟壁的减小升高了5.47 ℃,当回填细沙为干燥状态时温度则升高了17.24 ℃。电缆最高导体温度的变化符合前述对不同工况下电缆散热情况差异的分析。

图5 中间沟壁厚度变化对电缆最高导体温度的影响
2.3 双沟四回路电缆的优化敷设方案
由前述分析可知,采用双沟四回路敷设方案时,靠近电缆沟中间沟壁的两回路电缆(回路2和回路3)发热较为严重,限制了双沟敷设电缆的载流量。针对这个问题,本文提出将靠近中间沟壁的两回路电缆放置在电缆沟底部的优化敷设方案,并在前述建立的仿真模型基础上,分析优化方案的改善效果。
采用优化敷设方案后,回路2和回路3放置在电缆沟底部的中间位置,回路内电缆间距不变,此时双沟四回路电缆的几何模型如图6所示。
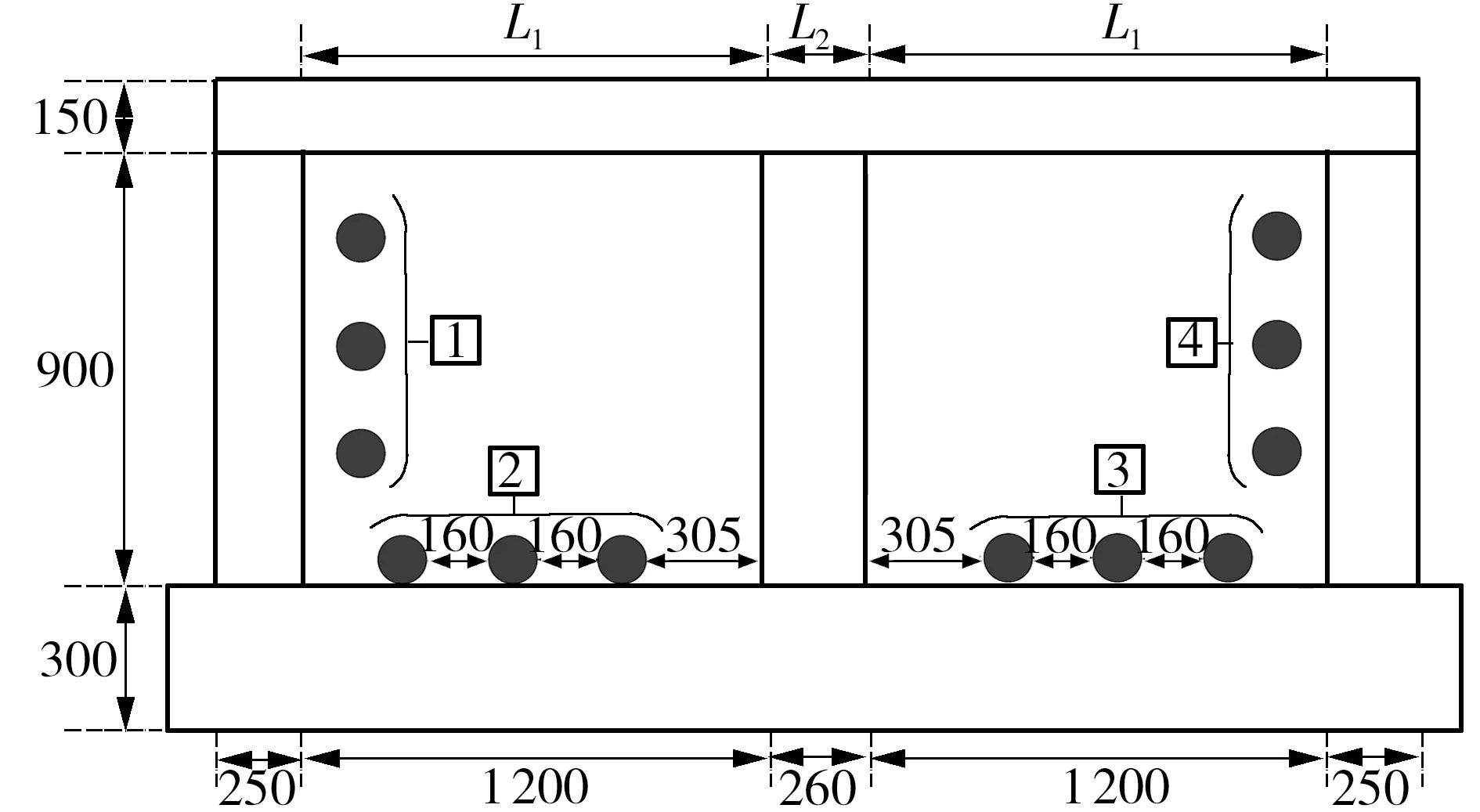
图6 优化敷设方案的几何示意图(单位:mm)
电缆沟内未回填沙土时,在负荷保持不变的情况下,对比之前的敷设方案,采用优化敷设方案后的双沟敷设电缆最高导体温度下降了1.70 ℃,载流量提升了13 A。
电缆沟内回填细沙时,采用优化敷设方案后,不同沙土热阻系数下双沟敷设电缆载流量提升情况如图7所示。
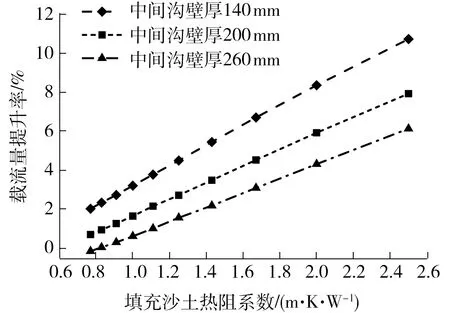
图7 不同工况下改进敷设方案的载流量提升情况Fig.7 Improvement of the ampacity under various conditions

中间沟壁厚度的减小有利于降低电缆沟建设成本。实际运行情况下,受电缆散热的影响,回填沙土会因为发生水分迁移而变干燥[34],本文提出的优化敷设方案对中间沟壁厚度较小、回填沙土热阻系数较大的情况具有明显的改善作用,对于回填沙土的双沟敷设多回路电缆的设计有着重要的参考意义。
3 结论
(1)对于双沟敷设多回路电缆,受相互间电磁影响和散热影响,位于不同位置的电缆发热情况存在差异,靠近中间沟壁的两回路电缆发热较为严重,且位于中间相的电缆导体稳态温度最高,该位置是限制双沟敷设电缆载流量的瓶颈位置。
(2)双沟敷设多回路电缆导体温升随电缆沟宽度的减小而呈线性升高趋势,且靠近中间沟壁的电缆回路温升幅度更大。


