基于SN补偿的无线输电系统的分析及原边控制

2020-02-05杨金明邓梓颖刘润鹏孙杰杉

华南理工大学学报（自然科学版） 2020年12期

杨金明邓梓颖刘润鹏孙杰杉

(华南理工大学电力学院,广东广州 510640)

随着用电场合越来越多样化,输电的方式也不断发展,已不再仅限于传统的有线输电。近年来,无线输电技术成为研究热点,磁耦合谐振式无线输电(MCR-WPT)因其适用于中距离传输,且受空间限制的影响较小[1]而受到关注,目前已在一些领域投入使用[2- 4]。

常用的无线输电系统的结构有两线圈、三线圈[5]和四线圈[6]结构,两线圈结构简单,其效率在近距离传输时高于三线圈结构[7],因此一般对近距离输电的研究多采用两线圈结构。无线输电线圈的基本补偿拓扑有SS(串联-串联)、SP(串联-并联)、PS(并联-串联)和PP(并联-并联) 4种;另外还有改进的T型拓扑，如LCL(电感-电容-电感)、LCC(电感-电容-电容)[8]以及基本拓扑和改进拓扑的组合。文献[9]提出的二次侧补偿拓扑是在LC(电感-电容)并联谐振的基础上增加一个T型阻抗变换网络,以达到提高远距离传输功率和效率的目的。文献[10]提出了一种SN拓扑,在线圈品质因数和耦合系数都较大的情况下,将SS拓扑的副边补偿电容省去,输电线圈的效率和SS拓扑的相差不大,因此,这种拓扑可用于品质因数较大且紧耦合的发射线圈和接收线圈中,以提高接收端的集成度,减小接收端的损耗。

负载一般需要恒压供电,而不加控制时无线输电系统的接收端输出电压会随着两线圈之间的互感和负载的变化而变化,因此,为了保证输出电压恒定,需要加入恒电压控制。常见的控制方法有原边控制、副边控制以及原、副边双边控制。文献[11]提出了一种通过改变原、副边开关管导通占空比来提高输电系统在较宽工作范围内的效率的双边控制方法,但是原副边之间需要通信。文献[12]提出了一种在原、副边都引入可控开关电容(SCC)补偿结构的多接收线圈MCR-WPT系统的双边控制方法,使用该方法时原、副边无需进行通信,但是原、副边都引入SCC补偿电容,接收端结构较复杂。文献[13]提出了一种只检测原边的电压量和电流量,以计算发射线圈和接收线圈之间的互感和输出端电压的原边控制方法,简化了副边的结构,达到了输出电压或电流恒定的效果。文献[14]提出了一种在无线励磁同步电动机原边检测电流,从而计算副边电流的方法,因而无需在旋转的副边安装检测器件,降低了旋转部分的设计难度。

本文提出一种基于SN补偿拓扑的原边检测控制方法,通过检测原边线圈的输入电压和电流以及两者之间的相角差,计算出实际互感值和接收线圈的实际输出电压,从而得出发射端逆变器移相控制的延迟角,达到控制输出电压的目的,以期为近距离的静态无线输电系统设计提供参考。

1 理论分析

1.1 基于SN补偿的拓扑分析

基于SN补偿的两线圈拓扑如图1所示。主要包括直流电压源Udc、全桥逆变电路(由开关管S1-S4组成)、发射端补偿电容C1、发射线圈自感L1、发射线圈和接收线圈之间的互感M12、发射线圈电阻R1、接收线圈自感L2以及接收线圈电阻R2。实际的无线输电电路中,在接收侧的整流电路之前一般连接功率因数校正电路,令整流电路及其后的负载呈现纯阻性,因此只用纯电阻RL来等效负载,RL满足[15]:

(1)

式中，RD为整流桥后级直流负载的等效电阻。

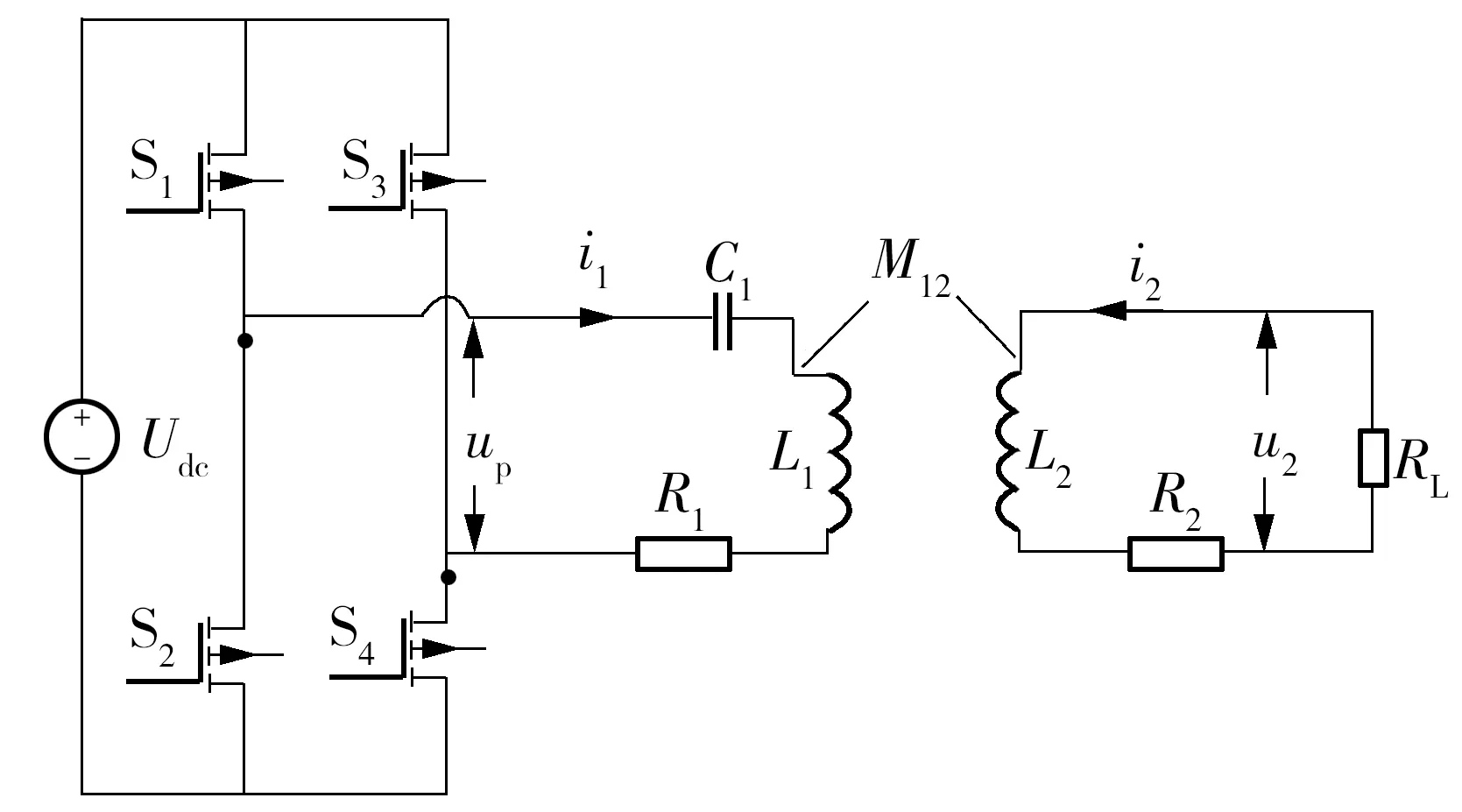
图1 基于SN补偿的两线圈拓扑Fig.1 Two coil topology based on SN compensation

图1中,up为发射线圈侧输入电压,u2为负载两端的电压,i1为发射线圈的电流,i2为接收线圈的电流。Up表示发射线圈侧输入电压的基波分量有效值,由傅里叶级数分解可知Up满足:

(2)

式中,θ为逆变器的延迟角,其具体定义在1.3节说明。

由于谐振电路的选频特性,且经过理论计算分析,发射线圈和接收线圈侧的电流总谐波含有率均小于5%,因此即使不计谐波电流的影响，其对后面的计算分析影响也不大,可以用基波近似法(FHA)对电路进行分析[16]。假设电路谐振的角频率为ωr,C1按照文献[10]的方法取值时,由于其未能完全补偿L1,因此系统的效率低于C1按照完全补偿L1的要求取值时,在本文的分析中,C1按照完全补偿取值:

(3)

I1、I2分别表示发射线圈和接收线圈的电流的基波分量有效值,电路工作在谐振状态时,发射线圈侧和接收线圈侧的回路方程可表示为

(4)

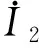
(5)

因此,接收线圈侧回路反映到发射线圈侧的反映阻抗Zre为

(6)

发射线圈侧回路的输入阻抗Zin可以由Up和I1计算得到:

(7)

U2表示负载两端的电压的基波分量有效值,负载两端的电压为

(8)

1.2 互感检测和输出电压计算

对于静态无线输电系统,其发射线圈和接收线圈之间的互感值虽然不会时常变化,但是两线圈的位置偏移会造成互感偏移设计时设定的值,且实际负载也有可能与设计的负载有差异,由式(8)可知,互感和负载电阻的变化都会影响到输出的电压。如果能通过检测发射线圈回路的电压量和电流量来确定实际的互感值以及实际的输出电压,就有可能实现对输出电压的控制。

由式(7)可知Zin和Zre的关系可以表示为

(9)

由式(6)可分别计算Zre的实部和虚部:

(10)

将Zre的虚部与实部相除,可得:

(11)

式中,Q2为接收线圈的品质因数。

由式(11)可得:

(12)

将式(12)代入式(10)可得:

(13)

由式(5)可知:

(14)

因此,可以计算负载两端电压为

(15)

由式(9)-(15)可知,对于参数确定的两线圈SN无线输电系统,只需知道发射线圈侧的Up、发射线圈的I1及两者之间的相角差φ1,即可计算出M12和U2。

1.3 移相控制延迟角的计算

本文采用移相控制的方法,通过控制全桥逆变电路开关管的导通角来控制交流电压的有效值,进而控制负载两端的电压。移相控制的原理如图2所示。

uG1-uG4分别是给开关管S1-S4的触发信号,其中，给开关管S1和S2的触发信号是相反的,给S3和S4的触发信号也是相反的,但是给S4和S3

图2 移相控制原理Fig.2 Principle of phase shift control

的触发信号不是分别与给S1和S2的相同,另外,给S3的触发信号比给S1的延迟了θ的电角度,输出的交流电压不是正负各为180°的脉冲,而是正负各为θ的脉冲,因而输出电压的有效值减小。如果能够计算出延迟角θ,就能够控制Up,从而达到控制U2的目的。

假设输出电压的参考值为U2ref,则要令输出电压达到U2ref,由式(15)可知发射线圈侧回路的电流参考值应为

(16)

发射线圈侧输入电压的基波分量有效值的参考值为

(17)

由傅里叶级数分解得移相控制的输出电压为

(18)

式中，θref为令发射线圈侧输入电压的基波分量有效值为参考值时的延迟角,由(18)可得:

(19)

计算出延迟角后,将延迟角转化为S3比S1延迟导通的时间反馈到开关管的触发信号,就可以使接收线圈侧的输出电压达到参考值,从而实现恒压控制。延迟时间的计算为

(20)

1.4 基于SN补偿的效率分析

无线输电系统的效率是衡量系统的传输能力的指标,也是限制输电距离增加的重要因素。基于SN补偿的无线输电系统的效率可表示为

(21)

由式(5)可得:

(22)

将式(22)代入式(21)得:

(23)

由式(23)可知,当电路的参数确定时,无线输电系统的效率与RL和M12有关,从式(23)中可以直接看出,M12越大,效率越高。对η关于RL求偏导,令偏导数为0,求得负载电阻RL为

(24)

由式(24)可知,当RL达到某一值时,系统能够获得最佳效率,令系统获得最佳效率的RL和M12有关,M12越大,则获得最佳效率时的RL越大。图3是基于SN补偿的两线圈无线输电系统的效率η与M12和RL的关系。

图3 效率η与M12和RL的关系Fig.3 Relationship between η,M12 and RL

由图3可知,η与M12和RL的关系与理论分析一致,η随着M12的增大而增大,当M12增大到一定程度时,η的增加速度变得缓慢;当M12一定时,η在某一RL下取得最大值,令系统获得最大效率的RL值随着M12的增大而增大。

综上所述，系统的效率随互感值的增大而增大,当负载电阻值增大时,效率先增大后减小。

2 仿真与实验

由前文的理论分析可以确定系统的控制策略,图4是移相控制结构图,控制环节的输入量只有发射线圈侧的交流输入电压up、电流i1以及负载两端的参考电压有效值U2ref,输出的延迟角转化为延时输入到矩形波发生器,给全桥逆变器的4个开关管提供正确的触发信号,从而达到控制交流输入电压基波分量有效值的目的。

图4 移相控制结构图Fig.4 Phase-shifting control structure chart

2.1 开环和闭环仿真

应用Simulink仿真平台进行仿真验证,各元件的参数如表1所示。

1)fr为电路的开关频率。

2.1.1 开环仿真

为了验证系统开环时,在负载动态变化的过程中计算的互感和计算的输出电压符合实际值,令M12不变,而令RL先从38.6 Ω减小为20.7 Ω,再增大为50.7 Ω,计算的电感值M12cal、实际输出电压值U2和计算的输出电压值U2cal如图5所示。

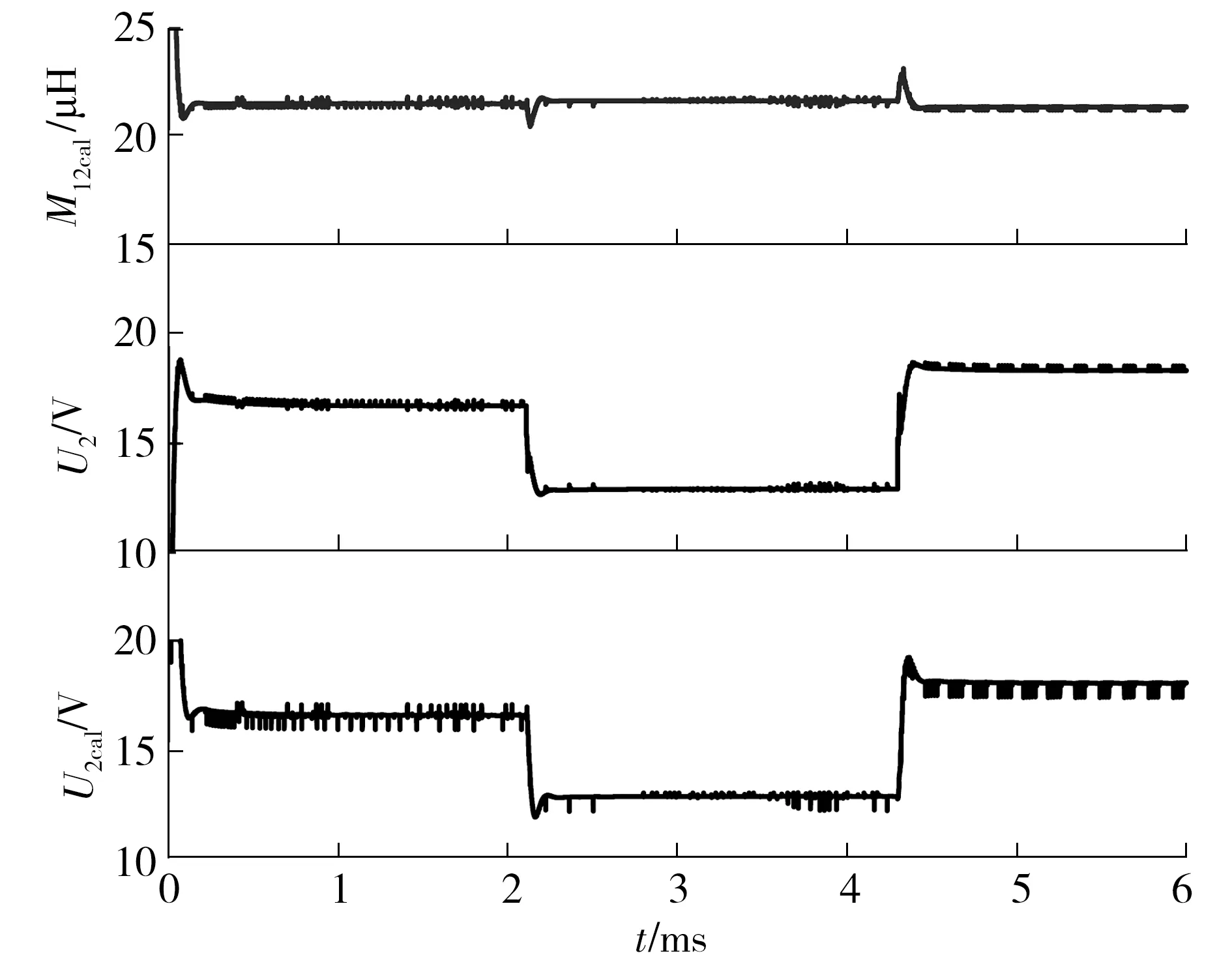
图5 RL变化时M12cal、U2和U2cal的动态变化Fig.5 Dynamics of M12cal、U2 and U2cal when RL changes

从0 ms到2 ms的过程中,RL为38.6 Ω,在2 ms时RL减小为20.7 Ω,在4 ms时RL为50.7 Ω。电阻变化前后计算出来的M12cal分别为21.542、21.669和21.389 μH,相对于实际M12的误差分别为0.623%、0.037%和1.329%,都在2%以内。

U2是在负载两端实际测得的电压基波有效值,而U2cal是通过Up、I1和φ1计算得到的负载电压基波有效值。RL变化的过程中,实际测得的U2分别为16.735、12.914和18.348 V,计算得到的U2cal分别为16.580、12.862和18.055 V,前后3次计算得到的U2cal相对于实际测得的U2的误差分别为0.926%、0.403%和1.597%,3次误差均不超过2%。

在RL变化的动态过程中,计算的M12cal和U2cal均能在变化后的0.5 ms内达到较准确的值且趋于稳定,因此在RL变化时,系统能够较准确地计算出互感值和输出电压值。

为了验证当互感发生变化时系统仍能准确计算互感和输出电压,令RL保持为38.6 Ω,M12从5 μH到50 μH改变10次。计算得到的互感值M12cal以及计算的相对误差eM如图6所示。由图6可知,当M12较小即耦合系数较小时,计算的相对误差较大,但不超过5%;M12增大时,计算的相对误差逐渐减小,当M12在10 μH以上时,误差不超过1%。

图6 M12变化时的M12cal和eMFig.6 Curves of M12cal and eM varying with M12

M12变化时，实际测得的U2、计算得到的U2cal以及计算的相对误差eU如图7所示。由图可以知道,当M12在10 μH以上时,计算的相对误差在5%以内,且随着M12增大,相对误差逐渐减小。因此,M12在一定的范围内时,可以获得比较准确的计算结果,且M12越大,计算结果越准确。

图7 M12变化时的U2、U2cal和eUFig.7 Curves of U2、U2cal and eU varying with M12

为了验证当RL发生变化时系统仍能准确计算M12和U2,令M12保持为21.677 μH,RL从5 Ω到50 Ω改变10次。实际的M12、计算得到的M12cal以及计算的相对误差eM如图8所示。由图8可知,在RL变化的过程中,计算的M12cal总是与实际的M12很接近,最大相对误差不超过0.2%。

图8 RL变化时的M12、M12cal和eMFig.8 Curves of M12、M12cal and eM varying with RL

RL变化时，实际测得的U2、计算得到的U2cal以及计算的相对误差eU如图9所示。由图可以知道,当RL大于10 Ω时,计算得到的U2cal的相对误差小于0.5%,RL较小时计算的相对误差稍大,但不超过2%。以上的分析说明了当RL在一定的范围内变化时,系统能够较准确地计算互感值和输出电压值。

图9 RL变化时的U2、U2cal和eUFig.9 Curves of U2、U2cal and eU varying with RL

开环仿真的结果表明,系统在两线圈之间的互感和负载变化时,能够通过检测发射线圈侧电压、电流计算出实际互感及接收线圈侧的输出电压。

2.1.2 闭环仿真

系统闭环时,由图4可知,要将计算得到的延时输入到信号发生器,从而使其产生所需的触发信号,改变每对开关管同时导通的时间。当系统的各元件参数与开环仿真情况相同时,由式(19)可知,arcsin符号内部分的取值范围应该为0～1,因此Upref的取值范围为0～9.003 V,这说明了移相调压的范围是有限的,由式(16)-(17)可得U2ref的范围是0～25.164 V。

为了验证移相控制调压的原理,令U2ref分别为10和20 V,两次仿真得到的θref、up和U2波形分别如图10和11所示。由图10和图11可知,当U2ref改变时,计算得到的θref发生变化,从而使输入的交流电压up波形中不为0的部分宽度改变、up的基波有效值U2改变。输出的U2比较接近设定的U2ref。

图10 U2ref为10 V时的θref、up和U2Fig.10 θref、up and U2 when U2ref=10 V

图11 U2ref为20 V时的θref、up和U2Fig.11 θref、up and U2 when U2ref=20 V

为了测试系统的调压能力,令系统的其他参数保持不变,多次改变U2ref,得到的U2和U2相对于U2ref的误差eU如图12所示。在理论的调压范围内,U2和U2ref相差较小,相对误差在5%以内。

图12 U2ref变化时的U2和eUFig.12 Curves of U2 and eU varying with U2ref

为了测试系统在M12改变的情况下能否保持恒压输出,令Udc保持为10 V,U2ref保持为15 V,RL保持为38.6 Ω不变,M12从5 μH到38 μH改变10次。仿真得到的U2ref、U2和U2相对于U2ref的误差eU如图13所示,在一定的变化范围内,U2相对于U2ref的误差较小,在5%以内,M12超出一定值后,误差急剧增大,这是因为M12的改变使调压范围改变了,U2ref已超出此时的实际调压范围。

图13 M12变化时的U2ref、U2和eUFig.13 Curves of U2、U2ref and eU varying with M12

为了测试系统在RL改变的情况下能否保持恒压输出,令Udc保持为10 V,U2ref保持为15 V,M12保持为21.677 μH不变,RL从23 Ω到65 Ω改变10次。仿真得到的U2ref、U2和U2相对于U2ref的误差eU如图14所示,在一定的变化范围内,U2相对于U2ref的误差较小,在5%以内,RL小于一定值时,误差急剧增大,这也是因为RL的改变使调压范围发生了变化。

图14 RL变化时的U2ref、U2和eUFig.14 Curves of U2、U2ref and eU varying with RL

结合图13和14可知,当M12或RL稍微偏离设定值时,系统仍然能够保持输出电压恒定。

闭环仿真的结果表明,系统可以通过移相控制来调节输出电压,但调压范围有限,在系统参数确定且输入直流电压一定时,调压范围由互感和负载决定,因此,只能在互感和负载在一定的范围内变化时保持输出电压恒定。

2.2 开环和闭环实验

基于SN补偿的两线圈无线输电系统的实验装置如图15所示,直流输入电压Udc=10 V,全桥逆变器由4个MOSFET管IRFP260N组成,由数字信号处理器(DSP) TMS320F28335PGFA提供100 kHz占空比为50%的PWM信号,经过悬浮驱动器IR2110驱动。发射线圈和接收线圈均由规格为0.1 mm×450股、线径为3 mm的高频利兹线绕制10匝而成,线圈形状为圆角矩形,外边长为30 cm,内边长为24 cm,外圆角半径为8 cm,内圆角半径为5 cm,发射线圈和接收线圈之间的距离为4.5 cm,补偿电容采用高频低损耗的薄膜电容并联而成,负载为21.3 Ω的直流电阻。系统的各参数如表2所示。

图15 实验装置Fig.15 Experimental device

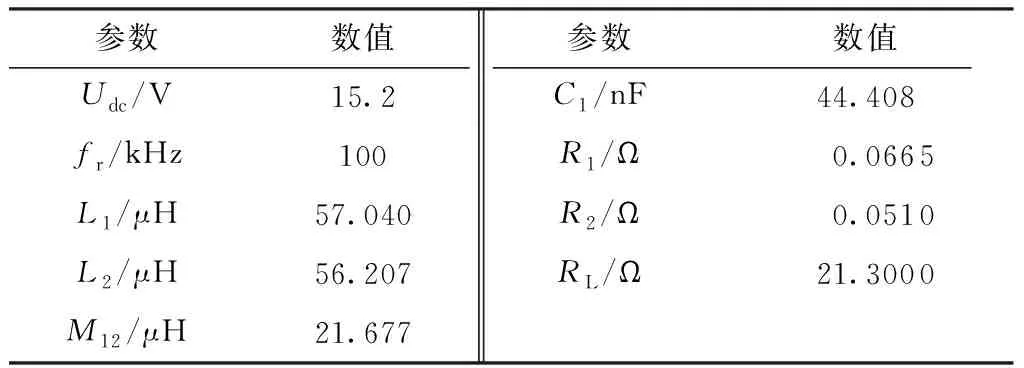
表2 实验系统各参数Table 2 Parameters of experimental system

2.2.1 开环实验

开环实验时,图16(a)为测得的发射线圈侧输入交流电压up和电流i1的波形,图16(b)为up和i1的局部放大图,显示了up和i1的基波相位差φ1,图16(c)为负载电阻两端的电压u2的波形。由图16(a)可知,up的峰值为15.2 V,i1的峰值为3.8 A;由图16(b)可知，φ1为-1.036 7 rad;由图16(c)可知，u2的峰值为25 V。将以上数据代入式(2)-(15)中计算,得到M12cal=22.855 μH,U2cal=19.216 8 V,U2=17.677 7 V,M12cal相对于M12的误差为5.435 3%,U2cal相对于U2的误差为8.706 5%。

实验证明,系统在开环运行时可以比较准确地估计发射线圈和接收线圈之间的互感值以及负载两端的电压值。实验计算得到系统的效率为78.38%,说明系统在实际中可以达到较高的效率。

2.2.2 闭环试验

系统闭环时,令U2ref= 18.5 V,得到的全桥逆变器的S1和S3的触发信号如图17所示,发射线圈侧输入交流电压up的波形如图18(a)所示,负载电阻两端的电压u2的波形如图18(b)所示。