基于自适应遗传算法的模拟集成电路设计

杨青

（兰州空间技术物理研究所 甘肃省兰州市 730030）

电子产品已经充分融入到了社会中的各个领域，影响着人们的日常生活以及工作。当前集成电路的工艺技术发展十分迅速，并且人们对于数字模拟混合的电路以及相关的系统需求逐渐增加，数字集成电路与模拟集成电路由简短的电路结构、小规模逐渐向着高密度、大规模的集成电路方向发展[1]。传统的数字、模拟集成电路设计要求研究人员具备更丰富的设计经验以及背景知识，设计周期较长，并且人工干预较多，导致数字、模拟集成电路的优化设计逐渐具有更高的挑战性。对于当前的数字集成电路而言，经过研究人员和技术人员长时间的研究，已经存在许多较为成熟的自动化设计工艺以及工具，能够在更短的时间内将电路设计者的思想转换为实际的电路拓扑或物理版图，通过相应的先进工艺手段完成对数字集成电路的设计[2]。但目前模拟集成电路的自动化设计水平以及工具等方面与数字集成电路相比较为匮乏。传统模拟集成电路采用的是将电路性能评估器与数字优化机相结合的设计方法，在对模拟集成电路参数的优化过程中通常采用下降单纯形法以及模拟退火法等优化算法。但上述方法在实际应用中存在较多问题，主要包括：需要尽可能提供更好的起始迭代点，否则迭代次数增加；由统计优化算法向确定性优化算法进行过渡的过程中退火温度无法确定，容易存在不收敛等问题。因此，本文针对上述模拟集成电路存在的问题，开展基于自适应遗传算法的模拟集成电路设计研究。

1 模拟集成电路设计

电路阻容滤波器是模拟集成电路中的核心部分，因此在对模拟集成电路设计时，第一步是对其阻容滤波器进行设计。对于任何复杂滤波网格结构而言，都需要若干个结构简单的一阶和二阶滤波电路的共同组成[3]。针对当前模拟集成电路运行特点，本文选用一阶无源低通滤波器，该滤波器的具体结构示意图如图1 所示。

根据图1 一阶无源低通滤波器结构示意图可以看出，可进行调节的参数元件数为3 个，而在滤波器的设计过程中通常选用温度系数较小，并且精度较高的电阻[4]。因此在对模拟集成电路阻容滤波器设计过程中，本文将其电阻的取值设定为2K～150K 范围之间。将电阻的搜索空间定义为在2K～124.6K范围之间，步长设置为0.2K。电容选择损耗较小的优质电容，将电容的取值设定在大于15pf，根据模拟集成电路滤波器的截止频率公式计算对截止频率进行计算，公式为：

公式（1）中，k 表示为滤波器截止频率；R 和R'表示为滤波器中的两个阻值；C 表示为滤波器电容。根据公式（1）得出，本文选用的一阶无源低通滤波器的截止频率为150K 左右[5]。因此，能够估算得出电容的取值范围应在15pf～1024pf 范围之间，其步长为15pf。因此，根据上述论述结合自适应遗传算法得出染色体长度为60 位二进制固定代码，其染色体如图2 所示。

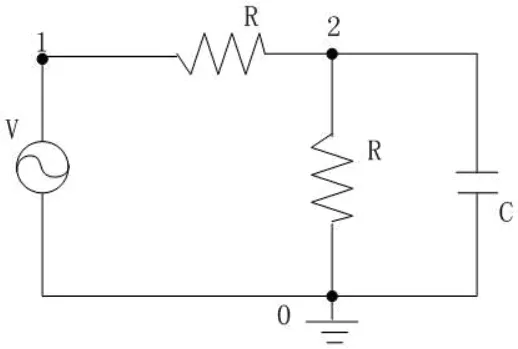
图1：一阶无源低通滤波器结构示意图

图2：基于自适应遗传算法的滤波器染色体

在模拟集成电路中通常包括多项性能兼容指标，即多目标，因此本文采用将多个子目标以加权和的形式展现，从而将多目标问题转换为单目标问题[6]。在对单目标问题分析过程中，利用滤波器的频率响应曲线与理论滤波器响应曲线拟合，从而得出针对单目标优化的可靠性，并得出滤波器的自适应函数，如公式（2）所示：

公式（2）中，fit(s)表示为滤波器的自适应函数；s 表示为自变量；s 表示为采样频率；c 表示为常数，通常情况下为1，主要目的是为防止自适应函数的分母为0。公式（2）在理想滤波器的条件下，其最大数值为30000。

1.2 基于自适应遗传算法的电路运算放大器参数选择

在完成上述模拟集成电路阻容滤波器设计的基础上，根据该类型滤波器的性能要求，对电路运算放大器参数进行选择。在相同结点数以及相同元器件数目的条件下，根据不同运行指标的变换，对模拟集成电路低通、高通以及带通三组形式的放大器参数进行选择。为了满足模拟集成电路的自动化程度，本文对电路中的节点数量、元器件的种类以及组容器件数目进行明确的规定和限制[7]。根据自适应遗传算法对电路运算放大器参数进行二进制编码，根据模拟集成电路中的电容、电阻均为双端口元件的特点得出电路运算放大器的染色体编码为：Cj=[typej,nodej+,nodej-,valuej]，其中typej为1 位；nodej+为3 位；nodej-为3 位；valuej为9 位。并且，其中type 为模拟集成电路中用到的所有器件类型，由于本文设计的模拟集成电路只用到了电阻、电容两种器件，因此type 需要占用一个二进制代码。node+和node-分别表示为双端元件的两个固定节点[8]。由于本文采用的一阶无源低通滤波器其结构相对简单，以此可进行简化。由上述得出，本文设计的模拟集成电路固定节点共有8 个，node+和node-分别占用两个三位二进制代码。value 表示为对应器件的数值，占用一个九位二进制代码。每个元件占用32 位二进制染色体，则整个电路需要的染色体总长度为256 位。根据自适应遗传算法得出电路运算放大器高通、低通的适应度函数为：

表1：实验结果对比表

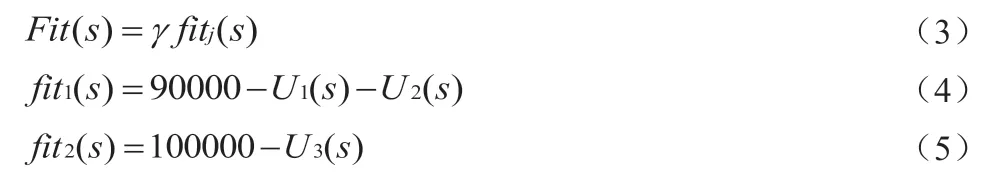
公式（3）中，Fit(s)表示为电路运算放大器总适应度函数；γ表示为常数1；j 表示为模拟集成电路中的所需的元器件个数。公式（4）中，fit1(s)表示为电路运算放大器高通适应度函数；U1和U2表示为高通电路中的两个不同电压。公式（5）中，fit2(s)表示为电路运算放大器低通适应度函数；U3表示为低通电路中的电压。根据自适应遗传算法中的先定结构，后定参数的思想，染色体当中的各个基因位对于整体的适应度函数影响并不一定相同，甚至差别较大，因此本文设置type 与node+、node-的基因位对模拟集成电路的电路性能影响大，value 基因位对电路的性能影响小。

2 实验论证分析

2.1 实验准备

本文选用ongoingTKSC0.10 微米工艺库，其工作电压为4.5V，计算机选用Uicrv-18 工作站，其CPU 大小为500，内存为512M，为本文实验提供实验环境。选取的种群样本大小为100，进行代数为200 代，设置初始交叉概率为0.98，初始变异概率为0.25。分别利用本文提出的基于自适应遗传算法的模拟集成电路设计方法与传统模拟集成电路设计方法对该电路进行设计。在实验过程中，考虑到直流增益的问题，将电路的转换速率设置为本文对比实验的验证指标。

2.2 实验结果与分析

根据上述实验准备，将两种设计方法设计的模拟集成电路进行应用，并将其应用效果中的转换速率指标进行记录，绘制成如表1所示的实验结果对比表。

根据表1 中5 次对比实验的实验结果可以看出，利用本文设计方法设计出的模拟集成电路与传统设计方法设计出的模拟集成电路相比，转换速率更高，充分达到预期要求效果。因此，通过对比实验证明，利用本文方法设计出的模拟集成电路与传统模拟集成电路相比实现了优化，并结合自适应遗传算法解决了多目标优化的方向性问题，进一步提高了设计精度。由于该设计思路更贴近于模拟集成电路工艺的设计思想，因此具有更高的应用价值。

3 结束语

本文针对模拟集成电路工艺设计存在问题，提出一种全新的设计方法，但当前大多数电路的结构始终保持不变，因此需要从一个工艺转变为另一个工艺。对于模拟集成电路而言，工艺上的改变往往会造成电路各项性能上的变化，因此需要经验丰富的电路设计人员对其参数进行不断地调整，从而使模拟集成电路的设计更满足企业需要。