双干扰项下参数对线性增额寿险模型的影响

沈 丹，介龙梅，庄 严

（营口理工学院 电气工程学院，辽宁 营口 115014）

0 引言

从投保人投保到保险公司理赔这一个周期中，寿险赔付的利率一般以银行利率为基本利率.我们都知道，如果保险公司推出的产品定价的利率低，那么保费的收益就会很高，人们的购买能力也会相继提升；如果产品定价的利率高，那么保费的收益就会降低，购买能力也会下降.可见对于的产品的定价与利润都与利率息息相关.所以对于保险公司如果想获得丰厚的利润，就要先做一个合理的预测，建立可行性的寿险模型，通过对数据的分析准确的去调配资金，最终不但使投保人获利也使保险公司也能盈利.

1 双干扰项下增额寿险模型

1.1 利息累计函数

息力累计函数R(t)［1］，其中B(t)为Brownian运动，| B(t )|是标准反射Brownian［2］运动(σ2=1 )，N(t)是关于参数λ的Poisson运动过程，且β、γ是与t无关的随机变量或常数.

1.2 随机利率下n年定期即时给付增额寿险模型

上式为定期即时给付增额寿险模型［3］，其中R()t为利息累计函数；α＞0称为增长系数，特别的当α=1，称为n年标准定期增额寿险［4］模型.

2 随机利率下给付现值一阶矩

在DeMoivre死亡力下，0 ≤ t＜ n时，将式（3）代入式（4）

即：E(ZT)=EδEγEBET(ZT)

3 双干扰项下参数变化对线性增额寿险的影响

考虑5，10，15，20年定期连续型线性增额寿险，假设保费以每年10%递增( )α=0.1 ，令b=1，取银行常见利率δ=0.025代入式（4）中，令目标函数

现取六组不同参数数值，经过MATLAB模拟运算，得到M的不同数值，

根据上面算例所得数值，得到如下表格（表1～5）.

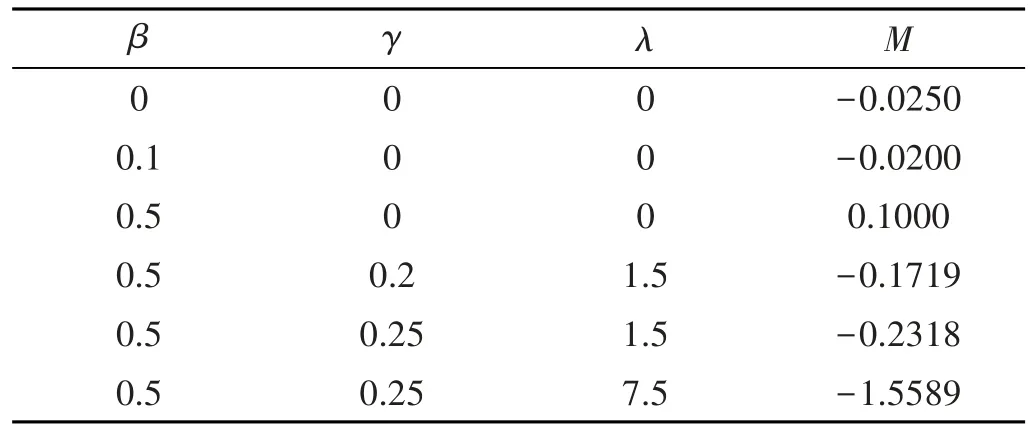
表1 不同参数下的M数值表

表2 投保人x=20不同参数M下给付现值变化表

表3 投保人x=30不同参数M下给付现值变化表

表4 投保人x=40不同参数M下给付现值变化表

表5 参数M=-0.1719不同年龄、不同定期下给付现值变化表

为了能够更加清晰直观的观察随着投保期越长、投保年龄越大给付现值的数值变化规律，现将以上数值表对应生成曲线图：

根据《中国人寿保险业经验生命表2000-2003》（非养老业务）中的死亡率数据当息力累计函数含有类似Brownian及修正后的类似Poisson双干扰项时，分析上述表格和图形有如下结论：

（1）此增额寿险给付现值模型显然为关于增长系数α＞0的单调增函数.

（2）由上述数值表与曲线图可观察出当多个参数对给付现值寿险模型进行扰动时比单参数更加剧烈.

（3）由图1，图2，图3可观察出对于参数的变化出现了一个失控点β=0.1000，其他参数点处表现正常，出现随着投保期的增加给付现值呈现递增趋势.在同一个投保期内，辅助参数M去除失控点后在不断变大的过程中给付现值呈现了递减的趋势.

（4）当息力累计函数只含有类似Brownian干扰项时，其贡献值随着β的增加呈现先上升再下降的趋势.

（5）根据表5在M=-0.1719处，

1）当投保人年龄为20岁时，对应n=5，10，15，20年定期增额寿险，较前一期限下增幅分别为58.82%，20.00%，9.28%；

2）当投保人年龄为30岁时，对应n=5，10，15，20年定期增额寿险，较前一期限下增幅分别为71.23%，24.80%，12.82%；

3）当投保人年龄为40岁时，对应n=5，10，15，20年定期增额寿险，较前一期限下增幅分别为73.10%，26.29%，16.45%.

可见对于同一投保人，随着时间的增加，给付现值的增幅出现下降趋势.

（6）息力累计函数含有类似Brownian及修正后的类似Poisson双干扰项时，其贡献值为负，对给付现值波动影响较大，随着参数γ的增加整体呈现先上升再缓慢下降的趋势.

（7）其他参数不变的条件下，随着扰动次数越频繁（λ越大），给付现值下降越快.

综上可知，此随机利率下连续型线性增额寿险模型含有较多干扰项时，利率波动呈现缓慢下调趋势，但随着投保期越长，投保年龄越大，回报率仍然呈上升趋势，对于较长周期的增额寿险有着很强的现实意义与指导意义.

注：观察表6与表7，在同一参数M=-0.1719下，将投保人年龄为20岁与40岁、年龄为30岁与40岁的给付现值进行Chi-square假设检验，通过SPSS统计软件计算出p→1＞0.05，故无显著差异.

表6 参数M=-0.1719下投保人年龄20岁与投保人年龄40岁给付现值卡方检验

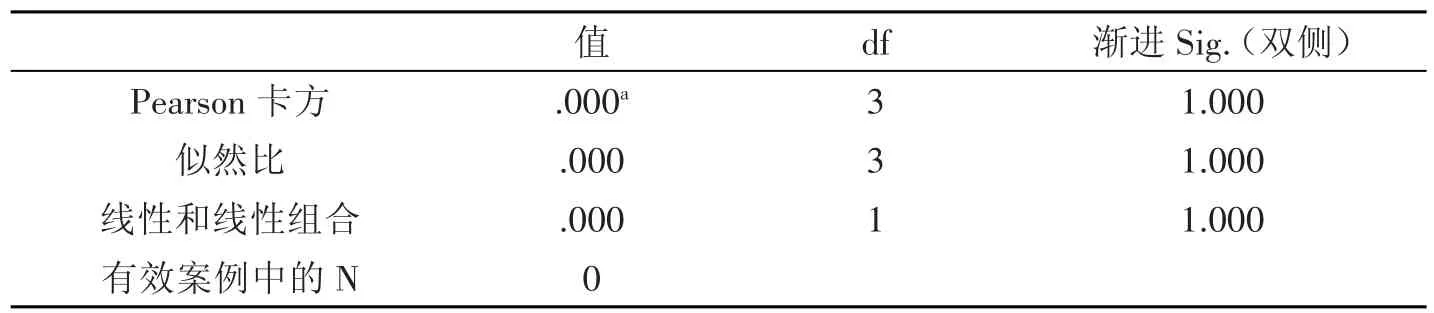
表7 参数M=-0.1719下投保人年龄30岁与投保人年龄40岁给付现值卡方检验