轨道车辆通过钢轨凹坑时的响应分析

周素霞，孙 锐，刘金朝，白小玉，刘静远

(1. 北京建筑大学 机电与车辆工程学院， 北京 100044；2. 城市轨道交通车辆服役性能保障北京重点实验室， 北京 100044；3. 中国铁道科学研究院 基础设施检测研究所， 北京 100081)

世界各国轨道交通系统钢轨都存在凹坑、波磨等各种病害。钢轨凹坑是滚动接触疲劳的主要伤损形式之一，通常被认为是表面源钢轨短波病害，最初是由钢轨表面微小压痕演变而来[1]，如不及时处理，易导致钢轨断裂。因为列车经过带有一定不平顺的线路时，会产生不同频率的轮轨接触力,由于接触力的变化，特定钢轨病害会加剧某一波长的振动幅值。而目前我国高速铁路任务繁重，某些病害不能被及时发现及处理，从而在车轮经过数次后，病害加剧，甚至可能发展成更严重的钢轨病害形式。这不仅会降低列车乘坐舒适性，还会危害行车安全，且钢轨病害导致的接触力增加也会直接影响铁路部门的线路维护成本。荷兰是欧洲铁路路网规模较大国家之一，运营里程约6 500 km，荷兰铁路每年由钢轨凹坑产生的成本高于5 000欧元/km，由此可见，钢轨凹坑是一个亟待解决的问题。

针对此问题，文献[2]利用非线性动力有限元分析软件LS-DYNA 3D建立高速铁路凹坑车轮-轨道耦合系统有限元模型，仿真计算列车通过凹坑时的动力学响应。结果表明加速度计算值与实测值存在较好的对应关系，以此研究钢轨凹坑对列车动力学性能产生的影响。文献[3]建立了车辆/轨道横向垂向耦合动力学轮轨滚动接触力学和钢轨材料摩擦磨损模型为一体的钢轨波磨计算模型，利用该方法分析了曲线钢轨顶面内侧具有横向凹坑对初始波磨形成的影响。研究表明当车辆通过具有横向凹坑的曲线钢轨时，轮对和钢轨之间发生瞬态冲击振动引起钢轨接触面产生不均匀磨损而形成初始波磨。文献[4]采用显式有限元算法建立三维高速滚动瞬态接触模型，分析牵引系数使钢轨发生不均匀磨损或塑性形变的关系。

以上算法均采用单轮模型，利用对称边界条件替代整条轮对，而本文采用Abaqus有限元分析软件，建立了双车轮轮轨三维滚动接触模型，采用显式动力学算法，计算列车通过钢轨凹坑时的轮轨接触力、轴箱加速度等数据，分析凹坑对轮对造成的冲击响应。本文的双轮模型是为了考虑车轮滚动过程中横向运动造成的影响，使结果更为精确。

1 轮轨滚动接触有限元模型

1.1 模型的建立

采用Abaqus有限元分析软件建立轮轨高速滚动有限元模型，如图1所示。模型采用三维实体单元建立，车轮踏面为S1002CN，直径为920 mm，钢轨廓形为CN60，轨底坡为1∶40，轨道板为CRTS Ⅲ型轨道板。轮轨滚动摩擦系数为0.45，且轮轨接触作用采用面面接触算法。一系悬挂以上质量简化为质点，轴重12 t。整个轨道长5 m，考虑实际情况中扣件及以下轨道部分对轮轨滚动的影响，建模考虑了扣件及轨道板结构[5-6]。扣件采用弹簧-阻尼单元模拟。

图1 轮轨高速滚动有限元模型

在动力学分析模块中，采用显式计算方法，通过修改载荷幅值的方式在一个分析步中完成轴重的施加与车轮的滚动。车轮从初始位置到钢轨凹坑区之间存在一段标准廓形轨道，目的是使车轮在滚过凹坑区之前可以达到稳定接触状态[7]。Abaqus有限元分析软件中使得网格转动或平动的方式有两种，一是利用边界条件，二是添加初始速度场。初始速度场只能添加于初始分析步中，无法保证车轮在滚动至凹坑区之前就达到稳定滚动状态。故本次计算采用施加边界条件的方法使得车轮滚动。车轮滚动速度为150 km/h，与凹坑存在区段车辆运行速度保持一致，同样施加于模型的边界条件还有轨道板底部的完全约束，约束钢轨除垂向位移以外的5个自由度[8]。车轮凹坑病害几何数据采用我国某高铁线路上的实测数据，即深度为0.02 mm的椭圆形凹坑，设置于右侧钢轨表面，如图2所示。规定车轮进入凹坑处为“凹坑前”，离开凹坑处为“凹坑后”。

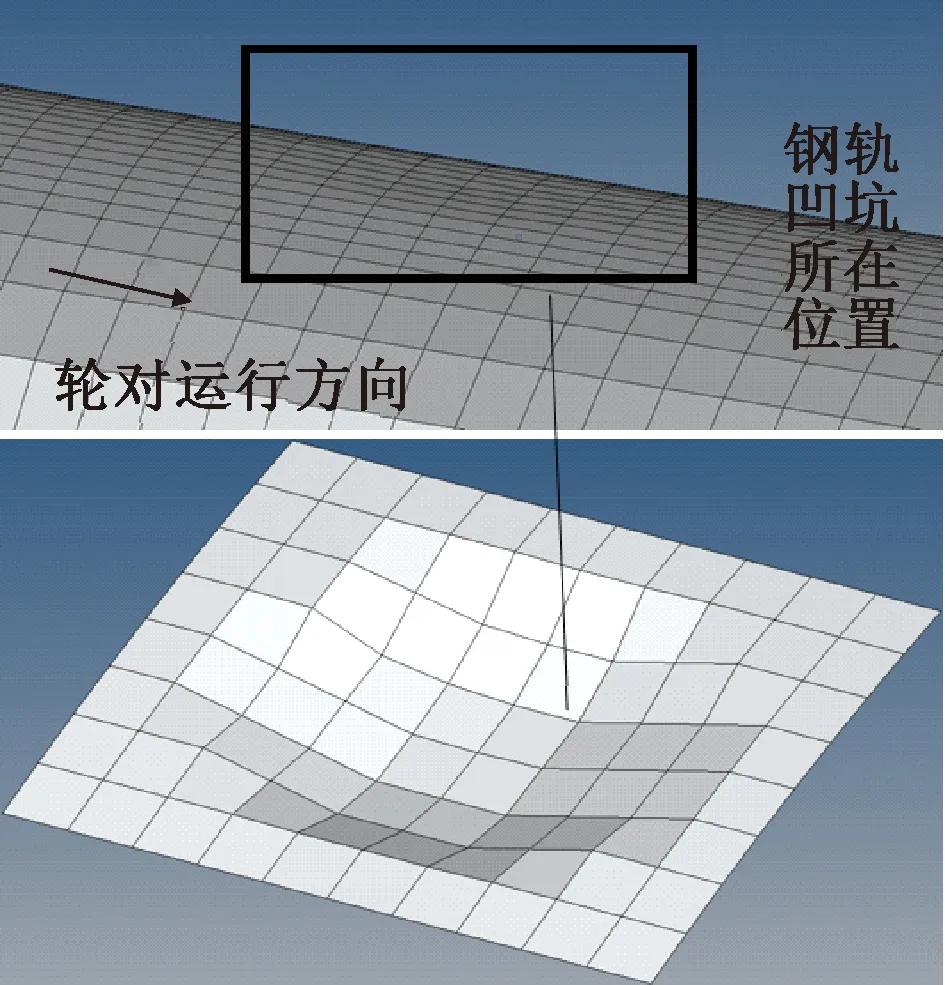
图2 凹坑位置及垂向位置扩大10倍后的型面

车辆轴箱刚度和阻尼采用Abaqus相互作用模块中自带的“弹簧/阻尼器”进行模拟，参照CRH380动车组实际一系悬挂参数，建立垂向刚度、阻尼和横向刚度。横向刚度作用即为考虑轮对运行过程中横向运动对计算结果产生的影响。

模型整体网格如图1所示，模型中最小网格尺寸为1 mm，主要位于钢轨凹坑处，轮轨接触面网格相对增大，而轨道板、车轴、车轮非踏面区域网格相对较大。此种网格划分模式可以保证良好的计算精度，同时也可以适当降低网格数量，减小计算时间，节省计算成本。本文采用的计算模型总共有636 910个单元，757 102个节点。

1.2 有限元计算格式

Abaqus软件中的显式非线性动态求解方法是应工程实际的需要而产生的，是一种真正的动态求解方法，在实际工程中，当惯性力非常大且随着时间变化较快时，就变成了动力学问题。本文建立的轮轨滚动瞬态接触模型就需要以动力学计算方法求解。

Abaqus/Explicit[9]中包含两种计算方法，即动力学显式与动力学隐式。动力学显式算法采用动力学方程的一些差分格式，如中心差分法、线性加速度法、Newmark法和Wilson法等，该算法不用直接求解切线刚度且不需要进行平衡迭代，故有计算速度快的优点。当时间步长足够小时，一般不存在收敛性问题。动态显式计算所需内存也比隐式要小，数值计算过程中也可以进行并行计算，用物理的方法降低模型的计算时间。

Abaqus/Explicit应用中心差分法对运动方程进行时间积分，应用前一个增量步的动力学条件计算下一个增量步的动力学条件。在增量步开始计算时，程序求解动力学平衡方程，表示为用节点质量M乘以节点加速度ü等于节点的合力，即所施加的外力P与单元内力I之差。运动方程为

Mü=P-I

在增量步开始的t时刻，计算加速度为

显式算法总是采用对角的或集中的质量矩阵，所以求解加速度并不复杂，不必同时求解联系方程，任何节点的加速度完全取决于节点的质量和作用于节点上的合力，使得节点的计算成本非常低。对于加速度在时间上进行中心差分法，在计算速度的变化时假定加速度为常数，应用这个速度的变化值加上前一个增量步中点的速度来确定当前增量步中点的速度，即

速度对时间的积分加上在增量步开始时的位移来确定增量不结束时的位移。

至此，在增量步的开始时提供了满足动力平衡条件的加速度。得到加速度后，在时间上“显式地”得到前推速度和位移[10]。

1.3 纯滚动状态设置

为了使车轮到达凹坑之前达到稳定的滚动状态，在起始位置与凹坑之间存在一段标准廓形钢轨，稳定滚动状态的评判依据为轮轨力是否平稳。为了缩短计算时间，需要在最短时间内完成车轮轴重与运动速度的加载过程，并且需要使得轮对经过凹坑之前与钢轨形成稳定的接触关系，即轮轨力是否稳定，图3为轮轨力的变化。从图3可以看出，初始计算阶段，轮轨力呈现大幅值振动情况，这说明计算初始阶段完成轴重的加载，并且存在垂向刚度和阻尼的情况下，轮对产生垂向振动，随着车轮前行，该振动被阻尼吸收，轮轨力逐步稳定在60 kN处，说明轮对在运行至凹坑之前即形成纯滚动状态。相关计算已由文献[11]利用Ansys针对荷兰钢轨凹坑完成，主要计算了车轮通过钢轨凹坑时高频范围内的轴箱振动加速度，计算结果已得到证实。

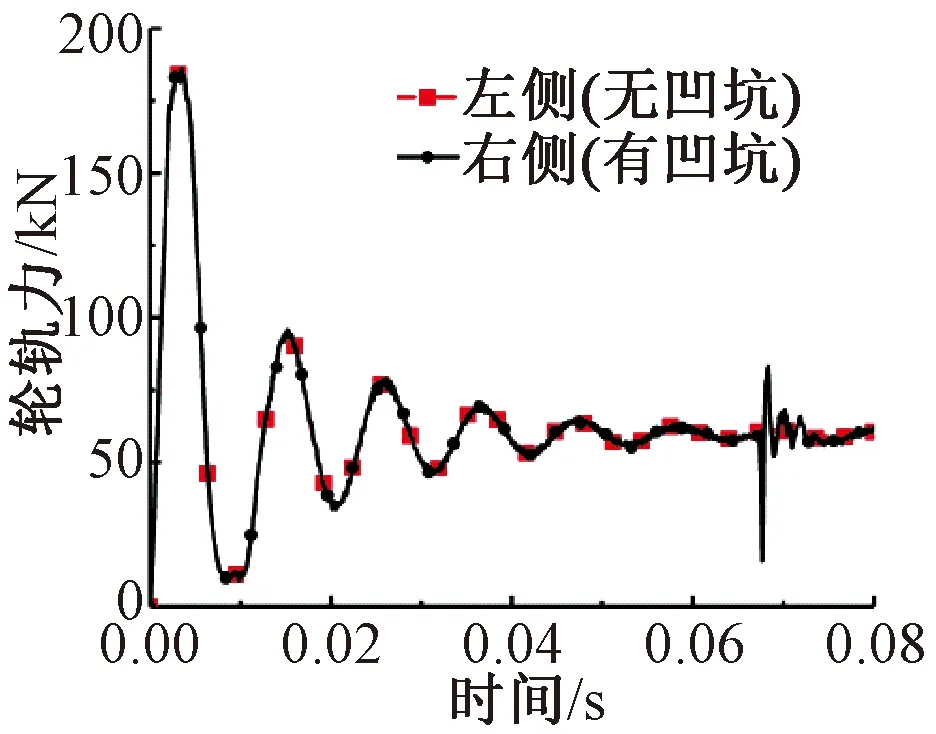
图3 车轮沿钢轨滚动时轮轨力的变化

2 计算结果分析

2.1 垂向轮轨力

根据之前的计算条件，仿真分析得到整条轮对通过钢轨凹坑时轴箱位置处的动力学响应。计算中轮轨摩擦系数为0.45，该数值为实测值，凹坑几何形状对轮轨滚动动态接触力的影响如图4所示。图中包含两条曲线，一条为存在凹坑钢轨的轮轨力，另一曲线则表示不存在凹坑一侧钢轨的轮轨力。从图4可以看出，两条曲线仅存在局部不重合情况，除此之外二者在数值和变化趋势上完全相同。车轮通过凹坑时，一侧轮轨接触面积发生变化，从而导致轮轨接触力产生激变，由于一系悬挂存在阻尼部分，故轮对会在一段时间后重回稳定状态，如图4所示。

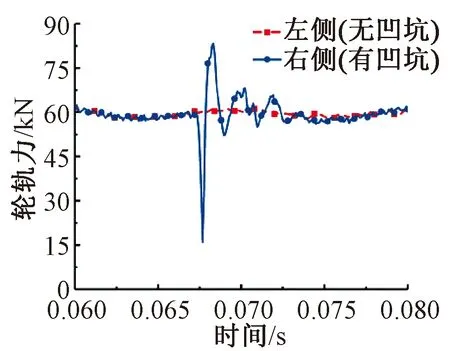
图4 车轮过凹坑时轮轨力变化

从图4可知，右侧轮轨力从稳定的60 kN突变至20 kN，随之升至80 kN，此种变化的原因是因为凹坑的存在，使得轮轨产生非紧密接触，导致轮轨力骤减。但由于一系悬挂存在阻尼作用，车轮在此发生振动，轮轨力随之产生波动，一段时间后，轮轨力又趋于平衡。另外，轮轨力没有明显变化，并且轮轨力差异会持续存在0.01 s，以车轮速度为150 km/h计算，车轮从通过凹坑后的0.42 m左右两侧轮轨力存在差异。

2.2 轴箱处垂向加速度

图5为轮对通过钢轨凹坑时垂向加速度的变化曲线。从图5可以看出，在通过凹坑后轴箱垂向加速度在车轮经过动态松弛区时峰值为±20 m/s2，而当轮对接触到凹坑的瞬间，右侧轴箱垂向加速度瞬间峰值升高至120 m/s2，最小值为80 m/s2。与轮轨力变化规律相同，在经过凹坑后的一段时间，左右两侧垂向加速度又趋于一致。

图5 轮对通过凹坑时左右两侧轴箱垂向加速度变化曲线

图6 右侧车轮轴箱处垂向加速度

图6为右侧车轮轴箱处垂向加速度的波形图，滤波范围为20～1 000 Hz[12 ]。 从图6可知，滤波后仅在0.068 s时存在波动，对其进行傅里叶变换， 976.6 Hz的主频能量最大。列车运行速度为150 km/h，故该频率会形成波长为42.67 mm的振动，在车轮通过凹坑至轮轨力重新稳定的时间内，该42.67 mm波长的振动会对钢轨造成冲击，长此以往，该区段钢轨会形成固定波长的磨耗，即波磨。时频图中能量集中位置对应车轮经过凹坑的时刻与冲击频率[13-14]。计算真实性可参考文献[15]的计算结果。

2.3 Mises应力

图7为钢轨凹坑处Mises应力云图。从图7(a)可以看出，当车轮经过凹坑时，凹坑凹陷处应力最小，为171.0 MPa，凹坑后方应力偏大，为681.7 MPa。此时应力为计算过程中最大值，轮轨稳定接触时钢轨最大应力稳定在550 MPa左右。因为凹坑为凹陷型病害，故车轮高速通过时踏面无法触及凹坑谷底，形成边缘接触，从而产生冲击振动。图7(b)为车轮通过凹坑后钢轨的Mises应力云图，从图7(b)可以明显看出凹坑对轮对造成的冲击反作用于钢轨而形成的应力增强区。

图7 钢轨凹坑处Mises应力云图(单位：MPa)

车轮通过之后钢轨的残余应力说明凹坑后方应力数值最大，为296.4 MPa。提取此时刻钢轨凹坑之后0.3 m内钢轨表面最大应力数值，绘制变化曲线，如图8所示，可以看出钢轨存在形成波浪形磨耗的趋势，危及行车安全。

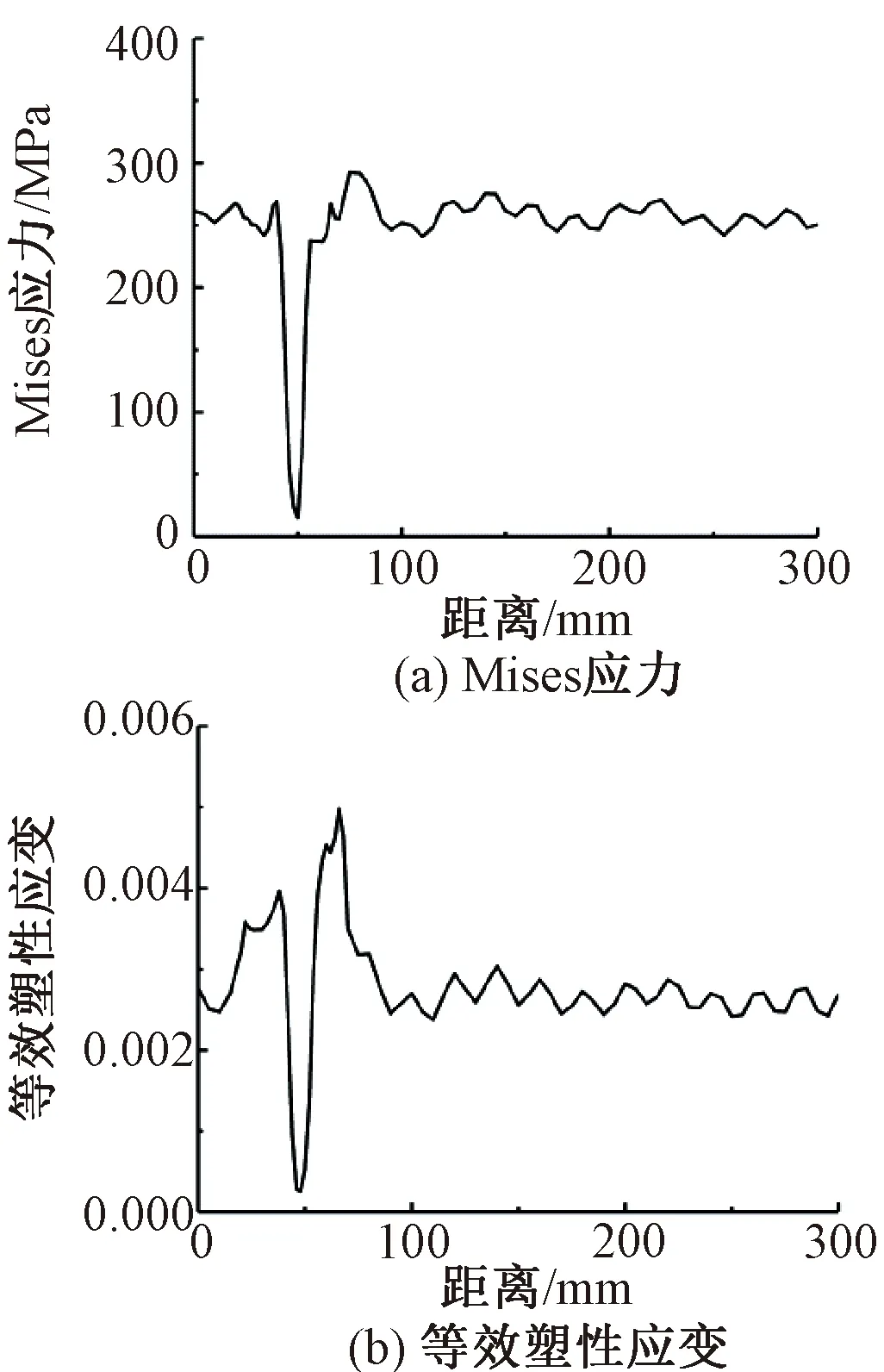
图8 0.08 s时钢轨凹坑附近Mises应力与等效塑性应变变化曲线

从图8可以看出，0.08 s时钢轨表面残余Mises应力在钢轨凹坑处发生剧烈跳动，且钢轨表面等效塑性应变也存在剧烈跳动，且二者发生区域相对一致。凹坑中心位置应力及等效塑性应变偏小，而凹坑后方(离开凹坑处)应力与等效塑性应变偏大，应力达到296.4 MPa，而等效塑性应变为0.005，与凹坑后方普通廓型钢轨的等效塑性应变0.002 8相比，近似增大一倍，且存在波浪形式。凹坑中心处等小塑性应变最小，两侧应力数值最大，说明钢轨凹坑存在进一步扩大趋势。并且从图8(b)可以看出，凹坑后等效塑性应变比凹坑前大0.001，所以凹坑后的扩大速度要高于凹坑前。

3 结论

本文采用Abaqus有限元分析软件建立轮轨高速滚动有限元模型，采用双轮计算模型，计算车轮通过钢轨凹坑的动力学响应，得到以下结论：

(1)在本文的计算条件下，钢轨凹坑会对高速通过的车轮造成振动冲击，使得轮轨力从稳定的60 kN突变至20 kN，随即升高至80 kN。并在之后的短时间内轮轨力处于波浪形变化过程。在此过程中变化的轮轨力会对钢轨和车轮造成不均匀的磨耗，容易引发其他病害。

(2)从轴箱垂向加速度可知，钢轨经过凹坑后会产生10g的冲击，主要集中在976.6 Hz。此冲击存在时间为0.01 s，即车轮经过凹坑之后的0.42 m距离内。车轮运行速度为150 km/h，976.6 Hz对应的波长为42.67 mm，故钢轨凹坑之后0.42 m距离内容易形成波长为42.67 mm的波浪形磨耗。由此可以看出钢轨凹坑与钢轨波磨存在一定联系。

(3)从Mises应力云图可以看出，车轮经过钢轨凹坑瞬间Mises应力为681.7 MPa，明显高于此次计算中稳定轮轨接触时的550 MPa。而在车轮通过凹坑后，钢轨表面残余应力变化曲线表明钢轨凹坑中心应力最小，凹坑边缘应力最大。同样，凹坑后边缘等效塑性应变最大，前边缘较小，但均大于轮轨正常接触时的数值。因此，钢轨凹坑有进一步扩大的趋势，且凹坑后扩大程度强于凹坑前。