考虑热效应和轮轨微观粗糙度的高速黏着机理数值分析
2020-02-01温泽峰金学松
吴 兵,陈 铭,吴 涛,温泽峰,金学松
(1. 苏州大学 轨道交通学院,江苏 苏州 215131;2.西南交通大学 牵引动力国家重点实验室,四川 成都 610031)
我国幅员辽阔,高速铁路营业里程已达到3.6万km。铁路系统是一个开放性系统,车辆在运行时轮轨系统基本暴露在外界环境中。轮轨界面不可避免的会受到如水、污油等液体“第三体”的污染。大量试验表明,此种工况极易引起低黏着现象的发生[1-2]。低黏着又对列车的牵引和制动产生较大的影响。黏着力不足,牵引时易产生空转,制动时易滑行,导致轮轨界面温度急剧升高,从而引起轮轨表面轮轨界面疲劳损伤[1]。因此,为了保障列车安全运营亟待从理论上获得轮轨间存在“第三体”时的黏着机理。
近几十年来,国内外大量的铁路工作者一直致力于轮轨黏着方面的研究,在试验和理论方面都取得了一些进展。文献[2-4]通过小比例双轮对滚试验机开展了一系列试验研究,获得了轮轨接触面干态、水介质、油污染等界面状态下的黏着特性。在试验中发现轮轨界面干态时,速度300 km/h以内对轮轨黏着力影响不大。试验结果也表明液体介质是影响轮轨黏着的主要因素。文献[5-8]通过小比例试验装置研究了轮轨间存在水、油、砂等“第三介质”时的黏着特性。文献[9]采用全比例高速轮轨滚振试验台开展了水、油污染物存在时的黏着试验,得到了高速条件下的黏着特性速度和蠕滑曲线。然而,理论建模和数值仿真的研究与试验研究相比较少。文献[10]建立了水介质存在时的二维简化黏着数值模型并调查了黏着特性。文献[11-12]利用平均流量理论获得轮轨黏着特性的二维和三维完全数值解。
现有数值模型并没有同时考虑轮轨表面粗糙度弹塑性接触行为、轮轨界面液体污染物的热效应及非牛顿效应的影响。而低黏着引起的空转和滑行导致的温升比较显著。本文建立考虑上述3个因素的二维轮轨黏着理论模型。通过多重网格技术求解该模型并开展一系列的膜厚分析,深入讨论表面粗糙度和热效应对轮轨黏着的影响机理。
1 高速轮轨黏着力模型
1.1 基本假设
(1) 由于轮轨椭圆接触的复杂性,将轮轨三维接触状态简化为二维问题。
(2) 假设轮、轨微观表面粗糙度高度为正态分布。
(3) 流体污染物与轮轨界面间无相对滑动并且和界面流体膜相邻的轮轨接触点的曲率半径远大于流体膜厚。
(4) 不考虑界面流体膜所受的流体压力和惯性力且流体压力沿着流体膜厚的方向保持不变。
1.2 模型描述
利用混合润滑理论和微观弹塑性固体接触理论,将界面流体热效应、微观固体弹塑性变形及非牛顿特性耦合到一个二维高速轮轨黏着特性数值的分析模型中,如图1所示。整个模型的求解分为压力场和温度场的求解。压力场计算模型的轮轨接触局部图如图1(a)所示。该模型将总载荷处理为由微观固体粗糙峰和界面流体共同承载。图1(b)为温度场的计算模型。本模型中温度的求解域包括车轮和钢轨与界面流体交界处、车轮和钢轨内部区域以及界面流体沿膜厚方向。
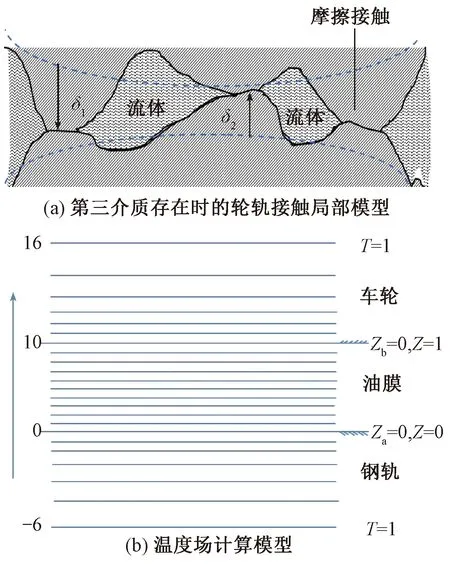
图1 高速轮轨黏着数值模型
1.3 无量纲基本方程
针对压力场求解过程中所选取的主要无量纲参考量如下:
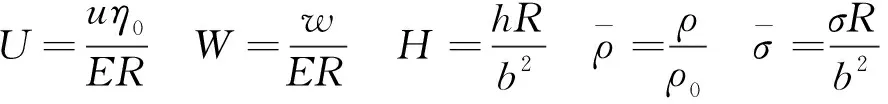
(1) 无量纲雷诺方程
在Patir和Cheng提出的用于混合润滑研究的平均流量模型的基础上,提出了能够求解同时考虑热效应和微观表面粗糙度的稳态二维线接触的一般Reynolds方程[13-14]。以无量纲形式可表示为
( 1 )
式中:
由式( 1 )可以看出,由于模型中考虑了界面流体的黏度和密度沿着膜厚的变化,式中出现了7个与界面流体黏度和密度相关的变量。σ为合成的轮轨微观表面粗糙度均方根值;η0和ρ0分别为界面流体的环境黏度和密度;u为轮轨接触点处的平均线速度;b为轮轨接触斑半宽;R为车轮的半径;H为名义膜厚,其定义基于图1中虚线轮廓;HT为局部膜厚,其定义基于实际微观粗糙面的轮廓。
如果微凸体合成高度δ的概率密度分布满足高斯分布,则HT可表示为

( 2 )
φx为x方向的压力流量因子[15]。
(3)
式中:c、r为常数;γ为粗糙度表面纹理参数。
φs为剪切流量因子[15]。
(2)密度方程
目前没有合适的经验公式用来描述水介质密度与压力、温度间的关系,因此本文采用描述润滑油密度方程的无量纲表达形式[13]。
( 4 )
式中:pH为最大赫兹接触压力;Dt=0.000 65T0,T0为环境温度。
(3)黏度方程
考虑到目前同样也没有能够描述水介质黏度与压力、温度关系的经验公式,因此本文应用考虑温度效应的Roelands关系式[13]。
( 5 )
式中:Z一般取0.6[13]。
(4)膜厚方程
( 6 )
式中:H0为无量纲中心膜厚;P和Pa分别为无量纲界面流体压力和微观固体粗糙度接触压力;Xin和Xout分别为进出口位置。
(5)载荷方程
由图1(b)可知轮轨力分别由轮轨表面微凸体和界面流体共同承载,其满足
( 7 )
在轮轨接触载荷作用下,接触斑内的微凸体可能发生塑性变形。本文采用能够考虑微观固体接触发生弹性、弹塑性及完全塑性变形的经验公式计算微观固体接触压力[16]。其无量纲表达式为
w*φ*(z*)dz*/pH
( 8 )

(6)温度方程
列车在高速和重载条件下运行时,轮轨接触界面可能会出现高应变率。而在此情况下,轮轨界面液体的流体特性极易发生改变。因此有必要考虑界面流体对轮轨黏着特性的影响。然而目前能够描述水介质流变特性的理论并未提出,因此本文讨论的界面流体均采用Ree-Erying非线性流变公式[17]。
( 9 )
式中:τ为流体剪应力;τ0为特征剪应力;η为Ree-Erying流体表观黏度,与Newton流体中定义的动力黏度是有区别的。
参考Newton流体的本构方程,引入等效黏度η*,其表达式为[13]
无量纲剪应力为
(10)
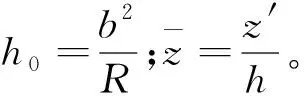

沿着z方向对式( 9 )积分求得速度场分布。
(11)
选取以下无量纲处理方法对温度场求解过程中的方程进行无量纲化。
流体能量方程为
(12)
相关参数可表示为
固体内部能量方程:
(13)
(14)
式中:CNa=bUcaρa/ka;CNb=bUcbρb/kb。
流体-固体界面热交换方程:
(15)
(16)
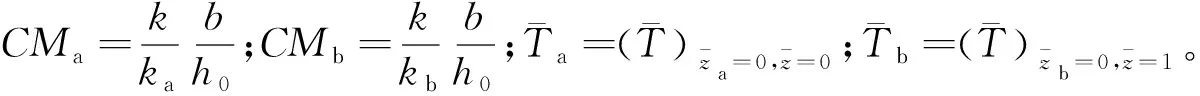
方程(1)~方程(16)组成了非线性较强的方程组,并在压力和温度计算域内进行数值离散,采用多重网格法求解上述方程[18]。本文使用了6层网格,最高层网格取为1 920。压力场和温度场交叉迭代求解获得微观固体和界面流体承载后,可得到轮轨间的黏着系数为
式中:FT为轮轨间的最大牵引力;μa为微观固体粗糙峰间的摩擦系数,本文参考文献[5]选取摩擦系数μa为0.45。
2 结果及讨论
由Stribeck曲线可知,当界面流体的膜厚比(Λ=h/σ)小于2时,固体承载比率增大,润滑状态由弹性流体动力润滑转化为混合润滑[19]。当润滑状态为混合润滑时,传统的摩擦副比如轴承、齿轮等为了研究其疲劳寿命都会将中心膜厚作为重要指标。针对轮轨摩擦副间存在流体润滑时的黏着特性的研究亦是如此。此外,由现有轮轨黏着理论研究结果可知微观固体承载与膜厚比Λ密切相关。由于考虑轮轨表面微观粗糙度,接触斑内的压力分布与Hertz压力分布和等温时的压力分布有较大区别[12]。因此,本文将讨论和比较考虑热效应和等温时粗糙度对膜厚的影响规律,同时调查速度和载荷对中心膜厚和固体承载比率的影响。由于水、油的相似性,此处主要以油污染为例进行讨论。
(1) 粗糙度对膜厚分布影响
图2给出了等温和考虑温度时界面流体膜厚在不同粗糙度等级时的分布。比较两种工况下的膜厚分布发现,粗糙度对膜厚分布的影响截然不同。等温时轮轨表面越粗糙膜厚数值越大,而膜厚比(Λ=h/σ)越小。这也解释了等温条件下增加表面粗糙度能够增黏的原因。从图2(b)发现考虑温度时,当σ< 5 μm时,膜厚随着表面粗糙度的增大而增加;而当粗糙度σ> 5 μm时,膜厚随表面粗糙度增大而减小。从图2可以看出无论等温还是考虑温度,膜厚比都是随着粗糙度的增大而减小,因此增大轮轨表面粗糙度都可以使得黏着系数增大。值得注意的是温度对膜厚数值影响较大,在相同工况下,等温时的膜厚数值比考虑温升的膜厚值大近10倍。

图2 速度200 km/h时不同粗糙度下的膜厚分布
(2) 粗糙度对压力分布影响
轮轨表面粗糙度不仅影响膜厚分布还关系到微观固体接触压力的分布。图3给出了4种不同粗糙度时考虑温度和等温时界面流体和微观固体接触压力分布。当表面粗糙度为2 μm时,微观固体压力几乎为零。微观固体接触压力随着粗糙度的增大逐渐增加,但数值相比于界面液体承载小得多。粗糙度对固体接触压力分布的影响也从理论上解释了表面越粗糙黏着力越大的原因。此外,图3还表明温度对于微观固体接触压力的分布有明显的影响。这个原因在前述粗糙度对膜厚比的影响中已经讨论过,图3也再次验证了以上的观点。

图3 等温和考虑温度情况下不同粗糙度压力分布规律(速度200 km/h)
(3) 接触压力和速度对中心膜厚和承载率的影响
由式( 8 )可见最大赫兹接触压力直接影响着微观固体粗糙峰的承载大小。为此,图4和图5分别调查了等温和考虑热效应两种情况下,不同表面粗糙程度时接触压力对中心膜厚和固体承载率的影响规律。图4表明无论是否考虑热效应,中心膜厚和膜厚比都随着接触压力的增大而减小,且中心膜厚减小幅度更大。从图4还可发现,随着压力的增大,考虑热效应的中心膜厚的减少幅度比等温时大,这也从另一个方面说明考虑热效应的必要性。从图5可以看出,固体粗糙峰承载率在等温工况下随接触压力的增大而下降。而考虑热效应时的变化规律则与表面粗糙度程度有关。与图2中膜厚分布类似,当σ>5 μm时,固体承载率变化规律与等温时一致。当σ<5 μm时,固体承载率则随着接触压力的增大而减小。其原因可由图4看出,σ<5 μm时的中心膜厚较其他粗糙度大,从而在同一载荷下不易引起塑性变形,以弹性变形为主,而粗糙度较大时则以弹性和塑性变形为主,所以随着接触压力增大其实际固体载荷相对增加量较大,因此固体承载率增大。图5也表明在同一粗糙度时,考虑热效应的固体承载率较等温时大。图4中虽然膜厚比和中心膜厚都随着接触压力的增大而减小,即固体承载力会增大,但是图5结果表明由接触压力的增加而引起的固体承载力的增量比总载荷的增加量小,因此固体承载率(La)下降。上述结果表明温度对轮轨接触的影响不可忽略,在数值模型中应加以考虑。

图4 接触压力对中心膜厚的影响(速度200 km/h)
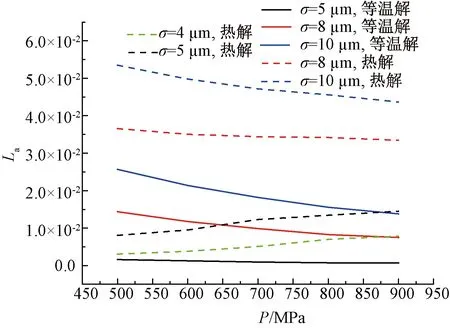
图5 接触压力对承载率的影响(速度200 km/h)
图6和图7分别调查了等温和考虑温升两种工况下,不同表面粗糙度时速度对中心膜厚和固体承载率的影响。从图6可以看出,两种工况中心膜厚和膜厚比都随速度的升高而增加。在同一表面粗糙度下,考虑温度时的中心膜厚比等温时的小。图7表明两种工况下随着速度的增加固体承载率减小。结合图6和图7可以发现,中心膜厚越大,固体承载率越小,且等温时的固体承载率比考虑温升时要小。这也说明了温度的考虑是有必要的。
(4) 接触压力和速度对温度的影响
图8和图9分别为接触压力和速度对液体中层温度分布的影响。图8分别选取了500、700、900 MPa 3种接触压力,获得了速度为200 km/h时的温度分布情况。从图8可以发现,随着接触压力的增大,无量纲中层温度也相应增大,且各接触压力下温度峰值相差较大。然而,温度在入口和出口区域的变化规律与接触中心区域相反。从图9可以看出,在整个求解区内无量纲中层温度的峰值随着速度的增加而升高。综合图8、图9结果还可以发现,速度和接触压力对中层温度的影响均较大,而由图4结果可知温度对膜厚影响较大,因此在模型中必须考虑温度的影响。
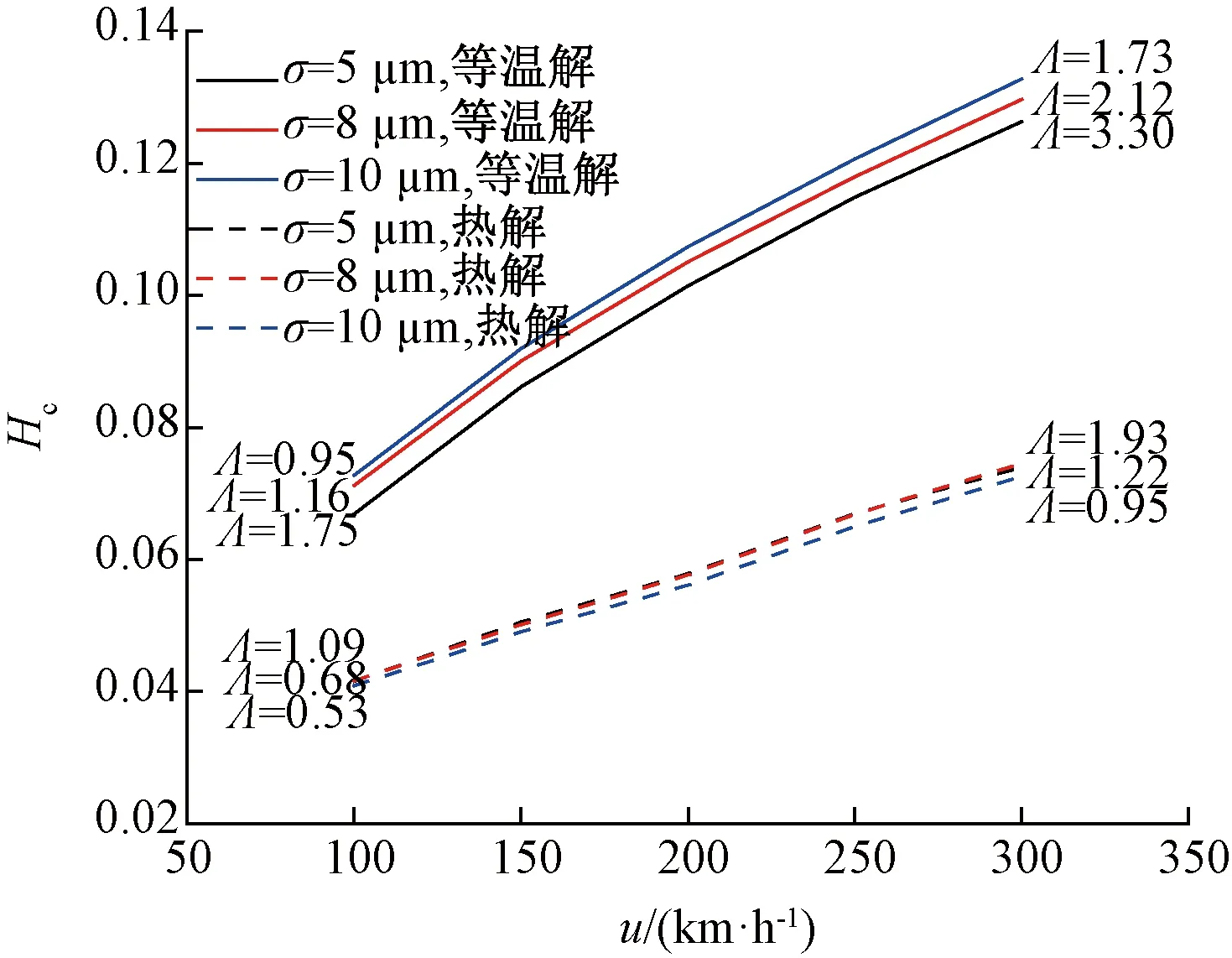
图6 速度对中心膜厚的影响

图7 速度对承载率的影响
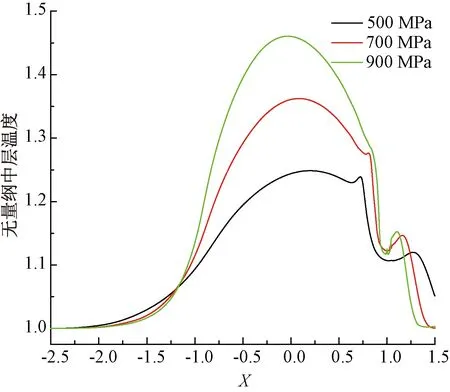
图8 接触压力对温度的影响(u=200 km/h,σ=5 μm)

图9 速度对温度的影响(pH=768 MPa,σ=5 μm)
3 速度对黏着系数的影响
列车运行速度一直是制约高速铁路进一步发展的重要因素。从上述讨论的速度对中心膜厚和固体承载率的影响表明速度是影响轮轨间黏着系数的关键因素之一。大量国内外研究结果表明,轮轨界面存在液体污染物时,列车速度对轮轨黏着特性影响显著[1,8-9,11]。因此本文重点讨论了轮轨间存在水、油两种界面污染物时速度对黏着系数的影响规律。
选取CRH2型动车组踏面的几何与载荷参数作为数值模型输入量,并考虑微观固体粗糙峰的弹塑性变形和界面流体热效应等因素,在获得接触机理后,得出了速度对轮轨黏着特性的影响结果,如图10所示。从图10可以发现,对于水、油两种界面污染,随着速度的增加轮轨间黏着系数急剧下降。其原因是轮轨间液体膜厚随着速度的增加而变大,使得固体粗糙峰承载变小,所以导致轮轨间的黏着系数减小。这种变化规律可由上述膜厚分析解释。此外,图10结果还表明在同一计算工况下,相比于水介质,轮轨间存在油污染时更易导致低黏着现象的发生。这是由于水的黏度比油小,使得水膜厚度比油膜厚度小,继而使得其固体承载比油污染时大。大量文献的研究结果也表明应用此模型计算的黏着系数的变化规律与实验结果一致[9]。

图10 水、油介质存在时速度对黏着系数的影响
4 结论
本文建立一个能够考虑热效应、轮轨表面微观粗糙度弹塑性变形及界面流体非牛顿效应的二维轮轨黏着数值模型,研究轮轨间存在液体污染物时表面粗糙度、接触压力及界面流体热效应对轮轨接触特性影响的机理。讨论水和油两种界面污染物时黏着系数随速度的变化规律。得到以下结论:
(1) 通过膜厚分析发现轮轨表面粗糙度、界面流体热效应、列车速度及接触压力对膜厚、膜厚比及固体承载率影响显著。此外,在对考虑温度的模型进行膜厚分析时发现,针对本文的计算工况,粗糙度为5 μm时为分界点,当σ>5 μm时膜厚随着粗糙度增大而减小,σ<5 μm时膜厚随粗糙度减小而减小。
(2) 轮轨间有水、油存在时,黏着系数随列车速度的增加而显著降低。所以在列车高速运行时,遇到界面流体污染物时,需在某些特定环境情况下使用增黏技术,以确保列车的高速正常安全运行。
