当学生会背诵乘法口诀时，教师怎么教？

邵燕

[摘要]教学乘法口诀时经常会遇到大部分学生通过预习就已经会背诵的情况。这时教师应改变教学方法，从学生的角度出发，让教学更贴近学生，启发学生真正理解和把握口诀的内涵与意义，挖掘口诀中的规律，体会口诀的价值。

[关键词]乘法口诀;体验;口诀;备课;以生为本;换位思考

[中图分类号]G623.5

[文献标识码]A

[文章编号]1007-9068（2020）32-0050-02

大部分学生在正式学习乘法口诀前已经会背诵1～9的口诀了。问题也就此产生：学生已经会背诵了，课堂上再教岂不是画蛇添足？

有教师认为，就算是学生能背诵口诀，但也是机械性记忆，对于口诀的内涵其实似懂非懂，没有做到心领神会。这位教师一语中的，大多数学生背诵乘法口诀是一种条件反射，口诀就类似一个语段一样被记取。基于此，乘法口诀的教学重点可以这样确立：促使学生从对口诀的机械性复读到智能性复述转型。

一、改弦更张，重在体验与领会

既然学生已经会背诵口诀，那么课堂上再让学生尝试编创口诀就毫无意义。此时最该做的是把学生的精力和视线导引到口诀本身的内涵和意义上。与此同时，诱导学生从口诀特征上探究，让学生对乘法口诀的认知达到形式与内涵的统一、口诀与心法的统一。

如“7的乘法口诀”教学实录节选：

师：大家看一看，老师手中拿的是什么？（纸鹤）大家会折纸鹤吗？请看大屏幕，（出示情境图）对折纸艺术情有独钟的聪聪正在跟同伴学习折纸鹤呢！请仔细看图，你能提取哪些数学信息？

生1：每人折了7只纸鹤。

生2：一共有7个小朋友。

师：你能设计一个数学问题吗？

生3：一共折了多少只纸鹤？

师：老师也有许多待解的问题，大家愿意助我一臂之力吗？

师：每位折纸爱好者折7只纸鹤，那2位折纸爱好者一共折几只纸鹤？3位折纸爱好者一共折几只？4位、5位、6位、7位折纸爱好者各折几只纸鹤呢？

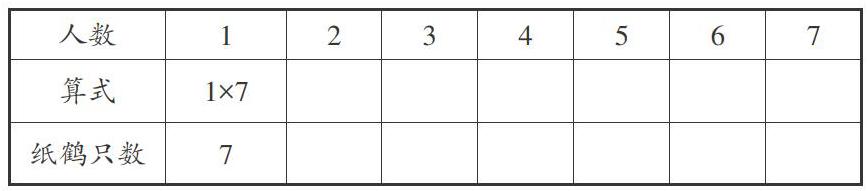
师：问题有点杂乱，我们来整理一下。1位折纸爱好者折7只纸鹤，也就是1个7，列算式为1×7。（填入表格）

师：同桌两人结对子，将这些问题一一击破吧。

师：求2位折纸爱好者一共折了几只纸鹤，为什么要用2×7呢？

生4：2位折纸爱好者折的纸鹤总数是2个7，所以是2×7。

师：那6位折纸爱好者一共折几只纸鹤？

生5：6个7，也就是6×7。

师：对，有几个7就用几乘7。依我看，这个表格大有名堂，里面的数据排列是有规律可循的。你察觉到了吗？

生6：可变乘数是按照1、2、3……的自然数顺序变化的。

生7：算式是按照1×7、2×7、3×7……的顺序排的。

师：这样有规律地依次排开，我们一眼就能看出得数。那如果随机抽查，突袭式地问你4位折纸爱好者一共折几只纸鹤，你能很快答出来吗？

生8：4×7=28。

师：你是怎么快速判断出是4×7=28的？

生8：可以用口诀，四七二十八。

师：你们都背熟了口诀吗？能将刚才的表格完善一下，补充口诀这一栏吗？

生（齐）：……

师：看来大家早已对7的口诀倒背如流。你觉得哪几句口诀记忆犹新？（提醒学生完整表述：我对……记忆犹新）你对哪几句口诀非常容易忘记？谁有巧记法，能速记这些口诀？（学生一时语塞）

师：许多数学知识都是有规律的，如果能够查明这些规律，我们学起数学就会事半功倍。7的乘法口诀就是一例，我们一起来验证一下。

（启发学生说出：口诀的首位数字依次是1、2、3、4、5、6、7，第2个数字都是7）

师：总而言之，口诀首位数字依次是1～7，一七，二七，三七，四七，五七，六七，七七。再来观察口诀的乘积，又有什么规律？

（启发学生说出：从上往下看，乘积逐次多7;从下往上看，乘积逐次少7）

以上教学实录，教师充分尊重学生已经会背乘法口诀这个既定事实，巧妙地将口诀与解决实际问题交织起来，既让学生体会到口诀的实用价值，又使学生挖掘出口诀中的数学规律。

二、革除备课陋规，更加贴近学生

尽管“生本位”的理念已被推广，但教师仍习惯性地越俎代庖，喜欢围绕着重点知识用尽手段，诸如创设情境、组织研究、设计练习题，而无暇顾及对学生的学习方法和学科素养的培养。这种陋习也是需要革新的，最基本的就是对学生的起点和近况详细分析。例如，教学“两、三位数除以一位数”时，遇到商中间有0的除法计算时，不妨事先分析学生是否已经精通两、三位数除以一位数的一般除法计算，如估算试商、会对齐商的位置，如果学生已经掌握，重点就应转移到“商中间为何冒出0”的缘由上。

对于经验欠缺的新教师来讲，一方面整个小学知识框架还未建立，另一方面对学生的生活环境和学习情况知之甚少，这个时候要摸清学生的底细，最有效的方法就是课前调研访谈。如要确定“两位数除以一位数”的教学设计思路时，在没有任何背景资料的情况下，可深入班级考察，出示52÷4，让学生现场解答。统计结果显示，70%的学生束手无策;10%的学生运用逆向思维——乘法，4×9=36，4×10=40，4×11=44，4×12=48，4×13=52;20%的學生列了除法竖式，但商9后就卡壳了。有了这个第一手资料，就可以分析得出，教学“两、三位数除以一位数”的笔算前，学生只有表内除法的基础，教师备课时就能量体裁衣。

三、换位思考，将心比心才能读懂学生

在实际的备课中，不妨“客串”一下学生角色，换位思考：“如果换作是我，我会怎样想？”设想学生的正常思路和可能遇到的困惑。如小数点的位置移动引起小数大小的变化规律，将心比心想一想：“小数点怎么移动？小数值怎么随之变化？有何规律？”在具体的研究中，又思考：“小数点如何位移才算向左移动一位、两位？凭什么小数点向左移动就是缩小，向右移动就是扩大？为什么每移动一位引起的数值大小变动就是10倍、两位就是100倍……”对这些问题的深思可以为确立重难点提供依据和佐证。

应该说，对某节课的评析甚至比授课本身还要精彩，而最精彩的应该是对教师观念的洗礼和冲击，如果能由一节课的改变而让教师认定一个新的先进理念，那才是善莫大焉。

（责编 吴美玲）