严格α-对角占优矩阵线性互补问题的误差界

李艳艳

（文山学院 数学与工程学院，云南 文山 663099）

由于期权定价问题、最优停步问题等均可以转换为线性互补问题，所以线性互补问题解的误差估计，得到了许多学者的关注和研究。

线性互补问题（Lcp (A，q)）的模型是指求x∈Rn，满足

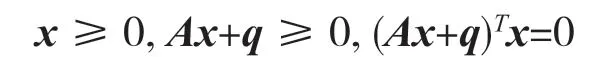
其中A是实矩阵，q是实向量。

2006年，陈小君等在文献[1]中给出了当矩阵A是主子式都为正的实矩阵（P矩阵）时线性互补的误差界

本文研究目前较少被关注的严格α-对角占优矩阵线性互补问题的误差界估计问题。

1 预备知识

为了后面研究的需要，首先引入一些记号：

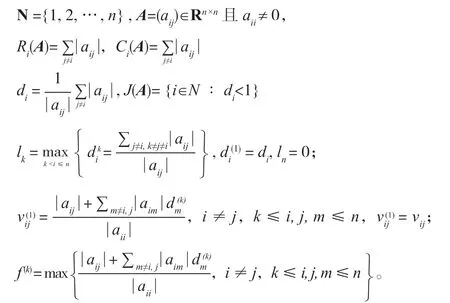
定义 1[7]设A=(aij)∈Rn×n，若存在α∈[0,1]，使得

＞αRi(A) + (1-α)Ci(A)成立，则称A为严格α-对角占优矩阵。

定义 2[8]设A=(aij)∈Rn×n，若 ∀i，j∈N，都有aij≥ 0，则称A为非负矩阵，记为A≥ 0。

定义3[9]设A=(aij)∈Rn×n，当i≠j时，aij≤0，且A-1≥0，则称A为非奇异M-矩阵。

引理 1[10]设A=(aij)∈Rn×n为严格对角占优矩阵，则

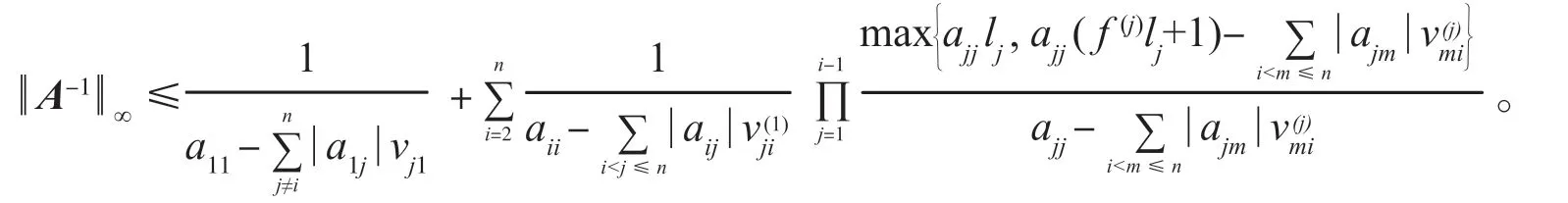
引理2[11]若

引理3[12]设A=(aij)∈Rn×n为严格α-对角占优矩阵，则称A是H-矩阵。

引理 4[13]设γ＞ 0，η≥ 0，则对 ∀x∈ [0,1]，

引理 5[14]设A=(aij)∈Rn×n满足则对任意的xi∈[0,1]，i∈N，有

2 主要结果

这部分，首先给出严格对角占优矩阵线性互补问题的误差界，其次利用该误差界，通过把严格α-对角占优矩阵分裂成严格对角占优矩阵和对角矩阵，得到了严格α-对角占优矩阵线性互补问题的新误差界。

B+是Z矩阵(非主对角元素非正的矩阵)，C是非负矩阵。

定理1设A=(aij)∈Rn×n是对角元素为正的严格对角占优矩阵，可表示为A=B++C，其中B+=(bij)，则

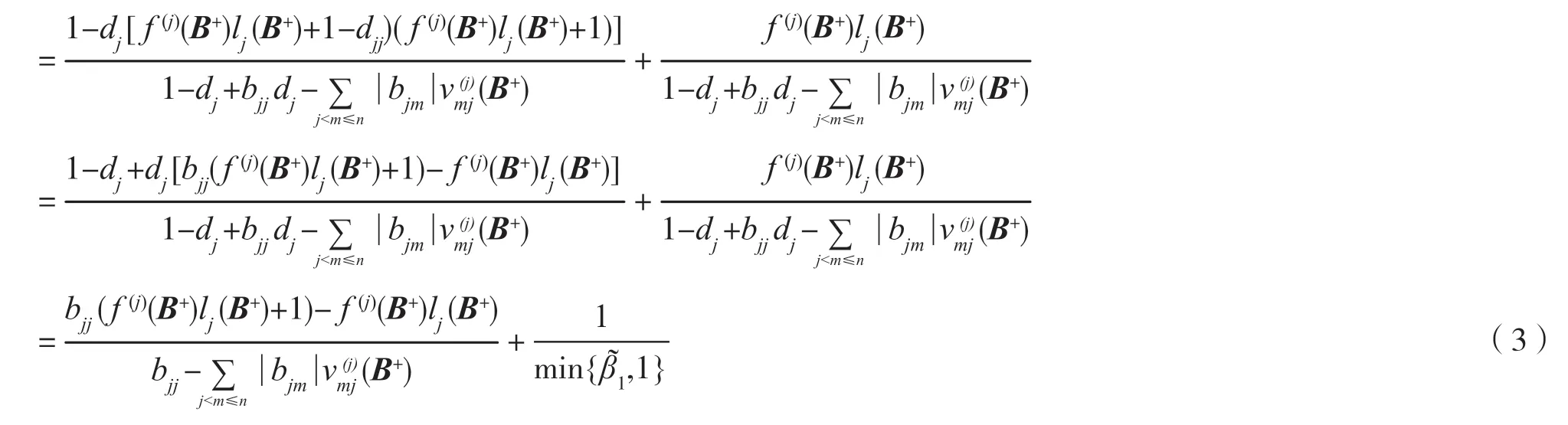
结合（1）～（3）式得

下面利用定理1的结果，通过对严格α-对角占优矩阵进行分裂，得到该矩阵线性互补问题的误差界。

定理 2设A=(aij)∈Rn×n为严格α-对角占优矩阵，α∈[0，1]，

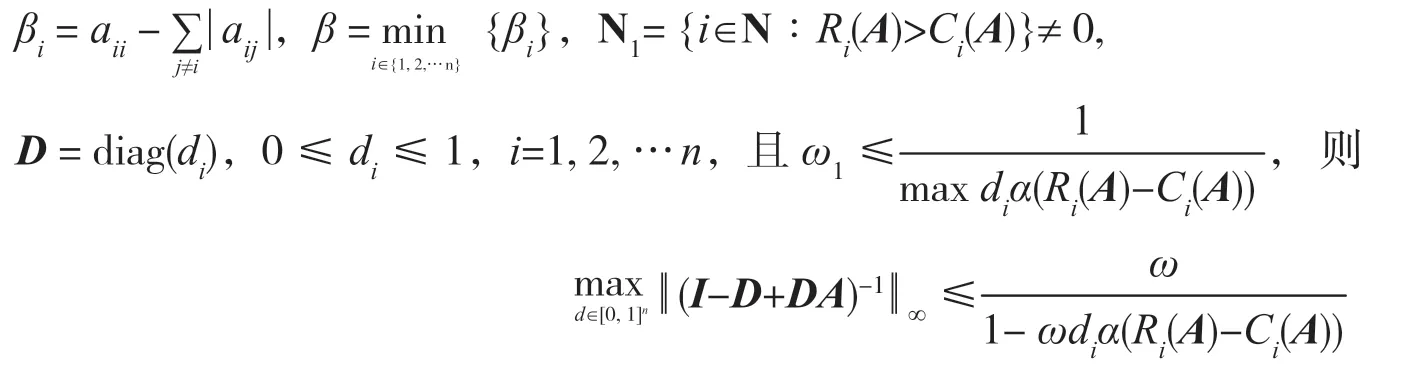
证明：令A=B-F，其中B=(bij)，F=(fij)，且

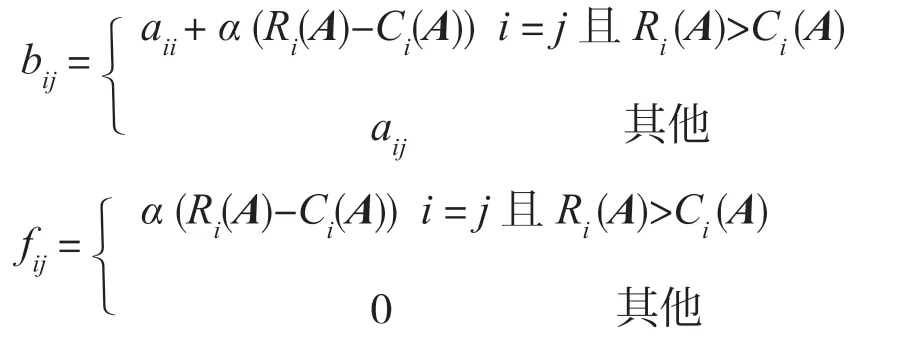
因为A=(aij)∈Rn×n为严格α-对角占优矩阵，所以

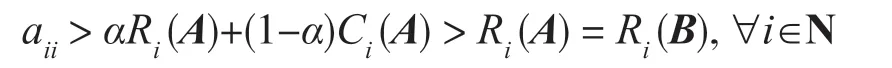
若i∈N1，则bii=aii+α(Ri(A)-Ci(A))+(1-α)＞Ri(A)=Ri(B)

若i∉N1，则bii=aii+Ri(A)+α(Ri(A)-Ci(A))＞Ri(A)=Ri(B)

则B是严格对角占优矩阵，令

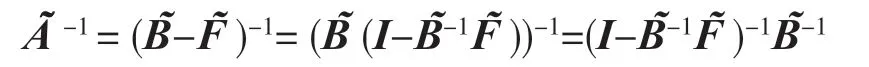
因此

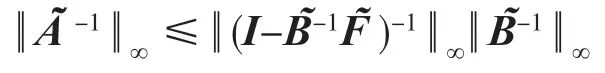
因为是严格对角占优矩阵，由定理1知

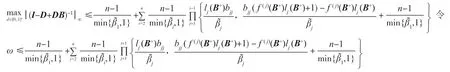
下面证明

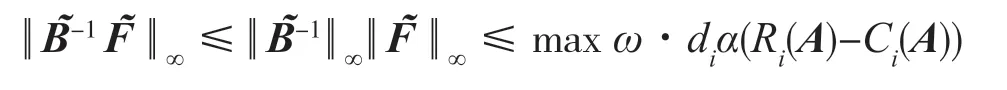
由引理2知

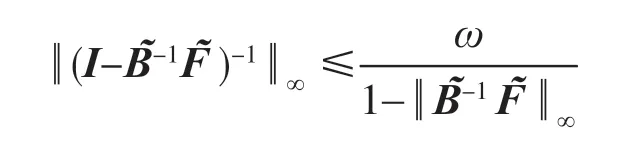
由以上证明知

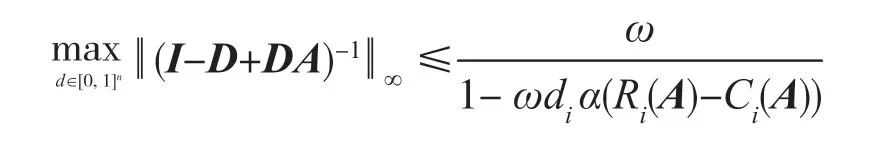
定理证毕。

3 数值算例

通过该例说明，本文估计式一定程度上提高了文献[14]中的相应结果。