新的NTRU格上抗量子攻击的群签名方案

叶 青，杨晓孟，秦攀科，赵宗渠，汤永利

河南理工大学 计算机科学与技术学院，河南 焦作454000

1 引言

1991 年，Chaum 和Heyst[1]提出了群签名的概念，并构建了第一个群签名方案。在群签名中，有多个成员，其中每个成员都可以代表群体进行签名，验证者可以通过系统公钥验证签名是否合法，但无法确定具体是哪个用户执行了签名，发生争议时可由群管理员通过追踪密钥找到签名者的身份。随后文献[2-3]对文献[1]进行了改进，使方案效率提升且更具有实用性。但以上群签名方案的共同特点是基于传统的数论难题（例如：大整数分解问题、离散对数问题和椭圆曲线问题）构建，而在量子计算机得到应用的前提下，传统基于数论难题构建的群签名方案都将在多项式时间内被破解，因而，研究抗量子攻击的群签名方案成为该领域亟待解决的问题。近几年，基于格理论构造的签名方案[4-5]和加密方案[6-7]因具有运算效率高、计算可并行化、抗量子攻击和存在最坏情况下的随机实例等优点，成为后量子密码时代的研究热点。

2010年，Gordon等[8]在ASIACRYPT'10提出了第一个基于格的群签名方案（简称GKV2010 方案），该方案首先用Gentry等[9]中的格上签名方案对消息进行签名得到签名e，然后基于Regev[10]的格上加密方案使用系统公钥对签名e 进行加密得到密文c，最后构造了一个非交互式证据不可区分（Non-Interactive Witness Indistinguishable，NIWI）的证明，证明密文c 是通过系统公钥对签名e 进行加密得到的，该方案签名长度为O(N)（其中N 为群成员的个数）。2013年，Laguillaumie等[11]在ASIACRYPT'13 提出了第一个签名大小为O(lb N)的格上群签名方案。2015年，Nguyen等[12]在PKC'15提出了更加简单高效且签名长度同样为O(lb N)的格上群签名方案。Kawachi 等[13]在ASIACRYPT'08 上首次将零知识证明与格上SVP 困难问题相结合提出了格上并发安全的认证方案。在零知识证明系统中，证明者可以在不向验证者提供任何有用信息的情况下，而使验证者相信某个论断是正确的，零知识证明的这种特性使得它在构造密码方案的匿名性方面可以发挥重要作用。随后，Ling 等[14]在PKC'13 上基于SIS 难题和LWE 难题使零知识证明能够处理矩阵-向量关系，于是零知识证明进一步被用于构造格上密码方案[15-17]。

近几年，基于格的群签名方案成果很多[15-19]，但是都有通信代价高、系统公钥尺寸过大的弱点，而NRTU格是一类基于多项式环的特殊格，因在其计算过程中只涉及到多项式环上的乘法和小整数求模运算，与一般格相比较，NTRU 格密码体制所需的公私钥长度更短，运算速度更快。本文依据GKV2010群签名方案“签名-加密-NIWI 证明”的构造思路，采用Ducas 等[20]在ASIACRYPT'14 提出的NTRU 格上高效参数生成的算法（简称DLP算法），构造了一个基于NTRU格的群签名方案。在本文方案中，首先采用DLP算法产生NTRU格上群签名的系统公钥、追踪密钥和用户签名密钥，然后用Hoffstein等[21]提出的NTRUSign签名算法对消息进行签名得到签名e，再用文献[22]提出的NTRUEncrypt 加密算法使用系统公钥对签名e 进行加密得到密文c，最后基于NIWI 证明[8]来证明密文c 是系统公钥对签名e 进行加密得到的。在GKV2010 方案的安全模型下，基于LWE困难问题证明本文的NTRU 格上群签名方案满足匿名性，基于近似CVP 困难问题证明所提群签名方案满足可追踪性。

2 符号介绍

表1对下文中出现的符号进行说明。

表1 符号介绍

除了表1 中的符号，文中还用到O ，O~ 等符号，为常用计算复杂度符号。

3 预备知识

3.1 NTRU格的相关定义

定义1（格）设b1,b2,…,bm是n 维欧式空间ℝn上m 个线性无关向量，格定义为所有这些向量的整系数线性组合，即，其中，向量组b1,b2,…,bm称为格Λ 的一组基。

定义2（q 元格）设q,n,m ∈ℤ,A ∈,且u ∈满足Ax=u mod q。定义：

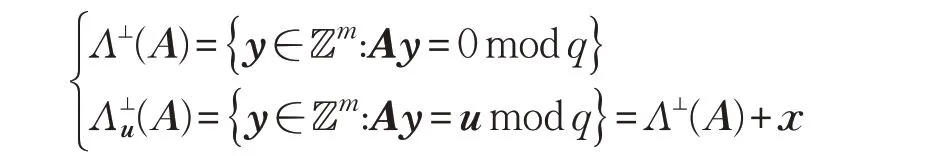
定义3（NTRU 格）令n,q ∈ℤ+，多项式f、g、F、G ∈R 满足f*G-g*F=q，由f、g、F、G 生成的NTRU格是指以矩阵的行向量作为格基生成的格，其中，A(x)表示多项式x 所对应的卷积多项式。

定义4（离散高斯分布）对任意σ ＞0，定义以向量c为中心，σ 为参数的格Λ 上离散高斯分布为：

其中有x ∈Λ,ρσ,c(x)=e

3.2 困难问题假设

定义5（最近向量问题（Closest Vector Problem，CVP））求出格中与某一个给定向量距离最短的向量，即任意给出一个点p，格L 中与点p 距离最近的向量称之为最近向量。格L 与点p 的距离记为λ1(p,L)，同样地，格L中与点p 距离次近的向量与p 的距离记为λ2(p,L)，以此类推，那么有：

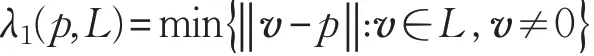
可以证明，在p 范数(p ≥1)的形式下，CVP 是NP难题。

近似最近向量问题（Approximate Closest Vector Problem，Appr-CVP）：某个算法对于输入的格L 和任意的目标向量p 可以找到格L 中距离p 不超过cλ1(p,L)的非零格向量v(v ∈L)（c 为近似因子，是格中某个量的函数），可称该算法以因子c 近似解决CVP。已经证明：具有小因子c 的近似最近向量问题（Appr-CVP）是NP难题。

定义6（判定性容错学习（Decisional Learning With Errors，DLWE）问题）给定正整数n，整数m ≥n 和q ≥2及向量s，一个ℝm上的概率分布χ 。定义两种在×[0,q)m上的分布：

（1）LWEm,q,χ(s)：选取中均匀分布的矩阵A，进行抽样得到e ←χ，然后输出(A,ATs+e)。

（2）Um,q：选取中均匀分布的矩阵A 与[0,q)m中均匀分布的向量y，然后输出(A,y)。

判定性LWE 问题即为：区分LWEm,q,χ(s)和Um,q。假设存在概率多项式时间算法时间D，可以得出Pr[s ←；(A,y)←LWEm,q,χ(s):D(A,y)=1]=1-Pr[(A,y)←Um,q:D(A,y)=1]是可忽略的，那么DLWEm,q,χ(s)是困难的。

本文方案基于DLWE难题，由于分布χ 取自离散高斯分布Dℤm,αq,所以判定性LWE问题表示为DLWEm,q,α。

3.3 非交互证据不可区分（Non-Interactive Witness Indistinguishable，NIWI）证明

文献[8]给出了非交互证据不可区分的证明系统，定义如下。

首先定义判定语言Ls,γ：

以下为两种等价情况：

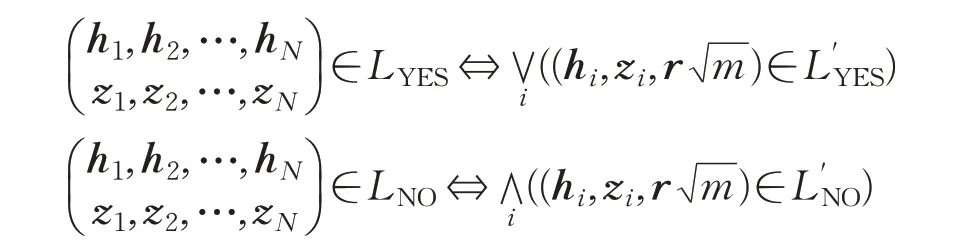
引理1[8]当时，在随机预言模型下，对于Ls,γ，存在一个对的非交互式不可区分的证明系统，该系统长度为O(mnN lb q)bit。

4 NTRU格上相关算法的介绍

4.1 NTRUEncrypt算法

密钥选取。首先定义p,q 为整数，满足gcd(p,q)=1,其中q ＞p。在多项式环R=ℤ[x]/(xn-1)中，随机选取两个多项式f,g，次数均为N-1，系数为整数。多项式f 满足模p 和模q 都有逆，分别记为fp,fq，即：

fp*f=1(mod p),fq*f=1(mod q)

计算h=pfq*g(mod q) ，上述式子中的mod p 和mod q 是指多项式的系数分别是区间中的整数。那么有公钥pk=h，私钥sk=(f,fp)。

加密。消息m 为多项式，次数为N-1，系数为整数。随机选取一个多项式r ，次数也为N-1，系数为整数。计算：c=r*h+m(mod q)。

解密。首先计算a=f*c(mod q)，其中a 的系数属于集合。然后计算m=Fq*a(mod q)。

4.2 NTRUSign算法

密钥选取。首先定义β 为平衡因子，其范围为0 ＜β ≤1，NormBound 为验证签名是否合法的临界值。在多项式环R=Z[x]/(xn-1)中，随机选择两个小多项式f,g，满足模q 有逆。计算多项式(F,G)满足：

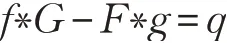
在Rq上对f 进行求逆运算生成fq，在Rq上对g进行求逆运算生成gq，那么公钥为h=F*fq(mod q)，私钥为(f,g)。

签名。对消息B 使用hash 变换：H(B)，得到消息摘要m ∈[0,q)N。进行如下计算：

其中{ }x 表示{ }x =x-round(x)。

输出签名：s=ϵfj+ϵ′gj。

验证。对消息B 使用hash 变换：H(B)，得到消息摘要m ∈[0,q)N。首先计算t=s*h mod q，然后计算规范数：

如果有v ＜Normbound ，则表示验证成功，否则，表示验证失败。

5 群签名及安全模型

一个群签名方案[1，8，11-12，15-18]G 一般包括以下四个基本算法：

（1）密钥生成算法（G.KeyGen）：输入安全参数λ，输出群公钥PK ，用户私钥gsk 和追踪密钥TK 。

（2）签名生成算法（G.Sign）：输入消息M 和用户私钥gsk，输出对消息的签名σ。

（3）签名验证算法（G.Verify）：输入消息M ，对消息的签名σ 和群公钥PK，验证成功输出1，验证失败输出0。

（4）签名打开算法（G.Open）：输入对消息的签名σ，消息M 和追踪密钥TK ，输出签名者身份i。

Gordon 等[8]在ASIACRYPT'10 提出了第一个格上群签名并给出了具体的安全模型，即群签名应满足正确性，匿名性和可追踪性。2015年，Nguyen等[16]在该安全模型下证明了PKC'15 上提出的签名长度为O(lb n)的格上群签名方案的安全性，Libert 等[17]同样在该安全模型下证明了EUROCRYPT'16提出的不需要陷门的格上群签名方案的安全性，因此，本文方案也采用该安全模型[8]，定义如下：

定义7（正确性）一个合法的签名，必然能通过签名验证算法的检验并且群管理员可推导出该签名对应的用户身份。即：对于G.KeyGen 生成的(PK,TK,gsk)，任意消息M 和任意用户i，如果签名为σ ←G.Sign(gsk[i],M)，那么必然可以得到：

G.Verify(PK,M,σ)=1；G.Open(TK,M,σ)=i

定义8（匿名性）匿名性是指，在没有追踪密钥的情况下，即使给出所有用户的签名密钥，也推断不出具体是哪个群成员对消息进行了签名。即：一个群签名方案G具有匿名性，那么对于任意概率多项式时间敌手在下列游戏中获胜的优势是可忽略的：

（1）挑战者运行G.KeyGen ，并将公钥PK 发送给敌手A。

（2）敌手A输出两个ID:i0,i1∈[N]以及消息M 。挑战者随机选择比特b，并将群签名G.Sign(gsk[ib],M)发送给敌手A。

（3）敌手A经过一系列的询问后输出b′。

定义9（可追踪性）可追踪性是指群管理员可以通过追踪密钥找到正确签名者的身份。即：一个群签名方案G具有可追踪性，那么对于任意概率多项式时间敌手在下列游戏中获胜的优势是可忽略的：

（1）挑战者运行G.KeyGen ，并将公钥PK 和TK发送给敌手A。

（2）敌手A可适应性地进行如下的预言机询问：

①敌手A可询问私钥预言机，对于输入i，输出SKi。

②敌手A可询问私钥预言机，对于输入i,M ，输出G.Sign(SKi,M)。

（3）经过一系列询问后，A 输出一个消息M 和签名σ ，设C 为A对私钥预言机进行过询问的i 的集合。如果以下三个条件均成立，则称A获胜。

①G.Verify(PK,M,σ)=1；

②对于i ∉C,A 未进行G.Sign(i,M)的询问；

③G.Open(TK,M,σ)∉C 均成立。

6 本文的方案

本文方案依据GKV2010 方案“签名-加密-NIWI 证明”的构造思路，但与GKV2010 方案的不同之处在于，密钥生成算法采用DLP算法[20]产生系统公钥、追踪密钥以及用户签名密钥；签名生成算法，首先采用NTRUSign 算法[21]对消息进行签名得到签名e ，然后基于NTRUEncrypt 算法[22]用系统公钥对签名e 进行加密得到密文c，最后基于一个NIWI 证明[8]，证明密文c 是系统公钥对签名e 进行加密得到的；签名验证算法基于NTRUSign算法的签名验证算法。方案具体构造如下。

6.1 密钥生成算法

设λ 为安全参数，N 为群签名中用户个数（其中N=2l），令大模数q=poly(λ)，小模数p=negl(λ)，维数为n 。对于一个f ∈R′ ，定义为R′ 中满足条件的特殊多项式，如果那么有

密钥生成算法具体如下：

（2）根据欧几里德算法，计算rf、rg∈R,Rf、Rg∈ℤ,并且满足rff=Rfmod(xn+1) 和rgg=Rgmod(xn+1)（如果GCD(Rf,Rg)≠1或GCD(Rf,q)≠1则返回上一步）。

（3）计算tf、tg∈ℤ，使tfRf+tgRg=1。然后计算：

再根据计算得到的F′,G′,k 计算：F=F′′-K*f ，G=G′-k*g。

（4）在Rq上对f 进行求逆运算生成fq，在Rp上对f 进行求逆运算生成fp，即进行运算和

那么群成员的签名密钥为(f,g)。计算群成员的公钥为hi=g×fq(mod q) ，系统公钥。令S=，则计算追踪密钥为

6.2 签名生成算法

群成员j 要对消息B 进行签名，首先对消息B 使用hash 变换：H(B)，得到消息摘要m ∈[0,q)N。计算：

然后进行运算ϵ=-{ }x 和ϵ′=-{ }y 。

再计算：ej=ϵfj+ϵ′gj。

对于每个1 ≤i ≤N ，随机选取ri←Dr（其中Dr为小多项式的集合），计算Zi=ri×hi+ei(mod q)，然后通过判定语言Ls,γ和证据(ri,i)构造一个基于NIWI 的证明π ，输出加密的签名c=(γ,Z1,Z2,…,Zn,π)（其中γ 为构造NIWI证明时的参数）。

6.3 签名验证算法

本节中，NormBound 为验证签名是否合法的临界值，β 为平衡因子，其范围为0 ＜β ≤1。验证者首先设置mˉ=m||γ，然后验证π ，如果π 是正确的，且对于每个1 ≤i ≤N ，进行如下运算：

如果v ≤NormBound 则验证正确，输出1；否则输出0。

6.4 签名打开算法

7 安全性分析

7.1 正确性

本文方案签名过程基于NTRUSign算法，所以签名方案的正确性基于NTRUSign算法的正确性。在NTRUSign 算法中，假设有一个合法的签名，计算，则 必然有v′≤num 。在本文方案中，验证等式为v=，而对于一个合法的签名c=(γ,Z1,Z2,…,Zn,π),有Zi=ri×hi+ei(mod q),等式两边同时乘以f ：

根据NTRU格上的性质，小多项式g*r 的值是可忽略的，因此Zif=eif(mod q)。所以可以得到：v=v′≤num，即合法签名能通过验证算法的检验。

另外，由于本文方案方案利用NTRUSign算法得到的签名ej是距离消息摘要m 最近的NTRU 格点，而Zj=rj×hj+ej是对rj×hj轻微扰动后的NTRU格点。而群管理员通过追踪密钥TK=可以解密(Z1,Z2,…,Zn),此时求出(‖ Z1-h1r1‖,‖ Z2-h2r2‖,…,‖ Zn-hnrn‖)中最小值所对应的i，即为签名ej所对应的用户j。即通过关系式min‖ ‖Zi-hiri，群管理员可成功推导出c 为群成员j 所签。

综上，本文群签名方案满足正确性。

7.2 匿名性

本文方案通过证明一系列的游戏G0,G0′,G1′,G1[4]中，G0和G0′ 不可区分，G0′ 和G1′ 不可区分，G1′ 和G1不可区分来证明G0和G1不可区分，进而证明方案的匿名性。

定理1 如果DLWEm,q,α问题是困难的，那么游戏G0和G1具有计算不可区分性。

证明如果引理2、引理3、引理4可证，则定理1可证。

引理2 如果DLWEm,q,α问题是困难的，那么G0和G0′具有计算不可区分性。

证明首先定义D 和A，D 为一个概率多项式时间算法，试图攻破DLWEm,q,α难题，A 为模拟挑战算法，试图攻破G0和G0′ 的计算不可区分性。算法D 与算法A 进行交互，进行如下运算：首先，输入(f,y),D 首先随机选择i*←[N]，令fi*=f ，对于其他的i ≠i*，随机选择均匀分布的Fi，计算fq←Invert(f),A 可获得公钥和追踪密钥TK=,A 进行的哈希询问都可以得到正确的回应，结果A 输出i0,i ∈[N]和消息摘要m。此时结果若为i*≠i1，那么算法D 将随机输出一个比特后停止；结果若为i*=i1，算法D 将随机地产生数值ri←Dr，然后D 计算eio=ϵfio+ϵ′gio，并且满足条件v ≤num ，同理，对于其他的i ≠i1，Zi获得的方法和G0,G9′ 类似。如果i=i1，那么令Zii=y。设定Dy为y的均匀分布的情况，对A 而言，Dy和G0是统计接近的。在G0中，首先计算ei1=ϵfi1+ϵ′gi1，然后得到Zi1=ri1×hi1+ei1；在Dy′中，计算ei1=ϵfi1+ϵ′gi1，然后得到Zi1=ri1×hi1+ei1。由于D 停止的概率为1/N ，并且D 停止与A 获胜相互独立。如果A 以概率ε 区分出G0和G0′ ，则D 以概率ε/N 攻破了DLWEm,q,α难题，由此得出引理2。

引理3 如果游戏G0′ 和G1′ 基于的NIWI 证明系统满足证据不可区分性，则游戏G0′ 和G1′ 具有计算不可区分性。

证明证明游戏G0′ 和G1′ 具有计算不可区分性只需要证明在π 进行运算时所使用的证据的不同即可。方案中基于的是NIWI 证明系统，该系统具有证据不可区分性，其中G0′ 的证据为(ri0,i0) ，而G1′ 的证据为(ri1,i1)，因此可得到G0′和G1′是计算不可区分的。

引理4 如果DLWEm,q,α问题是困难的，那么游戏G1和G1′具有计算不可区分性。

证明证明G1和G1′ 计算不可区分性的过程与引理2证明过程类似，此处不再赘述。

由引理2、引理3 和引理4，可得出如果DLWEm,q,α问题是困难的，则游戏G0和游戏G1是计算不可区分的，即定理1得证。

7.3 可追踪性

可追踪性的直观定义是群管理员可以通过追踪密钥找到正确签名者的身份，意味着，所有合法产生的签名都是可追踪的，即使攻击者在拥有系统公钥，追踪密钥，但没有签名密钥的情况下，与任意群成员进行交互也无法伪造出一个合法的不能被追踪的签名。

本文所提方案的可追踪性证明包括两个方面：（1）证明合法产生的签名都是可追踪的；（2）证明攻击者伪造不出一个合法的不可追踪的签名。根据本文7.1节正确性可以得知，合法产生的签名都是可追踪的。下面重点证明（2）攻击者伪造不出一个合法的不可追踪的签名。定理2描述本文方案的可追踪性依赖于NTRUSign签名的不可伪造性，由定理2，假设攻击者伪造了一个合法的不可追踪的签名，意味着NTRUSign签名的不可伪造性被攻破，而NTRUSign 签名在Appr-CVP 的困难假设下是安全的，所以本文方案具有可追踪性。

定理2 假定存在一个概率多项式时间算法A（简称敌手A），执行询问后，能够以概率ε 攻破本文方案的可追踪性，那就会存在一个概率多项式时间算法F（简称敌手F）能以概率ε/N 攻破NTRUSign 签名的不可伪造性。

证明如果有敌手F，与另一个敌手A 进行交互试图攻击NTRUSign算法，首先，执行如下算法：

F 选定i*∈[N]，hi*=h，h 为F 所攻击NTRUSign方案的公钥，计算fq←Invert(f)，将公钥和追踪密钥TK=发送给A。对于A 的询问，F 进行如下回应：

（1）当询问私钥预言机时，假若i ≠i*，则将fp发送给A，当i=i*时，F 终止游戏。

（2）当询问签名预言机时，假若i ≠i*，F 利用fp计算合法签名然后发送给A；当i=i*时，F 会产生随机数值ri←Dr，然后再一次针对消息向自己的签名预言机进行询问，此时该预言机会计算出一个合法的签名ei*,然后发送给A。

（3）当询问其他预言机时，敌手F 会询问自身的随机预言机，然后将结果发送给敌手A。

设C 为通过私钥询问系统的i 的集合（当i*∈C时则A 终止）。经过交互询问后，A 输出一个消息摘要m 和 对 应 的 密 文c=(γ,Z1,Z2,…,Zn,π) 。如 果G.Verify(PK,m,c)=1,并且敌手A 的所有签名问询G.Sign(i,m)都能得到i ∈C 。此时由于F 有追踪密钥TK=，所以可得到群成员G.Open(PK,m,c)的信息。在j=i*时，F 利用恢复出，此时满足。然后输出伪造的签名；而当j ≠i*时，敌手F 停止游戏。

用ε 表示A 获胜的概率。 F 不终止游戏的概率为1/N ，A 在从未询问过G.Sign(i,m) 的基础上可以以ε/N 的概率输出满足条件G.Verify(PK,m,c)=1 ，G.Open(TK,m,c)=i*的签名(m,c)，对于上述签名(m,c)，其中c=(γ,Z1,Z2,…,Zn,π)。由于G.Open(TK,m,c)=i*，所以F 可以利用追踪密钥恢复出ei*，并且满足条件。由于G.Verify(PK,m,c)=1 ，那么可以得到v ≤NormBound ，即是对消息m‖ r ‖i*的合法签名，此时A 并未询问过G.Sign(i,m) ，也即F 从未对进行过签名询问就得到了合法签名。即敌手A 以概率ε 攻破了本文方案的可追踪性，那么在概率多项式时间内敌手F 也可以以概率ε/N 攻破NTRUSign签名的不可伪造性，定理2得证。

8 效率分析

本章选择七个优秀的格上群签名方案作为比较对象：Gordon等[8]在ASIACRYPT'10提出了第一个基于格的群签名方案（简称GKV2010 方案）；Laguillaumie 等[11]在ASIACRYPT'13 提出的签名长度大小为O(lb N)的格上群签名方案（简称LLLS2013方案）；Langlois等[15]在PKC'14提出的基于格的支持本地验证者撤销的群签名方案（简称LLNW2014方案）；Nguyen等[12]在PKC'15提出的签名长度大小为O(lb N)的格上群签名方案（简称NZZ2015方案）；Ling等[16]在PKC'15提出的基于环的更简单高效的格上群签名方案（简称LNW2015 方案）；Libert 等[17]在EUROCRYPT'16 提出的不需要陷门的格上群签名方案（简称LLNW2016方案）；Ling等[19]提出的格上全同态群签名方案（将其称为LLNX2017 方案）。表2 将本文方案与以上7 个方案在系统公钥长度、用户的签名密钥长度，签名长度以及是否需要陷门等方面进行比较。在表2中，λ 为安全参数，N 为群签名中用户的数量（其中N=2l），λ ≫l，O~ 为省略对数的计算复杂度。

表2 格上群签名方案的性能比较

在系统公钥长度方面，GKV2010 方案、LLLS2013方案、LLNW2014方案、NZZ2015方案、LLNW2016方案和LNWX2017 方案都是基于一般的格，其系统公钥尺寸较大，而本文方案使用的是NTRU 格，由于NTRU 格特殊的矩阵结构，使得本文方案中系统公钥的长度为O~(λl2)，由于λ ≫l，所以有O~(λ·l2)＜O~(λ2·l)，即本文方案的系统公钥长度均低于这六个方案，既节省了群签名算法中占用的存储空间又降低了计算复杂度和通信代价；LNW2015 方案是第一次基于环构造的格上群签名方案，系统公钥长度仍大于本文基于NTRU 格构造的群签名方案。在用户签名密钥长度方面，本文方案的用户签名密钥长度小于GKV2010 方案、LLLS2013 方案、LLNW2014 方案、NZZ2015 方案和LLNW2016 方案中用户签名密钥的长度，但是与LNW2015 方案和LNWX2017 方案中用户签名密钥长度相同，然而LNWX2017方案在签名的过程中，由于在对消息进行签名时，需要在时间点τ 检测群信息inf oτ是否一致，相比本文方案需要额外的时间、空间上的消耗。在签名长度方面，本文方案的签名长度比GKV2010 方案的签名长度小，原因在于虽然本文方案和GKV2010 方案都是基于NIWI 证明构造的格上群签名，但是本文方案基于的是NTRU格，产生签名过程只涉及到多项式环的乘法和小整数求模运算，使得本文方案构造的签名的长度小于GKV2010 方案中基于一般格构造的签名的长度；但本文签名长度比其他六个方案的签名长度大，原因在于本文方案在基于NIWI 证明构造群签名方案的过程中，需输出额外的证明信息π 来保证方案的匿名性，然而由引理1 可知，本文方案基于的NIWI 证明系统的长度为O(mnN lb q)bit，所以签名长度虽然偏大但还是在可接受的范围之内的。在陷门需求方面，本文方案不需要陷门，简化了整体的运算，使得密钥生成更加快速，且方案在选择参数时限制也会相对降低。

另外，表2 没给出计算速度的比较。在计算速度上，本文方案只涉及到多项式环上的乘法和小整数求模运算，使得计算效率提高，并且由于NTRU 格特殊的矩阵结构使得方案中系统公钥、签名密钥和追踪密钥是并行计算的，使得运算更加简单高效。

9 结束语

群签名具有匿名性、可追踪性等多种特点，在密码学领域发挥重要作用。而在量子计算机得到应用的前提下，传统基于数论难题构建的群签名方案都将在多项式时间内被破解，因而，研究基于格的群签名是具有重要意义的。传统的格上的群签名方案都存在计算复杂度高、通信代价大和系统公钥尺寸过大的弱点，研究格公钥密码尺寸更小的格上群签名成为该领域值得深入研究的问题。本文采用一种NTRU 格上高效生成参数的算法构建了一个基于NTRU格的群签名，该方案有如下优势：（1）缩短了系统公钥长度，节省了存储空间，使得空间消耗降低；（2）由于NTRU格的特殊结构，方案只涉及多项式环上的乘法和小整数求模运算，使方案中密钥生成更为高效，且易于并行计算，提升计算效率。

本文方案不足之处在于由于方案在基于NIWI证明构造签名的过程中，需要输出额外的证明信息来保证方案的匿名性，使得签名长度偏大。如何在保证安全性的同时使签名长度缩短，将是NTRU格上的群签名值得进一步研究的问题。