计算智能在电动车充电站规划的应用研究综述

王利利，张琳娟，尚雪宁，高德云

1.国网河南省电力公司经济技术研究院，郑州450000

2.北京交通大学 电子信息工程学院，北京100044

1 引言

近年来，在汽车销售市场中电动汽车的占比越来越高。2017年新能源汽车保有量达到122.78万辆，新能源汽车产销量居世界第一[1]。然而，对于电动汽车充电服务运营商来说，情况并不乐观。中国电动汽车百人会在2019 年4 月发布了《中国充电服务市场如何健康发展》研究报告。其中指出[2]，全国公共充电设施的平均小时利用率不足10%，这意味着充电运营商亟需通过优化电动汽车充换电站的布局来提升充电设施的利用率。

在充电桩建设规划布局的过程中，需要综合分析运营信息、交通信息、电网负荷等多种数据，公平合理地满足电动汽车用户、运营商、交通网管理部门、电网管理部门、环境保护等各方需求约束[3-4]。不同的充电桩部署方式可以对电动汽车用户满意度、运营商盈利情况、交通网拥堵情况和电网负荷情况造成不同的影响。因此如何寻找一个最优的充电桩部署方式来满足各方需求约束是一个典型的NP-Hard问题。

电动汽车充换电站的规划问题可以用大数据分析来解决。如图1 所示，车辆用户、路边基础设施和充电站可以通过无线接入网将数据上传。无线接入网内的边缘计算实体可以先对数据进行预处理，然后将数据上传给充电服务运营商的云计算集群。充电服务运营商通过综合分析用户的历史行为数据，可以有效地预测各地区的充电需求，从而优化电动汽车充换电站的部署方式，提升充电设施利用率。电动汽车充电服务大数据具有规模大、类型多、价值密度低和处理速度要求高等特点[5]。针对这样的特点，传统的统计分析方法无法很好地从数据中挖掘价值，这就需要通过计算智能方法来分析数据。文献[6]综合分析了现有的计算智能方法，将其分为人工神经网络、模糊系统、演化计算和群体智能并分别介绍了各自的特点与优势。由于演化计算和群体智能如遗传算法和粒子群优化算法比较适用于寻找全局最优解，对于解决充电站规划部署这种NP-Hard问题具有很高的应用价值。所以目前解决充电桩规划问题，主要应用遗传算法和粒子群算法来进行全局寻优求解。遗传算法具有很强的自适应性[7]，通过模仿基因变异和自然选择的过程，可以增加解的多样性，避免陷入局部搜索。粒子群算法则具有保留群体和个体的历史搜索信息的特点，收敛速度较快，容易实现[8]。针对充电桩规划问题，不仅需要合理的数学建模来描述问题，更需要对计算智能方法进行改进才能在保证解集多样性的前提下提升搜索的收敛速度。与此同时，人工神经网络所具有的在线学习能力可以进行实时充电需求预测从而更加合理地选择站址和划分服务范围，模糊系统对于模糊性现象的发掘可以用于缩减评价目标并发现数据中隐含的相关性关系。

图1 电动汽车充电大数据应用场景

2 遗传算法和粒子群优化算法概述

2.1 遗传算法原理概述

遗传算法最初由密歇根大学教授Holland 提出，是一种通过模仿种群进化过程寻找全局最优解的启发式算法，结合遗传算法基本流程[9-10]，应用于充电站规划的遗传算法流程如图2 所示。首先，输入初始站址坐标、充电需求热点和相关路网电网约束条件，通过对站址坐标编码构成初始种群。然后针对每个初始站址计算目标函数值，寻找出初步最优站址。随后按照适应度函数值对站址进行随机选择，通过交叉变异站址编码更新站址位置。再次进行适应度函数计算，比较更新最优站址，判断收敛条件。如果满足收敛条件则输出最优站址规划，否则再次进行交叉变异操作。

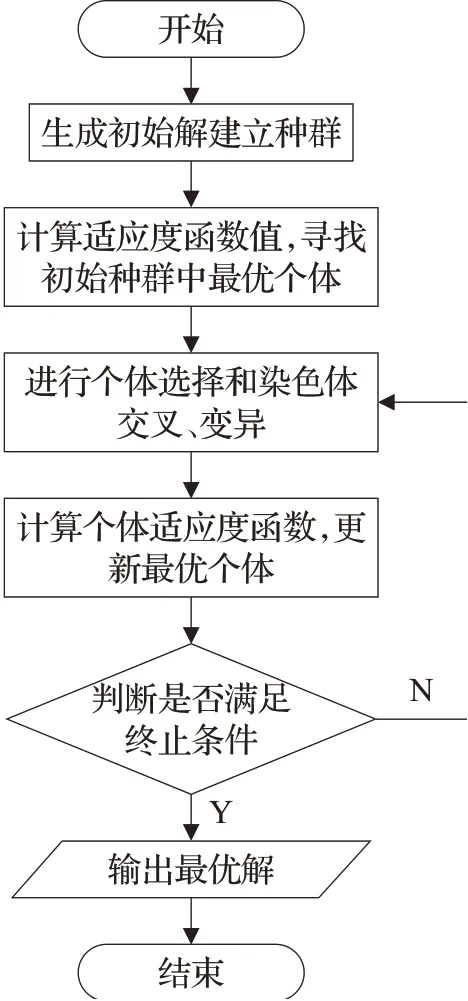
图2 遗传算法基本流程图

在应用遗传算法过程中，站址编码与染色体交叉变异的示例如图3 所示，初始种群为给定的多种站址方案，如果所选站址建站则该位置表示为1，否则为0，从而采用二进制编码站址方案。交叉操作则为两种站址方案之间某一位置的编码进行互换，而变异操作则可以通过指定某位取反。

图3 遗传算法原理示意图

在应用遗传算法求解具体问题时，染色体的编码规则、适应度函数的选取、遗传算子的设计以及算法参数的确定上需要针对具体问题分析，这也是应用遗传算法求解问题的难点所在[11-15]。只有通过合适的策略应用遗传算法，才能最大程度地保存种群的多样性，提升算法的准确性，使得算法能够更快地收敛至理想的结果。

2.2 粒子群优化算法原理概述

Kennedy 和Eberhart 在1995 年设计的粒子群优化算法是一种通过模拟鸟群觅食活动的群优化算法，主要用于解决寻找多目标连续函数的最优解问题[16-17]，结合粒子群优化算法基本流程[18]，应用于充电站规划的基本流程如图4所示。

图4 粒子群优化算法基本流程图

在求解时可以将充电站建设方案看作一个粒子，针对该方案内的所有充电站地理位置生成一组坐标。假设计划建设充电站数目为m，种群数量为n，则随机产生n 个粒子，每个粒子中包含m 组坐标用于确定站址的初始位置和速度。第二步计算各站址的适应度函数。第三步和第四步则分别选出个体和群体最优站址方案Pbid(t)和Pbgd(t)。第五步则根据式（1）至式（4）更新站址规划[18]，式（1）表示建址方案i 在d 维空间上的速度vid(t+1)由上一时刻粒子速度vid(t)与个体最优差值ΔPbid和群体最优差值ΔPbgd组成，式（2）表示个体最优差值ΔPbid通过个体最优位置Pbid(t)和粒子当前位置xid(t)的差值乘以随机数R1和个体惯性权重c1，式（3）表示群体最优差值Pbgd(t)与粒子当前位置xid(t)的差值乘以一个随机数R2和群惯性权重系数c2得出，粒子位置xid(t+1)则由粒子上一时刻位置与粒子速度的和得出。第六步判断是否已经得出收敛结果，得出则输出最优解，否则跳回第二步。在应用粒子群优化算法时，惯性权重系数的设置、收敛条件的限定、随机数的选取策略等会在很大程度上影响算法的性能[19-21]。而且该算法后期收敛速度较慢，容易陷入局部搜索导致算法早熟[22-26]。在应用时需要结合具体问题来弥补粒子群优化算法的缺陷。

3 电动汽车充电站规划问题研究

3.1 充电需求

在进行电动汽车充电桩规划问题建模时，首先要考虑的是正确预测充电需求热点。如图5所示，充电需求预测可以通过两种方式获取，一种是直接统计历史数据，另一种是间接预测出区域内的充电需求。直接式的充电需求分析是指通过原始数据直接得出充电需求的量化值。间接式充电需求预测则是指通过非直接相关数据挖掘其与充电需求的关系，比如通过社交网络、充电行为等非直接相关数据发现其与充电需求的关联规则，通过相似项分析的方法得出用户的充电需求。

图5 充电需求预测方式

区域内电动汽车保有量和交通流量的历史数据可以作为衡量区域内充电需求的主要指标[27-34]。

式（5）表示区域内充电负荷需求Breq与区域内电动汽车数量Ncar成正比关系，系数a 则为车辆平局充电需求负荷值。 Fave作为区域内年平均车辆流量可以作为充电站用户流量负载能力Fchar的最小值保证充电站符和交通流量需求。

区域内电动汽车数量Ncar和区域内年平均电动汽车流量Fave的数值可以通过利用蒙特卡洛方法求出[35-36]。蒙特卡洛方法可以通过历史数据的抽样实验得到变量的模拟分布[37]。通过统计分析电动汽车数量和流量的历史数据，可以得出充电需求沿时间的概率分布，从而得出充电需求的期望值。

除电动汽车保有量和交通流量以外，通过车主的充电行为模式和社交网络内的信息流也可以挖掘出充电需求的数量[38-40]。在大数据时代，任何信息都可以用于辅助决策。车主的充电行为可以充分反应用户的充电规律，充电运营商可以在服务过程中收集这类信息以辅助充电桩规划决策。除此之外，运营商也可以通过建立车主社交网络来进行信息的采集，一方面优化了用户的充电服务体验，另一方面也可以通过优化充电桩部署模式提升充电桩利用率。当然这种方式需要经过用户的允许，不能侵犯用户的隐私安全。

3.2 站址选择与服务范围划分

在确定需求热点之后，需要选择合适位置部署电动汽车充电站以及划分充电站的服务范围。Voronoi图可以将平面点集中的每个站点覆盖区域进行合理划分，从而达到区域内任意点与区域内站点之间的距离小于与区域外任意站点之间的距离[41]。采用变权的Voronoi图划分充电站点服务范围可以动态地反应所选站点的服务能力与服务半径[42]。最优充电站址点集的产生则需要通过演化计算和群体智能的方法寻找满足优化目标和约束条件的最优解集。

3.3 优化目标函数

电动汽车充电站规划问题的优化目标在于最小化电网管理者及充电运营商成本以及最小化用户充电成本[43-48]。

在进行充电桩部署决策时，充电运营商成本和电网管理者成本需要考虑多方因素进行合理的衡量。如式（7）所示，充电运营商成本和电网管理者成本C 由充电站建设成本Ccon、充电站运营维护成本Crun和配电网络损耗Cnet决定。式（8）表示充电站建设成本Ccon主要决定于土地成本Cland、变压器成本Cver、充电机成本Cmac以及折旧率ε。土地成本主要决定于用地面积与性质，变压器与充电机成本则主要决定于所用数量。折旧率ε 的表达式如式（9）所示，取决于折旧系数β 及使用年限y。充电站运营成本如式（10）所示，χ 为区域内每辆车每年的平均充电次数，δ 为每车每次充电为充电站带来的运行成本系数。配电网络损耗如式（11）所描述，由全局充电站数目Nsta和每个充电站的电网负荷系数φ决定。

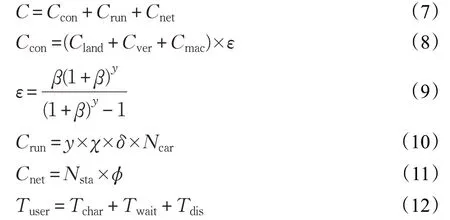
除了考虑充电运营商成本和电网管理者成本，充电用户充电成本也需要进行量化。用户充电成本Tuser的组成如式（12）所示，分别由用户充电时间成本Tchar、用户排队等待时间成本Twait和用户行驶至充电站的时间成本Tdis组成。用户充电时间成本由车辆类型、充电站类型决定，不同的车辆有着不同的充电时间，而快速充电站与慢速充电站的充电时间也各不相同。由于用户排队等待时间成本Twait可以通过M/M/s排队论模型求出其期望值[49-50]。用户行驶至充电站的时间成本Tdis则可以由需求点与供应点的平均距离进行衡量，从而得出用户驶往充电站的平均时间成本。

如图6 所示为待优化成本的主要构成。在进行优化时，考虑到充电站服务能力的提升虽然会降低充电者的充电时间成本与充电费用成本，但是与此同时充电运营商和电网管理者的成本也会增加。同时考虑到环保因素[51]，如何权衡多方利益，在最小化用户成本的前提下最大化运营商和电网管理者的收益将是充电桩规划问题的主要矛盾。

图6 优化目标示意图

3.4 约束条件

在进行目标优化函数求解时，还要考虑充电站容量、站址间隔等约束条件[52-58]。对于电力系统来说，一定区域内的充电负荷能力是有限的。所以在进行充电站规划时，区域内的充电负荷量应该不超过区域内供电负荷上限。与此同时，为满足充电需求，充电站容量也应大于充电用户的基本需求量。式（13）反映了充电负荷的约束条件。式中Pmin表示区域内充电基本需求量，Pmax表示区域内供电负荷上限，Psta(i)表示第i 个站址的充电负荷量。

为保证充电站的分布符合城市用地规划并满足用户需求，站间距离应保持在一定范围内。如式（14）所示，Dmin表示站间最小距离以保证充电桩部署方案不符合实际用地限制，Dmax表示站间最大距离以保证满足用户需求，Dsta(i)则为第i 个充电站距离最近的充电站的距离。

受制于充电站建设规划成本，充电站建设总数量应当小于投资金额所能建设的最大充电站数量。如式（15）所示，投资金额Mp与平均建站成本Me的比值作为建站数量Nsta的上限值约束总充电站数量。

路网交通条件也会作为充电站规划的约束条件。充电站的建设会引来大量的交通流量，为防止交通拥堵，充电站交通流量也应有所约束。如式（16）所示L(i)表示充电站点i 附近的道路集合。式（17）表示充电站点i 的最大交通流量Fmax(i)由每条道路的最大交通流量Fli组成。式（18）表示站点i 所产生的交通流量F(i)应当小于路网限制的最大值。

如图7 所示为充电站优化问题的主要约束条件。为模型建立约束条件，可以保证算法求解数学模型时不会出现脱离现实的解，提升算法的收敛性能与速度。而另一方面，为快速准确地求解电动汽车充电桩规划问题，针对该问题改进演化计算和群体智能方法是不可或缺的。

图7 优化目标示意图

4 充电桩规划问题中的计算智能应用研究

4.1 遗传算法应用研究

采用遗传算法求解充电桩规划问题，需要对站址进行编码，根据目标函数构造遗传算法的适应度函数，并根据算法流程求解。如表1 所示为遗传算法在电动汽车充电站规划问题中的应用研究。文献[59]根据区域交通流量守恒定律将区域车辆密度设为常数，应用传统的遗传算法进行了分析，采用排序算法选择最优个体，简单实用、适应性强。文献[60]基于地理信息排除不适合建站的位置，缩小数据集。在求解时采用算术交叉更新染色体，引入定位分配算子，结合交叉分配定位算法，具有较好的全局搜索和局部搜索能力，同时将充电者的时间成本予以考虑，实现了社会综合效益的最大化。文献[61]综合考虑电网约束、交通流量约束和运营成本约束，对约束条件进行了详细的分析，使用量子遗传算法求解，采取了更合适的编码方式，具有收敛速度快的优势，然而由于缺少充电运营数据，算法参数设计仍不完善。文献[62]则对充电桩进行快充桩和慢充桩的区分，建立多等级的电动汽车充电设施选址模型，同样采用遗传算法求解。文献[63]则主要针对电动出租车的充电行为进行规划，采用Voronoi 图的方法划分充电站的服务范围，利用排队论的方法确定充电站的容量，使用量子遗传算法自适应调整策略，根据迭代次数调整旋转角，具有更好的遍历性。文献[64]通过分层遗传算法求解问题，采用双层的编码策略并引入了检查算子和禁忌表，从而更好地满足约束条件并且提升了算法性能。

使用遗传算法可以很好地解决充电站规划问题，通过合理的染色体编码以及自适应的交叉变异策略，可以在保证解集多样性的前提下提升算法的收敛速度。同时，在应用遗传算法解决电动汽车充电站规划问题时，可以针对问题的特点对算法进行相应改进。比如修改离散编码方式为连续编码方式以提升算法搜索能力、采用量子编码进行交叉变异丰富解集多样性、增加新的算法流程剔除不合适的解、融合其他算法提升算法效率等等。如何针对电动汽车充电站规划问题改进遗传算法，仍有很大的研究空间。

4.2 粒子群算法应用研究

除了遗传算法意外，粒子群优化算法也很适合用于电动汽车充电站的规划。由于粒子群优化算法是以粒子坐标为搜索对象，所以非常适合充电桩的选址规划问题。

表1 遗传算法应用研究

如表2 所示为粒子群优化算法在解决电动汽车充电站规划问题中的应用总结。文献[65]以居民负荷模拟车辆数量，采用层次分析法给出候选站址权重系数。综合分析站址与变电站距离、充电站安装费用和运行费用以及实时电价，采用粒子群算法进行模型求解。文献[27]使用Voronoi 图和改进粒子群优化算法联合求解规划问题，优化了惯性权重和学习因子，提高了搜索的速度。同时在每次迭代过程中更新Voronoi 图，可以直接根据车辆密度信息进行站址规划，使得站址选择能够更好地契合应用需求。文献[28]采用量子理论中的叠加态特性和概率表达特性，利用量子旋转门进行状态更新，利用量子非门引入编译操作，增强了算法全局搜索的能力，提升了迭代速度。文献[66]采用差分进化混合粒子群算法，同时进行粒子群算法和差分进化算法，比较二者平均适应度，在二者的最优个体之间进行交叉变异和最优位置替换。在保证多样性的同时具有很好的收敛性。文献[42]采用改进的概率映射函数来解决混合离散粒子群算法中后期收敛速度慢、局部搜索能力弱的问题。采用变权Voronoi 图的方法，为每个站点赋予可变的权重，更加合理地划分了覆盖范围。文献[67]针对粒子群得出解集的非劣性使用VIKOR方法对解进行排序得出最优解。文献[68]采用混合的遗传算法和粒子群优化算法，通过染色体交叉和变异操作增加解集多样性，在保证搜索速度的同时增加了解集的多样性。

粒子群算法具有个体间可以相互交流信息的特点，在收敛速度上具有一定的优势，但是容易陷入局部搜索、丧失粒子群的多样性，而且局部搜索能力偏弱。对于粒子群算法在充电桩规划问题上的应用研究，主要集中于将粒子群算法与其他算法融合，提升粒子群算法局部搜索能力和保持粒子群多样性的同时仍然具备较好的收敛能力。

4.3 其他算法应用研究

解决全局寻优问题的多目标优化算法，除了遗传算法和粒子群优化算法，还有教学优化算法、禁忌搜索算法、人工免疫算法等。这些算法都可以解决充电桩规划的问题。文献[69]采用MOTLBO（Multi-Objective Teaching-Learning Based Optimization，多目标教学优化算法）算法对充电规划问题进行求解，通过综合分析需求，将优化目标定为最小化充电需求与充电位置的总里程数、最小化充电桩建设代价、满足其他约束条件等多个目标。经评估该算法在反世代距离评价指标（Inverted Generational Distance，IGD）和最优解集的广泛性方面具有很好的表现。文献[70]以最大化覆盖交通流量、最大限度减少充电时间、最大化充电桩利用率、最大化运营商收入为优化目标，利用旅行链的方法确定充电需求，采用人工免疫算法求解问题。文献[71]设计了一种多等级的充电站选址模型，并用改进的禁忌算法进行求解。文献[72]通过MOEA/D（Multiobjective Evolutionary Algorithm based on Decomposition，基于分解的多目标进化算法）算法求解充电桩规划问题，通过分解目标优化问题，对子问题同时进行优化，可以达到降低计算复杂度的目的。

这些算法都在一定程度上为解决充电桩规划问题提供了借鉴，多目标教学优化算法可以有效提升算法效率、人工免疫算法可以保证解集的多样性而禁忌算法则可以根据之前的搜索结果优化搜索过程，可以说每种算法都有自己的优势。

4.4 人工神经网络和模糊系统的应用研究

与传统的针对历史数据进行充电需求预测的方式不同的是，人工神经网络可以通过在线学习的方式预测充电需求。文献[73-74]设计了一个用于学习路况信息和交通流量拥塞等级的机器学习框架，并且提出了一种预测用户驾驶环境的机器学习算法，可以有效地预测路网信息和用户驾驶倾向。文献[75]提出了基于小波神经网络算法的智能用电网交互系统负荷预测方法，将小波算法与人工神经网络结合，加快收敛速度的同时赋予其去噪能力。文献[76]提出了一种基于深度学习和人工神经网络的容量规划预测方法，通过分析路网信息、电网信息等多方面要素，训练充电环境与需求的映射模型。文献[77]则针对电动公交车进行了能量估算的研究，通过采用电池使用数据训练人工神经网络模型，从而估计车辆的电池利用情况。可以发现，人工神经网络在充电需求预测方面有着很好的应用前景。无论是直接式的充电需求预测和间接式的充电需求预测，都是一种反应式方式，通过对历史数据的分析从而得出区域充电需求热点。然而，人工神经网络所具有的在线学习特点则可以实现一种预知式的充电需求预测。如路网信息、电网负荷、用户电池使用情况、用户驾驶行为等信息可以实时上传给云数据中心，使得充电需求可以更加准确地预测出来。

表2 粒子群优化算法应用研究

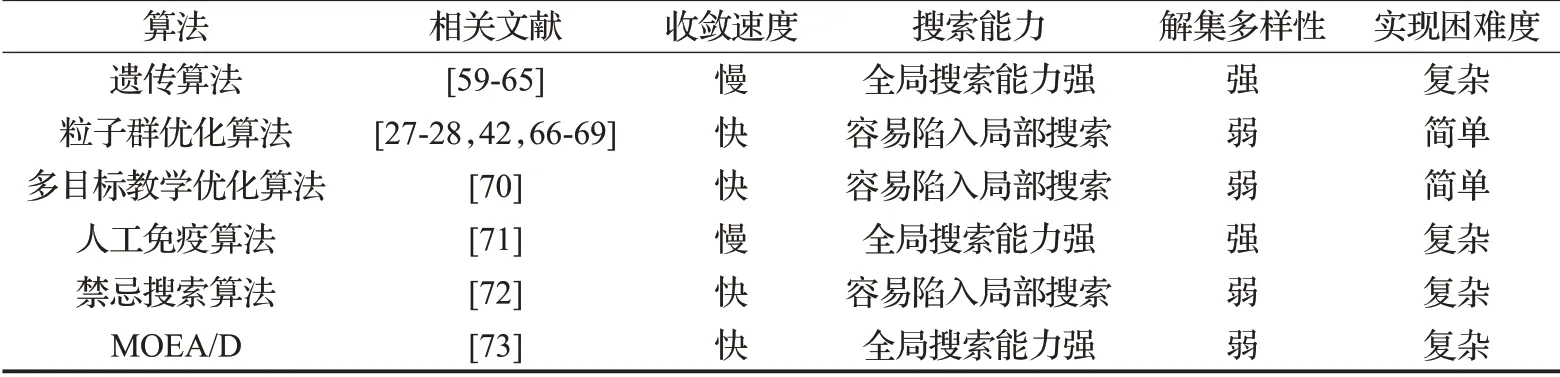
表3 各算法优缺点对比

表4 各计算智能方法应用对比

模糊系统在充电桩规划问题中的应用则分为两类。其中一类[78-80]将模糊系统应用于充电站规划方案的评价中，在评价已有充电站规划方案时，由于评价指标过多导致无法对充电站进行综合性的评价。采用模糊系统的方法可以对评价指标进行约简，通过构造多种评价指标与单种综合指标的模糊映射关系，从而评判充电站规划方案的优劣。而另一类[81-83]则是应用模糊系统将多目标充电站规划问题转化为单目标规划问题，与上述应用不同的是，模糊系统是通过与演化计算与群体智能的结合在求解最优解的过程中起作用。通过构造模糊隶属度函数，将多个目标函数模糊化，然后根据优先级或满意度建立单目标函数，从而解决多目标优化各个目标函数之间的冲突问题。以上两种应用都是将具体的问题模糊化，然而如何将模糊的问题具体化却是模糊系统最鲜明的特点。比如对于充电用户的充电服务反馈来说，往往是模糊的“好”与“坏”，其中影响用户体验的因素并不能显式地体现出来。通过模糊系统的聚类分析方法可以发现影响用户体验的相关因素，发现未知的相关性关系或得出已知的相关性关系之间的重要程度，从而为充电规划做出更加清晰的指导。

4.5 充电桩规划优化算法讨论

衡量演化计算和群体智能算法的标准，主要集中于收敛速度、解集多样性、避免陷入局部搜索的能力、实现困难度等方面[84]。如表3 所示，遗传算法和人工免疫算法具有很好的避免陷入局部搜索的能力，然而在收敛速度上有所欠缺，实现也较为复杂。粒子群算法、教学优化算法虽然实现困难度较低、收敛速度也较快，但是却容易陷入局部搜索，丧失解集多样性。禁忌搜索算法具有很好的收敛速度和解集多样性，但是实现过于复杂。综合比较各种算法，可以说各有优劣也各有特色。如果使用单一算法解决问题，在解决问题时不能达到最好的效果。所以，不同的算法混合应用可以很好地利用各个方法的优势，取长补短，解决充电桩规划问题。

除此之外，针对人工神经网络、模糊系统、演化计算和群体智能在充电站规划问题中的应用特点来说，不同的计算智能方法可以用于解决不同的问题。如表4 所示，针对演化计算和群体智能方法解决复杂优化问题的优越性以及二者互补的特点，可以采用混合算法对充电规划问题进行求解。对于人工神经网络来说，针对电动汽车充电用户具有很强的移动性，充电需求热点也会根据交通情况而变化，采用人工神经网络方法可以动态实时地分析用户的充电需求，从而为站址选择提供更加精确的信息。对于模糊系统而言，其强大的模糊聚类分析能力不仅可以简化已有充电站的服务能力评价以及化简多目标优化问题，同时也可以通过相关性分析发现影响充电站规划的隐性因素，从而让充电站的规划部署更好地为用户服务、为运营商盈利。

5 结束语

本文通过总结演化计算在电动汽车充换电规划中的应用，为提升充电桩利用率提供了研究的方向。通过综合电动汽车充换电规划的数学建模方法，给出了优化的目标函数和约束条件，对充电需求预测方法进行了探讨。分析对比了遗传算法、粒子群优化算法、教学优化算法、人工免疫算法和禁忌搜索算法在充电桩规划问题中的应用情况。对演化计算和群体智能针对充电桩规划问题所做出的改进进行了分析。对比分析了人工神经网络、模糊系统、演化计算和群体智能在充电站规划问题中的应用特点，展望了各自的应用前景。