FastICA算法的收敛性与一致性分析

马倩茹，冶继民

西安电子科技大学 数学与统计学院，西安710126

1 引言

主成分分析（Principal Component Analysis，PCA）[1]是一种被广泛使用的统计方法，但它是基于二阶统计量展开的，只能估计模型的某一方面。本文主要讨论另一种统计方法，独立成分分析（Independent Component Analysis，ICA）[2-3]。ICA基于高阶统计量，可以更加全面地分析和处理相关实际问题。最初提出ICA 是为了解决鸡尾酒会问题，后来随着大量学者对ICA 的研究，它也被应用到很多其他领域，比如：语音信号、生物医学信号、图像信号等。其中，主要被用于处理盲信号分离问题。ICA是假设未知源信号相互独立，从源信号的线性混合（观测信号）中分离出未知源信号的方法，整个混合过程只有观测信号是已知的（混合过程和源信号均未知）。自从Hyvärinen 和Oja 提出ICA 这个概念以来，无数的学者对该统计方法展开研究，包括：算法的变形、性质、应用等。截止目前为止，已经出现了很多种ICA 方法，例如：极小化互信息法、信息极大化法（Informax）、快速ICA法（FastICA）等。本文主要研究的是FastICA[4-5]算法，实验证明，它在收敛速度方面优于大多数ICA算法。

FastICA 算法分为两种：（1）one-unit（或deflation）FastICA，一次只能分离一个源信号；（2）对称FastICA，可以同时分离多个所需的源信号，等价于几个one-unit FastICA并行。针对这两个版本的FastICA算法，很多学者做出了相应的研究。文献[6]中将源信号的先验知识作为参考信号，附加到FastICA算法中，减少估计所得的源信号与真实源信号之间的误差，并将其应用于处理生物医学信号问题。其实文献[6]的改进是可行的，因为对现实生活中的信号并不都是一无可知的，所以可以把已知的相关信息作为参考信号加入到信号估计中。文献[7-8]将FastICA 算法扩展到复数领域，用以处理复值信号。文献[9]中的FastICA 算法允许使用不同的非线性提取不同的独立成分，减少了因非线性的选取对估计效率和鲁棒性的影响（此处的非线性并非数学意义上的非线性，在第2 章有详细的定义）。文献[10]和文献[11]使用HuberM-估计和改进的M-估计作为非线性函数，以提高算法的鲁棒性。近年来，除以上的研究以外，对FastICA算法收敛性、渐进性、一致性等统计及数学性质的相关研究更是不少。文献[12]表明了归一化引起的额外旋转不会影响算法的收敛速度，而文献[13]则是使用主纤维束的概念，证明了算法局部二阶收敛到正确的分离。文献[14]证明算法可以达到Cramér-Rao 下界。由此可见，FastICA研究相当广泛，本文将研究扩展到样本领域。

本文主要给出FastICA 算法的收敛性与一致性分析。第2章和第3章是基础，主要介绍了ICA算法、全集FastICA 算法以及基于样本的FastICA 算法的数学模型。第4章证明了FastICA算法的相关收敛性质。首先证明了全集FastICA 算法的收敛性质，主要包括定理1所述的不动点定理，以及对比函数局部极大值和全集FastICA算法迭代函数不动点的关系。紧接着通过构造狄拉克函数，并且利用依概率收敛定理和大数定律，给出了基于样本的FastICA算法收敛性条件和相关收敛性质，证明了基于样本的fastICA 算法给出分离向量的估计是无偏的。在第5 章，证明了FastICA 算法给出的估计具有一致性。无偏性、一致性是评判估计方法的两个重要标准，无偏性保证了FastICA 算法给出的分离向量的估计无系统偏差，一致性保证了在获得较多样本的条件下，能够得到更准确的估计值。

2012年，学者Reyhani N使用经验过程的相关理论和P-Donsker，以及P-Glivenko-Cantelli的性质证明FastICA的一致性[15]。本文通过比较直观的统计方式证明FastICA的一致性，并且通过仿真模拟证实随着样本数目增加，FastICA估计所得源信号更加接近真实的源信号。

2 ICA数学模型

经典的ICA数学模型如下：

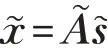
（1）si(i=1,2,…,m)期望为0，方差为1，即Cov(s)=I。

（2）A 是非奇异的正交方阵，即假设m=n。

ICA的基本思路是寻找分离矩阵使得y=Wx 尽可能相互独立。W 称为分离矩阵，W 的行向量w 称为分离向量。因为A=(a1,a2,…,an)是正交的，所以行向量w 是分离向量当且仅当存在i ∈{1,2,…,n}使得w=ai或w=-ai。

文献[2-3]提出通过极大化wTx 的负熵来求解w，负熵J(·)∝E(G(·)-G(v))2，其中，G(·):R →R 被称为非线性，通常假设为二阶连续可导的非二次偶函数，且v服从标准正态分布N(0,1)。所以：

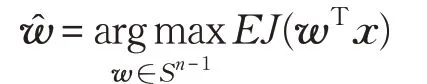
其中，Sn-1:={w ∈Rn|‖ ‖w =1}，E{·}表示对观测信号x取数学期望，实际中用样本均值替代。上述优化问题进一步等价于极大化或极小化对比函数M(wTx)=E[G(wTx)]，本文以极大化为例，即：

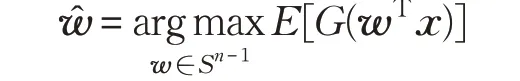
文献[2]中提出3 种可选的非线性，峭度：x4/4 ，gauss:-exp(-x2/2)，tanh:lg cosh(x)。

3 FastICA算法

3.1 全集FastICA算法

通过使用拉格朗日乘子法求解上述优化问题，得到全集FastICA算法如下所示：

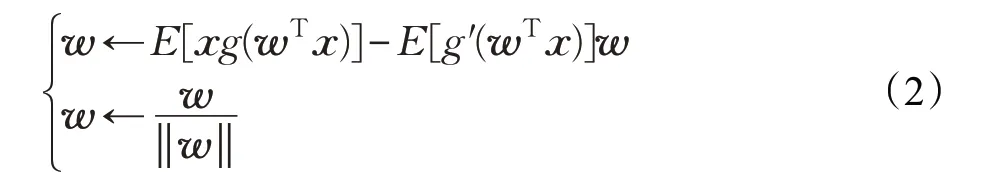
迭代式（2）中的g(·)和g′(·)分别表示非线性G(·)的一阶导数和二阶导数。文献[2]中提供了上述FastICA算法的详细推导过程。推导采用的是牛顿迭代的方式求解拉格朗日方程。整个推导过程中采取了两次逼近。2017年，S.Basiri等学者[16]根据源信号的独立性，给出了新的推导方式，没有用到两次逼近，同样得到上述结果。本文中将式（2）称为全集FastICA。

3.2 基于样本的FastICA算法

式（1）是经典的ICA 模型，但是在实际中可以得到的是如下的样本形式：

文献[2]中已经提出了模型（3）所示的样本ICA 模型，本文主要研究其相关性质。与模型（1）类似，对模型（3）也做如下的说明和假设：

（1）每次样本实现是独立同分布的。

（3）A 是未知的非奇异正交方阵。

（4）观测信号x(t)同样需要白化。白化过程中的期望和协方差阵分别用样本均值和样本协差阵估计，即：

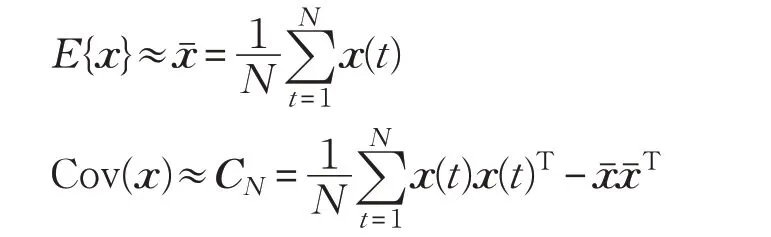
假设模型（3）的x(t)已经被白化过，不难验证，白化后的x(t)样本均值为零向量，样本协差阵为单位阵，称模型（3）为基于样本的ICA 模型。同样的，用样本均值代替式（2）中的数学期望，得到的算法称为基于样本的FastICA算法。

4 收敛性分析

4.1 全集FastICA收敛性分析

近年来，很多学者研究了FastICA算法的收敛性，比如文献[2，12-13]。为了下文对基于样本的FastICA算法收敛性进行探讨，首先以更加简洁的方式证明全集FastICA 算法收敛性能的相关内容。将全集FastICA 算法式（2）分解为两个函数，并定义一个新函数：

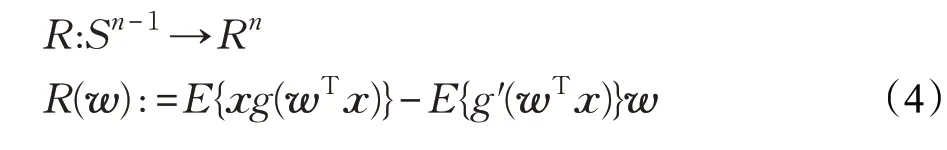
可以看出R(·)和T(·)是根据全集FastICA 算法式（2）定义的，而U(·)则是根据文献[2]中全集FastICA算法局部收敛性条件定义的，收敛条件叙述如下。

引理1（收敛条件）假定输入数据符合ICA模型，数据z=VAs 是白化过的随机向量（其中V 是白化矩阵），而G(·)是一个足够光滑的偶函数。那么在约束下，混合矩阵VA 的逆矩阵中某行使得E{G(wTz)}取相应的局部极大值（或极小值，是极大值或极小值由下面公式中对应的“＞”或“＜”确定），当且仅当相应行对应的独立成分si满足：

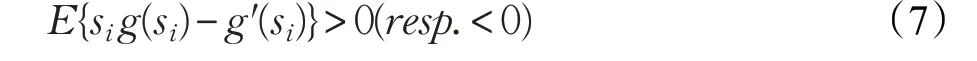
式中，g(·)是函数G(·)的导数，而g′(·)是g(·)的导数。

由表1可知，棚内温度要小于棚外温度，绿棚温度高于黑棚温度；湿度以棚外最高，并且黑棚的湿度高于绿棚；光照度以棚外最高，绿棚高于黑棚，并且棚内直射光线明显减少，而漫射光线增多。

不等式（7）与U(·)的定义一致。引理1 表明，任何非二次函数G(·)只要满足E{sig(si)-g′(si)}≠0，就可以将概率密度空间分为两个半空间，而两个半空间分别对应式（7）取正负的两种取值。分布落在其中一个半空间的独立成分，可以通过极大化对比函数E{G(wTz)}来估计，而落在另一个空间中的分布，则可以通过极小化相同的函数进行估计。当U(w)≠0 时，全集FastICA算法可以收敛到混合矩阵的第i 个列向量ai。不失一般性，本文以极大化空间为例，即假设U(ai)＞0 ，此时ai是E{G(wTz)}的极大值。基于上面的假设，定理1成立。

定理1（不动点定理）混合矩阵A 属于正交矩阵集合O(n):={A ∈Rn×n|ATA=I}，ai是混合矩阵A 的第i列，U(ai)＞0，则ai是函数T(·)的不动点。

证明设矩阵A 有如下形式：A=(a1,a2,…,an)，则：，此处。将ai带入式（4），得：

上述推导中应用了si的相互独立性和E[si]=0 。且

由于定理1是基于ai可以实现正确分离，即达到对比函数M(wTx)的极大值成立的，所以，如下的定理2成立。

定理2 如果x*是M(wTx)=E{G(wTx)}的局部极大值，则它是函数T(·)的一个不动点。

4.2 基于样本的FastICA收敛性分析

为了分析基于样本FastICA 算法的收敛性，以及描述和证明FastICA 估计的一致性，参照文献[17]中M-估计和Z-估计的定义和一致性定理，引入对比函数M(wTx)的一个近似。首先构建一个观测样本x(t)的概率密度函数（8）：

其中，δ(x)被称为狄拉克δ 函数，是一个广义函数，该函数在除了零以外的点取值都等于0，而在整个定义域上积分等于1，即：。显然，δ(x)满足概率密度函数的充要条件：（1）非负可积；（2）正则性，在整个实轴上积分等于1。且函数δ(x)具有如下的性质：

因此，对于式（8）的pN取函数期望，可以得到：

本文中EN(·)表示对于概率密度函数式（8）取数学期望。所以，可以重写式（4）～（6）为如下样本形式：

并且，对比函数M(w)也可以定义为如下样本形式：

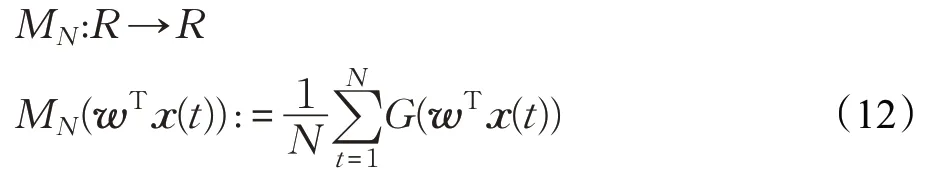
此处的MN即为M(wTx)的近似。为了方便下文的证明，在此假设E∞，且：

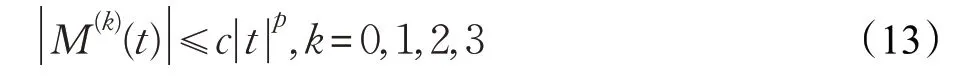
式中c 和p 是正常数。文献[18]中采取了类似的假设，并且解释了该假设的可行性。对于第2章的3个经典非线性函数，峭度：x4/4,gauss:-exp(-x2/2),tanh:lg cosh(x),至少存在p=4 的情形使得不等式（13）成立。可以证明，4.1 节的引理1、定理1、定理2 推广到基于样本的FastICA 算法依然成立。分析可知，只需要证明UN一致收敛到U 即可。首先引用文献[19]的依概率一致收敛定理。

引理2 假设x(t),t=1,2,…,N 是一个n 维变量分布的样本，θ 是紧集Θ ∈Rn上的随机向量。 h(x,θ) 是Rn×Θ 上的Borel 可测函数，使得∀x,h(x,θ)是连续函数，且E＜∞，则：

引理2其实是加强版的强大数定律，该引理的具体相关内容可以在参考文献[18]中找到。根据引理2很容易证得式（9）～（12）均依概率一致收敛到式（4）～（6）和M(wTx)。

定理3 假设w ∈Sn-1，且G(·)是连续函数，以下依概率一致收敛成立：

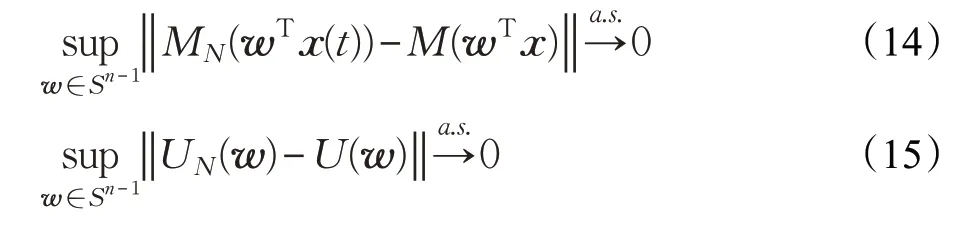
证明只需证明式（14）、（15）满足引理2 的条件即可。显然，Sn-1是紧集。由于G(·)的连续性，所以第二个条件也满足。现在只需证明期望有界即可。

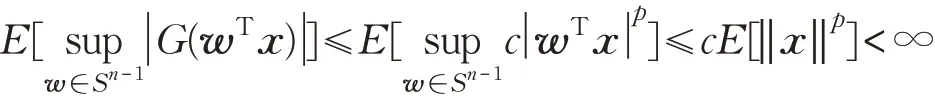
当然也可以将函数G 看成算子，因为连续算子与有界算子等价，所以

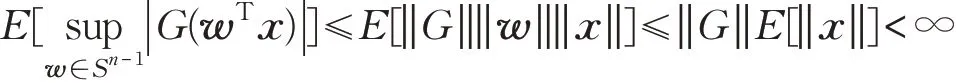
因此，式（14）成立。同理

所以式（15）成立。

由于引理1、定理1 以及定理2 都是基于条件：U(w)＞0，根据定理3中式（15），显然它们可以扩展到基于样本的FastICA算法。所以基于样本的FastICA算法也是收敛的。在下一章一致性分析中，会用到式（14）的结论。引理1的扩展如定理4所示。

定理4 假设输入数据符合模型（3），数据x(t)已经白化过。在约束‖ ‖w =1 下，混合矩阵A 的某列ai可以使取得相应的局部极大值（或极小值）：当且仅当对应的独立成分si(t)满足：UN(ai)＞0(resp.＜0)。

定理1和定理2可类似推广。

5 FastICA的一致性

文献[15]讨论了FastICA 估计的一致性，但是是从经验过程的相关理论和P-Donsker，以及P-Glivenko-Cantelli 的性质讨论的。本文从概率论角度重新证明FastICA 算法得到估计的一致性。文献[17]中有经验过程的具体介绍。一致估计是指当样本数量充分大时，抽样样本指标充分接近总体指标。换句话说，一致估计等价于估计依概率收敛到真实值。

如文献[15]所述，FastICA 算法得到的估计是一种M-估计，或Z-估计。文献[17]第5章详细介绍了M-估计和Z-估计，极大似然估计是最常见的M-估计。从文献[2]关于FastICA 算法过程，可以看到，分离向量的估计w^是通过类牛顿法求解方程：Ψ(w):=E[xg(wTx)]=0，所以该估计可以看做Z-估计。引用文献[17]定理5.9来证明FastICA估计的一致性，具体内容如引理3所述。

引理3 假设Ψn(θ)是随机向量函数，Ψ(θ)是固定向量函数，且∀ε ＞0，下列两式成立：则：任意估计序列θ^n依概率收敛到θ0且Ψn(θ^n)=op(1)。

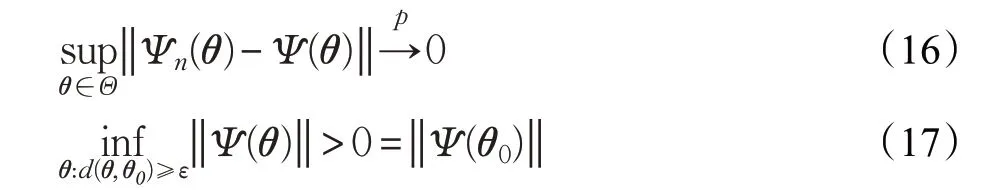
结合引理3与文献[17]可知，随机序列Ψn(θ)的零点依概率收敛到固定序列Ψ(θ)的零点。引理3 中符号op(1)表示依概率收敛，具体内容和运算可以参考文献[17]的2.2节。本文取：

定理5（FastICA 的一致性）假设ai可以分离得到正确的源信号si，且E[g′(si)]≠0、，则由Ψn(w):=En[x(t)g(wTx(t))]产生的FastICA估计是一致的，p

证明根据引理3，证明一致性，只需证明式（16）、（17）成立即可。根据引理2，式（16）成立只需证明：E＜∞。同定理3证明：

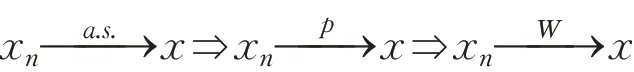
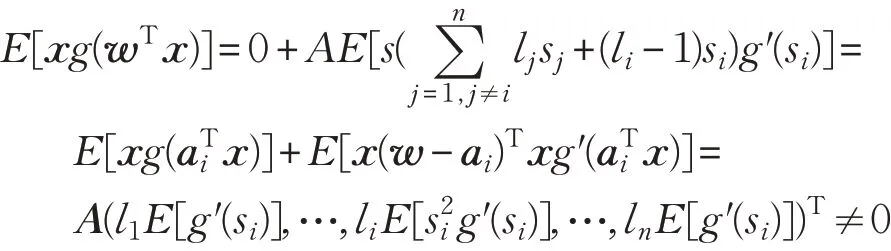
本文假设函数G(·)为偶函数，则E[g′(si)]≠0 、0。因此，上式成立。FastICA 估计的一致性得证。

6 计算机仿真

此部分仿真主要分为两方面，一方面验证FastICA算法具有良好的分离效果，另一方面验证FastICA 估计的一致性。

为了验证分离效果，采取如图1（a）所示的3张512×512的灰度图像作为源信号，使用matlab2017b随机产生混合矩阵，进而得到图1（b）混合信号。采用经典FastICA算法（2）分离源信号，得到图1（c）。式（2）中出现的数学期望用样本均值mean代替，非线性选取tanh:lg cosh(x)。由于ICA算法估计出的图像信号的幅值存在不确定性，会出现图像偏白或偏黑的情况。为了给出逼真的图像效果，将ICA 给出的图像估计的灰度值进行放缩变换，使变换后灰度值最大的像素点的灰度值为255，灰度值最小的像素点对应的灰度值为0。避免了图像偏白或偏黑的情况。从图1可以看出，源信号和分离信号除去顺序不一致，基本可以分辨出相互之间的对应关系。由此可见，FastICA的良好分离性能。

图1 图像分离效果

一致性指随着样本数目增加，分离信号与源信号之间的差距逐渐变小。为了验证FastICA 的一致性，选取4种波形信号：正弦波信号、方波信号、锯齿信号、随机噪声作为实验对象，并且不同的样本数目为200 和2 000。实验结果如图2和图3所示。图2和图3分别为N=200与N=2 000 的情形，两个实验对应的源信号选取均为上述4 种波形信号，源信号相同，只有样本数目不同。明显可以看出，图3的分离信号更加接近源信号。而图2的分离信号，尤其是锯齿形信号，很明显与源信号相差较远，源信号是光滑的，但分离信号则不是。由此可见，当样本数目增加时，分离矩阵可以更好地被估计，分离得到的源信号与真实的源信号更加接近。由此，验证了FastICA估计的一致性。

为了更进一步说明一致性，引入FastICA 评估的性能指标（Performance Index，PI）。文献[20]中有关于指标PI 的详细介绍及计算公式。等距样本数目区间为[0,500]、[500,1 000]、[1 000,1 500]、[1 500,2 000]、[2 000,2 500]、[2 500,3 000]、[3 000,3 500]、[3 500,4 000]、[4 000,4 500]、[4 500,5 000]，对于每一个样本区间，运行100次，随机产生100 个样本数，并取整，计算每次的PI 值，并且求得平均的PI 值，运行结果如表1 所示。根据文献[20]，PI值达到10-2，一般可以达到较好的分离效果，且PI 值越小，分离效果越好。观察表1 中的PI 值，随着样本数目的增加，PI 值明显递减。因此，一致性又一次得到证明。

大量的实验结果表明，当样本数目大于等于独立分量数目的10 倍以上时，一般均可以达到较好的分离结果，而自适应类的ICA算法达到收敛时需要的样本数目远远大于独立分量数目的10倍。例如，在本实验中，选取样本数目为40时，PI值已经可以达到0.001 663 94，此时，FastICA算法具有良好的分离效果。

图2 样本N=200 分离效果

图3 样本N=2 000 分离效果

7 结束语

本文将FastICA 算法写成样本形式，并且分别分析了全集FastICA算法和基于样本的FastICA算法的收敛性。证明了FastICA算法对比函数局部极大值和迭代函数不动点之间的关系，并且通过引理2 的大数定律，将其扩展到基于样本的FastICA算法。本文的另一个重要内容是运用概率论的方法证明FastICA估计的一致性。

表1 不同样本数目PI均值对比