基于环形芯光纤的超低差分模式增益涡旋光纤放大器

古 皓， 汤 敏， 曹 敏， 芈月安， 陶 洪，李雪健， 任文华， 简 伟， 任国斌*

(1. 北京交通大学 全光网络与现代通信网教育部重点实验室， 北京 100044；2. 北京交通大学 光波技术研究所， 北京 100044)

1 引 言

轨道角动量(Orbital angular momentum, OAM)模式复用是空分复用的一种实现方式。具有不同拓扑电荷数的OAM模式彼此正交，并且理论上其拓扑电荷数是无穷的[1]。因此，将OAM模式用于光纤通信系统来提高通信容量是目前的研究热点,已有大量研究报道[2-4]。光纤放大器是光纤通信系统中的重要器件，实现OAM模式放大的光纤放大器称为涡旋光纤放大器[5]。为了实现光纤通信系统中OAM模式复用长距离传输，研究涡旋光纤放大器对OAM模式的增益特性具有重要意义。

差分模式增益(Differential mode gain,DMG)是涡旋光纤放大器的一个重要性能指标，用于描述OAM模式的增益特性，其定义为：在涡旋光纤放大器中，同一波长下的不同OAM模式增益的最大差值[6-7]。当利用OAM模式承载信号并进行传输与放大时，通过设计光纤中铒离子掺杂分布等方式减小差分模式增益，有利于降低光纤通信系统的误码率[8]。涡旋光纤放大器一般基于涡旋光纤结构，近年来，已有涡旋光纤结构能够较好地支持OAM模式传输，如空芯光纤结构[9]、环形芯光纤结构[10]、光子晶体光纤结构[11]等。2015年，Kang等基于空芯高折射率环的光纤结构，在高折射率环的部分区域掺杂铒离子，该光纤放大器支持12个OAM模式，C波段所有模式增益大于20 dB，DMG小于0.25 dB[9]。2015年，Ma等基于环形芯光纤结构，在高折射率芯层的内边缘与外边缘进行双环铒离子掺杂，该光纤放大器支持18个OAM模式，C波段所有模式增益大于20 dB，DMG小于0.28 dB[10]。2018年，Han等在光子晶体光纤中进行双环铒离子掺杂，该光纤放大器支持14个OAM模式，C波段所有模式增益大于22 dB，DMG小于0.1 dB，并且噪声系数小于4 dB[11]。总的来看，近年来提出的涡旋光纤放大器可支持的OAM模式数量小于20，DMG最小为0.1 dB。因此，在提高支持OAM模式的数量和减小DMG方面，涡旋光纤放大器的性能有进一步提升的空间。

本文提出了一种可以支持22个OAM模式(|l|=1～6)的高折射率环形芯光纤。在纤芯的部分区域进行铒离子掺杂作为涡旋光纤放大器的有源光纤。通过数值方法研究了掺铒离子分布、掺铒光纤长度、掺铒浓度与抽运功率对涡旋光纤放大器中OAM模式增益特性的影响。进一步优化光纤放大器的各个参数，提升了光纤放大器的性能。

2 基本原理

2.1 OAM模式

OAM模式可以由传播常数相同的本征矢量模式的偶模和相差π/2的奇模线性组合而成，并且OAM模式在传输时不会受到模间色散影响[12]。光纤中的OAM模式表示为OAM±l,m，其中l(l=1，2，3,…)为拓扑电荷数，代表OAM模式的阶数，m为径向模式强度分布对应的径向阶数。OAM模式可用下列公式表示[13-14]：

(1)

(2)

设计OAM模式传输光纤，需要遵循以下原则[13]：(1)设计出的OAM光纤需要满足OAM模式的强度分布，即环形分布；(2)为了使OAM模式能够在光纤中稳定传输，需要使同阶矢量模式有效分离(同阶矢量模式有效折射率差大于10-4)；(3)优化传输层厚度以避免在OAM模式传输过程中激发径向高阶模，影响OAM模式解复用。

2.2 掺铒光纤结构

为了能够使矢量模式简并分离，光纤结构需要满足高折射率梯度和高模场梯度[13]。本文设计了环形芯光纤结构，并对结构参数进行优化，图1为掺铒光纤结构的示意图。低折射率芯层与包层均可采用熔融石英玻璃制作，其折射率分别为n1=ncl=1.444，在石英玻璃中掺杂二氧化锗可以制作高折射率环形芯层[15]，其折射率为n2=1.514；低折射率芯层的半径为r1=8 μm，高折射率环形芯层的厚度为d=2 μm，包层半径为62.5 μm。x1与x2分别为环形铒离子掺杂区域的起始半径和终止半径，环形区域内各位置的铒离子掺杂浓度相同。

图1 掺铒光纤结构示意图

图2 光纤中的矢量模式。(a)信号模式归一化强度；(b)模式有效折射率随波长的变化；(c)模式间有效折射率差随波长的变化。

Fig.2 Vector mode in optical fibers. (a)Normalized intensity of signal modes. (b)Effective refractive index as a function of wavelength for different modes. (c)Effective refractive index difference as a function of wavelength between different modes.

该光纤结构支持14种矢量模式的传输，图2(a)为信号波长1 550 nm时的矢量模式归一化强度分布，可以看出，模式的能量很好地被束缚在高折射率环内。工艺上可以通过在x1～x2的环形区域进行铒离子掺杂，使各模式增益均衡[16-17]。图2(b)、(c)分别为各矢量模式的有效折射率和同阶OAM模式组的矢量模式间有效折射率差随波长的变化关系。由图2(b)可以看出，光纤中可以存在6个OAM模式组，即HE21与TE01、HE31与EH11、HE41与EH21、HE51与EH31、HE61与EH41、HE71与EH51，分别对应OAM模式阶数|l|=1，2，3，4，5，6。由于模场的增大，所有矢量模式的有效折射率随波长的增大而减小。由图2(c)可以看出，光纤中同阶OAM模式组(|l|=1，2，3，4，5，6)的矢量模式间有效折射率差Δneff在C波段(1 530～1 565 nm)均大于1×10-4，可以实现所有矢量模式的简并分离。因此，除了TE01、TM01、HE11模式，其余11个矢量模式的奇偶模可以各自分别组成波前相位旋转方向相反的两个OAM模式在光纤中稳定传输，即设计的光纤结构总共可以支持22个OAM模式(|l|=1～6)在光纤中稳定传输。

2.3 放大器理论模型

图3为光纤放大器的示意图。本文考虑了正向抽运、正向信号与正、反向噪声(Amplified spontaneous emission,ASE)的传输。在该模型中，做出如下假设：(1)将放大模型简化为二能级系统；(2)忽略离子浓度猝灭的影响；(3)不考虑模式耦合的影响。

图3 光纤放大器

对于噪声的处理，采用全光谱分析法将ASE光谱划分为M个不同的通道，每个通道的中心波长为λASEm，m=1,2,…,M，每个通道宽度记为Δλ，取值与信号光带宽相等，则ASE的功率传输方程形式与信号相同[18-19]。

描述光纤放大器中信号与噪声功率传输与放大的速率方程组，如公式(3)～(7)所示[18-19]:

N=N1(z)+N2(z),

(3)

(4)

(5)

(6)

为了具体分析不同信号模式间增益差值的变化情况，引入DMG(ΔG)的数学定义如下：

(8)

其中，Pin, i和Pout, i(Pin, j和Pout, j)分别是在信号波长为λs的情况下，第i(j)个信号模式的输入和输出功率。

对上述速率方程组进行求解时，采用多层法将光纤横截面分成离散环状单元[20]，在每一单元中分别计算粒子数密度和填充因子，再对环状单元累计求和得到信号和ASE的功率，从而可以进一步分析信号模式的增益特性。

3 数值仿真与分析

求解速率方程时，设定抽运模式为基模HE11。掺铒光纤放大器数值模拟参数见表1，其中，σas与σes为信号波长1 550 nm时的值。

表1 掺铒光纤放大器的初始参数

通过2.2节对掺铒光纤结构特性的分析以及2.3节对DMG的定义，可得：(1)当信号光模式阶数0<|l|≤6时，所有矢量模式简并分离，可以形成相应的OAM模式进行传输，此时的DMG取决于传输OAM模式的数量，当传输|l|=1～6的OAM模式时，DMG最大；(2)当信号光模式阶数|l|>6时，同阶矢量模的有效折射率小于10-4，无法形成稳定的OAM模式在光纤中传输，此时的DMG计算不考虑|l|>6的模式。因此，下文将讨论在信号波长为1 550 nm的情况下，|l|=1～6的所有OAM模式增益特性。如图4所示为DMG随x1和x2变化的二维分布，研究发现，图形是关于右斜对角线对称的，并且在右斜对角线附近可以取得DMG最小值。当掺杂区域的起始半径x1<8 μm时，随着终止半径x2的增大，DMG逐渐减小至最小值后基本保持不变；当x1>8 μm时，随着终止半径x2的增大，DMG逐渐减小至最小值，后增大至稳定不变。当掺杂区域的终止半径x2<10 μm时，随着起始半径x1的增大，DMG逐渐减小至最小值，后增大至稳定不变；当掺杂区域的终止半径x2>10 μm时，随着起始半径x1的增大，DMG先保持不变，后逐渐增大。因此，可以在右斜对角线附近寻找使DMG最小的掺杂起始半径x1与终止半径x2。研究分析可得，当x1=6 μm、x2=11 μm时，DMG最小为0.012 dB。后续研究将选取掺杂铒离子区域为6～11 μm，使得光纤放大器中OAM模式的DMG最小。

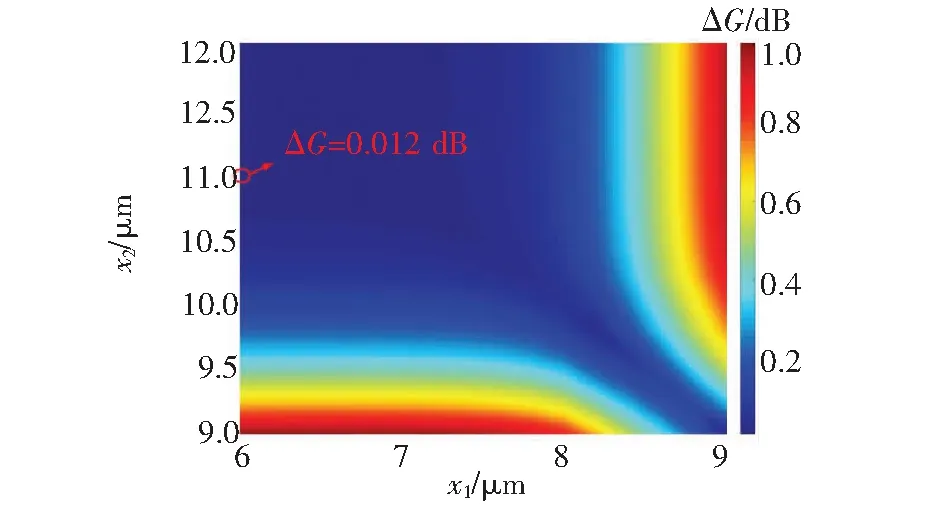
图4 DMG随x1和x2变化的二维分布

Fig.4 Two-dimensional distribution of DMG as a function ofx1andx2

当光纤放大器的参数为表1中的数值模拟参数时，图5(a)中用实线表示了其模式增益随光纤长度的变化。在光纤长度在0～5 m范围内，随着掺铒光纤长度的增大，模式增益迅速增大，当掺铒光纤的长度继续增大时，模式增益将基本保持不变，达到饱和状态，增益值约20 dB。出现这种趋势的原因是，随着光纤长度的增加，处于亚稳态的铒离子受信号光激励，迅速向基态跃迁，辐射出大量与入射光子完全相同的光子，使信号光能量迅速增大，信号模式增益迅速增大；随着亚稳态能级上的铒离子逐渐减少，受激辐射出的光子数减少，信号模式增益逐渐趋于平缓；当基态与亚稳态能级粒子数达到稳态平衡后，信号模式增益保持不变。图5(a)中的插图表示了光纤长度5 m附近的模式增益情况，可以看出，模式间增益差值小于0.012 dB，并且模式增益平缓，趋于饱和。

图5(b)表示了正、反向噪声功率随光纤长度的变化。可以看出，在z=0位置的ASE功率要明显高于z=L处的功率，并且其斜率的绝对值更大，这是由于在增益介质的前端有更高的粒子数反转密度[21]，随着光纤长度的增加，信号模式迅速获得增益，反向噪声功率因信号功率的快速增大而受到抑制，因此会迅速减小至趋于0；随着光纤长度的增加，信号模式增益在5 m处基本达到饱和，继续增加光纤长度，信号功率对噪声功率的抑制作用减弱[22]，因此5 m后的正向噪声功率逐渐增大。

结合上文对正、反向噪声功率的研究分析，在图5(a)中用虚线描述了信噪比(Signal-to-noise ratio,SNR)随掺铒光纤长度的变化。可以看出，在输入端，由于信号还未获得足够的增益，反向的噪声功率大于信号功率，因此信噪比为负值。随着掺铒光纤长度的增加，Rsn(信噪比)呈现先增大后下降的趋势。出现这种趋势的原因是，在信号与噪声的传输过程中，当模式增益达到饱和后，粒子数的抽运不充分，导致ASE噪声功率呈指数型增大。从图中可以看出在5 m处，信噪比达到最大值约27 dB，随后会逐渐下降。

图5 信号模式增益、噪声功率和信噪比随光纤长度的变化。(a)信号模式增益与信噪比随光纤长度的变化；(b)正、反向噪声功率随光纤长度的变化。

Fig.5 Gain of signal modes, power of ASE and SNR as a function of fiber length. (a)Gain of signal modes and signal-to-noise ratio as a function of fiber length.(b)Positive and reverse power of ASE as a function of fiber length.

由图5可得，当光纤放大器的参数为表1中的数值模拟参数时，存在使模式增益基本饱和且输出信噪比最大时的光纤长度，即5 m，后续研究将选取光纤长度为5 m，以减小噪声对信号模式增益的影响。

图6为信号模式增益、DMG与SNR随铒离子掺杂浓度的变化。图6(a)中，随着掺杂浓度的提高，信号模式增益与DMG均会逐渐增大后趋于平坦，这主要是因为提高铒离子掺杂浓度，会发生更多的粒子数反转；但由于抽运功率一定，提供给粒子数反转的能量一定，粒子数反转会到达一个极限，之后再增大掺杂浓度，也不会有更多的铒离子从基态跃迁到亚稳态。图6(b)中，增加铒离子掺杂浓度，粒子自发辐射产生噪声的几率也会相应增大，而信噪比曲线首先有一个增大的趋势，是因为铒离子浓度在一定范围内的增大，信号模式在与噪声的竞争中占优[22]，对信号模式的放大效率大于ASE。当信号模式增益趋于饱和，随着掺杂浓度继续增大，ASE的功率仍在增大，从而导致信噪比达到一个最大值后下降。

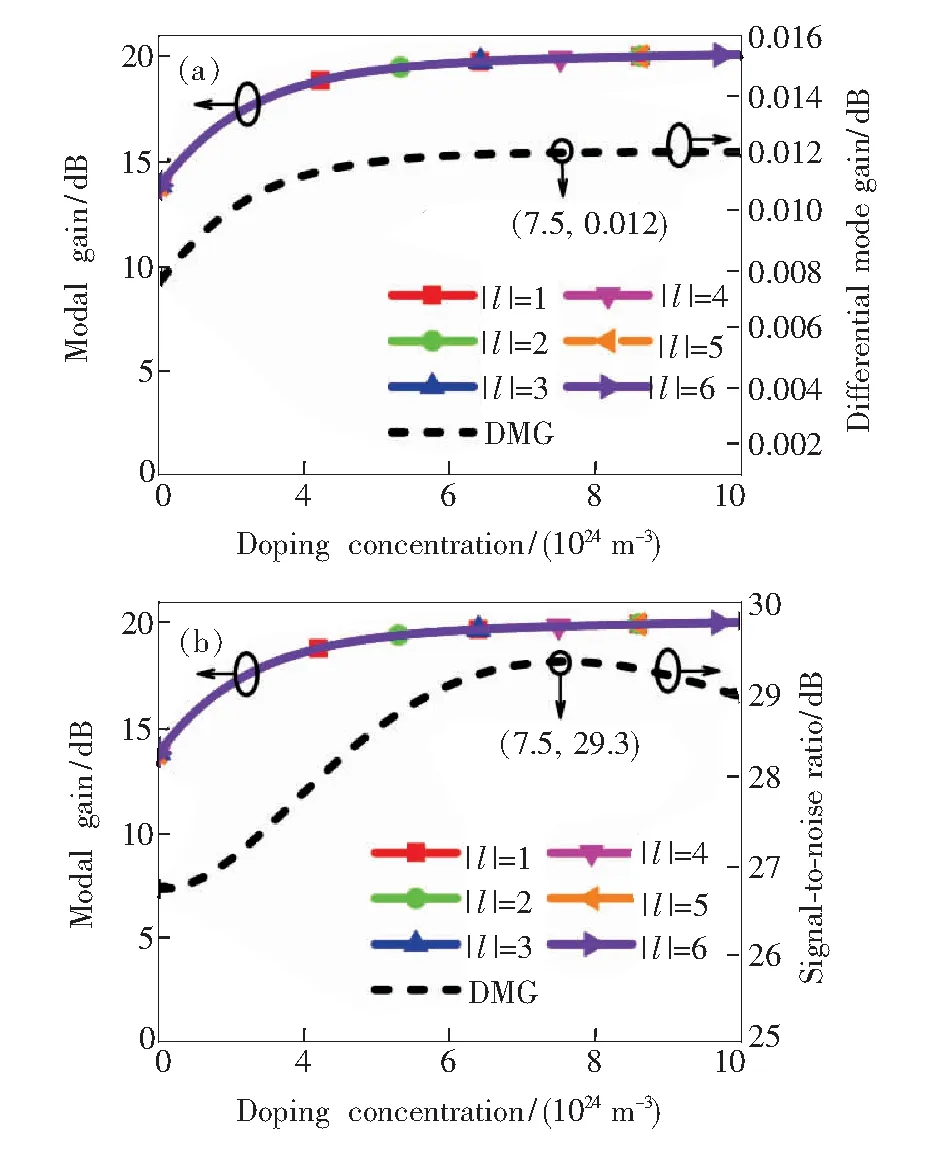
图6 信号模式增益、DMG和SNR随掺铒浓度的变化。(a)信号模式增益与DMG随掺铒浓度的变化；(b)信号模式增益与SNR随掺铒浓度的变化。

Fig.6 Gain of signal modes, DMG and SNR as a function of erbium-doped concentration.(a)Gain of signal modes and DMG as a function of erbium-doped concentration. (b)Gain of signal modes and SNR as a function of erbium-doped concentration.

由图6可得，当掺铒浓度为7.5×1024m-3时，信号模式增益约为20 dB，SNR为29.3 dB，DMG为0.012 dB。考虑到模式增益基本饱和，噪声对信号的影响最小，以及DMG较小，后续研究将选取掺铒浓度为7.5×1024m-3。

一般而言，抽运功率的大小会影响粒子数反转的程度，进而影响信号模式的增益、DMG与SNR。图7为信号模式增益、DMG与SNR随抽运功率的变化。图7(a)中，随着抽运功率的增大，信号增益逐渐增大至趋于饱和，这主要是因为当掺铒浓度一定、有足够的抽运能量使几乎所有铒离子进行粒子数反转时，再继续增加抽运功率，也不会有更多的铒离子从基态跃迁到亚稳态；而随着抽运功率的增大，DMG也逐渐增大，在总体上仍可保持较小的值，在抽运功率为1 W时，DMG约0.016 dB。图7(b)表明，SNR的变化在抽运功率小于0.5 W时与信号模式增益曲线相似，随着抽运功率的增大，SNR逐渐增大趋于平坦；当继续增大抽运功率至大于0.5 W时，SNR出现下降的趋势，这是由于当信号模式增益饱和时，噪声功率依然随着抽运功率的增大而增大。

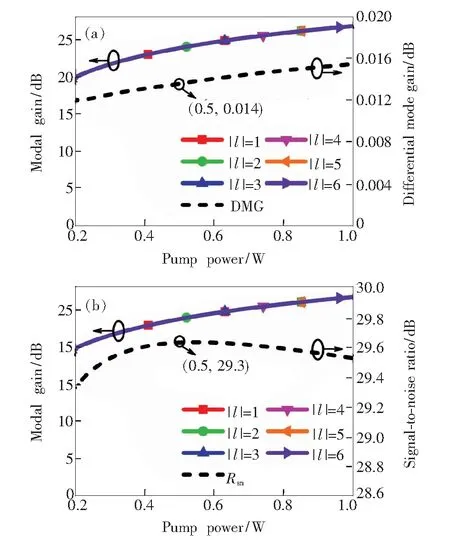
图7 信号模式增益、DMG和SNR随抽运功率的变化。(a)信号模式增益与DMG随抽运功率的变化; (b)信号模式增益与SNR随抽运功率的变化。

Fig.7 Gain of signal modes, DMG and SNR as a function of pump power. (a)Gain of signal modes and DMG as a function of pump power. (b)Gain of signal modes and SNR as a function of pump power.

由图7可得，当抽运功率为0.5 W时，信号模式增益约为23 dB，SNR为29.63 dB，DMG为0.014 dB。考虑到模式增益基本饱和，噪声对信号的影响最小，以及DMG较小，后续研究将选取抽运功率为0.5 W。

图8 C波段信号模式增益、DMG和SNR随波长的变化。(a)C波段信号模式增益与DMG随波长的变化；(b)C波段信号模式增益与SNR随波长的变化。

Fig.8 Gain of signal modes, DMG and SNR as a function of wavelength at C band. (a)Gain of signal modes and DMG as a function of wavelength at C band. (b)Gain of signal modes and SNR as a function of wavelength at C band.

根据以上研究结果，将光纤长度设为5 m，掺铒浓度设为7.5×1024m-3，抽运光功率设为0.5 W。图8(a)为信号增益与DMG在C波段的变化曲线，可以看到，信号模式增益随波长的增大呈现逐渐降低的趋势，其最大值约23.93 dB，最小值约23.77 dB，相差小于0.16 dB；而DMG随信号波长的增大而增大，其最小值约0.013 dB，在C波段整体小于0.015 dB。图8(b)中，由SNR随波长的变化曲线可以看出，随着波长的增大，SNR先减小后增大，到达一个最大值后再次减小，其最大值约30.3 dB，最小值约27.4 dB。在C波段，SNR整体大于27.4 dB，有效地减小了噪声对信号模式增益的影响。因此，该光纤放大器具有良好的性能。

4 结 论

本文提出了一种环形芯光纤，该光纤结构可以支持22个OAM模式(|l|=1～6)的稳定传输。研究发现，光纤放大器的最佳性能受光纤长度、铒离子掺杂分布与浓度、抽运功率的影响。在信号波长为1 550 nm的情况下，综合考虑了模式增益、DMG与SNR的指标要求，选择了掺铒区域为6～11 μm，可以使DMG最小为0.012 dB；进一步选择了光纤长度为5 m、掺铒浓度为7.5×1024m-3以及抽运功率为0.5 W，可以使SNR最大分别为27.02 ，29.30，29.63 dB。最后，该光纤放大器可以实现C波段(1 530～1 565 nm)所有OAM模式增益大于23 dB，SNR大于27 dB，DMG小于0.015 dB。所设计的光纤放大器支持22个OAM模式稳定传输，可用于提高光纤通信系统传输容量；其差分模式增益小于0.015 dB，并且受噪声的影响较小，可以避免信号光失真，降低误码率。