非相干光点扩散函数的重建及其在同步辐射成像系统中的应用
2020-01-17夏慧娟吴衍青孙元鹤邰仁忠
夏慧娟 吴衍青 张 磊 孙元鹤 邰仁忠
1(中国科学院上海应用物理研究所 上海 201800)
2(中国科学院上海高等研究院 上海 201210)
3(中国科学院大学 北京 100049)
X射线成像技术在医疗、安检、工业探伤、无损检测等领域中具有举足轻重的地位。由于X射线能量较高,所以实际应用中往往利用X射线的荧光效应将X射线转化为可见光进行间接成像。尤其对于高能X射线同步辐射光源,间接成像探测器比直接探测寿命长,接收能量范围高,而且容易实现。但是由于在转换过程中受到各种因素,尤其是高折射率的影响,X射线间接成像质量有待提高。
在成像技术中,经常通过图像的反卷积算法来消除成像系统的各种不理想因素,如离焦、运动模糊、光学介质畸变等不利影响。这些反卷积算法在X射线成像技术中也有不少应用。这些算法分为非盲去卷积算法和盲去卷积算法两大类[1-2]。前者更适合精确恢复图像。目前常用的非盲去卷积算法有近邻法、逆滤波法、维纳滤波法、线性最小平方法等线性算法[3-4];Jansson-Van Citter法、非线性最小平方法等约束迭代法,最大似然法、最大后验概率法等统计迭代方法;稀疏自适应网络、完全卷积学习网络等新方法[5-7]。这些算法计算量普遍较大,且都需要事先估计成像系统的点扩散函数(Point Spread Function,PSF)才能得到复原图像;盲去卷积算法一般也需要预估PSF。PSF是衡量光学系统成像性能的数学工具,是恢复图像过程中消除成像系统各种不利因素影响的关键。PSF估计准确与否直接影响了图像恢复的效果。其估计方法大致分为实验测量估计和计算构建估计两类。
在X射线闪烁体成像系统的PSF估计中常用的实验方法有传统边缘法、斜边法、微孔测量法、微聚焦测量法等[8-9]。前两种方法用于估计成像系统的噪声图像边缘角度存在不准确性。在微孔测量法中,微孔孔径过大会导致PSF估计误差大;过小的微孔只能在薄片上加工,其厚度不足以阻挡X射线的高能辐射,同样导致较大误差;微聚焦测量法要求将光斑聚焦到一个像素点以内,一般都在1 μm以内。对测量设备要求高,操作难度大;而且聚焦到微米级大小,光斑的能量会很大,探测器非常容易饱和,总之实现难度较大。一般来说,实测的PSF噪声不易控制,这对图像反卷积不利。在计算构建估计方法中,首先构建某种数学模型,然后根据各种形式的反馈信息修正该模型的参数,最终得到一个复原误差可以接受的PSF模型。如基于小波分析的高斯PSF估计[10],基于值平面上梯度矢量分布的PSF估计[11]等。总体来说,计算构建类方法不会有噪声等因素干扰,但目前该类方法普遍比较复杂,并且只适用于比较简单成像系统的PSF获取,如运动模糊图像和散焦模糊图像的PSF估计,对于复杂PSF的估计能力较弱,方法缺乏普适性。
本文采用微孔-反卷积测量法测量PSF,使用直径为20 μm的微孔进行测量,并用抗噪声效果较好的Lucy-Richardson算法进行反卷积[12],得到信噪比理想的PSF。由于该算法不能满足PSF中央区域的高精度要求,我们利用非相干PSF光信息分布的非定域性重建了PSF中央区域[13]。本文以一种X射线新型闪烁体成像系统为例,利用重建后的PSF获得了较为理想的图像反卷积效果,验证了该方法的有效性。
1 理论分析
1.1 非相干光PSF测量中的问题
通过有限离散化处理之后,PSF可以看成一个几何点(δ函数)在其像平面上许多有限尺寸像点的叠加。

由式(1)可知,已知微孔的物分布和像分布后,通过反卷积得到我们需要的PSF[14]。因此,测量PSF实验方案是采用大小合适的微孔,成像之后做反卷积,得到PSF。这应该是一种比较可行的方法。
常用的反卷积函数包括维纳滤波器(Wiener)复原,正则化(Regularized)滤波器复原和Lucy-Richardson方法复原。在知道清晰图像和噪声频率特性的情况下,维纳滤波器复原被看作是一种有效的图像复原技术。正则化滤波器也是在知道噪声信息的情况下有效的反卷积方法。但是,我们实验中图像频率和噪声信息都是未知的,而Lucy-Richardson滤波器方法假设噪声服从泊松分布,基于贝叶斯理论使产生图像的似然性达到最大值,不需要已知噪声信息和图像频率特征,保留了原始数据的计数性和非负性,抗噪声性能比较好,每次迭代的结果都是非负的,并且对PSF中的小错误具有很强的鲁棒性。因此我们选择Lucy-Richardson方法复原[15]。
Lucy-Richardson方法虽然具有很多优点,但是它也存在一定的误差,特别是区域小,边缘锐利的情况下,会存在很大的误差[16]。在实验中测量的PSF,由于-1级衍射光受非线性效应影响小,使-1级信息失真小,另外-1级区域面积大,强度远小于0级信息的强度,用Lucy-Richardson方法做恢复,误差小。Lucy-Richardson方法广泛应用,大部分应用情况下,该方法都可以满足精度要求,而我们研究中,0级包含图像细节信息,因此我们对0级的精度要求更高。
1.2 CTF-PSF和OTF-PSF的关系及信息冗余
由衍射光学的知识可知,非相干成像的光学传递函数(Optical Transfer Function,OTF)等于同等透镜条件下相干衍射受限系统的相干传递函数(Coherent Transfer Function,CTF)的自相关归一化函数[17]。PSF的傅里叶变换就是光学系统的传递函数。CTF-PSF是指在相干光照明下成像系统的PSF;OTF-PSF是指在非相干光照明下成像系统对应的PSF。因此:

式中:h(x0,y0;xi,yi)是由菲涅尔衍射公式计算而来的 CTF。其中:d0为物距,di为像距;(x0,y0)为物平面上一点坐标,(xi,yi)为像平面上一点坐标;dU′(x0,y0;x,y)是光波经过孔径函数 P(x,y),焦距为透镜后的单位脉冲响应的复振幅。将式(3)带入式(2)中并化简可以得到式(4)。
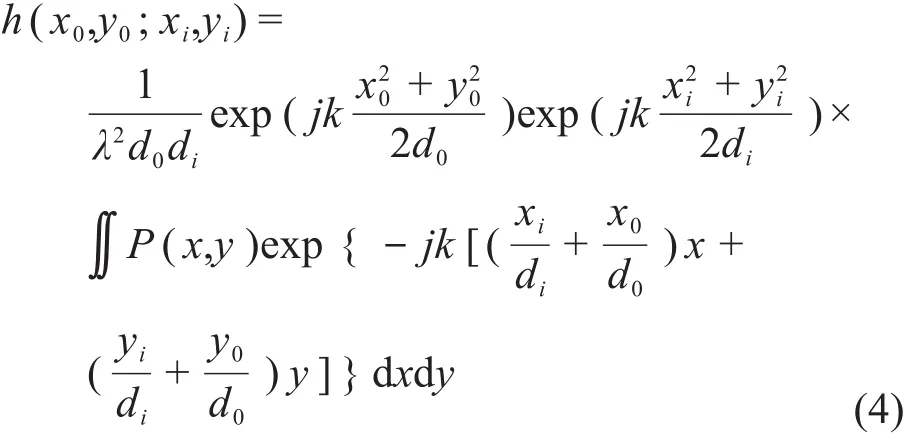
式中:积分号前面的相位因子不影响最终的衍射强度分布,在讨论成像场强分布的时候可以近似忽略。h(x0,y0;xi,yi)做自相关并归一化即可得到 OTF。因此我们提出了冗余信息提取的方法,冗余信息是指光传输过程中出现其他系统的多余信息,通过提取多余的信息,利用非相干光照明条件下光信息的非定域性质,修正某一区域扭曲的信息。在本研究的例子中,非相干光PSF中-1级衍射区域中存在0级光信息,且误差小。我们将设法将该0级信息提出,重新构造0级衍射区域。利用这一点,将非相干衍射光场转换到相干衍射光场,并在理论上与其对应的相干光照明下的光场信息进行对比修正,再转回非相干光场,并用实际光场修正计算衍射光场;此过程不断循环迭代,直至得到正确的0级信息。
2 X射线闪烁体成像系统
以一种新型的X射线闪烁成像系统为例,对闪烁晶体表面修饰二维光栅阵列,可以突破全内反射的限制,提高光学信息的提取,特别是高空间频率的光学信息[18-19]。提取抑制高频噪声,大大提高信噪比。然而,提取的信息会失真,导致多个虚拟物点,并且具有不同的空间分布,使最终的图像失焦、分散和退化,因此在没有图像恢复的情况下不利于成像。图1(a)是成像系统的对照组的模型图。X射线照射到样品上,X射线通过闪烁体后转换成可见光,最后由CCD成像。图1(b)是成像系统的实验组的模型图,两者的唯一区别是实验组的闪烁体的出射面修饰了二维光栅阵列。

图1 对照组(a)和实验组(b)设备模块图Fig.1 Device module diagram of imaging system(a)Control group,(b)Experimental group
2.1 新型闪烁体成像系统信息冗余
在二维光栅闪烁成像系统中,非相干系统中PSF的-1级衍射包含相干传递函数的-1级衍射和0级衍射信息。将实验组和对照组测得的微孔进行反卷积得到PSF,即对应于OTF的PSF,去掉第0阶中心。以理论结构PSF的0级衍射为初始值。为了实验的方便,我们将PSF简化为一个对称函数,使模型的自相关运算等价于卷积运算。构建点扩散函数计算过程中,迭代次数200次,计算时间大约20 min,迭代之前与迭代之后相同位置的差值的误差在10-5。不断迭代,不断添加正确的信息,直到收敛得到正确的PSF。流程图如图2所示。

图2 冗余信息法构建PSF的流程图Fig.2 Flow chart of constructing point spread function with redundant information method
2.2 新型闪烁体成像系统PSF及图像复原结果
实验数据由上海光源BL13WI线站获得。实验时X射线能量15 keV。成像探测器的CCD像素阵列2 048×2 048,5倍镜头下像素分辨率为1.3 μm×1.3 μm,数值孔径NA=0.5。对照组闪烁体为YAG:Ce,晶体尺寸∅25.4 mm×0.2 mm,双面抛光,折射率1.82,中心发光波长550 nm;实验组闪烁体为同样YAG:Ce闪烁体,但在其表面修饰加工一层二维光栅,周期300 nm,直径180 nm。所用实验样品为脱水斑马鱼样本,微孔大小20 μm。小孔的成像结果、反卷积PSF和冗余信息法得到的PSF在图3中显示。
图4是分别用实验20 μm小孔,反卷积得到的PSF和信息冗余法得到的PSF对斑马鱼进行图像复原得到的效果图。

图3 小孔的成像结果(a),反卷积PSF(b),冗余信息法得到的PSF(c)Fig.3 Imaging results of pinholes(a),deconvolution PSF(b),PSF obtained by redundant information method(c)
在无参考图像质量评价当中,常用的方法是在待评价图像的基础上通过低通滤波器构建一个足够模糊图像(几乎损失所有高频图像纹理细节)作为参考图像;假设它与真实图像做相同滤波后的图像相同;然后对评价图像和参考图像进行各种对比运算,以运算结果评价待评价图像的质量,Q值算法就是其中的一种。Q值算法建立在矩阵的奇异值分解理论(Singular Value Decomposition,SVD)基础上。SVD在图像处理、图像评价和模式识别等领域广泛应用。同一幅图像,经某种处理前后,图像Q值的相对大小具有很强的评价意义。若是处理过后,Q值增大,表示该处理促使图像失真度增加,图像质量变差;若是处理过后,Q值减少,则表示该处理降低了图像的失真程度,尤其是低频部分,这一般是图像的主要信息[20]。表1是斑马鱼的Q值变化,表1中Qorg、Qre分别表示对照图的Q值和复原图的Q值。ΔQ表示复原图相对于对照图的Q值变化率。

图4 斑马鱼对照组图片(a),实验20 μm恢复斑马鱼的细节结果图(b),反卷积得到的PSF恢复斑马鱼的细节结果图(c),冗余信息提取法得到的PSF恢复斑马鱼的细节结果图(d)Fig.4 The picture of zebrafish control group(a),image restored by experiment 20 μm(b),image restored by point spread function obtained by deconvolution(c),image restored by point spread function obtained by redundant information extraction method(d)

表1 采用三种复原方法复原斑马鱼前后Q值的变化Table 1 Changes of Q value before and after zebrafish restoration by three restoration methods
与对照组图像相比,20 μm圆孔作为PSF、实验反卷积PSF和冗余信息法PSF的复原图像噪声水平都有所下降,但是由Q值评价结果可以看出,使用20 μm小孔复原和实验反卷积得到的PSF复原图像Q值下降比较少,而冗余信息法复原图像Q值则下降很多。所以冗余信息法做图像复原处理降低了图像的失真程度,尤其是低频部分,图像的主体信息。信息冗余法恢复的图像信噪比提高更加明显;而且得益于二维光栅的作用,多提取的光子对图像高低频信息起到了增强的作用,由于实验影响因素繁多,所以很难反卷积得到十分精确的系统PSF,故复原误差较大,而冗余信息提取法可以有效地避免这一点,达到良好的复原效果,消除了二维光栅对成像造成的不利影响,保证对照组图像的基本特征的前提下,增强了图像的高低频细节,提高了图像的信噪比。因此冗余信息法复原的图像高低频细节都更加清晰,图像质量更高。
3 结语
本文以一种新型X射线闪烁体成像系统为例,采用信息冗余提取方法构建PSF,成功恢复了受二维光栅影响而退化的成像。信息冗余提取方法利用非相干光照明下光学传递函数-1级衍射光信息冗余来提取0级光信息,不断迭代加入正确信息,最终获得系统的PSF,可以恢复复杂光学系统的成像。本研究从理论和实验上说明了信息冗余提取方法的有效性,且具有较强的适用性。
