基于点源模拟法的体源全能峰符合效率实验研究
2020-01-17张文利屈国普叶芝甫曾德凯
张文利 屈国普 赵 越 汪 伦 叶芝甫 曾德凯
(南华大学 衡阳 421001)
在放射性监测中,监测仪器的探测下限是一个很关键的指标[1],仪器的探测下限取决于本底水平、探测效率、样品量和测量时间等,从探测下限的推导公式可以看出[2],增加测量时间、降低本底水平、增强探测效率和增加测量样品量都可以降低探测下限,但同时需考虑最优化。
目前国内外都习惯采用低本底γ能谱的方法来进行核监测[3],对于存在级联关系的放射源来说,符合测量能大大地降低本底,从而降低探测下限。符合技术是利用电子学的方法在不同探测器的输出脉冲中把有时间关联的事件选择出来。只有偶然符合时,两个探测器才会同时有输出,所以会极大地减少本底计数[4]。
探测效率的获取方式主要有理论计算和实验方法两种。理论计算即准确给出各种参数后,使用蒙特卡罗(Monte Carlo)软件模拟或数值计算γ光子的输运过程来得到体源的探测效率,但是模拟结果具有局限性,不能监测到随着时间和环境的改变而发生的变化。从而进行实验很有必要,而实验方法则是用标准源来直接进行刻度,需要使用已知放射性核素种类和活度的标准体源作为参照,它是γ能谱分析中的基本方法,较为精确,可靠性高。
利用13N作为示踪剂对一回路压力边界进行监测,具有源项能够准确计算、能定量给出泄漏率、响应快等优点。13N是氮核的一种同位素,具有β+衰变放射性,β+粒子与物质相互作用发生正电子湮没效应,发射两个能量为0.511 MeV的γ光子,通过测量光子数量就可以导出一回路水是否泄漏,但是13N的半衰期只有9.96 min,而且需要通过医用加速器制取,从成本和保质期来看都不划算[5]。本实验使用22Na来代替标准源项,提出运用点源模拟法来测量13N的符合效率,以期制定一种13N符合效率的标定方法,便于日后核电厂、研究所等单位13N符合效率的测量。
1 点源模拟法原理
点源模拟法就是根据测量所测区域划分的代表点的全能峰探测效率来模拟出体源的全能峰探测效率。
理论上首先定义坐标系。实验取样容器如图1所示,对5个空腔分别进行编号,空腔内部用于放置各个探测器,正中间放置主探测器,编号为1号探测器,周围逆时针依次为2~5号探测器。Z轴是取样容器的轴线。柱坐标系r是离取样容器轴线的z的距离,θ是r的方位角。
在任意一点(r,θ,z)放置一个标准源,记录单个探测器和两两探测器符合的计数,则该点的真符合计数率为:
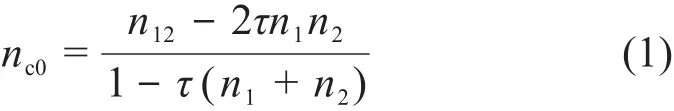
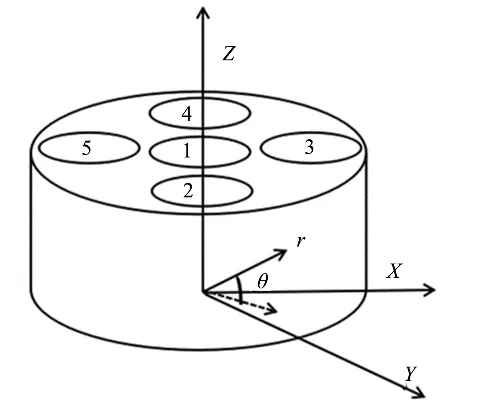
图1 取样容器结构图Fig.1 Structure diagram of sample container
式中:τ为符合分辨时间;n1、n2是单个探测器记录的计数率;n12是这两个探测器符合测量的计数率。当所选点源活度为A时,该点的探测效率为:
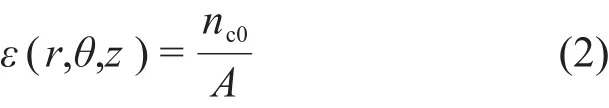
S为体源在XY平面的投影面积,该平面的符合探测效率为:

则体源的符合探测效率为:

2 测量方法
探测系统由探测器、数据处理、数据获取组成,系统单元框图如图2所示。探测器中Na(Tl)闪烁体直径为75 mm,侧面包裹有3.5 mm厚的氧化镁粉末,外表包壳为1.5 mm铝。实验过程中,探测器的低压端接-12 V电压,高压端和信号端分别接到NIM机箱(H1222)上的1 500 V高压电源(BH1283N)以及放大器(BH1218)上,多个探测器输出的信号在经过不同程度的放大之后,分别接到定时单道(FH1007B),再接入符合电路(BH1218)进行符合处理,最后将两两符合和各个输入端的信号分别接到不同的自动定标器(BH1220N),适当调整定标器的工作时间,记录定标器的数值,就完成了数据采集。
调试好所有插件后,首先测量137Cs的能谱图,137Cs全能峰能量为0.331 MeV,使其能谱图峰位道数保持在331道左右,固定此时的电压和放大器倍数;然后测量60Co的能谱图,60Co全能峰能量分别为1.13 MeV和1.32 MeV,能量刻度后进行三点拟合,22Na的全能峰能量为0.511 MeV,拟合得到22Na的全能峰道数为208~308道,对应能量为416~626 keV,即定时单道阈值为2~3 V,符合分辨时间利用符合电路测出为t=0.33 μs。

图2 探测系统单元框图Fig.2 Unit block diagram of detection system
根据符合法的特点[6],设计了此次的取样容器。容器直径有290 mm、300 mm、350 mm、400 mm四种,材料为不锈钢,这里以300 mm为例进行说明,容器内部有5个圆柱空腔用于放置探测器,每个内腔内直径为90 mm,不锈钢厚度为(1±0.1)mm(可忽略壁厚影响),内腔高度(80±0.5)mm,容器总高度为(85±0.5)mm,周围4个圆柱两两轴心相距200 mm,与外围不锈钢最近距离为5 mm,测量主体为中间的不规则空腔,装置上方封有盖子,整个装置处于密封状态,只要任意两个探测器同时有信号输出就认为有一个符合信号。鉴于器材所限,本实验实际测量只使用了两个探测器,如图1所示,对5个空腔进行编号,当测量时,先将探测器分别放置在1、2号位置,记录此时单个探测器和两两探测器符合的计数,然后两个探测器按照组合方式放置位置,(1,2),(1,3),…,(4,5)(不重复),依次改动探测器的位置,记录下共10组数据,然后重复操作下一个点[7]。
实际测量时,首先对取样容器进行区域划分。还是以300 mm为例,先将容器均分为4个部分,按如图3所示进行划区,均分的4个部分中,切线包围的中间区域径向划分为三个等面积的圆扇,然后取径向r=80 mm、115 mm画圆弧,区域内划分为9个部分,测量的时候取中心点,剩下的三个部分也按照此步骤划分区域,共可取52个点(直径为290 mm、350 mm、400 mm的取样容器也需进行类似的区域划分);本次实验为了减短实验周期,只取均分的1/4,也就是13个点(斜切线和圆围成的不规则区域从左到右依次为10、11、12、13,中间部分最内圈从左到右依次为1、2、3;第二圈为4、5、6;最外圈为7、8、9)进行实验测量;最后纵向上分7个平面,容器总高 80,依次测量 2 mm、15 mm、20 mm、40 mm、60 mm、65 mm、78 mm各个高度的平面实验点。
在测量过程中源的固定问题也不可小觑,在此我们采用泡沫能很好地解决这个问题:将泡沫切成合适大小,然后中间刨出一个正好卡住源的合适小槽放置封装源,当需要调整高度时,只需要在下面垫上合适高度的泡沫即可。
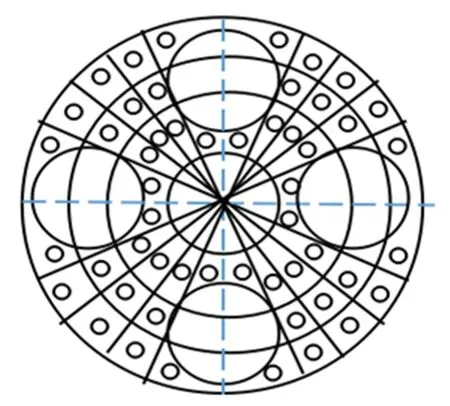
图3 实验取点Fig.3 Experimental measuring points
3 数据处理和结果
3.1 点源的符合效率计算
实验前首先进行本底测量,分别记录下单个探测器的5组数据和两两符合的10组数据,并进行偶然符合处理,代入式(1)中,得到10组符合计数,10组计数率相加等于本底的计数,然后固定好源,重复上述操作,实验结束后,再次进行本底测量,将两次得到的本底计数取平均值,最后将前面得到的符合计数减去本底平均值计数,则等于该点的符合计数。本实验Na源是2001年7月1日购至南华大学,编号505,初始源强 5.79×104Bq,半衰期 2.6 a。实验从2019年3月1日开始测量,源强计算出来为520 Bq,测量时间为100 s,将上述得到的符合计数代入式(2)中,即得到各点的符合探测效率。
3.2 点源符合效率到体源符合效率的转换
根据相关文献[8],式(3)可转换为:
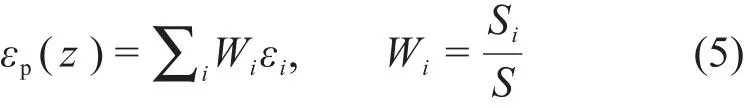
式中:Si为任意部分面积;S为总面积。这里需要注意的是,直径为400 mm和350 mm的取样容器是先做的实验,300 mm和290 mm是后面做的,所以为了实验准确性,源强经过了重新计算,得到结果为490 Bq。
依旧选取直径300 mm的取样容器为例,从2 mm开始,记录所选13个点的数据后,计算出占1/4取样容器的比例情况分别为0.143、0.224、0.304、0.086、0.243,代入式(3)得:(d1+d2+d3)×0.143+(d4+d5+d6)×0.224+(d7+d8+d9)×0.304+(d10+d11)×0.086+(d12+d13)×0.243(d1~d13指各点得的符合探测效率),即可计算出该平面的符合计数率,最后依次代入剩下6个平面13个点的数据,重复操作得到的4个尺寸的各面符合效率,同时注意取样容器直径为290 mm、300 mm时,因容器形状所限,取样高度为2 mm和78 mm只能测量中间部分的少量点,每个点的占比率会比较大,所以会存在较大误差。
根据前面求得的4个尺寸的各面符合效率的数据,我们可以按积分来计算出各个尺寸的符合探测效率,这里采用的方法是:用MATLAB对上述点进行拟合,得到一个多阶多项式,然后代入式(4)即为符合效率,拟合图如图4所示。


图4 MATLAB拟合图Fig.4 MATLAB fitted curves
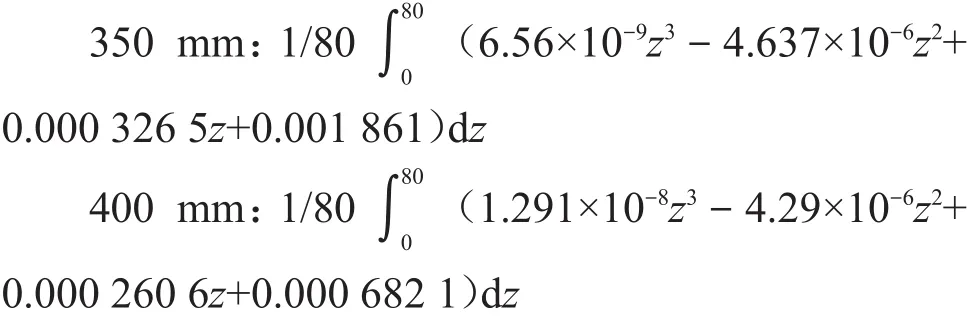
计算出体源的符合探测效率及其与体积的乘积,然后再用Geant4模拟[9]的符合探测效率的数值,进行相应计算[10],对比模拟和实验的结果整理如表1所示,两者的比较值在9.2%以内是一致的,并进一步讨论了符合效率η和取样容器体积V的关系,发现随着取样容器体积V的增大,η与V的乘积会先上升后减小,这一规律和Geant4的模拟结果也是一致的。
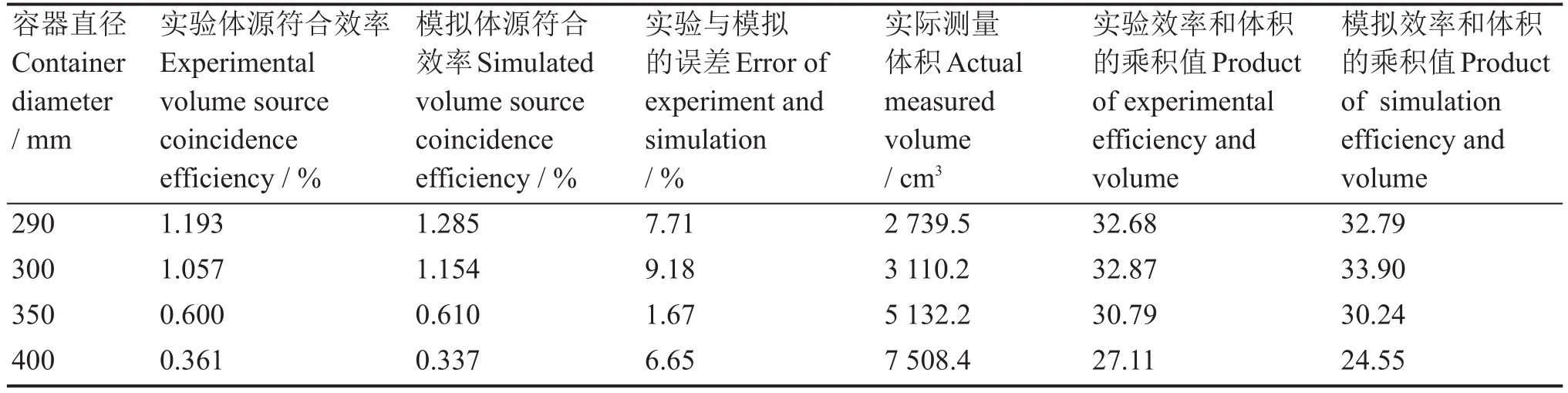
表1 实验结果对比Table 1 Comparison of experimental results
实验的不确定度来源于:源强、计数统计、上下域(±9 keV)、源位置不确定(±1 mm)、本底扣除等,另外取样容器直径为290 mm、300 mm时,取样高度为2 mm和78 mm只能测量中间部分的少量点,每个点的占比率会比较大,所以会存在较大误差。
4 结语
本工作采用学校的标准22Na封装源测量了直径分别为290 mm、300 mm、350 mm和400 mm的取样容器空间中各点的符合探测效率,据此计算出体源的符合效率η,符合效率η的测量值与Geant4的模拟值在9.2%之内一致,即用该法来测量体源的探测效率是存在可行性的,而且简单方便好实现,在今后的放射性监测中,可以根据一回路中长管的直径,将多探头采用文章中的固定方法进行组合安装,并对要测的体源进行区域划分、取代表点测量,依次记录计数值后代入实验公式,就可以求出体源的符合探测效率以查看泄漏情况。此方法可以用于监测核电厂、研究所等单位的泄漏率,提高探测下限。
