过异面四点确定球面方程的策略分析

王成强

(成都师范学院 数学学院，四川 成都 611130)

引言

“解析几何”是大学数学的重要知识模块，对培养学生的空间想象能力、抽象思维能力、科学计算能力等都大有裨益[1-2]. 二次曲面理论是大学数学解析几何知识模块的重难点，每届中国大学生数学竞赛都会涉及对二次曲面理论的考查[3]. 中国大学数学竞赛每年举办一届，试题分为数学专业类与非数学专业类，它们的命题角度新颖，趣味性浓郁，创新性强，具有极高的研究价值[3-4]. 2011年举办的第三届中国大学生数学竞赛预赛试卷的第一题涉及求解一类特殊二次曲面，即球面方程的问题，其完整表述如下：

球面是一类高度对称的二次曲面，其定义可简略表述为空间中到定点的距离等于定值的点的全体. 球面是高中阶段所学的圆周理论的延伸与拓展，而众所周知的是，后者具有丰富的性质，是高中阶段数学学习的重难点，因空间几何的复杂性，空间球面的性质更加丰富，其学习或者相关问题的解答需要更丰富的空间想象能力. 本文旨在以问题(*)为基础，探究空间中过异面四点确定球面方程的策略.

1 三维空间中过异面四点确定球面方程的策略

方法1利用“列标准方程 + 求几何参数”的方法确定球面的方程

设球面S的标准方程为(x-x0)2+(y-y0)2+(z-z0)2=r2. 将点A、B、C、D的坐标代入此方程，得

可发现该方程组等价于

由Cramer法则，得

进一步，还有：

r2=(1-x0)2+(2-y0)2+(7-z0)2=(1-1)2+(2+1)2+(7-3)2=25

综上，球面S的标准方程为：

(x-1)2+(y+1)2+(z-32)=25

方法2利用球面的几何实质确定其方程

设球面的球心的坐标为(x0,y0,z0)，按球面的定义，点A、B、C、D到球心的距离相等，即

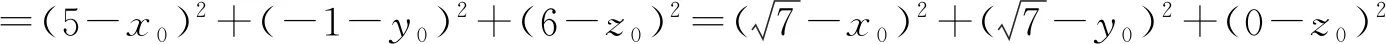
与方法1类似，经整理与化简可得方程组

仿照方法1，利用Cramer法则，经计算可得(x0,y0,z0)=(1，-1，3). 于是，球面S的标准方程为

(x-1)2+(y+1)2+(z-3)2=(x-x0)2+(y-y0)2+(z-z0)2=(1-1)2+(2+1)2+(7-3)2=25

方法3利用球心的特殊几何位置属性确定球面的方程

球面S的球心同时位于下列两条空间直线上：

与

换言之，球面S的球心坐标(x0,y0,z0)满足方程组

仿照方法1，利用Cramer法则，经计算可得(x0,y0,z0)=(1,-1,3). 仿照方法2可完成余下的步骤.

方法4利用球面簇确定球面的方程

以AB为直径的球面方程为

(x-1)(x-4)+(y-2)(y-3)+(z-7)(z-3)=0

或者

x2+y2+z2-5x-5y-10z+31=0

x2+y2+z2-5x-5y-10z+31+λ1(x-3y+5)+λ2(4y+z-15)=0

将点C、D的坐标代入上述方程，得

由Cramer法则，得

于是，球面S的方程为

x2+y2+z2-5x-5y-10z+31+3(x-3y+5)+4(4y+z-15)=x2+y2+z2-2x+2y-6z-14=(x-1)2+(y+1)2+(z-3)2-25=0

即球面S的标准方程为：(x-1)2+(y+1)2+(z-3)2=25

方法5利用“列一般方程+求系数”的方法确定球面的方程

设所求球面的一般方程为x2+y2+z2+ux+vy+wz+f=0. 代入A、B、C、D的坐标，得到方程组

由Cramer法则，得

于是，球面S的标准方程为：(x-1)2+(y+1)2+(z-3)2=25

注1一般地，仿照方法5，可得到三维空间中过异面的四点P1(x1,y1,z1)、P2(x2,y2,z2)、P3(x3,y3,z3)、P4(x4,y4,z4)的球面的方程

经整理，得

方法6利用公式确定球面的方程

经化简整理，有

即球面S的标准方程为：(x-1)2+(y+1)2+(z-3)2=25

2 过空间异面四点确定球面方程与过平面不共线三点确定圆周方程

过空间异面四点确定球面方程与过平面不共线三点确定圆周方程的过程相似.事实上，前文提出的过空间异面四点确定球面方程的六种方法中的思路都适用于过平面不共线三点确定圆周方程. 方法1与方法5可笼统归为方程思想，这类方法在确定平面圆周方程方面有重要应用.例如，为确定过平面不共线三点A(x1，y1)、B(x2，y2)、C(x3，y3)的圆周的方程，应先列出该圆周的标准方程(x-x0)2+(y-y0)2=r2(x0、y0、r待定)或者一般方程x2+y2+2Dx+2Ey+F=0(D、E、F待定)，然后代入点A、B、C的坐标并求出待定参数的值，最后回代参数的值就可得到圆周的方程.方法6的思路(详见注1)也可用于确定平面圆周的方程.事实上，有下述结论成立：过不共线三点A(x1，y1)、B(x2，y2)、C(x3，y3)的圆周方程为

与平面圆周相比，空间球面的几何结构更复杂，几何性质更丰富.例如，在方法3中，为确定过空间异面四点A、B、C、D的球面方程，先利用球心在空间直线段AB、AC、AD、BC、BD、CD的中垂面上这一性质以确定球心的坐标，再计算出点A(B、C或D)到球心的距离，此即为球面半径，综合这两方面信息就可写出球面的方程. 方法3的思路也可用于确定过平面不共线三点A、B、C的圆周的方程：先利用圆心在平面直线段AB、AC、BC的中垂线上这一性质确定圆心的坐标，再计算出点A(B或C)到圆心的距离，此即为圆周半径，综合这两方面信息就可写出圆周的方程. 又如，在方法4中，为确定过空间异面四点A、B、C、D的球面方程，先确定出以A、B为对径点的球面方程F(x,y,z)=0，再确定出平面ABC的方程π1(x,y,z)=0与ABD的方程π2(x,y,z)=0，之后假设球面S的方程为F(x,y,z)+λ1π1(x,y,z)+λ2π2(x,y,z)=0，最后代入C、D找出等量关系，列方程解方程确定出待定参数λ1与λ2，回代参数λ1与λ2的值便得出球面S的方程.方法4的思路在确定平面圆周方程中也有重要应用.为确定过平面不共线三点A、B、C的圆周方程，可先确定以A、B为对径点的圆周的方程G(x,y)=0及直线AB的方程L(x,y)=0，然后设出圆周的方程G(x,y)+λL(x,y)=0，并通过代入点C的坐标求出λ的值，最后回代λ的值便得到圆周的方程.

经前述分析可发现，过空间异面四点确定球面方程与过平面不共线三点确定圆方程周方程，两者的思路与过程都紧密相关，每种用以确定平面圆周方程的思路都可用以探究确定空间球面方程.但是，与过平面不共线三点确定圆方程周相比，过空间异面四点确定球面方程则需要更丰富的空间想象能力与较强的科学计算能力.

3 结语