图的原子键连通性指数的下界

周后卿

(邵阳学院 理学院，湖南 邵阳 422000)

设G= （V,E）是一个具有n个顶点，m条边的简单连通图，顶点集合记为V= ｛1 ,2, … ,n｝，顶点i的度记为di，设图G度序列为｛d1,d2, … ,dn｝.基于图的分子结构描述符(通常称拓扑指数)是刻画分子物理和化学性质、设计药理活性化合物和识别环境有害物质等方面的有用工具[1].因此，研究人员提出了许多这样的图不变量，然而只有少数被证明适用于实际用途，其中之一便是原子键连通性指数(以下简称ABC指数)[2-4]，1998 年分子图的ABC指数被Estrada 等人介绍过.

文献[5]定义了分子图的ABC指数为

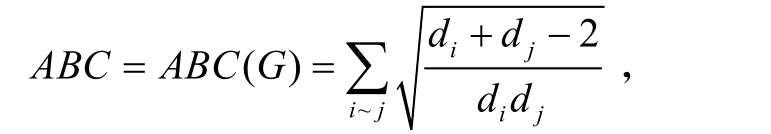
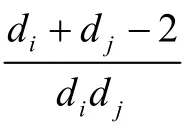
本文只讨论简单连通图和单圈图的ABC指数的下界.

1 几个已知结论及引理

首先简单回顾单圈图的定义.单圈图是只含一个圈的简单连通图，它的顶点数与边数相等.

对于分子图的ABC指数，引进几个已知结论.

在文献[2]中，K C Das 证明了下列结论：

定理A若G是一个具有n个顶点，m条边，最大顶点度为Δ 的简单连通图，则

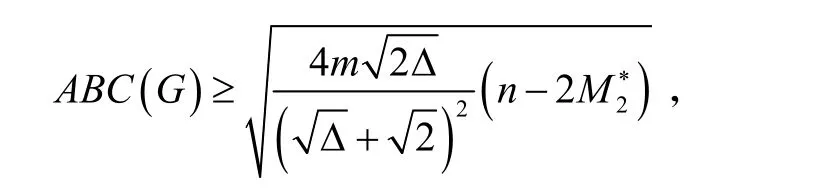
在文献[4]中，B Furtula 等人给出了树的界，得到下列定理：

定理B设T是一个顶点为n的化学树，则

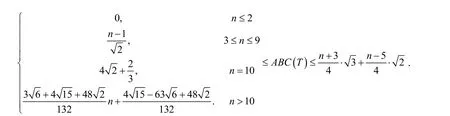
陈锦松等人(见文献[7])证明了：若G是具有n个顶点的单圈图，则

不难看出，文献[7]的这个结论是在文献[4]的基础上做了改良.

现在证明简单连通图的ABC的指数的下界.为了证明定理，需要下述引理.

引理[8]设 0＜a＜a i＜A（i= 1,2, … ,n），则

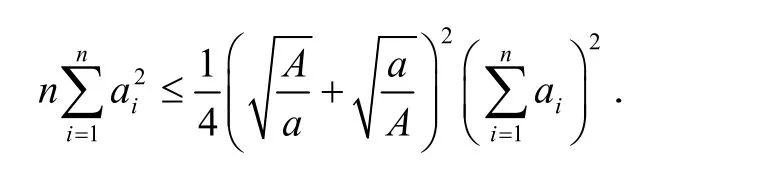
2 主要结论

现在，证明本文的第1 个结论.

证明不妨设图的顶点度d i,dj≤Δ，则

从而有

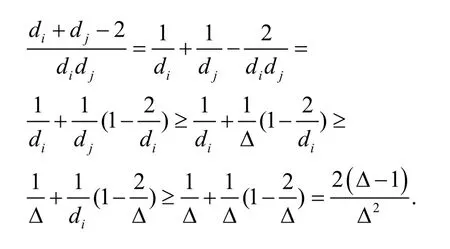
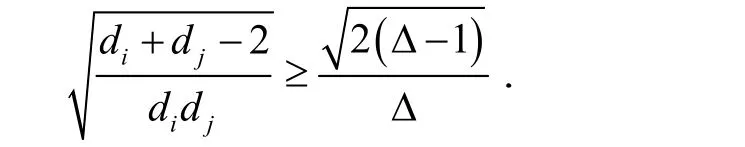
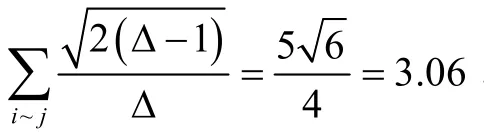
图1 具有5 个顶点的单圈图

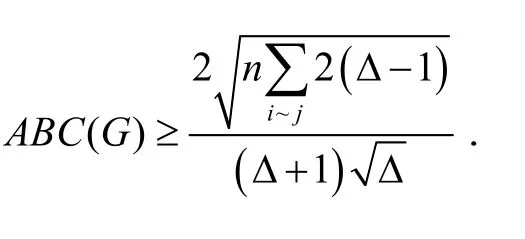
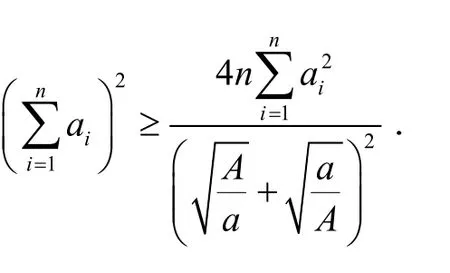
于是有

从而推出

仍以上述单圈图为例，并利用定理2 计算，可得

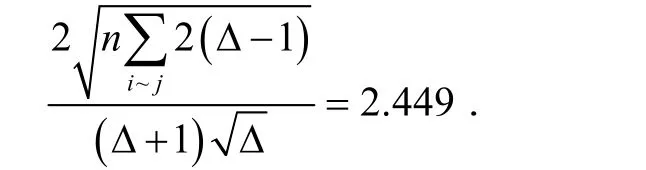
显然，ABC(U5) = 3.85 ＞ 2.449，这说明定理2 成立.

对于单圈图，利用定理A，可推出下列定理.

定理3若Un是具有n个顶点、最大顶点度为Δ 的单圈图，是修正的第2 类Zagreb 指数.则

其证明从略.

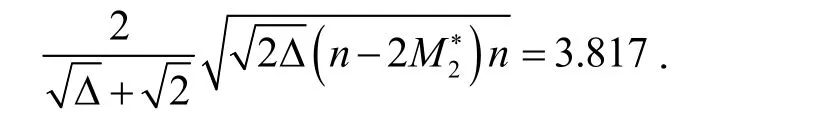
显然，3.85 3.817＞ ，定理3 成立.