模式变换脉冲星PSR J0614+2229的多波段辐射区研究∗

张颜荣，陈建玲，王洪光，黄秀健

(1.广州大学，广东广州 510006；2.运城学院，山西运城 044000；3.华中师范大学，湖北武汉 430079)

PSR J0614+2229(即B0611+22)的自转周期为0.335 s，特征年龄只有9万年，非常年轻，是一颗特殊的模式变换脉冲星。除了像其它一些模式变换脉冲星那样有爆发(Burst，以下简称B模式)和正常(Normal，以下简称N模式)两种不同的辐射状态之外，其脉冲相位也存在同步的偏移，并且模式变换呈现准周期性。

自文[1]于1972年发现这颗星以来，其模式变换行为已被多个团队研究过。1980年，文[2]最早通过单脉冲观测注意到其辐射存在时标为几分钟的变化，在430 MHz，当这颗星的脉冲较强时，其相位常常偏后一些，脉冲轮廓的相位偏移量可达2°左右。1992年NOWAKOWSKI①http：//adsabs.harvard.edu/abs/1992msem.coll..280N通过在相同波段研究，确定它为模式变换脉冲星，模式特征时标为几百秒。两种模式下的脉冲轮廓都为高斯形，但宽度、强度和相位均有差别。2000年KERN②http：//adsabs.harvard.edu/abs/2000ASPC..202..175K发现这颗星的偏振位置角的最大斜率处在脉冲轮廓的尾部边界，由此认为其辐射主要来自脉冲星极冠区的前部区域，而不是充满极冠区；并提出B模式脉冲轮廓更宽是由于存在暂现锥成分的猜测。2014年文[3]通过327 MHz和1400 MHz两个波段在同一天进行的单脉冲观测发现，在327 MHz相位较后的模式明显强于相位较前的模式，而在1 400 MHz两种模式的强度差别不大。此外，他们还通过光谱分析试图寻找子脉冲漂移特征，但两种模式都没有发现子脉冲漂移的证据。2016年，文[4]利用在150 MHz和327 MHz的同时观测，以及在327 MHz和820 MHz的同时观测，发现在150 MHz和327 MHz的B模式相位靠后，而在820 MHz则相反，N模式反而更靠后，认为KERN提出的暂现锥成分假说尽管可以解释B模式脉冲宽度的增加，但无法解释在不同频率上B模式相对N模式的相位变化。

以上研究发现了这颗脉冲星复杂的模式变换行为，但对其模式变换时辐射区域如何变化还没有很好的解释，这很大程度上是由于缺乏多波段同时偏振观测的数据。已有的偏振观测表明，该星的偏振位置角是一条光滑的S形曲线[5-6]，可以用经典旋转矢量模型(Rotating Vector Model，RVM)[7-8]或相对论性RVM模型(RRVM)[9-11]很好地描述，并以此估计辐射高度[9]。但是文献中尚没有对不同模式的偏振位置角和辐射高度进行研究的工作，这正是本文研究的重点。

本文通过分析帕克斯天文台64 m射电望远镜获得的10 cm和50 cm波段同时观测数据以及20 cm波段的观测数据[12-13]，从多个波段考察模式变换时偏振特征的变化，并基于旋转矢量模型对PSR J0614+2229辐射区域的分布和随频率的变化给出新的结果。

1 观测与数据处理

本文使用帕克斯天文台64 m射电望远镜的历史观测数据[12-14]，③http：//data.csiro.au。10 cm，20 cm和50 cm 3个波段的中心频率分别为686 MHz，1 369 MHz和3 100 MHz，所用后端均为宽波段相关处理器(Wide Band Correlator)，采用1 024采样数和1 min子积分时长。在686 MHz和3 100 MHz通过5 010 cm接收机在MJD 53 658.809 26同时观测，观测时长为51 min，有效带宽分别为64 MHz和1 024 MHz，单个通道带宽分别为0.125 MHz和1 MHz。在1 369 MHz通过H-OH接收机在MJD 53 667.808 10进行观测，观测时长为18 min，有效带宽为256 MHz，单通道带宽为0.125 MHz。

脉冲星的原始观测数据为PSRFITS[13]文件，本文使用脉冲星数据处理专用软件包PSRCHIVE[13]，④http：//adsabs.harvard.edu/abs/arXiv：1205.6276处理：(1)把频域两边信噪比很低的通道用paz模块切掉，并对数据进行自动去噪，用pazi模块手动消除频域和时域的射电干扰；(2)利用射电参考源Hydra和噪声二极管的信号对数据用pac模块进行流量定标、偏振校准和pcm定标。(3)对处理后的偏振数据进行偏振位置角的拟合等分析。

2 不同模式辐射高度的计算

2.1 计算辐射高度的方法

计算辐射高度的方法有多种[15]，其中，1991年文[9](以下简称BCW91)提出的相对论性方法是两种常用的方法之一，它用旋转矢量模型来拟合偏振位置角数据，确定最佳拟合曲线的最大斜率点(SGP，Steepest Gradient Point)的相位ϕ0，并计算它与脉冲窗口中心相位ϕc之间的差值，用以下近似关系计算辐射高度r：

其中，Rlc为脉冲星的光速圆柱半径

上述相位差来源于磁层共转引起的相对论性效应——光行差效应和辐射高度与方向不同引起的光程差效应。相比之下，另一种常用方法——通过脉冲宽度和辐射几何关系计算高度的方法没有考虑这些因素，因此，相对论性方法比纯几何方法更接近物理实际。

该方法适用于r＜＜Rlc的情形，优点是计算公式简单，且不像辐射几何方法那样需要得到较为精确的磁倾角α(磁轴和自转轴夹角)和碰撞角β(视线和磁轴夹角)。而这两个参数对辐射几何方法是必须的，虽然它们可以通过对偏振位置角数据进行旋转矢量模型拟合得到，但对于像PSR J0614+2229这样轮廓较窄的脉冲星，所得到的α的误差较大(如BCW91拟合的结果为αBCW91=30°±100°)，因此，用辐射几何方法得到的高度误差较大。而相对论性方法对磁倾角的误差不敏感，所以本文选用这种方法。

基于该方法(即(1)式)，文[9]计算了PSR J0614+2229在1.4 GHz的辐射高度，结果为rBCW91=490±140 km⑤原文中由于将周期误作0.25 s而得到的值为350 km(对应于相位差ΔϕBCW91=7°±2°)。不过这一结果是针对总积分轮廓的，不能回答不同模式时辐射高度的变化。本文已经分别得到了3个频率上B模式和N模式的偏振轮廓，原则上可以利用该方法计算各自的辐射高度，从而检验是否发生了高度变化，以及随频率的变化情况。但是该方法有一个前提假设，即要求辐射区域关于磁轴和自转轴所在平面(以下简称磁轴子午面)对称。经过对比两种模式脉冲窗口中心相位以及偏振位置角曲线最大斜率点的相对移动，可以推断至少有一种模式不满足这一前提假设，因此，不能简单地用(1)式求解。

2008年，文[10]对BCW91的方法做了深入研究，并对(1)式中的相位差给出了更为直观的理解。在r＜0.1Rlc且极冠区满足Gouldreich-Julian电流密度[16]的情况下，将BCW91的相对论旋转矢量模型改写为对惯性观测者参照系(IOF)更加友好的形式：

其中，视线与自转轴夹角ζ=α+β；ϕobs为惯性观测者参照系中观测到的脉冲相位；ϕf为磁轴子午面中辐射高度为0处的脉冲相位(作为参考相位)；Δϕr为高度r处的辐射相对0高度处辐射的相位差(等价于轮廓窗口中心相位相对参考相位ϕf的偏移量)；ψr为该处辐射的偏振位置角；ψΩ为自转轴在垂直视线的平面中的投影角。由于光行差和光程差效应的联合贡献，导致脉冲窗口中心ϕc相对参考相位ϕf移动的相位差为

其中，负号表示窗口中心前移。要保证(1)式成立，则要求最大斜率点的相位ϕ0相对于ϕf后移的值为

也就是说，(1)式中的相位差可以理解为脉冲窗口中心前移和最大斜率点后移共同贡献的结果。

上面两个相位差中，Δϕr依赖于辐射区关于磁轴子午面对称的假设，而Δϕ0不依赖。设想一个简单的对比，一种情况是辐射区在磁轴子午面两侧对称分布，另一种情况是辐射区只在磁轴子午面前面一侧(是前者的一半)，二者辐射高度都相同，那么后者的偏振位置角曲线就是前者的一半。既然偏振位置角形状重合，那么二者的最大斜率点就一样。不过后者轮廓的窗口中心显然比前者更靠前。由此可见，最大斜率点的相位与参考相位的变化量能准确地反映辐射高度，对辐射区不对称的情况也适用。

本文的主要任务是研究模式变换时辐射区高度是否发生变化。由于参考相位是共同的，所以可以利用两种模式下最大斜率点的相位差计算辐射高度之差，再结合脉冲窗口中心相位的差别评估辐射区域偏离对称的情况。采用的步骤如下：

(1)拟合各模式的偏振位置角数据，得到最佳拟合曲线的最大斜率点相位；通过最大斜率点相位差计算各频率上两种模式的辐射高度差。

(2)测量各模式脉冲窗口的中心相位，通过模式间窗口中心相位差以及最大斜率点相位与窗口中心的相位差推断辐射区的变化。

2.2 偏振位置角的旋转矢量模型拟合

原则上拟合偏振位置角数据应该使用相对论旋转矢量模型，不过在r＜0.1Rlc的情况下相对论性旋转矢量模型和经典旋转矢量模型所给出的偏振位置角曲线形状一致，这可以通过对比(2)式和如下经典旋转矢量模型[7-8]函数关系看出：

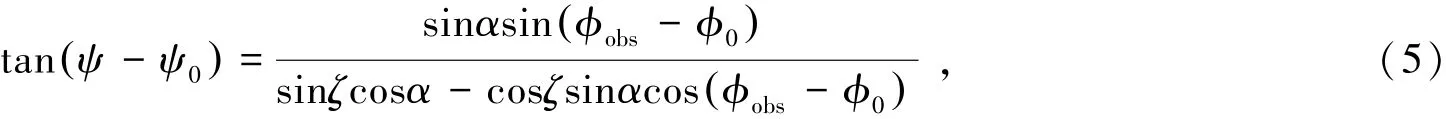
其中，ϕ0和ψ0是磁轴子午面中磁力线上的辐射相位与偏振位置角，ϕ0与(2)式中的ϕf是等价的，同时它也是偏振位置角曲线上最大斜率点的相位，有

因此，为简便起见，本文仍采用经典旋转矢量模型拟合偏振位置角数据。

另一个需要处理的技术问题是上式中的4个参量ϕ0，ψ0，α和β的拟合结果依赖于数据质量。数据质量越高，拟合结果不确定度越小。此外，对于同一颗星的多频辐射和各辐射模式，尽管ϕ0和ψ0可能有变化，但α和β的值应该保持不变。基于这两点考虑，应该选择数据质量最高的偏振轮廓拟合得到α和β，并将其固定，用于各模式的偏振位置角数据的拟合得到ϕ0和ψ0。拟合采用PSRCHIVE中的psrmodel模块，它是在国际天文学联合会协定[17]下编写的基于经典旋转矢量模型拟合4个参数的模块，程序允许同时拟合4个参数，也允许限定部分参数来拟合其它参数。

3个波段的数据中，10 cm和50 cm的观测时间最长，均为1小时，但脉冲星在50 cm的辐射要强得多，因而50 cm数据的信噪比在3个波段中最高，其偏振位置角的误差最小、相位范围最大，这对于得到更可靠的α和β值至关重要。因此，首先选取686 MHz总积分轮廓的偏振位置角数据拟合。得到的结果如图1，具体参数为：α=83.8°±78.9°和β=-6.0°±2.2°，和BCW91在1.4 GHz的结果(在国际天文学联合会协定下[17]，αBCW91=30°±100°和βBCW91=-6°±15°)在误差范围内相吻合。从图1可以看出，最佳拟合旋转矢量模型曲线和偏振位置角数据符合得很好。本文得到的偏振位置角的最大斜率点大约在轮廓的最右侧边界处，这和KERN的结果一致。接下来就可以将上面得到的α和β值用来拟合3个波段不同模式下的ϕ0和ψ0。

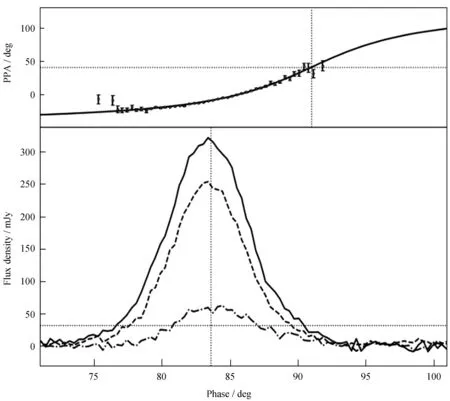
图1 686 MHz上偏振位置角的旋转矢量模型拟合。顶部图框中实线为旋转矢量模型的最佳拟合曲线，虚线交叉处为最大斜率点 (ϕ0，ψ0)。底部图框分别用实线、短划线以及点划线给出了总轮廓I、线偏振L和圆偏振V，同时用虚线标出了总积分轮廓的窗口中心所在相位和10%峰值流量水平Fig.1 RVM fit of the PPA data at 686MHz.The top panel shows the best-fit RVM curve， with the SGP(ϕ0， ψ0)being denoted by the cross section of the vertical and horizontal dotted lines.The bottom panel shows the total intensity(I，solid)， linear polarization(L， dashed)， circular polarization(V， dash-dotted)， the central phase of the profile′s window determined at the 10%level of the pulse peak(vertical dotted line)and the 10%level of the peak intensity(horizontal dotted line)of the averaged pulse profile

2.3 两种模式的辐射高度

通过肉眼辩别剔除各波段数据中可能包含两种模式的子积分(通常是在从一个模式的序列变到另一个模式的序列时过渡的子积分)，并将剩余的两种模式的数据分开并叠加得到各自的总轮廓，然后对两种模式的偏振位置角进行拟合，结果如图2，其中最大斜率点相位分别用蓝色(B模式)和红色(N模式)的虚线表示。从图2可以看出，从B模式变换为N模式时，脉冲轮廓和偏振位置角的最大斜率点相位都发生了明显的向右偏移，并且最大斜率点相位的偏移量呈现出随频率逐步增大的特征。当把N模式偏振位置角的最大斜率点和B模式的对齐后(黄色和绿色)，两者的偏振位置角数据吻合得非常好，这说明磁场的几何位形没有改变。

图2 两种模式线偏振位置角的旋转矢量模型拟合。顶部图框：蓝色和红色分别代表最大斜率点对齐之前的B模式和N模式数据，绿色和橙色的点分别代表最大斜率点对齐后的B和N模式数据。底部图框：以峰值强度10%水平确定的两种模式的轮廓窗口中心。各类点和线型的意义与图1相同Fig.2 The RVM fit for the PPAs of the two modes.Top panel：the blue and red curves show the best-fit RVM curves of the B and N modes without aligning the SGPs，while the green and orange points and curves represent those with the SGP alignment.Bottom panel： the centers of averaged pulse profiles′window determined at the 10%level of the pulse peak.The meanings of the data points and the line types are the same as those in Fig.1

表1给出了每个波段上两种模式ϕ0和ψ0的最佳拟合值、它们之间的相位差δϕ0=ϕ0，B-ϕ0，N=Δϕ0，B-Δϕ0，N和高度差δr=rB-rN(二者的关系遵从(4)式)， 以及轮廓窗口中心的相位ϕc和两种模式之间的窗口中心相位差δϕc=ϕc，B-ϕc，N= Δϕr，B- Δϕr，N， 其中下标 B 和 N 分别代表对应的模式。 轮廓窗口中心相位测量的方法是通过取每个轮廓两侧强度等于轮廓峰值强度10%所在相位(如图2)为脉冲窗口的边界⑥10%峰值宽度能够涵盖绝大部分的脉冲相位，相比50%峰值宽度更能代表脉冲窗口。若采用50%宽度，则反映的是辐射区中较强的区域，但是受到脉冲轮廓形状的影响，50%强度的脉冲窗口和10%的窗口未必同时关于磁轴子午面对称，记为L10和R10，脉冲窗口的中间相位为ϕc=(L10+R10)；单侧相位的误差可以用公式e得到，其中σ(Ioff)代表噪声区域强度的标准方差，导出量的误差通过误差传递公式计算。计算中用到了脉冲星的光速圆柱半径Rlc=1.6×104km。

表1 两种模式的相位差与高度差Table 1 The phase offset and the difference in altitude between the two modes

表中负的δϕ0值表示N模式的最大斜率点相位比B模式的更靠后，对应于负的δr值，表示N模式辐射高度比B模式的高。若两种模式的辐射区都对称，由于(3)式和(4)式反号，则δϕc应该为正值，这就要求B模式的轮廓窗口中心要比N模式的滞后，但观测结果恰好相反，这说明(3)式成立的前提——辐射区关于磁轴子午面对称不可能对两种模式同时成立。

为了解释观测N模式轮廓窗口中心滞后的现象，理论上存在3种可能的组合，(1)如果B模式的辐射区是对称的，那么N模式的辐射区就不对称，且位于磁轴子午面后侧的部分要比前侧更宽；(2)如果N模式的辐射区是对称的，那么B模式的辐射区就不对称，且在磁轴子午面前侧的部分比位于后侧的部分更宽；(3)两种模式的辐射区都不对称，但是要求B模式的辐射区比N模式更靠前。

第1种和第2种情况下至少有一种模式的辐射区被假设为对称，这可以方便地计算高度。对第1种情况，测量3个波段下B模式的最大斜率点和轮廓窗口中心的相位差ΔϕBCW，B=ϕ0，B-ϕc，B(等式右边的两个相位值见表1)，并用(1)式计算辐射高度，然后利用表1中的高度差计算N模式的辐射高度。用同样的办法也计算了第2种情况下的两种模式的高度。结果如表2。综合表1和表2可以看出，两种模式之间的高度差随频率递增，但是具体到每种模式的高度随频率的变化关系却存在不确定性：在假设B模式的辐射区是对称的情况下，B模式的辐射高度随频率递减，而N模式却是微弱递增；若假设N模式的辐射区是对称的，则两种模式的辐射高度都随频率递减。

最后，为了方便对比，参照BCW91计算了各频率下累积脉冲总轮廓(两种模式混合)的偏振位置角曲线最大斜率点和轮廓窗口中心相位差累积脉冲轮廓ΔϕBCW，T和辐射高度rT(如表2)。从结果看，总积分轮廓得到的辐射高度随频率呈现递减的趋势，高度值更接近被假设为辐射区对称的那种模式(第1种情况下的B模式或第2种情况下的N模式)。

表2 脉冲星PSR J0614+2229不同模式的辐射高度Table 2 The emission heights of PSR J0614+2229 for different modes

3 结 论

本文利用2005年帕克斯天文台在10 cm，20 cm和50 cm 3个波段的偏振观测数据，对年轻脉冲星PSR J0614+2229模式变换时的辐射区磁场结构和辐射高度可能的变化进行了研究。通过使用旋转矢量模型对B模式和N模式的偏振位置角数据进行拟合，发现两种模式的偏振位置角数据参照最佳拟合模型曲线平移对齐后能够很好地互相吻合，表明在模式变换时脉冲星磁场结构保持不变。根据确定辐射高度的相对论性方法以及3个波段上N模式偏振位置角曲线的最大斜率点相位相对于B模式的滞后量，计算了两种模式高度之差在70±40 km到270±150 km之间，且随着频率增加而递增。在相对论性旋转矢量模型框架下，测量得到的两种模式脉冲窗口的中心相位之差并不能与它们的最大斜率点相位差相自洽，因此，可以推断这两种模式的辐射区并不都关于磁轴子午面对称分布。但受限于数据的信噪比，本文没有对脉冲窗口变化对应的辐射区经度范围的变化进行讨论，有待进一步的偏振观测获得更高质量的多频(或超宽带)观测数据。