基于WIM的江苏省高速公路桥梁汽车荷载模型

宗周红 薛 程 杨泽刚 袁微微 夏叶飞

(1东南大学土木工程学院， 南京 211189)(2中国路桥工程有限责任公司， 北京 100011) (3江苏华通工程检测有限公司， 南京 210005)

公路桥梁汽车荷载模型是通过数学方法对通行的汽车荷载进行抽象、提取以及归纳得到的能够反映汽车荷载特性的计算模型[1-3]，确定公路桥梁汽车荷载的方法主要包括外推法和随机模拟法2种.

外推法依据短期实测汽车荷载效应外推设计基准期汽车荷载效应，得到汽车荷载标准值[4].应天益[5]利用佛开高速公路2周的动态称重( WIM) 数据，采用 Rice 外推理论计算了不同跨径、不同桥型、不同截面在不同重现期下的车辆荷载效应极值，并与规范计算值进行对比；许肇峰等[6]选取广东省5条高速公路WIM系统获取的数据，得到车辆荷载模型作用下的活荷载效应均为规范荷载作用下的1.4倍左右； 李植准等[7]提出基于GPD模型的短期实际汽车荷载效应极值尾部拟合方法，实现对基准期汽车荷载效应极值的估计；Crespo-Minguillón等[8]提出了一种考虑影响因素不确定性的桥梁车辆荷载整体性分析模型，推导了模拟连续交通流量及由短期荷载效应最大值外推长期荷载效应最大值的算法.

随机模拟法通过实测通行车辆参数(如车身质量、车长、轴质量、轴距、车间距等)，得到其概率分布函数，建立随机车队模型并施加于桥梁影响线上，获取汽车荷载效应，进而得到汽车荷载模型标准值.宗周红等[9]基于京沪高速新沂河大桥断面 WIM 数据，得到不同重现期下的汽车荷载效应极值分布；王磊等[10]应用平衡更新过程理论得到车辆荷载效应概率模型；Srinivas等[11]和Chen等[12]分别使用Copula函数研究车辆各轴质量之间的相关性；Chen等[13]运用元胞自动机仿真模拟技术推导出真实交通流下车辆荷载的随机模型；Obrien等[14-15]提出了随机车流对桥梁破坏能力的破坏指数；郭彤等[16]通过对京沪高速公路交通荷载状况的统计分析，提出了车辆荷载多峰分布概率模型，获得了用于剩余可靠度评估的各类车辆荷载评估值；宗周红等[17-19]针对连续梁桥和斜拉桥，研究了异常运行(并道或拥堵)状态下的汽车荷载模型.

中国幅员辽阔，区域经济发展不尽相同，各地公路运输存在显著的差异，因此有必要制定适合区域交通特征的公路桥梁汽车荷载标准.本文依据动态称重系统物联网提供的高速公路通行车辆参数(如车型、车身质量、车间距、轴质量、轴间距等)进行概率统计分析，利用随机模拟方法建立随机车队模型，采用影响线加载的方法，计算出多种桥梁汽车荷载效应，并建立汽车荷载效应极值的概率分布模型.取0.95分位值与规范汽车荷载效应进行对比，建立江苏省高速公路桥梁汽车荷载模型.

1 江苏省高速公路桥梁WIM系统物联网

目前，江苏省全省境内多条高速公路均已安装WIM系统，形成了覆盖全省的WIM系统物联网(见图1和图2).为全面了解江苏省当前汽车荷载特性，选取各WIM系统监测断面尽可能多的数据，列于表1.由表可知，选取数据的时间段基本覆盖了一年四季，汽车总数超过5.4×107辆.相对于烈士河大桥、永安河大桥和锡澄运河大桥而言，新沭河大桥、灌河大桥、新沂河大桥3个监测断面的日均数量略小.

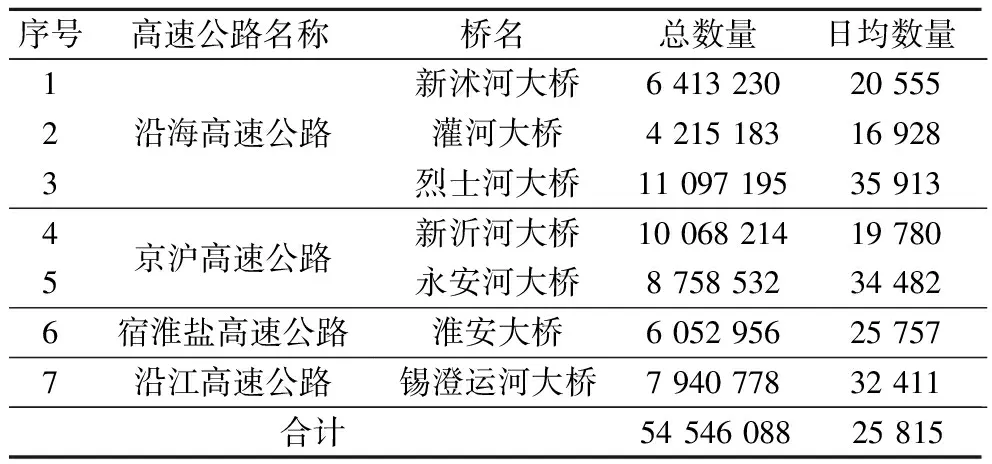
表1 获取WIM监测数据辆

2 汽车荷载特性统计分析

2.1 车型

车型按照汽车轴数分为二轴车、三轴车、四轴车、五轴车、六轴车等5类.由于WIM系统在识别客、货车时存在误差，故二轴车未区分客和货车.七轴车及以上因为所占比例较少，也未考虑.车型比例见表2.由表可知：① 南北走向的沿海高速公路(G15)上货车略多于京沪高速公路(G2)；② 东西走向的宿淮盐和沿江高速公路上货车较南北走向的京沪和沿海高速公路少，南部的沿江高速公路上货车略少于北部的宿淮盐高速公路；③ 全部监测断面上二轴车和六轴车所占比例约为76%和15%；④ 部分监测断面如新沭河大桥、灌河大桥及新沂河大桥上六轴及以上车辆占25%以上，重车所占比例较高，以新沭河大桥、灌河大桥为例，靠近连云港，钢铁、煤炭等运输较多，体现了较为突出的区域交通运输特征以及日益增长的物流运输特色.

2.2 车身质量

为了比较各监测断面同一车型车身质量分布的差异，绘制了全部监测断面上同一车型核密度图(见图3).由图可知，选取0.1和0.9分位点为主要范围上、下限，二轴车车身质量为0.7～6.8 t，均值为2.8 t，多为二轴客车；三轴车车身质量为6.3～23.8 t，均值为14.5 t；四轴车车身质量为9.5～36.7 t，均值为22.6 t；五轴车车身质量为10.1～47.5 t，均值为26.8 t；六轴车车身质量为16.8～60.8 t，均值为39.4 t.最新超载标准《整治公路货车违法超限超载行为专项行动方案》(交办公路[2016]109号)规定，二轴车辆车身质量和货物质量超过18 t、3轴车辆车货总质量超过27 t、四轴车辆车货总质量超过36 t、五轴车辆车货总质量超过43 t、六轴及以上车辆车货总质量超过49 t等5种情形应认定为超限超载车辆，平均超载率为7%.根据各监测断面不同车型车身质量的分布特点，采用混合高斯或混合威布尔概率分布拟合车身质量分布，并进行K-S检验，确定各监测断面上不同车型车身质量的分布类型及参数.

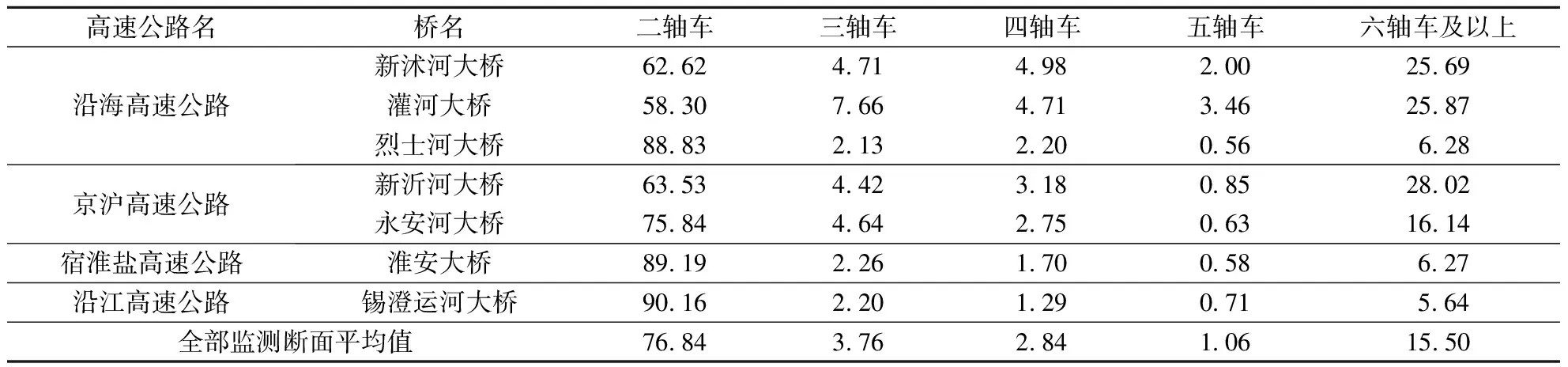
表2 车型比例统计 %

2.3 轴质量

为比较各监测断面同一车型各轴质量分布的差异，绘制了全部监测断面上同一车型各轴质量核密度图(见图4).由图可知，二轴车的2个轴质量基本相等，均值约为2 t，质量占比均值分别为51.11%和48.89%.三轴车轴质量占比均值分别为25.33%、25.43%、49.24%，第1、2轴质量基本相等，为2～7 t，第3轴质量为2～15 t.四轴车质量占比均值分别为19.28%、21.28%、26.91%、32.52%，第1、2轴质量基本相等，为2～7 t，第3、4轴质量也基本相等，为2～15 t.五轴车轴质量占比均值分别为18.38%、27.33%、18.27%、17.36%、18.66%，第1、2、3轴质量基本相等，为2～12 t，第4轴质量为2～8 t，第5轴质量为2～16 t.六轴车轴质量均值分别为12.74%、14.19%、20.27%、17.75%、17.10%、17.95%，第1轴质量为2～8 t，第2轴质量为2～12 t，第3、4、5轴质量基本相等，为2～15 t.

2.4 轴距

不同车型轴间距的抽样过于复杂且意义不大，可利用汽车荷载数据回归分析的不同车型轴间距进行简化.二轴车轴距均值为3.1 m.三轴车第1、2轴轴距均值为2.2 m，第2、3轴轴距均值为4.5 m.四轴车第1、2轴轴距均值为2.2 m，第2、3轴轴距均值为5.0 m，第3、4轴轴距均值为1.3 m.五轴车第1、2轴轴距均值为3.4 m，第2、3轴轴距均值为6.7 m，第3、4轴轴距均值为1.8 m，第4、5轴轴距均值为1.3 m.六轴车第1、2轴轴距均值为2.6 m，第2、3轴轴距均值为1.9 m，第3、4轴轴距均值为7.0 m，第4、5轴轴距均值为1.3 m，第5、6轴轴距均值为1.3 m.

2.5 车间距

车间距对于汽车荷载效应有着重要影响.根据汽车车队的运营特性，可将其分为一般运行状态和密集运行状态.一般运行状态是指道路的通常运行状态，可以直接反映实际汽车荷载的总体水平；密集运行状态主要考虑车流量大、道路出现拥堵或者并道行驶等特殊状态，实际出现的概率较小，在WIM系统安装位置出现的概率近乎为零，在此主要考虑一般运行状态.一般运行状态下车间距和各监测断面实际车间距的概率密度分布见图5.由图可知，实际车间距远大于规范一般运行状态车间距，各监测断面车间距存在较小差异，北中部的灌河大桥、永安河大桥车间距较密，南部的锡澄运河大桥车间距较疏.此外，不同监测断面的车间距概率分布不同，可采用对数正态分布来拟合车间距分布，并进行K-S检验，得到各监测断面车间距分布及参数.

3 汽车荷载特性模拟

车辆荷载具有显著的区域交通特征和季节变化特征.本文抽取了江苏省4条高速公路7个监测断面的动态称重(WIM)监测数据，具有一定的区域交通特征.为考虑实际通行车辆的季节变异特性，保证外推数据具有较好的可信度，选择1 a的监测数据进行分析.按照年度监测数据进行模拟抽样，采用Monte-Carlo法模拟出每个监测断面约25 815×365 =9 422 475≈942×104(各监测断面年均汽车数量)辆汽车的荷载特性值，全省总共7×9 422 475≈6.6×108辆汽车的荷载特性值.

3.1 车身质量

根据各监测断面不同车型实际车身质量分布，采用Monte-Carlo法模拟出相应的车身质量.以新沂河大桥为例，其模拟与实测结果对比见图6.由图可知，模拟车身质量与实际车身质量吻合较好.

3.2 车间距

根据各监测断面的实际车间距分布，采用Monte-Carlo法模拟出相应的车间距数，部分监测断面结果见图7.由图可知，模拟的车间距与实际车间距吻合较好.

4 汽车荷载效应计算

基于Monte-Carlo法模拟得到约6.6×108辆汽车的车身质量、车间距等基础性数据.根据2.3节中的轴身质量比例，可计算出每辆汽车的轴身质量，进而得到每辆汽车的特性值包括轴身质量、轴距、车间距等.将监测断面顺序和车型顺序随机重组，以模拟随机车队.

根据经验，中小跨径桥梁的汽车荷载效应更容易出现超载现象.为使统计分析更具一般意义，主要考虑10、20、30、40 m简支梁桥以及10、20、30、40 m跨径二～六跨连续梁桥等的汽车荷载效应，包括跨中弯矩、支点弯矩和支点剪力等.模拟随机车队汽车荷载效应的计算是将随机车队加载到影响线上，车队每前进0.1 m，计算一次汽车荷载效应.将车队和影响线信息编成2个单列矩阵，行间距设为0.1 m，再进行逐行矩阵相乘.

为便于与规范进行比较，将模拟随机车队汽车荷载效应与规范汽车荷载效应之比K作为统计对象，即K=R/Rs，其中R和Rs分别为模拟随机车队汽车荷载效应和规范汽车荷载效应.模拟随车车队汽车荷载效应计算的车队长度达到365×4.6×107≈1.7×1010m，矩阵长度达到1.7×1011，影响线最大长度为40×6=240 m，矩阵长度为2 400.不计Matlab循环、判断、读取等命令，单计算命令达到1.1×1016次，计算量巨大，采用4台Dell工作站进行计算，CPU内存占用90%以上，持续耗时45 d才得以完成.

5 汽车荷载模型

5.1 汽车荷载效应比日最大值分布

《工程结构可靠性设计统一标准》(GB 50153—2008)[20]中规定，可变作用的标准值由可变作用在设计基准期T内最大值概率分布的统计特征值确定，故汽车荷载标准值的确定需要100 a汽车荷载的最大值分布.然而，获取数据的时间长度有限，无法获得足够多的效应比年最大值，故本文采用与规范类似的处理方法，将效应比年最大值分布替代为效应比日最大值分布，各桥型各效应比日最大值分布见图8.由图可知，各桥型各效应比日最大值分布总体结果偏大，究其原因在于车辆动态称重系统本身的监测误差，动态称重系统给出的车身质量数据存在10%左右的正向误差(即动态称重实测车身质量偏大10%左右)，此外，由于路面不平度等的影响，车辆冲击系数大约为1.05(主要针对中小跨径的混凝土桥梁)，两者合计起来会导致监测车辆荷载的样本存在15%左右的误差.相同跨径简支梁桥的跨中弯矩比通常要大于连续梁桥.相同跨径连续梁桥的跨中弯矩比和支点弯矩比随着跨数的增多而减小，跨径越小越明显，但无论跨径如何，到五、六跨及以上时该规律均不再明显.10、20 m跨径和30、40 m跨径的连续梁桥支点剪力比分布存在明显差别，简支梁的支点剪力比随跨径的增大而增加.

5.2 汽车荷载模型

对于混合全部桥型跨中弯矩比，经K-S检验，其分布不拒绝广义极值分布，获得日最大值分布后，取0.95分位值可得初始荷载效应比Ko=1.45，考虑WIM系统误差和冲击系数15%，可得折减后的荷载效应比Kf=1.26.对于混合全部桥型支点弯矩比，经K-S检验，其分布不拒绝广义极值分布，获得日最大值分布后，取0.95分位值可得初始荷载效应比Ko=1.80，考虑WIM系统误差和冲击系数15%，可得折减后的荷载效应比Kf=1.57.选择30、40 m跨径桥梁的支点弯矩比，经K-S检验，其分布不拒绝广义极值分布，获得日最大值分布后，取0.95分位值可得初始荷载效应比Ko=1.55，考虑WIM系统误差和冲击系数15%，可得折减后的荷载效应比Kf=1.35.

单一种效应比的日最大值分布极有可能是片面的.根据实际桥梁设计经验，可将跨中弯矩比、支点弯矩比、支点剪力比按照50%∶25%∶25%的权重进行混合，经K-S检验，其分布不拒绝广义极值分布(见图9).分布参数为ξ=0.200 794，σ=0.088 826 9，μ=1.319 23，概率密度函数式为

(1)

分布函数式为

(2)

获得日最大值分布后，取0.95分位值可得加权后的初始荷载效应比Ko=1.68, 考虑WIM系统误差和冲击系数15%，可得加权后的折减荷载效应比Kf=1.46. 因此，根据实测汽车荷载数据，建议适用于江苏省高速公路桥梁的汽车荷载取我国现行规范《公路桥涵设计通用规范》(JTG D60—2015)公路-Ⅰ级汽车荷载中的车道荷载的1.46倍.

6 汽车荷载效应折减系数

6.1 横向折减系数

目前，多车道横向折减方法主要包括总效应折减和车道荷载折减2种.总效应折减是指，对于多车道桥梁设计的荷载布置，通常以各车道上同时出现最不利荷载为原则，求得的内力结果再进行折减，以考虑各车道同时出现最不利荷载的概率.美国AASHTO规范和我国规范都采用总效应折减.车道荷载折减即以最不利荷载产生的车道荷载为基础，其余车道进行折减，欧洲规范采用车道荷载折减[4].本文采取总效应横向折减系数，计算得到一车道、二车道、三车道、四车道、五车道、六车道的横向折减系数分别为1.20、1.00、0.85、0.72、0.60、0.47.由表3可知，车道总数小于等于5时，根据我省实际汽车荷载数据计算出来的横向折减系数比规范数值略大，车道数大于5时，比规范略小，这主要是由于假设分布不同，数据高尾部分的累积分布函数斜率不同所导致.

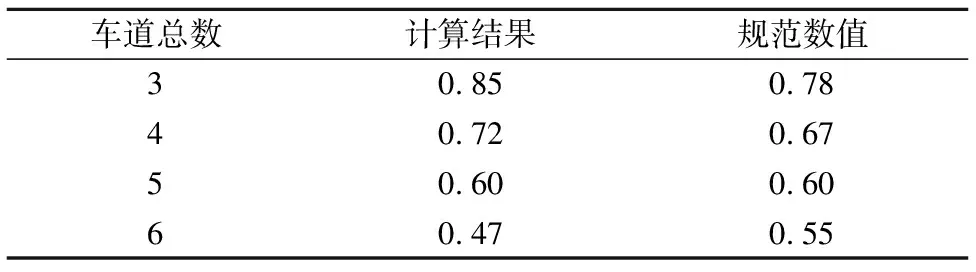
表3 横向折减系数

6.2 纵向折减系数

参照我国规范JTG D60—2015[2]，纵向折减系数的计算主要考虑跨径对效应的影响，采用跨径为100、200、400、600、800、1 000、1 250、1 500 m的虚拟简支梁桥和中跨跨径为100、200、400、600、800、1 000、1 250、1 500 m，跨径比为0.8∶1∶0.8的三跨虚拟连续梁桥的效应影响线，虚拟简支梁桥效应考虑跨中弯矩和支点剪力，虚拟连续梁桥效应考虑跨中弯矩和支点弯矩.通过建立全部效应比日最大值概率分布模型，计算设计基准期内最大值概率分布，再取0.95分位点值，将100 m跨径桥梁的效应比作为基准值进行转换，即可得到折减系数随跨径的变化，结果见表4.由表可知，纵向折减系数随跨径增大而减小的趋势较规范更明显，规范纵向折减系数偏于保守.

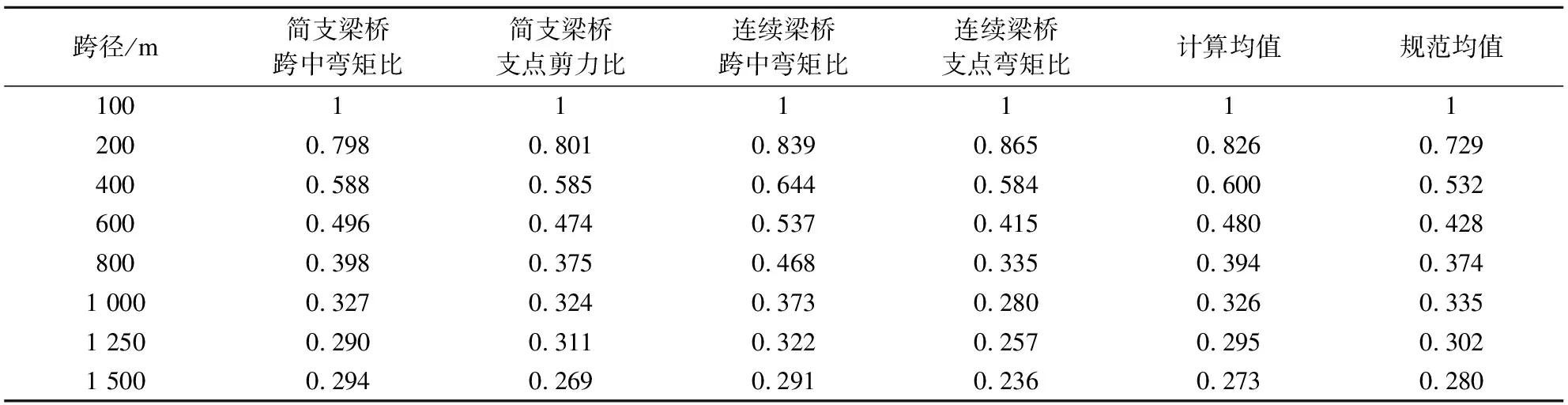
表4 纵向折减系数

7 结论

1) 根据江苏全省高速公路汽车荷载数据可知，二轴车和六轴车及以上平均比例分别约为76%和15%，各监测断面结果差异较大，具有显著的地域交通特征.

2) 各监测断面各轴车车身质量服从混合高斯或混合威布尔概率分布，二轴车车身质量均值为2.8 t，三轴车车身质量均值为14.5 t，四轴车车身质量均值为22.6 t，五轴车车身质量均值为26.8 t，六轴车车身质量均值为39.4 t，平均超载率为7%.

3) 各监测断面各轴车轴质量和轴间距分布差别不大，实际车间距服从对数正态分布，远大于规范一般运行状态车间距.

4) 根据实测汽车荷载数据，建议适用于江苏省高速公路桥梁的汽车荷载取我国现行规范《公路桥涵设计通用规范》(JTG D60—2015)公路-Ⅰ级汽车荷载中的车道荷载的1.46倍.

5) 根据实测汽车荷载数据，计算得到一车道、二车道、三车道、四车道、五车道、六车道的横向折减系数分别为1.20、1.00、0.85、0.72、0.60、0.47.根据实测实际汽车荷载数据计算出来的纵向折减系数随跨径增大而减小的趋势较规范更明显，规范纵向折减系数略偏保守.