基于回旋曲线的垂直泊车轨迹规划与跟踪控制

张家旭 赵 健 施正堂 杨 雄

(1吉林大学汽车仿真与控制国家重点实验室, 长春 130011)(2中国第一汽车集团有限公司智能网联开发院, 长春 130011)(3浙江亚太机电股份有限公司, 杭州 311200)

近几年，无人驾驶汽车成为汽车行业研究的热点，我国和欧美日等主要汽车厂商正在加速布局无人驾驶技术，而全自动泊车系统是无人驾驶汽车的重要组成部分，可以有效解决复杂狭窄泊车环境下的自动驾驶问题，提高泊车过程的便捷性和安全性.因此，现阶段研究开发全自动泊车系统对布局无人驾驶技术具有重要意义[1-2].

全自动泊车系统包括环境感知、控制策略和人机交互3部分，而控制策略是全自动泊车系统的核心，目前国内外学者和汽车厂商对全自动泊车系统控制策略的研究成果可以分为人工智能法和规划-跟踪控制法.文献[3]将提高泊车精度和缩短泊车时间作为优化目标，采用演化策略对基于模糊逻辑规则建立的泊车控制器参数进行优化，文献[4]则采用蚁群算法优化基于模糊逻辑规则建立的泊车控制器参数.文献[5]将熟练驾驶员的平行泊车、垂直泊车和斜向泊车试验数据作为训练样本，并基于遗传算法优化模糊泊车控制器的隶属度函数，实现3种泊车应用场景的全自动模糊控制.文献[6]将熟练驾驶员的泊车试验数据作为训练样本，建立基于自适应神经模糊推理系统的泊车控制策略，实现特定应用场景的全自动泊车控制.人工智能法需要依靠大量的专家数据或控制经验数据建立控制规则库，增加了工程实现难度.

相对于人工智能法，规划-跟踪控制法不依赖专家数据或控制经验，具有较强的工程实现价值.文献[7]综合考虑车辆避碰约束与非完整性约束，规划出一簇平行泊车路径和斜向泊车路径，随后采用模糊逻辑系统选出最优泊车路径.文献[8]建立不规则泊车场景的轨迹规划的数学模型，并通过高斯伪谱法将其转化为非线性规划问题，在统一的优化框架下实现泊车路径与泊车速度的并行规划.文献[9]采用圆弧-回旋曲线组合方式规划曲率连续的平行泊车路径，并基于参考泊车路径的弧长直接将参考泊车路径曲率映射为车辆的等效前轴转角，实现参考泊车路径的跟踪控制.文献[10]综合考虑车辆运动学约束、车辆性能参数约束和泊车避障约束等，以泊车时间最短为性能指标，建立了泊车路径规划最优控制问题的数学模型，并采用高斯伪谱法将泊车路径规划最优控制问题离散化为非线性规划问题，最后采用非线性规划求解器SNOPT求解得到参考泊车路径.文献[11]基于B样条理论和微分平坦理论规划参考泊车路径，并采用模型预测控制方法设计参考泊车路径跟踪控制律.文献[12]综合考虑可行性、安全性、平顺性和工效性4大性能指标，基于车速无关的离散车辆运动学模型提出了平行泊车和垂直泊车最优轨迹决策算法，并分别采用前馈加反馈的控制方式与模糊控制方式实现了方向盘转角和车速的跟踪控制.

本文采用规划-跟踪控制架构，综合考虑汽车运动学约束、避障约束和边界条件约束，提出一种基于回旋曲线的垂直泊车轨迹规划与跟踪控制方法.首先，选择垂直泊车轨迹的弧长作为关联参考量，将垂直泊车轨迹规划问题解耦成路径规划问题和速度规划问题，进而将三维空间内的规划问题简化为2个二维空间内的规划问题，降低垂直泊车轨迹规划的难度.针对垂直泊车路径规划问题，基于回旋曲线规划曲率连续的垂直泊车路径；针对垂直泊车速度规划问题，基于五次多项式曲线规划满足过程和边界约束条件的垂直泊车速度.随后，选择垂直泊车轨迹的横向位移量作为非时间参考量，将垂直泊车轨迹跟踪控制问题解耦成垂直泊车路径跟踪控制问题和垂直泊车速度跟踪控制问题，降低垂直泊车轨迹跟踪控制的难度.考虑垂直泊车轨迹跟踪控制系统的计算时延，以航迹推算算法计算输出的当前车辆位姿和速度为基础，采用预估模型预测下一采样时刻的车辆位姿和速度，将其作为垂直泊车路径跟踪控制问题和垂直泊车速度跟踪控制问题的状态反馈量.针对多输入的垂直泊车路径跟踪控制问题，基于2增益控制理论设计非时间参考泊车路径跟踪2增益控制律，提高垂直泊车路径跟踪控制的鲁棒性.针对多输出的泊车速度跟踪控制问题，基于PID控制设计泊车速度跟踪控制律，实现驱动系统和制动系统的平滑切换控制.最后，结合硬件在环试验平台对所提出的垂直泊车轨迹规划与跟踪控制方法的可行性和有效性进行验证.

1 垂直泊车轨迹规划

1.1 垂直泊车路径规划

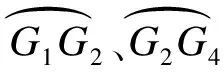
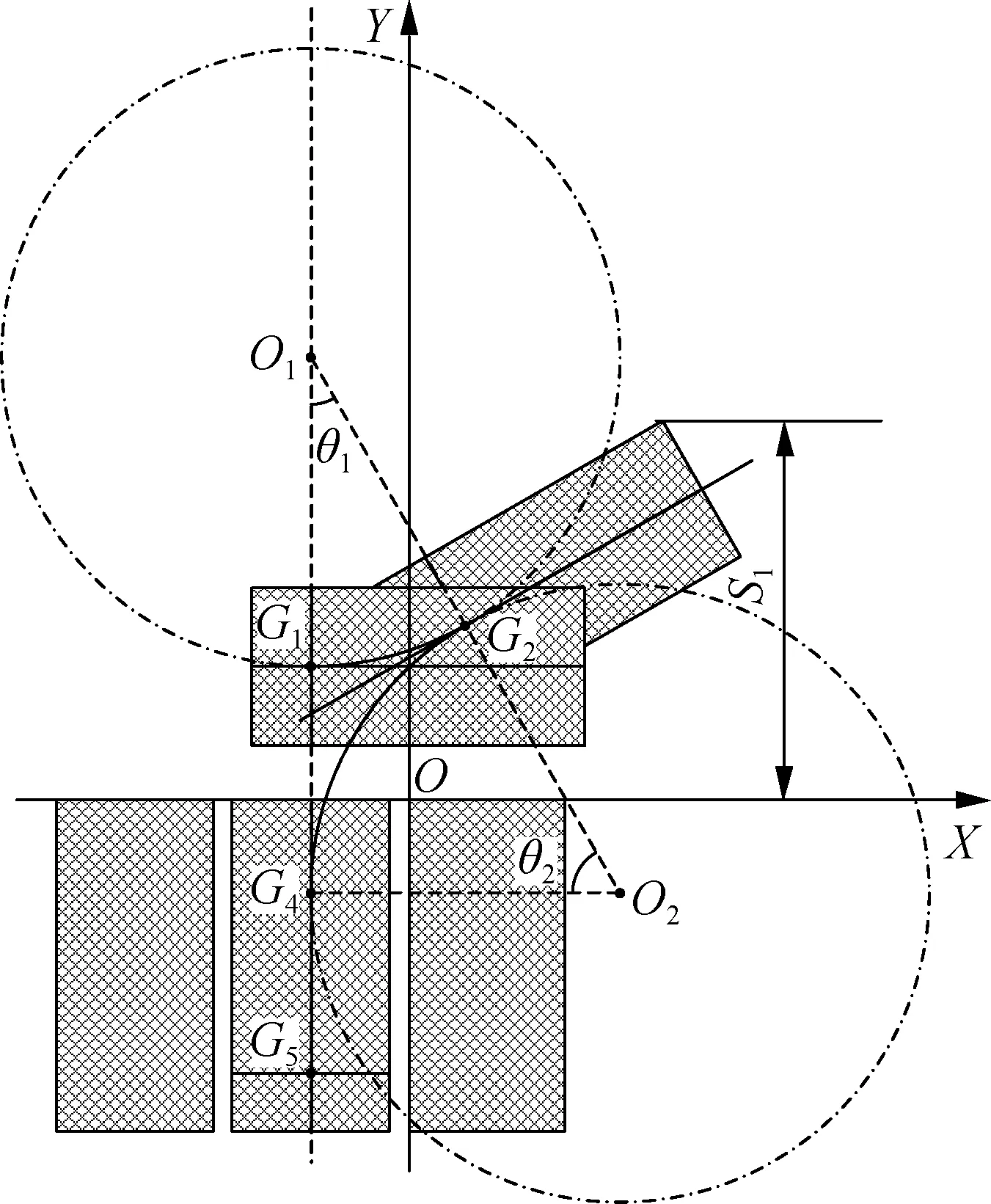
图1 垂直泊车路径规划

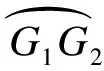
① 计算θ1，即

(1)

② 计算点G2的坐标(xG2,yG2)，即

(xG2,yG2)=(xG1+Rminsinθ1,yG1+Rmin(1-cosθ1))

(2)

③ 计算点G4的坐标(xG4,yG4)，即

(xG4,yG4)=(xG1,yG2-Rminsinθ2)

(3)

(xO1,yO1)=(xG1,yG1+Rmin)

(4)

(xO2,yO2)=(xG4+Rmin,yG4)

(5)

⑥ 计算S1，即

(6)

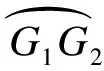
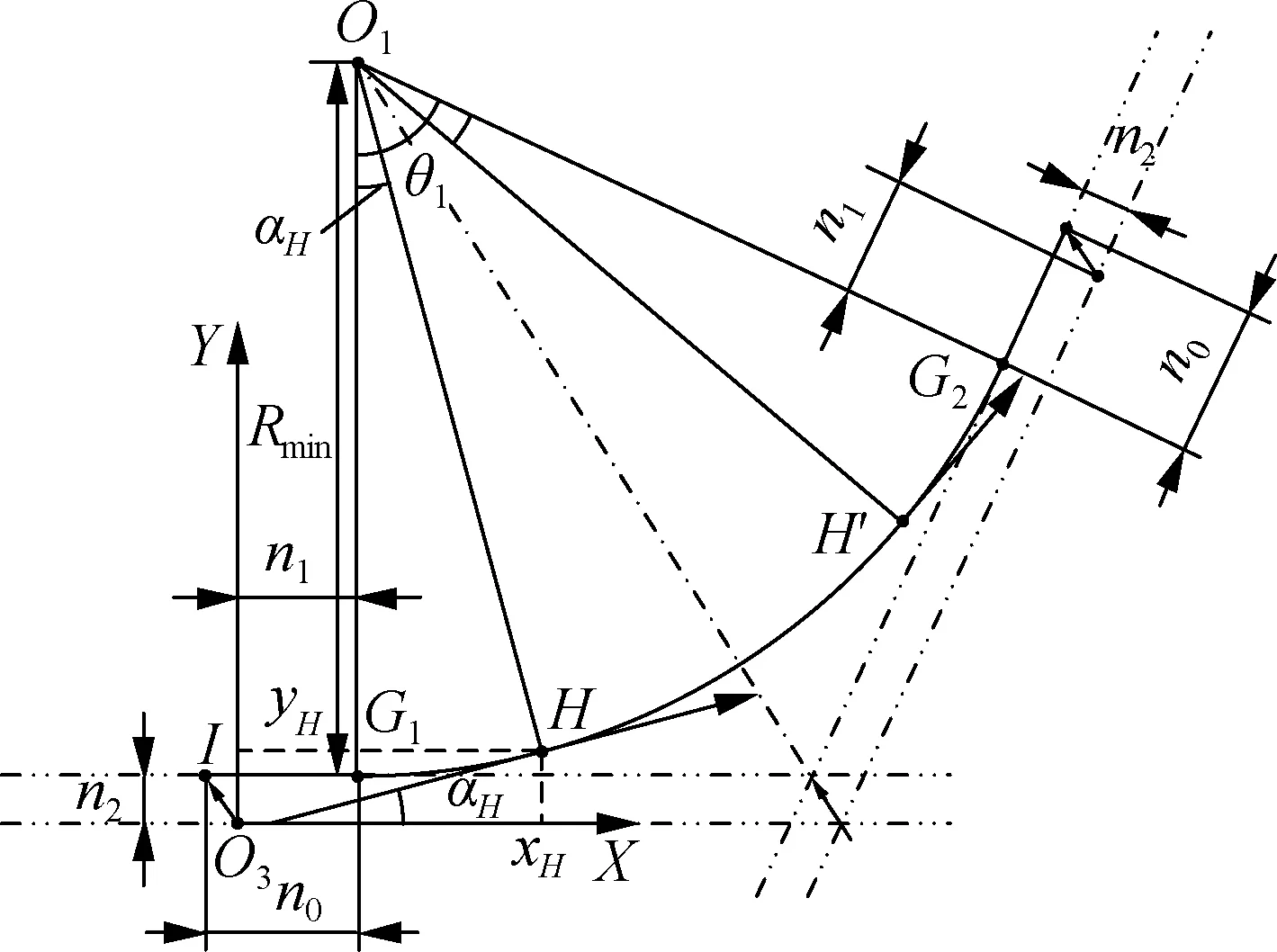
图2 基于回旋曲线的泊车路径平滑原理图

由回旋曲线定义可知，原点O3到点H的回旋曲线长sH=1/(Rminc).由此，基于sH可得

(7)

(8)

(9)

式中，N为回旋曲线的近似阶次.

由式(7)～(9)可得

(10)

式中

n1=xH-RminsinαH

(11)

n2=yH-Rmin(1-cosαH)

(12)

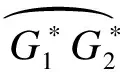
(13)

(14)

② 计算点G0的坐标(xG0,yG0)，即

(15)

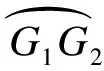
(16)

(17)

(18)

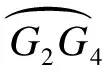
(19)

⑥ 计算平滑之后曲线的端点G3的坐标(xG3,yG3)，即

(20)

⑦ 为了提高垂直泊车路径规划方法的实时性，离线计算并存储回旋曲线的采样序列，通过旋

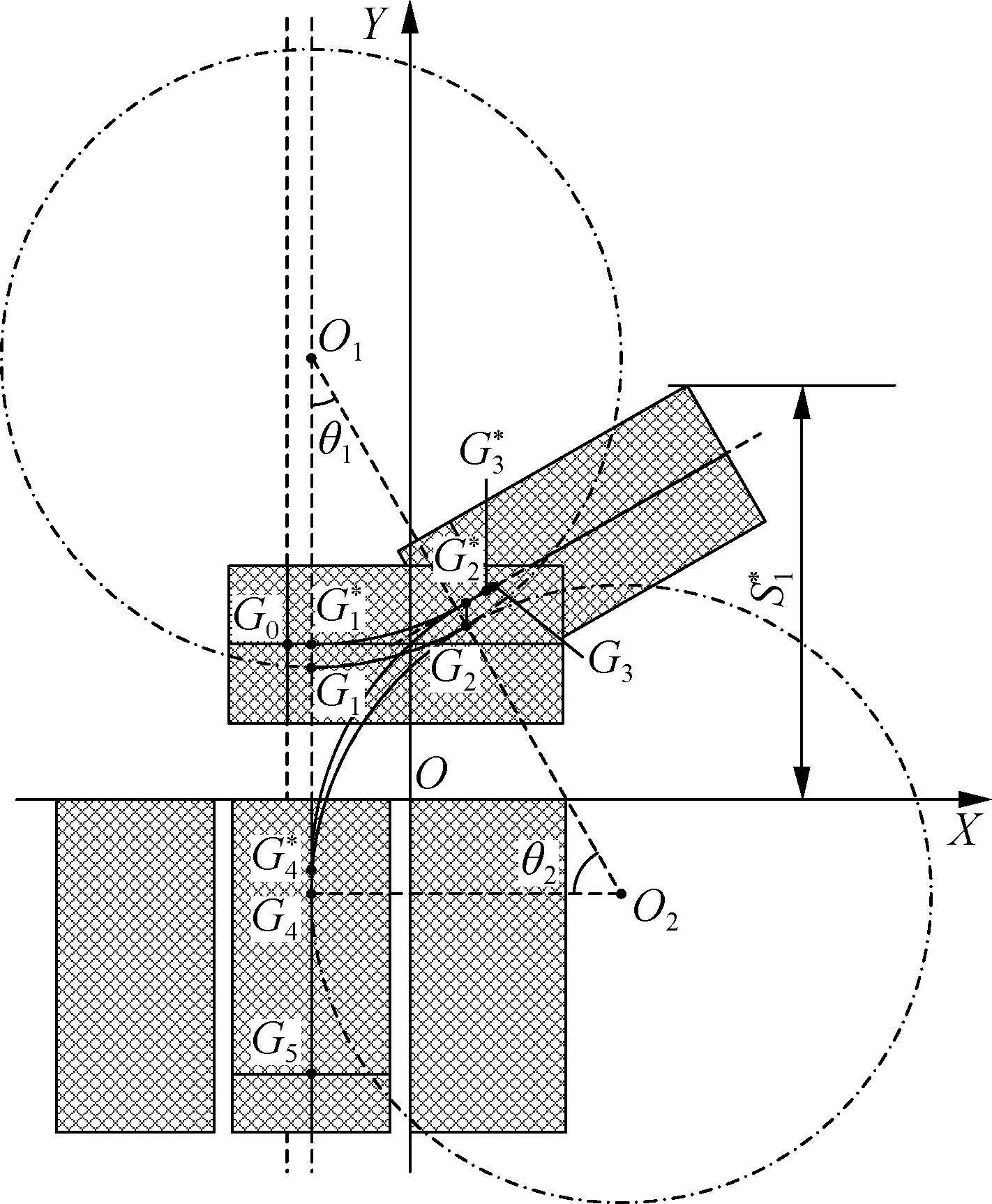
图3 垂直泊车路径平滑

(21)

1.2 垂直泊车速度规划

垂直泊车速度规划的任务是设计满足要求的垂直泊车速度曲线，使汽车从静止开始沿着规划好的路径行驶到目标点，并安全平稳地停在目标点.因此，垂直泊车速度曲线可以分为从零加速到恒定值的加速段、保持恒定值的匀速段和从恒定值减速到零的减速段.本节基于五次多项式曲线设计垂直泊车速度曲线的加速段和减速段，提高垂直泊车效率和舒适性.

由于通过对垂直泊车速度曲线的加速段垂直翻转和水平移动可以得到垂直泊车速度曲线的减速段，因此本节仅需设计垂直泊车速度曲线的加速段.采用五次多项式对加速段的速度曲线、加速度曲线和加加速度曲线分别进行描述，即

v(t)=q0+q1t+q2t2+q3t3+q4t4+q5t5

(22)

a(t)=q1+2q2t+3q3t2+4q4t3+5q5t4

(23)

j(t)=2q2+6q3t+12q4t2+20q5t3

(24)

式中，v(t)、a(t)、j(t)分别为垂直泊车速度曲线加速段的速度、加速度、加加速度；q0、q1、…、q5为五次多项式的待确定系数；t为时间参数.

考虑垂直泊车速度规划的任务需求以及车辆制动系统和驱动系统的机械约束，以最小化垂直泊车速度曲线加速段所需的时间tf作为性能指标，将垂直泊车速度规划问题转化为如下的非线性优化问题：

s.t.vstart=0

vend=vmax

astart=aend=0

|v|≤vmax

|a|≤amax

|j|≤jmax

(25)

式中，vstart和vend分别为垂直泊车速度曲线的起始速度和终止速度；astart和aend分别为垂直泊车速度曲线的起始加速度和终止加速度；vmax、amax、jmax分别为垂直泊车速度曲线的速度最大值、加速度最大值、加加速度最大值.

针对式(25)描述的非线性优化问题，可以采用内点法进行求解[14].

为了提高垂直泊车速度规划方法的计算实时性，对垂直泊车速度曲线的加速段进行离线计算并采样，通过垂直翻转和水平移动变换得到垂直泊车速度曲线减速段的采样点，并且将加速段和减速段的采样点以表格的方式存储在控制器内.由于垂直泊车速度曲线的加速段与减速段是固定不变的，二者所需要的垂直泊车路径弧长也是固定不变的.因此，可以通过调整垂直泊车速度曲线的匀速段时间使得垂直泊车速度曲线与时间轴围成的面积等于垂直泊车路径弧长，即建立所规划的垂直泊车速度与垂直泊车路径之间的对应关系.

2 垂直泊车轨迹跟踪控制

图4 垂直泊车轨迹跟踪控制框图

2.1 垂直泊车路径跟踪控制

垂直泊车路径跟踪控制的任务是设计控制律，使得车辆可以快速、精确、稳定地跟踪参考泊车路径.由于车辆在垂直泊车过程中处于低速大转角行驶状态，可以忽略轮胎的侧向滑动，进而可以采用如下车辆运动学方程描述垂直泊车过程中的车辆行驶状态[15]：

(26)

式中，(x,y)为车辆后轴中点坐标；v为车速；φ为车辆方位角；δd为前轴等效转角.

当车辆倒车时，选择车辆后轴中点的横坐标值的负数作为非时间参考量.考虑参数不确定性、外界干扰等因素产生的系统复合干扰，将式(26)转化为如下包含系统复合干扰的泊车路径跟踪偏差方程：

(27)

式中，x1=yr-y；x2=-(tanφr-tanφ)；yr、ρr和φr分别为参考泊车路径的纵坐标值、曲率和方位角；d为系统的复合干扰.

针对系统式(27)，构造如下的变量变换：

(28)

式中，υ为虚拟控制输入.

定义系统的性能输出z为

z=[z1z2]T

(29)

基于式(29)定义的系统性能输出，设计非时间参考泊车路径跟踪2增益控制律，并得到如下定理.

定理1针对系统式(27)，设计如下非时间参考泊车路径跟踪2增益控制律：

(30)

式中，γ为增益系数，且γ>0.当d≠0时，闭环系统是有限增益2稳定的；当d=0时，闭环齐次系统是渐近稳定的.

证明定义李雅普诺夫候选函数

(31)

对式(31)两端求导数，即

(32)

选取υ=-z1/2，并将其代入式(32)，可得

(33)

增广李雅普诺夫候选函数

(34)

对式(34)两端求导数，即

(35)

将式(30)代入式(35)，可得

(36)

对式(36)两侧进行积分运算，可得

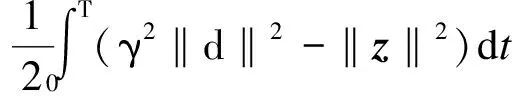
(37)

式中，T为积分时间.

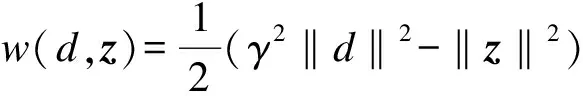
(38)

当车辆前进时，选择车辆后轴中点的横坐标值作为非时间参考量.修正定义x2=tanφr-tanφ，基于上述方法得到控制律与式(30)相同.

2.2 垂直泊车速度跟踪控制

垂直泊车速度跟踪控制需要协调驱动系统和制动系统来实现参考泊车速度的快速、精确、稳定的跟踪控制.由于难以建立被控对象的精确数学，基于PID控制设计垂直泊车速度跟踪控制律，即

uk+1=uk+KP(ek+1-ek)+KIek+1+
KD(ek+1-2ek+ek-1)

(39)

式中，uk+1和uk分别为k+1时刻和k时刻的控制量；KP、KI和KD分别为比例、积分和微分系数；ek+1、ek和ek-1分别为k+1时刻、k时刻和k-1时刻的速度偏差.

为了实现驱动系统和制动系统的平滑切换控制，当uk+1≥0时，uk+1作为驱动系统的基础控制量；当uk+1<0时，uk+1作为制动系统的基础控制量[18].

2.3 车辆位姿和速度预估

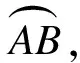
(40)

式中，Tr为后轴轮距.

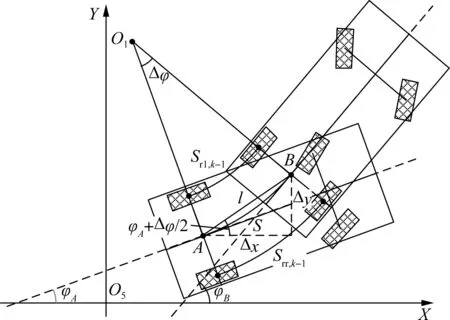
图5 航迹推算法示意图

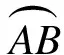
(41)

由此，可得Δx和Δy的表达式为

(42)

将式(40)描述的车辆方位角增量和式(42)描述的车辆后轴中点位置增量累加求和，可得一段时间内的车辆位姿描述，即

(43)

假设车辆后轴中点的速度在k-1时刻到k时刻时间间隔保持不变，可得车辆后轴中点在k时刻的速度vk，即

(44)

由式(43)和(44)可知，已知k-1时刻的车辆位姿与k-1时刻到k时刻时间间隔的车辆右后轮和左前轮走过的距离，可以推算出k时刻的车辆位姿和车速.下面基于k时刻的车辆位姿、车速、前轴等效转角期望值和实际值，预估k+1时刻的车辆位姿和车速.

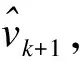
(45)

将车辆转向机构视为一阶惯性环节，并采用前向差分方法离散化，可得

(46)

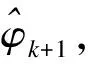
(47)

由式(42)可得k+1时刻车辆后轴中点位置的估计值，即

(48)

由式(45)、(47)和(48)可知，已知k时刻的车辆位姿、车速、前轴等效转角期望值和实际值，可以预估出k+1时刻的车辆位姿和车速.

3 硬件在环试验验证

采用图6所示的硬件在环试验平台对所提出的垂直泊车轨迹规划与跟踪控制方法的可行性和有效性进行验证.

图6 硬件在环试验平台

如图6所示，硬件在环试验平台由上位机、实时处理器1、实时处理器2和超声波雷达台架组成.实时处理器1上运行所提出的垂直泊车轨迹规划与跟踪控制模型，实时处理器2上运行车辆动力学模型和超声波雷达模型，并且实时处理器1和实时处理器2通过光纤进行通信.上位机通过以太网与实时处理器1和实时处理器2相连，实现对实时处理器1和实时处理器2的管理.超声波雷达台架通过硬线与实时处理器1和实时处理器2相连，实时处理器2通过硬线激励真实的超声波雷达传感器，实时处理器1通过硬线接收真实超声波雷达感知到信息.综上，通过上位机、实时处理器1、实时处理器2和超声波雷达台架组成垂直泊车轨迹规划与跟踪控制方法的虚拟仿真验证环境.

在垂直泊车验证工况中，设置车辆长度、宽度和轴距分别为4.155、1.645和2.405 m，车辆前悬和后悬长度分别为0.800和0.950 m，车辆最大泊车速度、最大泊车加速度和最大泊车加加速度分别为1 m/s、2 m/s2和3 m/s3，车辆后轴中点最小转弯半径为4.200 m，硬件在环试验平台仿真步长为1 ms，路面附着系数为1，垂直泊车位宽度和长度分别为2.300和4.155 m，垂直泊车起始点坐标为[-1.378, 2.000]m，试验结果如图7～图10所示.

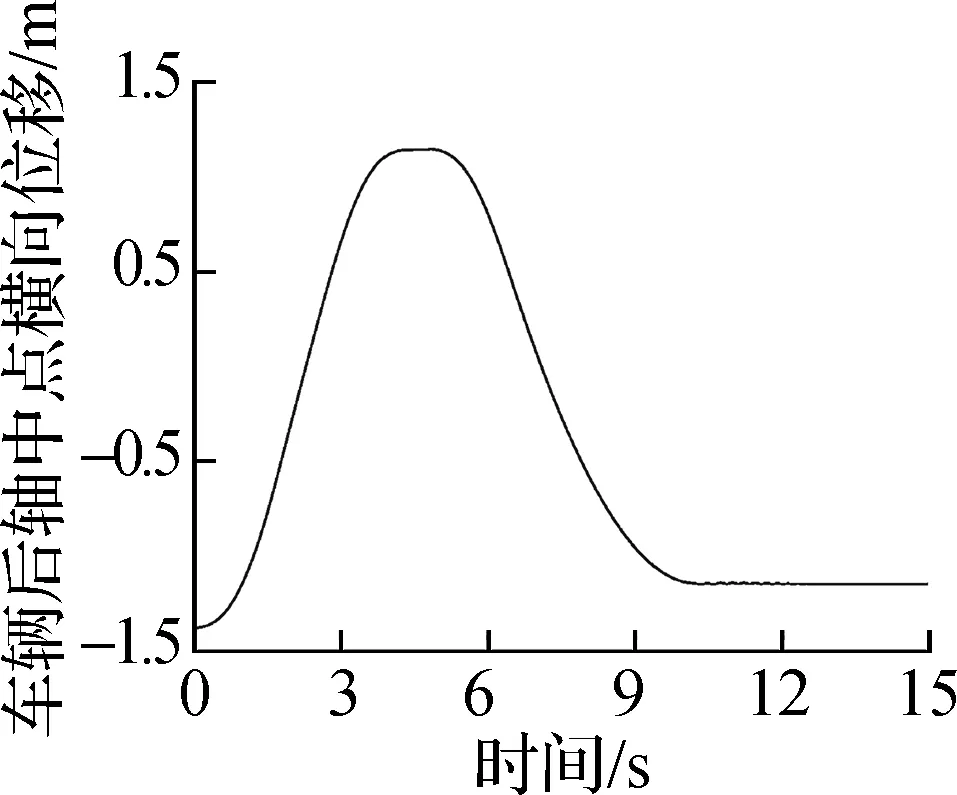
(a) 车辆后轴中点横向位移

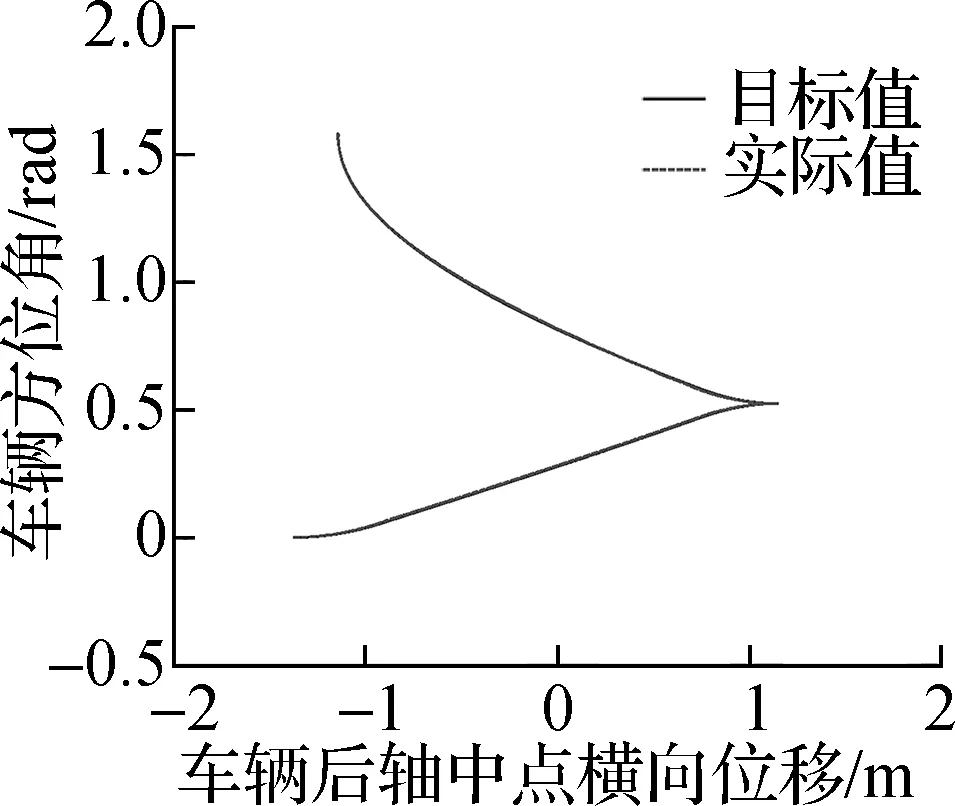
(b) 车辆方位角沿后轴中点

横向位移变化

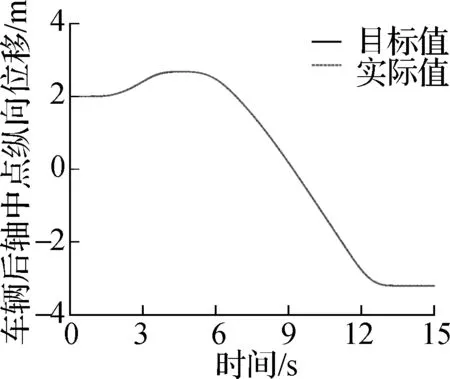
(c) 车辆后轴中点纵向位移

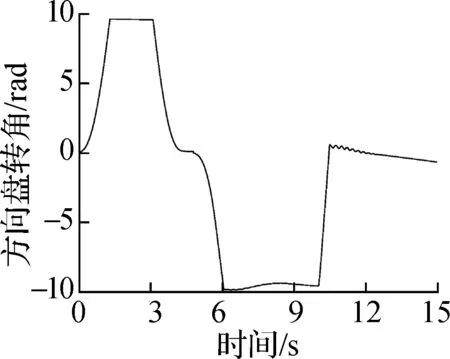
(d) 方向盘转角

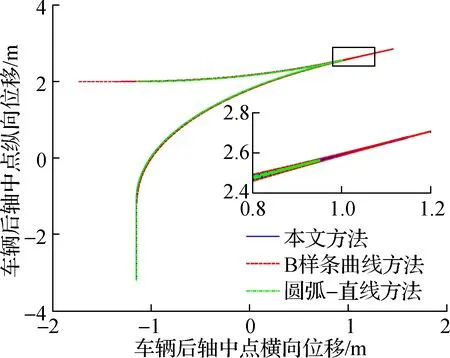
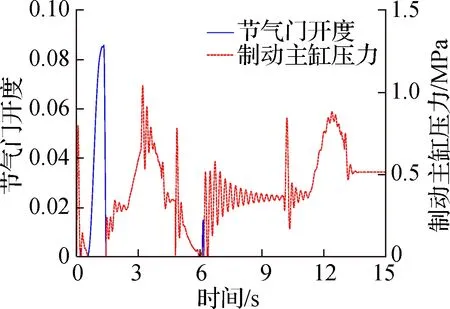
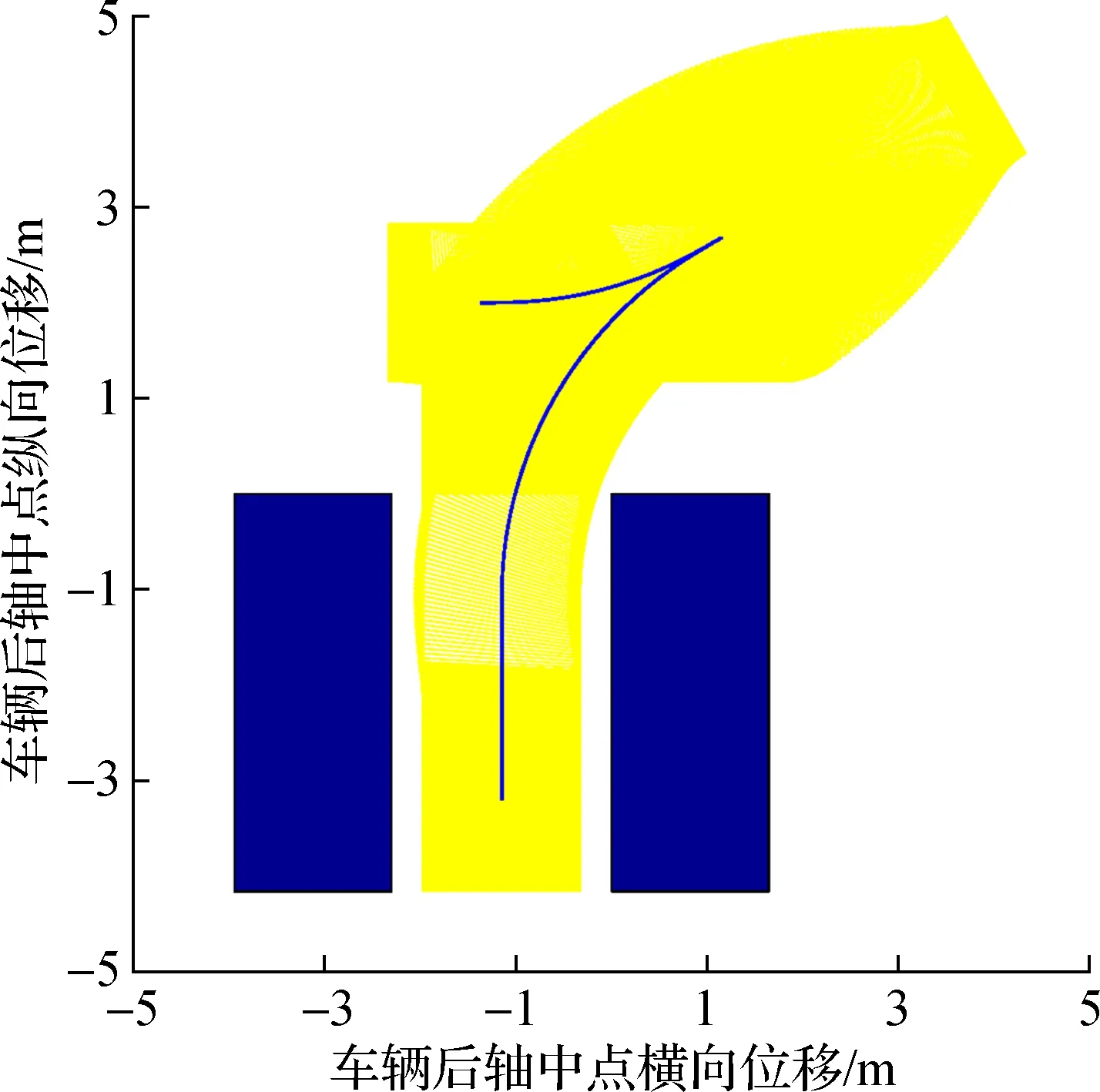
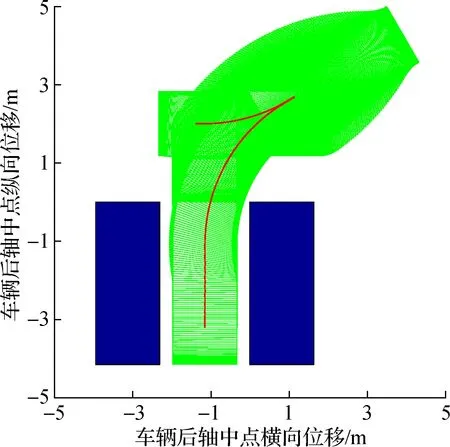
如图8所示，基于圆弧-直线方法规划的垂直泊车路径最短，但是在圆弧段与直线段的结合点处存在曲率突变，车辆必须执行原地转向才能跟踪基于圆弧-直线方法规划的垂直泊车路径；基于B样条曲线规划的垂直泊车路径与基于回旋曲线规划的垂直泊车路径的曲率均是连续变化的，但基于回旋曲线规划的垂直泊车路径更短，使得垂直泊车时间更短.如图7所示，基于2增益控制理论设计的非时间参考泊车路径跟踪2增益控制律可以使车辆精确地跟踪目标路径，并且在垂直泊车过程中无轮胎原地转向现象.如图9所示，基于PID控制方法设计的泊车速度跟踪控制律可以实现目标泊车速度的快速、精确、稳定的跟踪控制.如图10所示，蓝色区域为垂直泊车位两侧的障碍物，黄色区域为目标路径对应的车辆外轮廓包络，绿色区域为实际路径对应的车辆外轮廓包络，由车辆外轮廓包络和障碍物无相交可知：基于回旋曲线规划的垂直泊车轨迹可以安全、精确地引导车辆进入泊车位，基于2增益控制理论设计的非时间参考泊车路径跟踪2增益控制律与基于PID控制方法设计的泊车速度跟踪控制律可以在垂直泊车位宽度与车辆宽度之差大于0.655 m的前提下使车辆沿着规划的垂直泊车轨迹安全、舒适、精确地停放在垂直泊车位.

(a) 目标路径

(b) 泊车路径曲率沿泊车路径弧长变化

4 结论

1) 选择垂直泊车轨迹的弧长作为关联参考量，将垂直泊车轨迹规划问题解耦成路径规划问题和速度规划问题，降低了垂直泊车轨迹规划的难度.

(a) 车速

(b) 车速沿后轴中点横向位移变化

(c) 速度控制信号

(a) 目标路径的车辆外轮廓包络

(b) 实际路径的车辆外轮廓包络

针对垂直泊车路径规划问题，基于回旋曲线规划曲率连续的垂直泊车路径；针对垂直泊车速度规划问题，基于五次多项式曲线规划满足过程和边界约束条件的垂直泊车速度.

2) 将垂直泊车轨迹跟踪控制问题解耦成垂直泊车路径跟踪控制问题和垂直泊车速度跟踪控制问题.考虑垂直泊车轨迹跟踪控制系统的计算时延，采用预估模型预测下一采样时刻的车辆位姿和速度.针对垂直泊车路径跟踪控制问题，基于2增益控制理论设计非时间参考泊车路径跟踪2增益控制律.针对泊车速度跟踪控制问题，基于PID控制设计泊车速度跟踪控制律实现驱动系统和制动系统的平滑切换控制.

3) 结合硬件在环试验平台对所提出的垂直泊车轨迹规划与跟踪控制方法的可行性和有效性进行验证，结果表明：所提出的垂直泊车轨迹规划方法得到的泊车路径曲率是连续的，并且所提出的垂直泊车轨迹跟踪控制方法在泊车位宽度与车辆宽度之差大于0.655 m时可以安全、精确地引导车辆停放在泊车位.