热重分析解题模型构建

翁华怡

[摘   要]热重分析题常出现在高考化学试题中，其解题思路依托于学生的知识迁移和方法积累，综合性高。学生在解答过程中常出现畏难情绪。通过对热重曲线类型和物质受热失重方式的探究，帮助学生构建m-T热重曲线和ω-T热重曲线解题模型，在问题情境中提升学生的方法技能、思维品质和科学素养。

[关键词]热重分析;模型构建;科学素养

[中图分类号]    G633.8        [文献标识码]    A        [文章编号]    1674-6058（2020）29-0064-03

热重分析法是在一定条件下测量物质的质量随温度（或时间）变化的一种热分析方法，它是大学的知识，中学课本上没有热重分析法相关实验及仪器的介绍，但是解决热重分析题的方法却源于中学课本。热重分析题立足于学生的认知水平和知识技能，要求学生能够读取图像数据，并基于数据利用守恒思想分析化学变化，再通过定量计算进行推理，揭示反应过程，深受出题者的青睐。在2008-2019年江苏高考中出现过三次此类题型，分别是2010年、2014年的第18题和2019年的第20题。此类试题综合能力要求高，学生往往会有畏惧心理。因此，笔者认为有必要通过高考真题的探究，初步构建热重分析的一般解题模型，提升学生处理图像信息的能力和思维品质，培养学生的科学素养。

一、热重曲线类型

热重分析题通常会提供以质量（或质量比、质量百分率）为纵坐标，以温度为横坐标的热重曲线。根据图像纵坐标的差异，可将其分成m-T热重曲线和ω-T热重曲线两种类型。

二、失重方式模型构建

通过对高考真题和各地模拟题的研究可以发现：热重分析题均以图像为依托，要求学生推断不同温度下的组分，或以此来书写不同温度下的化学方程式。从图像角度对比，各试题图像有相似之处，质量（纵坐标）均随温度（横坐标）升高而呈现阶梯式下降，这表明在受热过程中，物质分步发生分解，在每个温度段区域都会形成较为稳定的物质。从物质角度对比，这一类物质往往是结晶水合物，在受热过程中容易先发生脱水，随后非金属元素形成的阴离子发生分解，若金属元素有变价，接下来常发生氧化还原反应，最终生成较为稳定的金属氧化物[1]。在变化过程中，固体中金属元素的部分是保持不变的，因此解题时应抓住金属元素守恒建立关系[2]。

三、解题模型构建

1. m-T热重曲线——三段式法

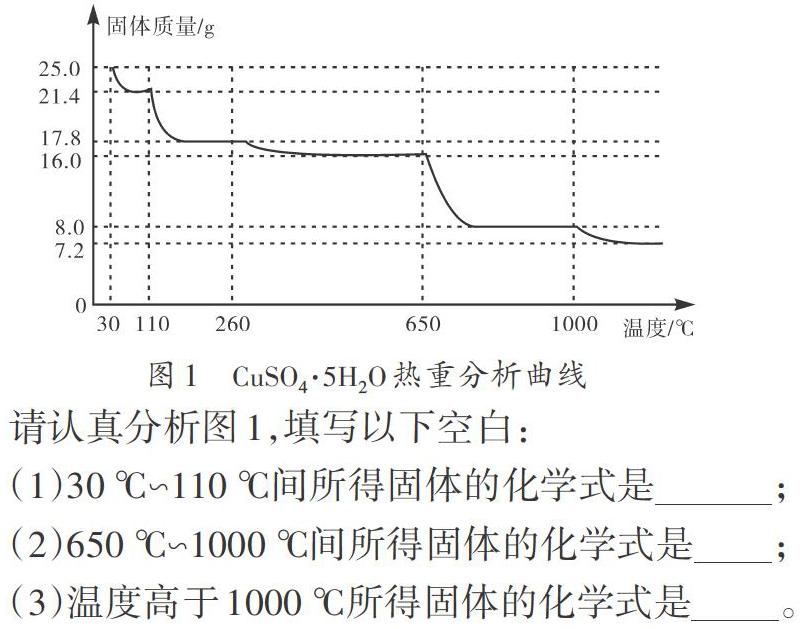
【例1】（2015年通州模拟，27）将25.0 g胆矾晶体放在坩埚中加热测定晶体中结晶水的含量，固体质量随温度的升高而变化的曲线如图1所示。

请认真分析图1，填写以下空白：

（1）30 ℃∽110 ℃间所得固体的化学式是_______________________;

（2）650 ℃∽1000 ℃间所得固体的化学式是____________________;

（3）温度高于1000 ℃所得固体的化学式是____________________。

解析：胆矾是学生熟悉的物质，我们可以参照失重方式模型找到2个特殊点：完全脱水的CuSO4和金属氧化物CuO。25.0 g CuSO4·5H2O的物质的量为0.1 mol，根据金属元素守恒，可以通过列三段式顺利计算出特殊点的质量。

对比题中数据，可知30 ℃、650 ℃、1000 ℃时固体分别为CuSO4·5H2O、CuSO4、CuO，因此在650 ℃∽1000 ℃加热阶段最终所得固体的化学式为CuO。由于110 ℃时固体质量介于16g与25 g之间，可以判定为部分脱水。根据Cu元素守恒，设110 ℃时固体的化学式为CuSO4·xH2O，根据铜元素守恒n（CuSO4·xH2O）=0.1 mol，m（CuSO4·xH2O）=21.4 g，M（CuSO4·xH2O）=160+18x=214 g/mol，解得x=3，所以110 ℃时固体的化学式为CuSO4·3H2O。

1000 ℃时固体已经是金属氧化物，考虑铜有变价，升高温度应该发生氧化还原反应，生成其他价态的金属氧化物。设高于1000 ℃固体的化学式为CuOx，根据铜元素守恒n（CuOx）=0.1 mol，m（CuOx）=7.2 g，M（CuOx）=64+18x=72 g/mol，解得x=0.5。在化学式中，各元素之比应写最简整数比，所以温度高于1000 ℃所得固体的化学式为Cu2O。

此类试题中的热重曲线的纵坐标较为简单，就是我们所要推断的组分质量。在解题时，可先找到特殊点（完全脱水产物、分解产物、金属氧化物）构建失重的过程，然后利用金属元素守恒，列三段式（m-M-n），随后对比特殊点数据和题目中所给具体数据，判断变化过程，最后就能通过精确计算，确定该温度区域下物质的化学式或书写相应的化学方程式。

2. ω-T热重曲线——巧设1 mol，转化为m-T热重曲线

在高考试题中，热重曲线中的纵坐标往往不是简单的质量，而是会发生变形，变成质量的比值。

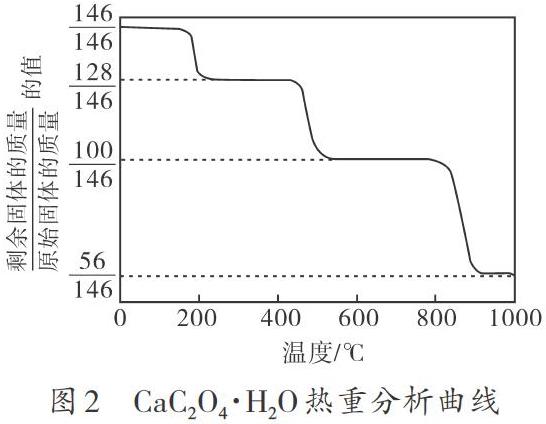
【例2】（2019年江苏，20）CaO可在较高温度下捕集CO2，在更高温度下将捕集的CO2释放利用。CaC2O4·H2O热分解可制备CaO，CaC2O4·H2O加热升温过程中固体的质量变化如图2所示。写出400 ℃∽600 ℃范围内分解反应的化学方程式：_________________________。

解析：观察图像可以发现纵坐标为比值形式，而分母均为146，恰好与CaC2O4·H2O的摩尔质量数值相等，因此可以假设CaC2O4·H2O为1 mol，即原始固体质量为146 g。若纵坐标统一乘以146，就可以将比值转化为剩余固体的质量，如表1所示。此时就将ω-T热重曲线转化为m-T热重曲线。

纵坐标除了变形为质量的比值，还可为固体残留率（百分数）。

解析：观察图像可以发现纵坐标为百分数，结合题意，固体残留率即剩余固体的质量分数。此时纵坐标的含义与例2接近，只要知道原固體的质量就可以进行相同的转化。为了方便计算，我们依旧设原固体为1 mol，转化数据如表2所示。

解得x=1.5，y=1.33，即290 ℃、500 ℃时所得固体的化学式为Co2O3、Co3O4，因此1000 ℃时，剩余固体成分为CoO，在350 ℃∽400 ℃范围内，剩余固体成分为Co2O3。

除此之外，纵坐标还可转化为失重率。

已知：[失重%=加热减少的质量原晶体样品的总质量×100%]。

解析：此时纵坐标的含义为减少的固体的质量分数。剩余固体质量=原固体总质量×（1-失重%），同样，可以设硫酸铝晶体为1 mol进行数据转化，如表3所示。

通过以上例题可以发现，无论纵坐标怎么改变，首先需要分析图像，理解纵坐标表达的意义;其次，巧设“1 mol”进行还原，将百分数转化为剩余固体质量，从而将ω-T热重曲线转化为m-T热重曲线来解题。

教学实践表明，在试题讲解过程中，引导学生结合图形[3]，抓住关键信息，利用已有知识进行分析推理，有利于提高学生思维的严密性和迁移知识的能力。同时在解题的过程中构建模型，更能消除学生的畏惧心理，引导学生体验探究过程，激发学生的求知欲，提升学生的科学素养。

[   参   考   文   献   ]

[1]  韩江涛，杨云. 中学化学热重曲线类试题文献分析及建议[J].化学教学，2016（7）：82-86.

[2]  房寿高. 热重分析类化学计算题的解题方法[J].新高考（高三理化生），2014 （10）：38-41.

[3]  高晓莹，吴春峰. 基于作图和识图角度评析热重分析图形[J].中学化学教学参考，2014 （5）：50-51.

（责任编辑 罗   艳）