基于乘客群体出行时间间隔的标度律研究

李飞羽，翁小雄，姚树申

(华南理工大学 土木与交通学院，广东 广州 510640)

随着城市公交IC卡的普及，研究者能更加客观地从IC卡刷卡数据中挖掘出乘客的出行特性，例如通勤识别[1]、乘客上车耗时[2]等，从而为交通管理部门制定相关政策提供了理论支撑。以全样本IC卡刷卡数据为基础，对乘客群体出行时间间隔的标度律进行研究，可以为交通管理部门预测乘客出行时间提供理论支撑，同时也可以拓展人类行为动力学研究的方向。

Barabasi等[3-4]提出的简化行为时间间隔分布普遍具有非泊松分布现象和人类行为时间特性，同时具有短时爆发与长时静默并存的特点，这一研究开辟了人类行为动力学的新领域。Vázquez[5]提出了人类行为动力学中的普适幂指数为-1或-1.5，但是否存在其他的普适类，仍待学者去研究。目前国内外对人类行为时间间隔的研究主要分为两种类型：第一种是对人类行为时间间隔的分布进行实证研究。如Zhao等[6]和徐宇[7]证实了用户在社交平台上发布评论转发等行为的时间间隔是服从幂律分布的；樊超等[8]实证了用户在线学习的时间间隔服从幂律分布；姜春昕[9]实证了人们参加线下活动的时间间隔分布存在胖尾现象。李瑾颉等[10]对人类行为时间间隔的实证研究进行了综述，并提出了社交网络信息传播与用户的时间特征是互相作用的。该类研究证实人类行为时间间隔服从幂律分布，但没有对产生幂律分布的机制进行分析。第二种是利用理论解释人类行为时间间隔分布特征。如徐达[11]利用活动驱动理论解释了社交网络的用户行为时间间隔服从幂律分布的原因；张杰斌等[12]利用排队理论解释了人类行为时间间隔服从幂律与指数分布产生的机制；崔晓萌[13]利用改进的排队理论研究发现了居民群体出行时间间隔服从幂律分布；沈洪洲等[14]和Yang等[15]研究发现用户在网络上的购买行为的时间间隔服从幂律分布，并基于兴趣自适应理论进行了解释；Yan等[16]和张艳丰[17]利用阵发性理论解释了网络用户行为时间间隔的胖尾现象。Li等[18]利用兴趣模型解析了不同类型的人群使用新浪微博的时间间隔差异性。Zhou等[19]对由建筑工人不规范的操作导致事故发生的时间间隔进行了研究，发现了时间间隔呈现出的强爆发性与弱记忆性，并基于幂指数提出一种新的安全绩效指标。这类研究用数学模型合理解释了人类行为时间间隔服从幂律分布的现象，为研究人类行为时间间隔产生幂律分布的机制提供了新的视角，但对如何形成幂律分布的内在机制分析得不够全面。

综上所述，国内外大多数研究对人类行为时间间隔标度律产生的机制分析得不够全面，且鲜有学者对公交乘客出行时间间隔标度律进行研究。

乘客出行有别于人们在网络上的行为，具有高度的复杂性，受出行目的和工作节律等多方面主客观因素影响。本文从乘客公交IC卡刷卡数据出发，利用粒子群算法对乘客群体出行时间间隔的概率进行拟合， 并利用阵发性理论、乘客出行规律以及出行目的来解释乘客群体出行时间间隔的概率拟合结果，在此基础上宏观预测乘客出行时间，从而为公交管理部门制定相关政策提供理论依据。

1 出行时间间隔的均匀性与标度律模型分析

行为时间间隔是人类行为动力学研究的核心统计量。本节从乘客出行时间间隔出发，分析乘客出行时间间隔的均匀性与时间间隔的标度律模型。

1.1 出行时间间隔

出行时间间隔是某位乘客后一次刷卡时间与前一次刷卡时间之差，其定义为：

ΔTj=Tj+1-Tj,j=1,2,3…

(1)

式中Tj表示第j次刷卡时间，ΔTj表示第j+1次刷卡时间与第j次刷卡时间之差。按照式(1)将每个乘客出行时间间隔统计出来，作为乘客群体出行时间间隔的数据集。

1.2 出行时间间隔均匀性的分析

1.2.1 出行时间信息熵

香农熵(Shannon entropy)是用来度量信息不确定性的物理量，其定义为：

(2)

式中i表示随机事件，pi表示随机事件的概率。当H(x)越大，表示事件发生越随机。

乘客出行时间信息熵[20]定义为：

(3)

式中的时间段按小时来划分，根据公交车运营时间可划分为19个时间段。pi(j)表示乘客i的出行时间在j时间段的概率。乘客出行时间信息熵越大，则出行时间越随机且时间间隔越不均匀。

1.2.2 出行时间间隔的阵发性

乘客出行并非类似泊松过程，而是在某一时刻密集发生，然后较长的时间不发生。这种过程称为出行的阵发过程，Bgoh K I等[21]提出了阵发性的定义：

(4)

式中B的取值范围为-1到1，其中στ,mτ分别代表时间间隔的标准差和平均值。阵发性越接近-1，表示乘客出行间隔时间越接近周期信号。时间间隔分布为泊松分布时，阵发性为0。当阵发性大于0时，时间间隔分布会呈现出胖尾现象。阵发性越接近1，则表示时间间隔分布的胖尾现象越明显。

1.3 出行时间间隔的标度律

标度律是指物理量所具有的某种普适性，通过出行时间间隔的标度律研究可以挖掘出乘客出行时间间隔的集中范围以及标度律形成的动力机制。在人类行为动力学的研究中，常见的标度律有两种形式：指数形式与幂律形式。

1.3.1 指数形式

泊松过程可以很好地解释经典的随机过程，常用于量化人类行为活动。在泊松过程中，两个随机事件时间间隔的概率密度函数具有指数形式：

PE=αexp (βx)。

(5)

1.3.2 幂律形式

Barabasi等[1-2]基于任务队列理论模型对人类行为实证发现，人类行为时间间隔的概率密度函数具有幂律形式：

Pp=α(x)β。

(6)

具有幂律形式的分布会呈现胖尾现象，而具有指数形式的分布在尾部是均匀下降的。大部分人类行为时间间隔的分布都近似为幂律分布，但是乘客出行时间间隔的标度律鲜有研究且尚无统一标准，因此本文假设其可用幂律形式或者指数形式来近似拟合。

2 粒子群算法模型

粒子群算法[22]是一种基于迭代优化的算法，具有很强的寻优能力。本节通过介绍粒子群算法基本原理和参数设置，从而构建出标度律拟合的步骤。

2.1 基本的PSO算法

一个M维空间里面有n个粒子组成的群体：X={x1,x2,…,xn}，该群体粒子以一定的速度在运动，每个粒子都有自己的位置与速度。第i个粒子位置为xi={xi1,xi2,…,xiM}，速度为vi={vi1,vi2,…,viM}。在寻优的过程中，第i个粒子记录迄今为止搜索到的个体最优位置pi={pi1,pi2,…,piM}，而整个粒子群记录迄今为止搜索到的全局最优位置Gi={p1,p2,…,pn}。粒子通过个体最优位置和全局最优位置更新其速度vi和其位置xi，对应的公式如下：

vi=ωvi+c1r(pi-xi)+c2r(Gg-xi)，

(7)

xi=xi+vi，

(8)

式中，c1，c2都是学习因子，可以调节粒子个体与全局最优方向，使得迭代的收敛速度加快。r是(0,1)之间的随机数字，可以确保粒子具有全局最优能力和算法具有随机性。为了防止粒子盲目寻优，将位置和速度的值限制在合理的范围内:xi∈[-xm,xm]，xm表示位置的最大值；vi∈[-vm,vm]，vm表示速度的最大值。

2.2 参数的设置

2.2.1 学习因子的调整

学习因子的调整可分为异步时变和同步时变。同步时变是指学习因子在调整过程中进行同步线性的变化，异步时变是指学习因子在调整过程中进行异步线性的变化。该方法的优点在于使得粒子群算法在初始阶段具有良好的全局优化能力，在寻优的后期使粒子可以收敛到最优解。这些调整发生的频率将随着迭代次数不断增加。同时随着迭代次数增加，c1值不断减小，c2值不断增加。可以设置以下调整方式：

(9)

(10)

其中c1E表示c1的初始值；c1S表示c1的最终值；c2E表示c2的初始值；c2S表示c2的最终值；R表示当前迭代次数；Rmax表示最大迭代次数。

2.2.2 惯性权值的调整

在调整学习因子的同时，对惯性权值也进行调整。本文使用线性调整方式来调整惯性权值。在ω的值域内，调整公式为：

(11)

式中，ω表示第R次迭代的惯性权值；ωmax表示惯性权值的最大值；ωmin表示惯性权值的最小值；Rmax表示最大的迭代次数。通过惯性权值公式调整后，粒子具有较优的寻优能力。

2.3 适应度的设置

本文分别使用式(4)与式(5)作为粒子群算法拟合的目标函数f(x)，最优个体适应的公式为：

(12)

式中，y(x)表示实际值；f(x)表示理论值，适应度ffitness(x)越小则拟合效果越好。

2.4 PSO的算法步骤

步骤1：初始化粒子的位置和速度；设置粒子位置和速度的范围；设置粒子群的规模、迭代次数和学习因子。

步骤2：计算每个粒子适应度值。

步骤3：将当前粒子适应度值与其经历过的个体最优解的适应度值作比较。如果较小，则把当前粒子位置作为个体最优解，否则个体最优解不变。

步骤4：将当前粒子适应度值与其经历过的全局最优解的适应度值作比较。如果较小，则把当前粒子位置作为全局最优解，否则全局最优解不变。

步骤5：根据步骤3和4得到的个体最优解与全局最优解，对速度和位置进行调整和优化，同时学习因子也线性变化。

步骤6：如果到了预定的运行精度或迭代次数，则停止迭代并返回解析式相应的参数，否则回到步骤2继续执行。

3 案例分析

本文以珠海市2015年3月1日到5月31日的乘客公交IC卡刷卡数据为案例，随机选取了22 022个乘客4 383 897条刷卡记录进行研究。采用粒子群算法对乘客群体出行时间间隔的概率分布进行拟合并用校正决定系数Rsquare进行判断。

3.1 出行时间间隔概率的拟合

3.1.1 粒子群参数的设置

将式(4)、(5)作为粒子群算法拟合的目标函数。设置初始种群为100，最大迭代次数为100，粒子学习因子为1.494 45，惯性权值为0.5～1，速度为-1～1。

3.1.2 拟合结果与分析

乘客群体出行时间间隔标度律的拟合方法：先将所有乘客的出行时间间隔按照小时来分段，时间间隔在1 h内的当作1 h处理，统计每个时间间隔的概率值，然后用粒子群算法拟合概率的分布。在双对数坐标下，群体出行时间间隔的概率分布如图1所示。从整体来看，概率分布的形状有平缓的头部和明显的胖尾，中间部分非常陡峭。以幂律形式的标度律作为目标函数，利用粒子群算法对中间部分与尾部部分的概率进行拟合，拟合得到直线如图1所示。拟合得到最优个体适应度值为2.982，如图2所示。拟合得到的幂指数为-2.599，且计算得到的Rsquare为94.8%，因此可判断群体出行时间间隔在中部和尾部是服从幂律分布的。从中间部分与尾部中可得：乘客出行时间间隔较大(大于14 h)的概率较小，此部分的概率占整体的比例仅有21.8%，表明较大的时间间隔并非乘客出行时间间隔的主要集中范围。

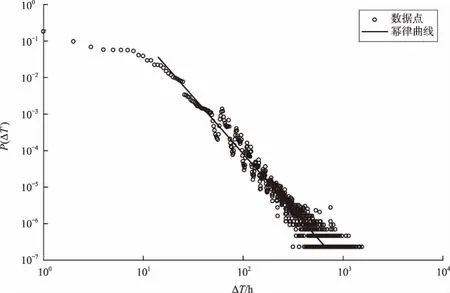
图1 群体出行时间间隔的概率分布Fig.1 Chart of distribution of time intervals probability of passengers’ groups

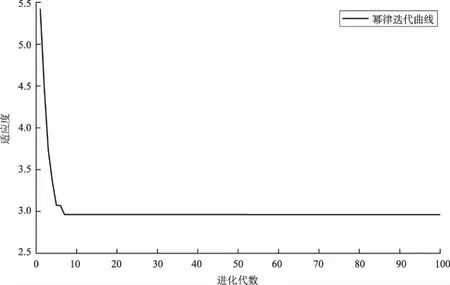
图2 出行时间间隔大于14 h的迭代曲线Fig.2 Iterative curve with time interval greater than 14 h

平缓的头部范围为1～14 h，其比例占整体的78.2%。因此平缓的头部代表了乘客出行时间间隔的主要集中范围，是预测乘客出行时间的重要依据。头部的时间间隔是否均匀从图1中无法确定，因此分别使用指数曲线和幂律曲线来拟合概率分布的头部，拟合效果如图3和图4所示。由图3与图4可得幂律拟合迭代的最优个体适应度值更小，由此可得幂律曲线拟合群体的头部更加合适。由迭代结果得到幂律曲线对应的幂指数为-0.706，计算得到的Rsquare为0.961 2，而指数曲线拟合的Rsquare为0.789 3。由上述分析可得：乘客群体出行时间间隔服从幂律分布，但存在着幂律的分层。头部对应的幂指数为-0.706，而中部和尾部对应的幂指数为-2.599，表现出头部下降缓慢而中间部分和尾部下降较快。

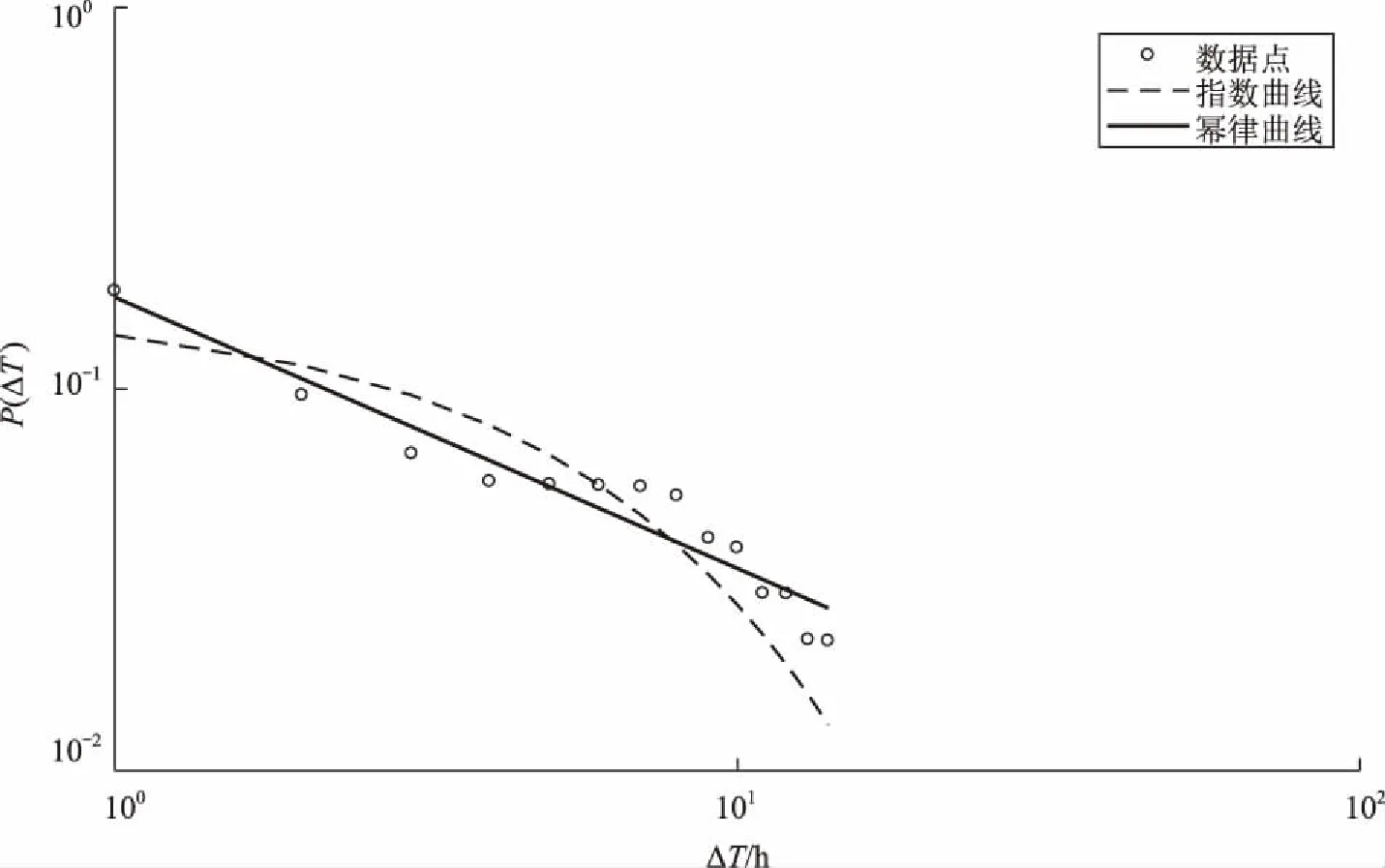
图3 时间间隔在14 h范围的概率分布Fig.3 Chart of distribution of the probability of the time interval in the 14 h range

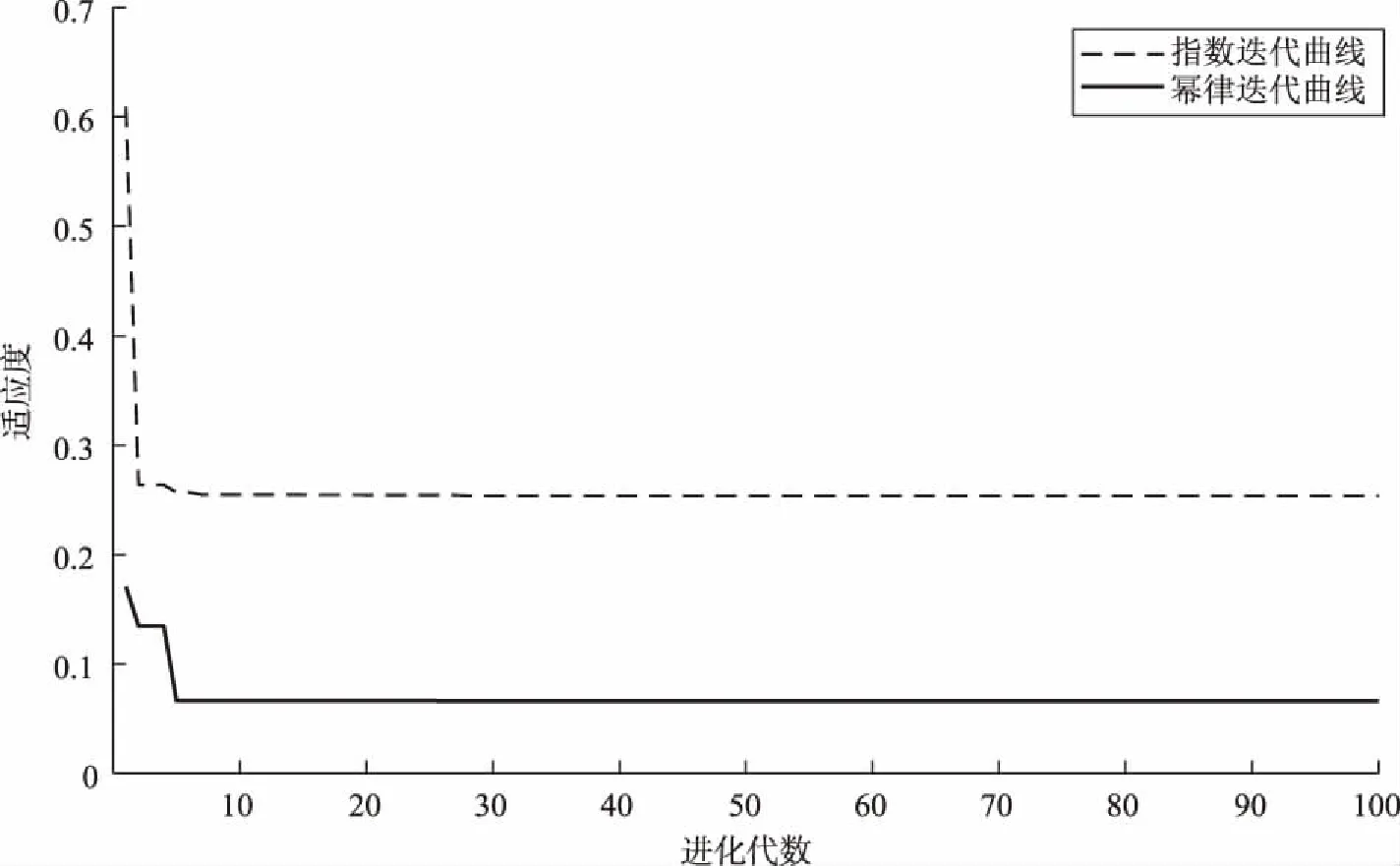
图4 时间间隔在14 h范围的迭代曲线Fig.4 Iterative curve with time interval in the 14 h range

3.2 形成机制分析

分析群体时间间隔服从幂律分布的机制，对研究乘客出行背后蕴含的动力具有重要意义。

3.2.1 阵发性分析

对于人类行为时间间隔分布服从幂律分布这一现象，许多学者用阵发性对其进行了定量分析。由上文分析可得大部分乘客出行时间间隔主要集中在14 h范围内。由于众多的个体时间间隔的累加，14 h范围内的概率下降速度较为缓慢且对应幂指数的绝对值较小。时间间隔大于14 h的概率占整体21.8%，在此范围内个体时间间隔累加较少，从而对应的概率下降速度较快且对应的幂指数绝对值较大。由上述分析可得群体的时间间隔范围较大，因此时间间隔标准差较大，而大部分时间间隔聚集在小范围内，因此群体的时间间隔平均值较小。可算得时间间隔的平均值为40.36 h，标准差值为63.41。通过式(3)可求得阵发性为0.222，因此群体时间间隔的分布呈现胖尾现象。

3.2.2 出行时间规律分析

出行规律反映了乘客出行的时间间隔是否均匀。本节从乘客个体出发，计算每个乘客出行时间信息熵。如表1和图5所示，大部分乘客出行时间信息熵在3.5附近，表示大部分乘客出行时间较随机。出行时间规律较强的乘客，时间间隔较为均匀；出行时间较随机的乘客，出行时间间隔较为不均匀。较均匀的时间间隔与众多较不均匀的间隔汇聚到乘客群体层面，使得时间间隔不均匀性更强，从而表现出非常明显的非泊松分布现象。

表1 乘客出行时间信息熵的统计

3.2.3 出行目的分析

出行目的是乘客出行属性的重要内容，也是理解乘客出行动力的基础。通勤类乘客的出行具有短时间的密集发生和长时间的静默并存的特征。产生这种特征的主要原因为：①由于公交车运营时间和生理作息的影响，此类乘客集中在早高峰出行；②由于工作节律的影响，此类乘客在晚高峰密集出行，因此通勤类乘客出行时间间隔主要集中在头部。而基于生活目的出行的乘客，其出行时间异质性更强，即出行时间间隔的分布范围大且不均匀，但主要以时间间隔较小的居多。个体的时间间隔聚集到群体层面时，时间间隔较小范围的概率大于时间间隔较大范围的概率。

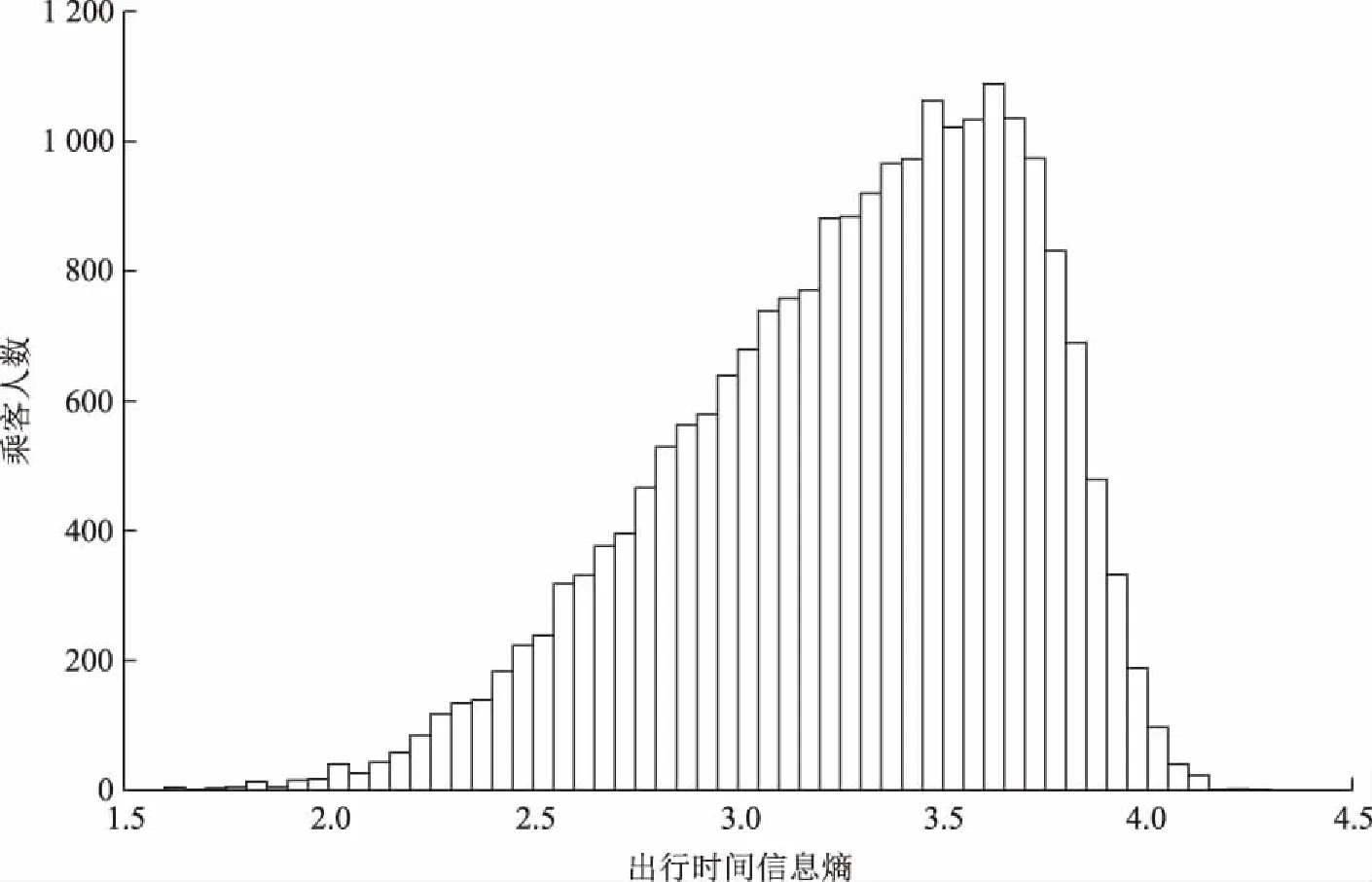
图5 乘客出行时间信息熵的分布Fig.5 Chart of distribution of information entropy of passengers’ travel time

4 结论

本文通过粒子群算法拟合发现了乘客群体时间间隔分布呈现多尺度特征：小于14 h和大于14 h两个范围分别服从指数为-0.706与-2.599的幂律分布，并非大部分研究所提到的人类行为时间间隔分布具有统一的幂指数，且与Vázquez所总结的两大类幂指数不同。78.2%的出行时间间隔聚集在14 h内，此范围的概率较大且下降速度较缓慢，因此对应的幂指数较大；21.8%的出行时间间隔大于14 h，此范围的概率较小且下降的速度较快，因此对应的幂指数较小。

基于阵发性得出以下结论：群体时间间隔的平均值为40.36 h，标准差为63.4，标准差大于均值使得分布呈现出胖尾的现象。

此外，基于乘客的出行规律以及出行目的得出以下结论：群体在众多个体的特性聚合下往往会掩盖个体的行为特性的不同。不同乘客的出行规律和出行目的等因素使得群体出行时间间隔变得更加不均匀，因此对应的概率分布形状有平缓的头部和明显的胖尾。通过分析概率分布的头部，可以得到乘客的出行时间间隔主要集中在14 h内。这个范围占据了群体时间间隔的78.2%，因此可以通过出行时间间隔的集中范围，宏观上预测乘客出行时间。但本文工作仅涉及乘客群体的时间间隔分布，没有深入到乘客个体层面。因此后续的研究工作可以深入到个体层面，在充分理解社会复杂系统基础上，进一步探索幂律分布的产生机制。