基于时间序列线性大数据分析的电力系统潮流计算方法

，，，，

(1.国网河南省电力公司电力科学研究院客户服务中心，河南 郑州 450000； 2.国网河南省电力公司，河南 郑州 450000)

0 引言

在处于使用数字计算机对电力系统潮流问题求解的开始阶段时，人们对其要求较低，数字计算机的内存量也比较小。而现如今，电力系统规模不断扩大，已经形成了十分复杂的网络结构，人们对其要求也逐渐升高，原有的电力系统潮流计算方法，已经难以达到电力系统的大规模数据分析以及控制要求[1]。

对于一些病态系统，应用非线性潮流计算方法往往会造成计算过程的振荡或者不收敛。采用逐次线性化的方法，使计算速度以及所发的收敛性得到进一步的提高[2]。所设计方法的创新点是：分析电力系统调频特征；建立电力系统潮流模型。

根据电力系统的特点，抓住主要矛盾，采用时间序列分析方法，将同一统计指标的数值按其发生的时间先后顺序排列，在数据中挖掘出其根据时间变化的相关规律，并对之后的数据作出合理估计[3-4]。从而根据估计结果，分析电力系统的运行情况，得出电力系统潮流计算结果，使电力系统的稳定计算以及故障分析工作能够顺利完成。

1 基于时间序列线性大数据分析的电力系统潮流计算

将时间序列线性大数据分析，应用到电力系统的潮流计算当中，需要分析系统调频的相关特性[5]，并在其基础上建立电力系统潮流模型，该具体流程如图1所示。

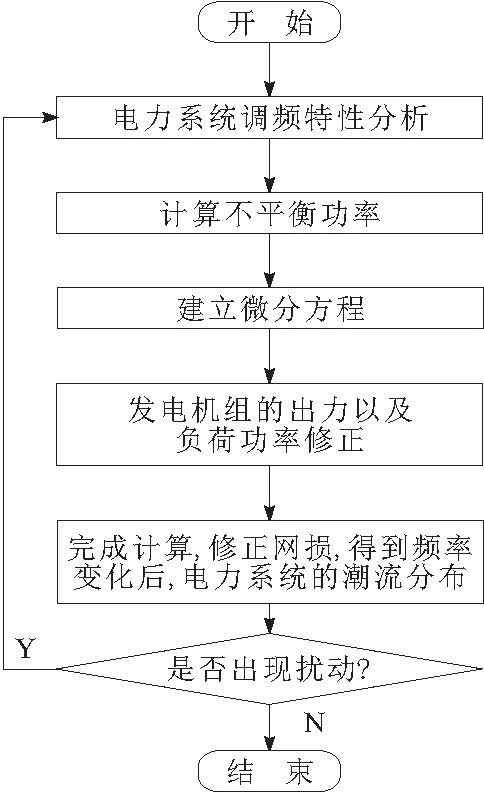
图1 电力系统潮流计算流程

由图1可知，若电力系统的潮流分布出现扰动，需重新分析电力系统调频特性，计算不平衡功率。根据对电力系统调频特性的分析结果，保证网络功率平衡，得到其网络损耗，建立电力系统潮流模型，完成计算。

1.1 基于时间序列线性大数据的电力系统调频特性分析

在完成电力系统潮流计算流程的基础上，分析基于时间序列线性大数据的电力系统调频特征。电力系统的频率是对电能质量的重要衡量指标，其标准频率的规定值为50 Hz，偏差一般在0.2 Hz左右[6]。当发电机的输出功率，受到系统频率变化的影响，而随之产生变化时，通过发电机组调速器，使其原动机的输入得到改变，从而改变发电机组的出力，将电力系统的有功功率供给与需求量之间保持平衡[7-8]，保证其频率维持在正常范围内，其具体情况如图2所示。

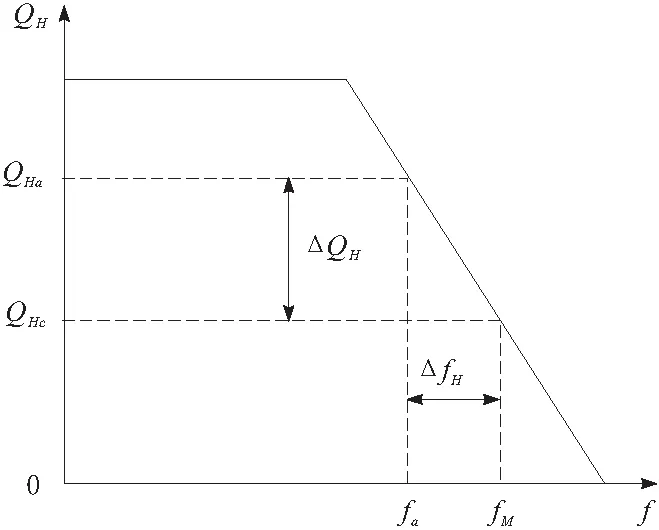
图2 发电机的频率特性

由图2可知，当发电机组在额定频率fM下运行时，其有功功率为QHc。若电力系统的频率下降至fa，则利用调速器作用，将发电机组的出力改变至QHa，通过计算可以得出其特性曲线的斜率为

(1)

ΔfH为发电机组的单位调节功率，即发电的频率系数，发电机组的频率与有功功率变化方向是相反的，其输出功率将会随频率的降低而增加，反之相同[9]；ΔQH表示频率偏差为ΔfH时，发电机组的输出有功增量。

将线路损耗的部分简化当做负荷的一部分，并将电路系统中的发电机组与负荷简化为各有且仅有一个，则系统的调频情况如图3所示。

由图3可知，调频完成后的频率变化量需满足：

Δf=fB-fM<0

(2)

fB为电力系统频率的延迟算子；fM为电力系统频率的梯度算子。

若电力系统的实际变化量是负值，则其负荷功率的实际变化量为

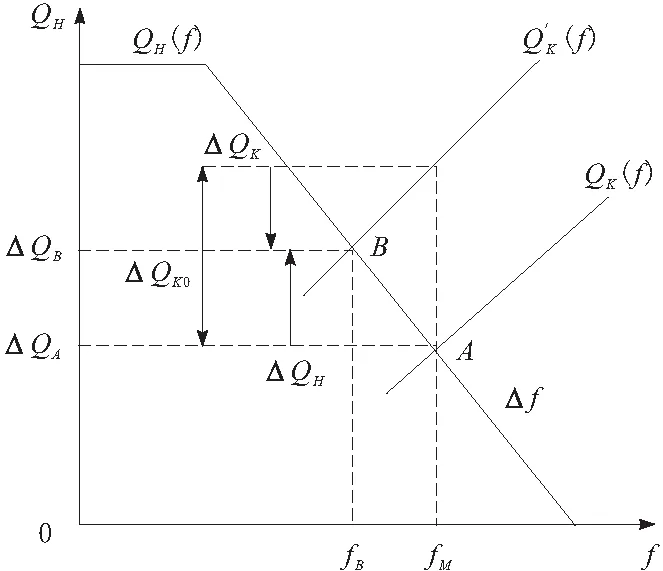
图3 电力系统调频示意

(3)

式(3)中变量定义如图2中所标示。当电力系统在完成调频达到平衡点B时，与平衡点A对比，能够发现系统的实际负荷功率与发电机功率变化量相等，则通过图2与式(3)可以得到

ΔQK0=ΔQH-ΔQK=-GsΔf

(4)

Gs为电力系统功率，即系统负荷产生变化时，在调速器作用下，电力系统的频率变化程度[10-11]。通过上述计算能够得知，系统受负荷扰动影响所产生的频率变化随Gs数值的增大而减小，即系统频率越稳定。

至此完成在时间序列线性大数据基础上，电力系统调频特性分析，并根据分析结果，建立电力系统潮流模型。

1.2 电力系统潮流模型建立

在潮流计算中，电力系统的各部分处于同一频率，但受到发电机的启动停止或是其输出功率产生变化的影响时，系统将会产生不平衡功率[12-13]，为此利用时间序列线性大数据分析算法，计算其相应数值为

Qacc=∑QHi-∑QKi-Qloss

(5)

QHi为处于i节点时的有功功率；QKi为处于i节点时的负荷有功功率；Qloss为电力系统的有功损耗。

将发电机组的参与一次调频时的迟滞时间忽略不计，结合调速器的相关特性以及负荷特性，利用转子运动方程，得到电力系统功率——频率潮流表达式为

(6)

YH∑为将电力系统中的全部同步发电机组，等值为1台机器的惯性时间常数；GK∑为电力系统的综合负荷频率特性系数；GH∑为将电力系统中的全部同步发电机组，等值为1台机器，对电力系统的单位调节功率。式(6)中各参数的计算过程如下所示。

惯性时间常数计算方法为

(7)

YHi为对应节点i上同步发电机组的惯性时间常数；DHi为对应节点i上同步发电机组的额定容量；DN为电力系统的基准容量；g1为系统中全部常规同步发电机组个数。

电力系统的全部同步发电机组，等值为1台机器，对电力系统的单位调节功率计算方法为

(8)

GHi为对应节点i上发电机组的静态频率系数；QHMi为对应节点i上发电机组的额定功率。

电力系统的综合负荷频率特性系数计算方法为

(9)

g2为系统中全部负荷点的个数；GKi表示对应节点i上的负荷静态频率系数。其他变量定义与上式相同。

经过上述各参数计算，由此完成基于时间序列线性大数据分析的电力系统潮流计算。由上述计算能够得知，在电力系统的潮流计算中，发电机的出力以及负荷功率数值都是不固定的，并在计算过程中，跟随不平衡功率的变化而产生变动。

利用时间序列线性分析算法，将不平衡功率分散至电力系统中，通过具有调节能力的发电机组以及负荷承担[14-15]。至此完成基于时间序列线性大数据分析的电力系统潮流模型建立。

2 仿真实验

考虑到电力系统中，发电机出力随机变化、负荷波动等功率随机扰动因素对电力系统频率的影响，设计上述方法，完成基于时间序列线性大数据分析的电力系统潮流计算方法，为验证该方法的有效性，设计仿真实验。

2.1 实验准备

在不考虑风电场地形等因素的影响下，利用风电机组进行实验操作，将PQ视为节点，其电力系统的原理如图4所示。

为保证该实验的严谨性及公正性，随机选取某电力系统节点，采用PSASP电力系统分析综合程序，输入相同的初始数据，分别模拟原有方法以及所设计方法的计算准确度，对比所得结果，其具体操作过程如图5所示。

图4 电力系统的原理电路

图5 操作流程

由图5可知，在精度与迭代效率的计算后可选择初始矢量，以此完成计算。根据上述操作流程完成电力系统潮流计算过程模拟，分析其所得结果，验证所设计方法的计算准确度。

2.2 实验对比分析

利用PSASP电力系统分析综合程序设定相关操作数据，计算得到其概率分布情况如图6所示。

图6 概率分布示意

由图6可知，其期望值为0.984 Hz，方差为0.013 Hz，表1为计算得出的节点电压幅值标准差对比结果。

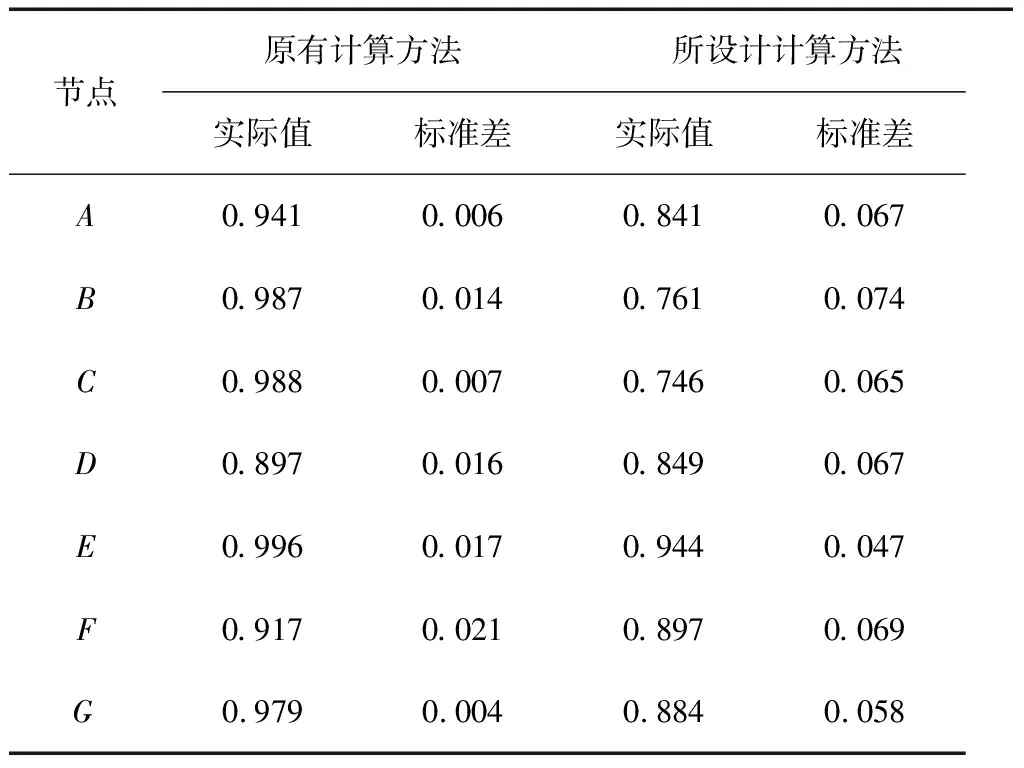
表1 实验对比结果

由表1的结果数值能够得知，与原有方法相比较而言，所提出的方法计算准确程度更高。该电力系统潮流计算方法能够更加全面地考虑到随机扰动对系统频率所产生的影响因素，所设计方法得到的标准差明显小于原有方法，实际结果与期望值差距较小，证明该方法有效。

3 结束语

电力系统规模不断壮大，复杂的网络结构日趋完善，但原有的电力系统潮流计算方法已经不能满足此趋势，难以达到电力系统大规模数据分析的要求，为了解决上述提到的不足之处且优化电力系统的运行，由全部可行的潮流解中，挑选出满足一定指标要求的最佳方案，同时考虑电力网络的经济性和安全性。将时间序列线性大数据分析应用于电力系统的潮流计算方法当中，根据数据量与量之间按比例、成直线的关系，在电网规划的阶段中，通过潮流计算，完成电源容量及接入点，以及网架的规划。并根据计算结果，预想事故、设备退出运行对静态安全的影响分析，从而对预想的运行方式合理调整。为此需要保证潮流计算的精准，为电网的正常运行夯实基础。对系统调频的相关特性加以分析，根据其分析结果，建立电力系统潮流模型，完成方法设计。并通过仿真实验，证实该方法的有效性，为电力企业的相关工作及研究提供一定的理论指导。