海啸波对斜坡堤爬高试验研究
2020-01-15刘鑫吕迎雪李江峰张文忠丁广佳
刘鑫 ,吕迎雪 ,李江峰 ,张文忠 ,丁广佳
(1.中广核工程有限公司核电安全监控技术与装备国家重点实验室,深圳中广核工程设计有限公司,广东 深圳 518172;2.中交天津港湾工程研究院有限公司,天津 300222;3.中国交建海岸工程水动力重点实验室,天津 300222)
0 引言
2011年3月福岛第一核电站因受海啸侵袭发生事故后,国内核电厂进行了安全排查,对地震海啸等外部灾害进行了复核评估。由于我国沿海自然条件特点,以往国内对海啸的关注和研究相对较少,对海啸与构筑物作用方面缺少资料和工程技术经验。海啸波本质上是一种长波,具有明显的单一波峰形状,其波高及水深相对于波长来说均为小值,属于浅水长波。由于孤立波的波形与传播特性与海啸波类似,并且其波形函数简单易于数学解析,因此常以孤立波模拟海啸传播变形。同时海啸模型试验研究也随着造波系统可以准确模拟孤立波而得到了快速发展,由孤立波传播的变形试验为相关的数值模拟提供了重要的基础资料。
国外Hall&Watts[1]最早在实验室研究了孤立波沿缓坡传播后波浪的变形,Synolakis(1987年)[2]根据1颐20的斜坡试验结果得出孤立波最大爬坡高度的估算公式。Hsiao等(2008)[3]根据试验结果利用最小二乘法归纳出斜坡在一定倾角范围内破碎孤立波爬高,国内张文忠[4]通过物理模型试验提出了两种坡率的海啸波爬坡公式。“311地震”发生以后,日本的研究学者针对防海啸防波堤护面及基床的稳定性开展了一系列研究工作,Mikami等(2012)[5]首先对海啸中不同结构形式的防波堤破坏情况进行了实地调查。Esteban等(2012a)[6]提出了护面块体抗海啸波的设计参数计算公式,但是这个公式只是通过日本东北部的2个港口的分析得出,因此公式应用有局限性。Hanzawa等(2012)[7]以及 Kato等(2012)[8]也提出了计算海啸波作用下的护面块体的设计公式,这个公式里考虑了流速及越浪的影响,但其中参数获取较困难,较难应用。
根据工程上的需要,针对两种坡度、不同护面块体的斜坡式防波堤结构断面进行了海啸波作用物理模型试验,得到了不同水深波高工况下海啸波沿斜坡堤的爬高数据,并将试验结果与前人的经验公式进行了对比,加入了糙渗系数,提出了改进的海啸波沿斜坡堤爬高的经验公式,为以后工程上的实际应用提供参考依据。
1 物理模型试验概况
1.1 试验设备
海啸波对斜坡堤断面物理模型试验是在中交天津港湾工程研究院有限公司水工研究所的无反射造波机试验水槽中进行。水槽的长度、宽度、高度分别为68.0 m、1.0 m和1.6 m。造波机系统由造波板、伺服电机、造波机控制器、计算机控制系统和数据采集、分析系统组成。该造波机系统是2005年6月从日本三井造船株式会社引进,是国内成功引进的第一座无反射造波机成套设备。该系统可以在0.5耀4.5 s的周期范围内模拟不同谱型的不规则波和特定形式的非线性波,并可以在水槽中生成孤立波模拟海啸。
1.2 试验布置及观测方法
无反射造波水槽一端安有造波机,尾端铺设大块石进行消波。本次试验在水槽中为测量海啸波在斜坡堤上的爬高变形过程及最大爬坡高度,在沿水槽方向布设了13支波高计,其中4支波高计安装在防波堤堤脚前及堤身上方,8支波高计安放在静水位以下的堤前缓坡地形上方,1支波高计安放在造波机前方的平底地形区域。海啸波作用到防波堤上的爬高位置采用波高计测量及目测同步进行,互相校核其观测结果。图1给出了试验布置示意图。
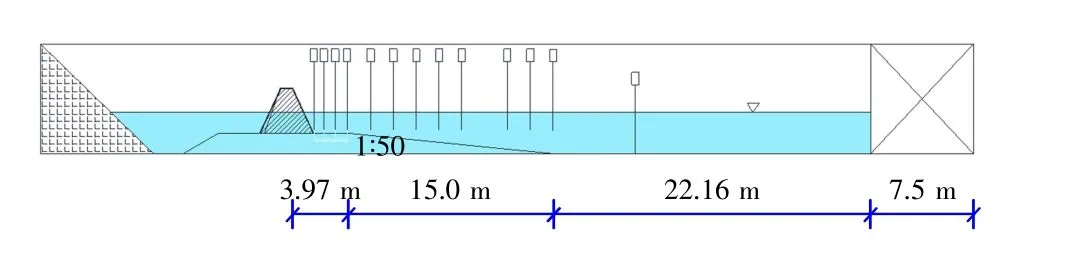
图1 海啸波沿斜坡堤爬高试验仪器及模型布置图Fig.1 Instrument and model layout of tsunami wave run-up on sloping breakwater
1.3 试验模型
本次试验研究选取了11个有代表性的斜坡堤断面,分别考虑了1颐1.5和1颐2的护面坡度,护面结构选取了489 g扭王字块体、115 g扭王字块体、80~100 g大块石、40~50 g大块石以及栅栏板等形式。表1为各断面的结构形式说明,图2为试验的无防浪墙斜坡堤断面示意图。

表1 试验斜坡堤结构形式Table 1 Type list of test sloping breakwater
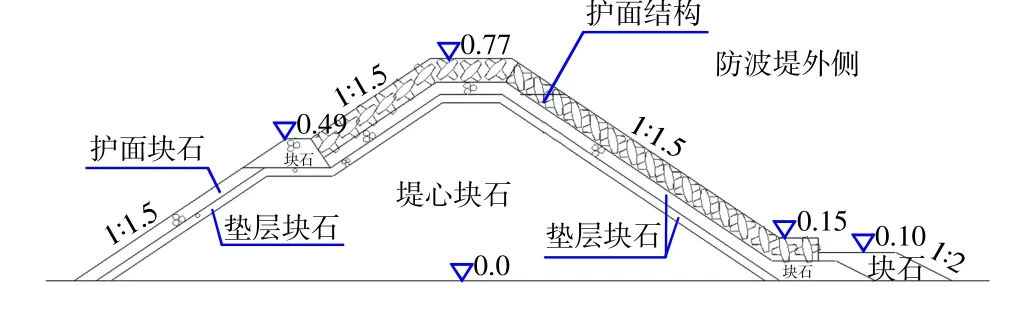
图2 无防浪墙斜坡堤断面示意图Fig.2 Schematic diagram of sloping breakwater without wall
1.4 试验工况
为了在防波堤堤前得到更大范围的波高水深比,所有斜坡堤均安放在1/50斜坡后方的平台上,平台高度为30 cm,堤前水深d设计了3种工况,分别为0.2 m、0.3 m及0.45 m,对应的造波板前水深分别为0.5 m,0.6 m和0.75 m。定义防波堤前海啸波高为H,不同水深下堤前波高水深比范围可达到0.07~1.24范围内,每个试验断面分别进行了28组试验,试验工况详见表2。
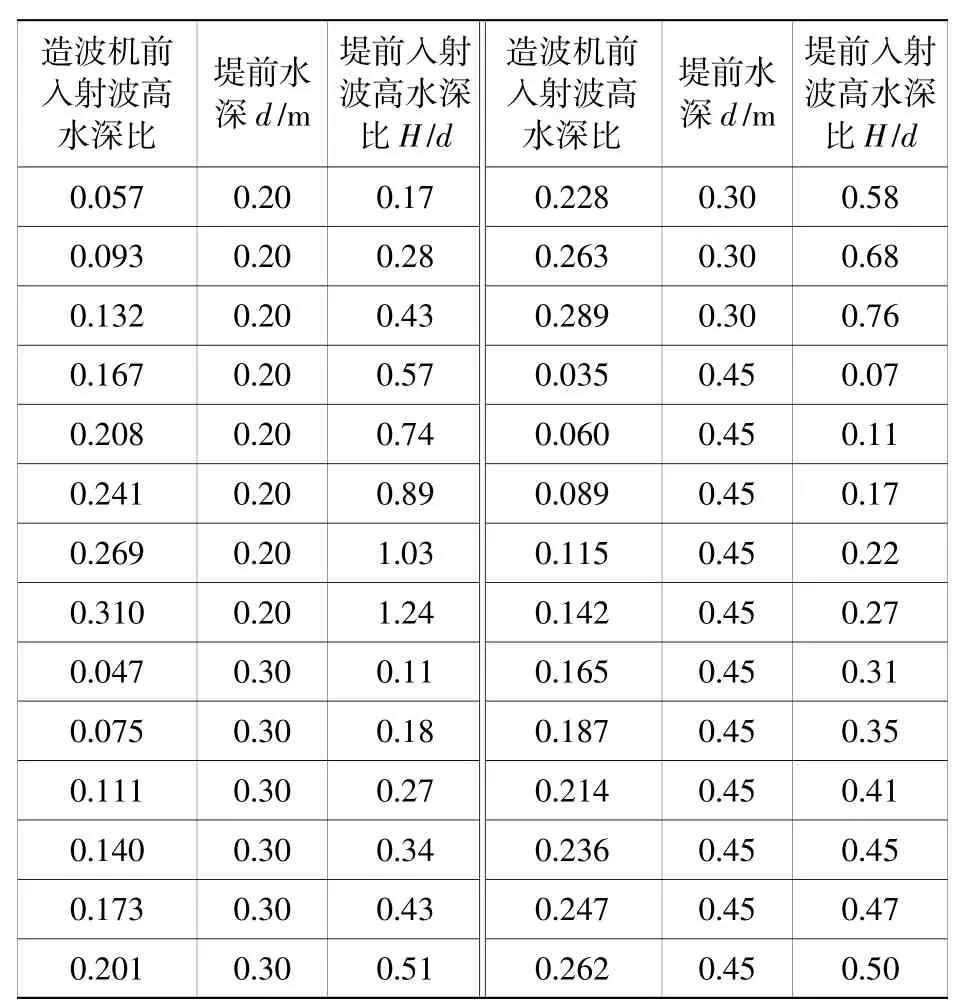
表2 试验水深、波高工况组合Table 2 Test conditions of water depth and wave height
1.5 试验海啸波(孤立波)模拟
本次试验采用水槽中生成孤立波来模拟海啸波,目前孤立波的试验模拟普遍采用Goring(1978)的造波板运动计算方法[4]。理论波形与造波机实际造出的试验波形对比见图3。
另外孤立波的波速及流速在试验前也分别进行了验证,且与理论值符合较好,整体看,本次试验可以正确模拟孤立波。
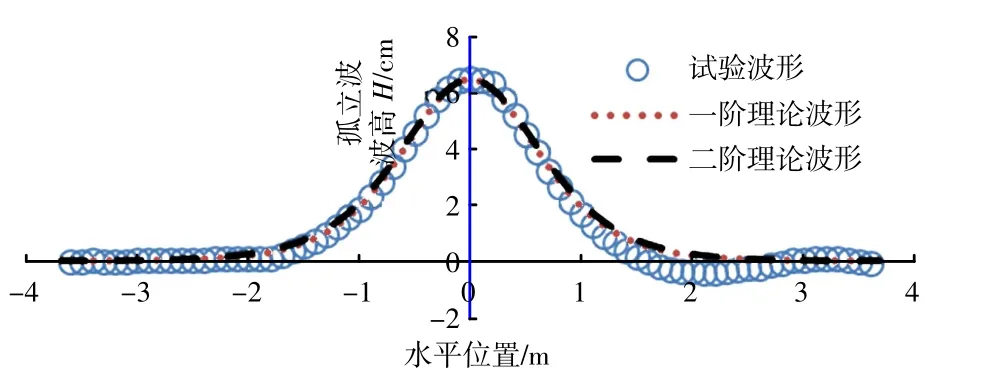
图3 试验波形及理论波形对比图Fig.3 Comparative diagram of test wave shape and theoretical wave shape
2 结果讨论
2.1 海啸波沿斜坡堤爬高特性分析
图4、图5分别给出坡度为1颐1.5以及1颐2的斜坡堤断面无量纲爬高测量结果,并且与Synolakis(1987年)[2]理论推导海啸波爬坡高度公式进行了对比,其中定义R为海啸波爬坡高度。根据临界破碎估算公式计算出临界破碎的堤前波高水深比,即1颐1.5坡度和1颐2坡度临界破碎波高水深比分别为0.52和0.38。由图中结果可以看出在波高水深比小于临界破碎值时,斜坡堤上爬坡与Synolakis(1987年)[2]提出的公式估算值整体趋势基本一致,均略有偏小,这种情况应该是本研究不同护面层的糙渗系数影响所致。
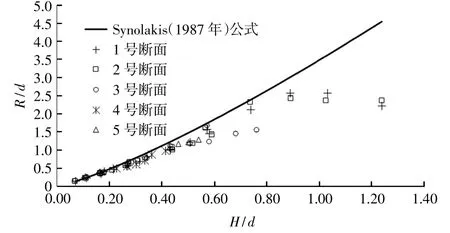
图4 坡度为1颐1.5斜坡堤海啸波最大无量纲爬高Fig.4 Tsunami maximum dimensionless climbing height of seawall with a slope of 1颐1.5

图5 坡度为1颐2斜坡堤海啸波最大无量纲爬高Fig.5 Tsunami maximum dimensionless climbing height of seawall with a slope of 1颐2
2.2 海啸波沿斜坡堤最大爬高经验公式
由图4、图5可以看出海啸波爬高的实测结果在波浪临界破碎前后的规律不甚相同,研究学者把爬高经验公式分为波浪非破碎以及破碎两种情况。在现实中通常叠加天文高潮情况下海啸爬高漫顶的危害更大,这时通常波高水深比较小,不会发生破碎,因此本研究采用波浪未破碎的爬高数据进行拟合,得到海啸波沿斜坡堤最大的爬高拟合公式。
本文利用Synolakis(1987年)[2]提出的爬高估算公式与本次试验中未发生越浪的数据进行相关性分析,见图6,经计算判定系数为0.880 8。
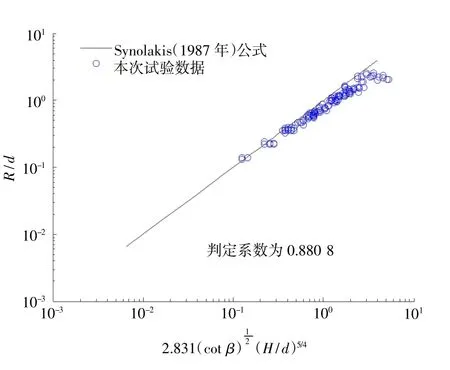
图6 Synolakis(1987年)公式与本次试验数据相关性分析Fig.6 Correlation analysis between Synolakis(1987 年)formula and test data of this paper
可以看到本次试验数据比Synolakis的估算公式略偏小,但整体规律较一致。试验观察不同护面形式的无量纲化爬高由小到大排序为:489 g扭王字块体<115 g扭王字块体<栅栏板(80~100 g块石)<40~50 g块石。可以发现不同种类的护面块体对爬高有明显影响,故本文在Synolakis推算的爬高函数形式基础上,增加了一个描述护面块体的糙渗系数K驻。经过最小二乘法的非线性拟合得到海啸波沿不同护面结构形式的斜坡堤最大爬高经验公式,其形式为:
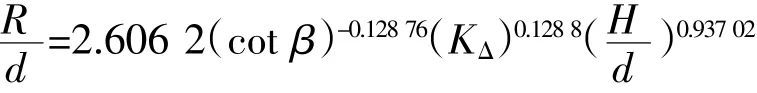
式中:d为堤前水深;H为堤前海啸波高;茁为斜坡的坡度角。经过拟合其判定系数可达到0.932,K驻对于扭王字块体、栅栏板、块石分别取0.47、0.50和0.55[2],拟合的相关性分析见图7。
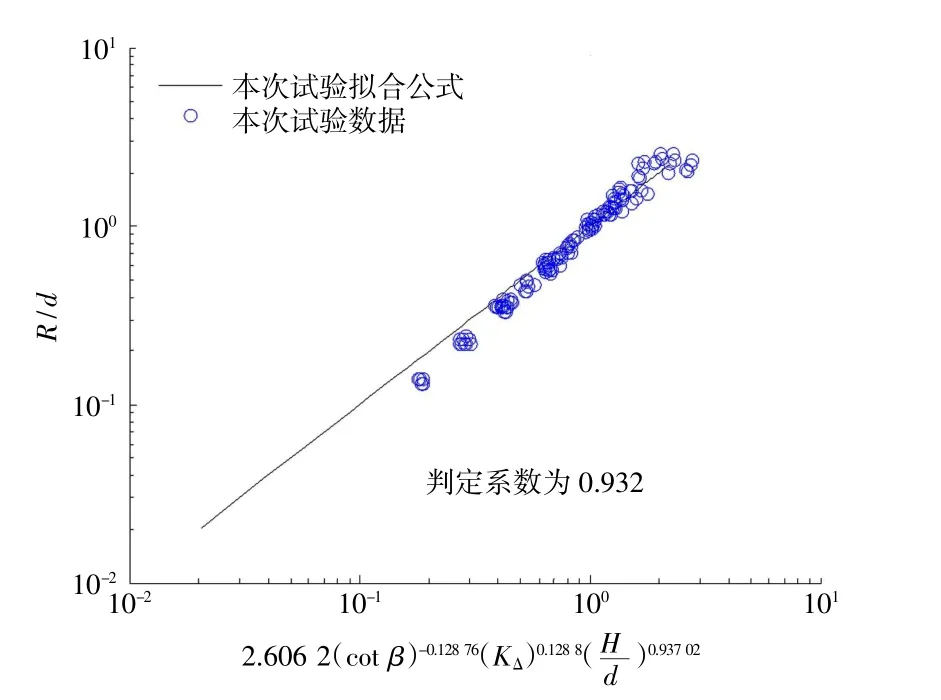
图7 本文拟合公式与本次试验数据相关性分析Fig.7 Correlation analysis between fitting formula and test data in this paper
经过数据分析,发现对于斜坡堤坡度角在1.5~2的断面来说,堤前波高水深比小于0.3的情况下,Synolakis(1987年)[2]的估算公式更接近实测值,本次拟合公式比实测值偏大;但是随着波高水深比的增大本次试验拟合的结果更接近实测值,因此在工程设计使用时,应根据实际海啸波情况选择适当的估算方法。
3 结语
本次研究在无反射造波水槽中产生孤立波模拟海啸,作用在斜坡式防波堤,得到了扭王字块、栅栏板和大块石3种护面结构,1颐1.5以及1颐2两种坡度下的试验数据。经分析得到以下主要结论:
1)堤前波高水深比小于临界破碎值时,斜坡堤上爬坡高度与Synolakis(1987年)[2]提出的公式估算值整体趋势基本一致,但均略有偏小。
2)通过最小二乘法拟合海啸波沿斜坡堤爬高的试验数据,考虑不同护面的糙渗系数影响,提出了新的海啸波沿斜坡堤最大爬高的估算公式,其判定系数为0.932。
3)本次研究的斜坡堤断面组数还比较少,下一阶段需要更多的水槽试验对不同坡度、更多类型护面块体、不同重量的结构断面进行研究,对本文新提出的公式进行逐步修正。
