基于Kriging代理模型的复杂精馏系统操作参数优化
2020-01-15刘思乐王修纲李德豹
刘思乐,王修纲,吴 静,3,李德豹
(1.沈阳科技学院化学工程系,沈阳 110167;2.上海交通大学化学化工学院;3.沈阳化工大学化学工程学院)
常减压蒸馏系统是炼油生产过程中重要的一次加工装置[1-3]。作为整个炼化企业的龙头装置,常减压蒸馏系统的优化运行直接关系到企业的整体经济效益。然而,由于所获取的原油属性及所需要的终端产品会随着市场行情的变化而变化,故炼化企业的加工方案会频繁变化,与之相对应的常减压蒸馏系统的操作方案也需要经常调整。于是,根据实际的生产情况优化设定常减压蒸馏系统的操作参数,使其能够长期保持在最优运行状态就显得十分重要。
目前,基于过程严格机理模型的操作参数优化技术主要采用传统的梯度类优化算法进行求解,如文献[4-6]中广泛使用的序列二次规划(SQP)。该类方法利用了过程模型的梯度类信息进行有向寻优,具有收敛速度快、寻优结果稳定等优势。然而,该类算法也存在以下不足:对初始值敏感,易于陷入局部最优,且迭代计算时需要反复对目标函数和约束条件进行求导。随着人工智能的不断发展,各种智能优化算法层出不穷,如遗传算法(GA)[7-8]、粒子群优化(PSO)[9-10]、模拟退火(SA)[11]、差分进化(DE)[12-13]等。由于智能类算法不需要知道过程对象的梯度信息,且拥有良好的全局寻优能力,现已被广泛应用于各类工程优化问题的求解[14-15]。
智能类优化算法的全局寻优能力是以大规模评价目标函数及约束条件为代价的,这对于拥有非线性、高维度、强耦合关系的复杂工业过程参数寻优十分不利。于是,建立一个可描述主要过程变量间变化关系的代理模型,并在优化问题求解时利用该模型代替原模型,就成为了一种降低计算成本的途径。于是,基于人工神经网络(ANN)[16]、径向基函数(RBF)[17]、多项式响应面(PRS)[18]、Kriging Surrogate[19-20]等的代理优化算法不断出现,且部分研究成果现已成功应用于各类实际的工程优化中。由于常减压蒸馏系统的过程变量极多,且变量间的耦合关系极强,因此,建立该类分离系统的代理模型十分困难,基于代理模型进行复杂精馏系统操作参数的优化求解也鲜有报道。本课题以东北某炼油厂实际的常减压蒸馏系统为背景,利用Aspen HYSYS建立装置平衡态的严格机理模型,并根据实际的生产需求建立装置中常压蒸馏塔(简称常压塔)的Kriging代理模型,用于快速寻找其操作参数的全局最优解。
1 常减压蒸馏系统的全流程模拟
Aspen HYSYS[21]是典型的流程模拟软件,该软件以物料平衡、能量平衡、焓平衡为基础,结合必要的物质流信息及其相对应的热力学计算公式,在特定的压力、温度、流速下可建立各类典型生产过程的各种严格机理模型[22-25]。常减压蒸馏系统是典型的炼油装置,国内外学者就其所研究的特定精馏系统,分别从全流程模拟、运行参数优化的角度建立起了不同的严格机理模型[26-28]。本课题以所选炼油厂的常减压蒸馏装置为背景,结合课题研究内容的需要,建立了如图1所示的常减压蒸馏系统全流程模拟平台。
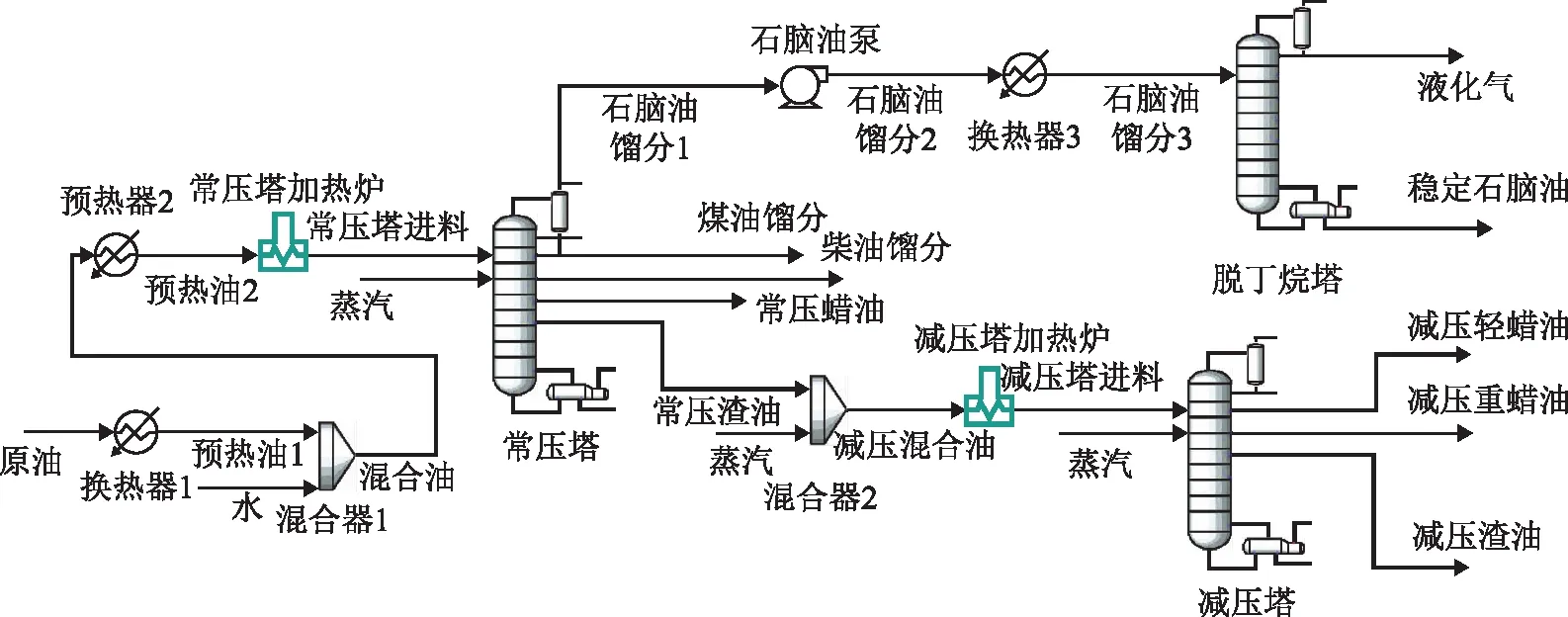
图1 基于Aspen HYSYS的常减压蒸馏系统流程模拟
所建常减压蒸馏系统全流程模拟平台可用于模拟进料油属性变化、操作条件变化对装置各侧线产品收率的影响,其主要的系统参数如表1所示。
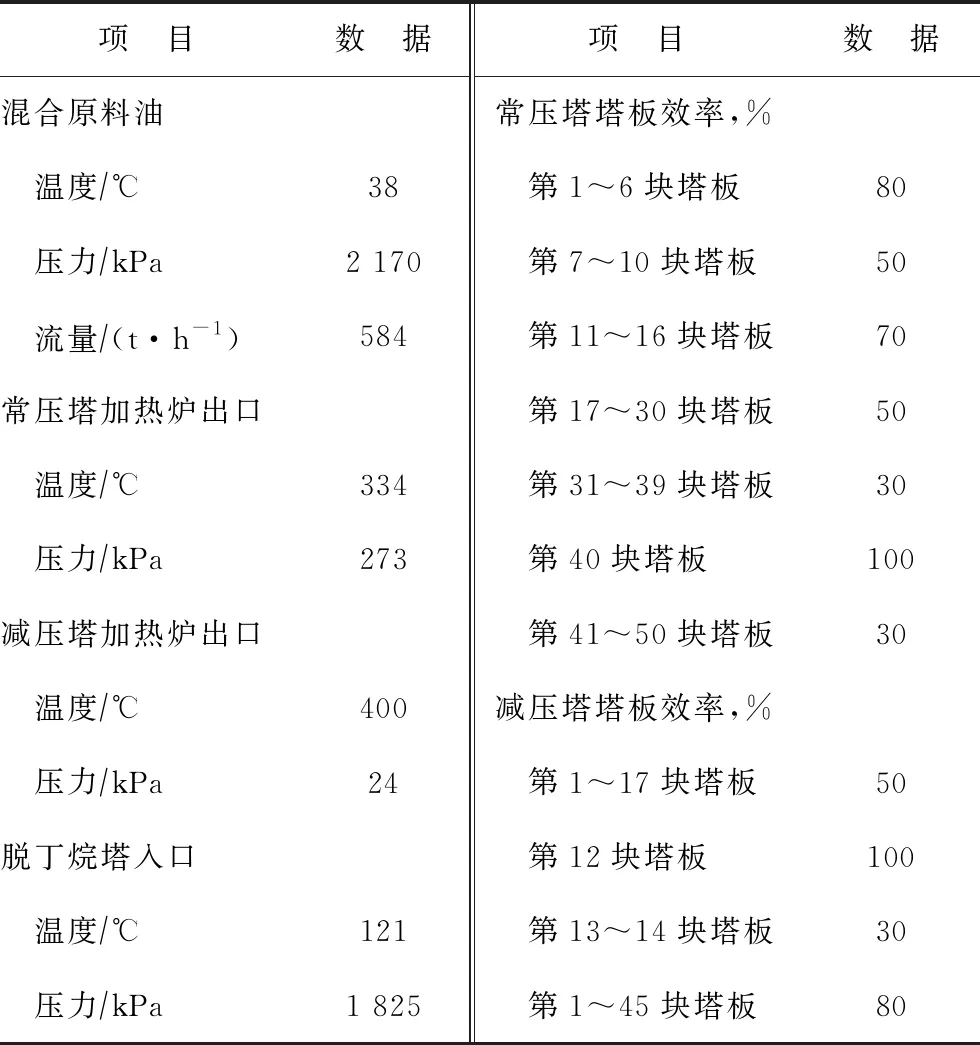
表1 常减压蒸馏系统全流程模拟平台的主要参数
2 常压蒸馏系统的Kriging代理模型
精馏是对混合物进行分离提纯的常规方法,该方法根据特定温度下不同的组分拥有不同的气相分压特性,可使液相中的轻组分转移到气相,气相中的重组分转移到液相,实现混合物中轻重组分的分离。精馏过程严格满足守恒定律,其机理模型可采用物料守恒方程(M方程)、气液相平衡方程(E方程)、归一方程(S方程)及焓守恒方程(H方程)共同描述,即采用MESH方程组描述。以如图2所示的精馏塔中第j块塔板为例,在假定精馏塔与外界环境绝热、每块塔板都处于热力学平衡的条件下,该塔板的MESH方程组可表示为:
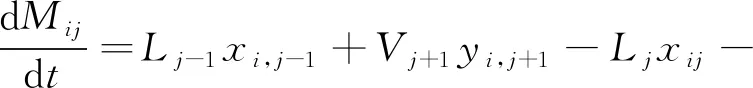
(1)
yij=Kijxij(i=1,…,c)
(2)
(3)
(4)
式中:Kij表示第j块塔板上第i种物质的气液相平衡常数;Lj和Vj分别是第j块塔板流出的液相、气相的流率,molh;xij和yij分别是第j块塔板上组分i的液相、气相的摩尔分数,%;Mij是第j块塔板上组分i的液相、气相总的物质的量,mol;Uj是第j块塔板上液相、气相的总能量,kJh;hL和hV分别是液相、气相的单位摩尔焓,kJmol;下标j-1和j+1分别表示第j块塔板的上一层塔板和下一层塔板。
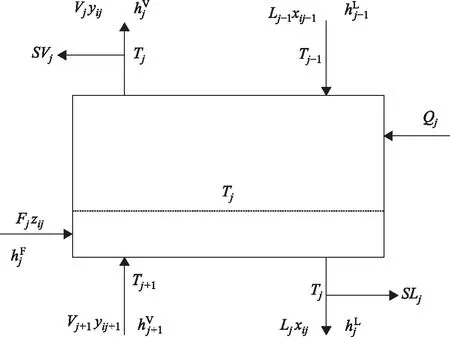
图2 第j块精馏塔板的平衡级示意
由式(1)~式(4)可知,对于一个拥有N种组分、M层塔板的精馏塔而言,其严格的机理模型至少需要(4N+9)×M个方程组进行描述。对于本课题所研究的常压精馏塔,除去其他必要的物性关联式外,N为51,M为50,共有10 650个方程组需要同时求解。显然,基于该严格的机理模型进行操作参数的实时优化必将十分耗时,因此,建立所关注过程变量间的函数关系模型,并基于新的代理模型进行参数优化十分重要。
2.1 Kriging模型简介
Kriging建模技术[29]是由著名地质学家Krige于1951年首次提出的,该技术现已被广泛应用于生化环境监测、PM2.5预报、石油化工、航空航天等领域。Kriging模型包括用于描述确定性关系的多项式回归部分和用于描述不确定性关系的统计误差部分,具体的Kriging代理模型如式(5)所示。
(5)

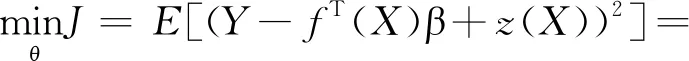
E[(Y-fT(X)β-σ2R(θ,w,X))2]
(6)
约束条件:θmin≤θ≤θmax
式中:X和Y分别为Kriging代理模型的输入和输出数据集;z(X)表示输入数据集的分布状态。利用最大似然估计法求取模型的期望值E,可估计出使式(6)最小的系统参数θ,其中θmin和θmax分别为所选系统参数θ的上界和下界。将所获取的系统参数代入式(5),并利用最小二乘法对Kriging代理模型的回归系数β进行估计,所得结果如下:
β=(fTR-1f)-1fTR-1Y
(7)
式中,R-1为所选分布状态相关系数R(θ,w,X)的逆,其他参数同上。
2.2 常压蒸馏系统的Kriging代理模型
由1.1节可知,常压蒸馏系统的作用是将混合原料油中的石脑油馏分、煤油馏分、柴油馏分、常压蜡油馏分切割出来,并通过管网将其输送至相对应的二次加工装置,用于后续的生产。因此,针对实际的生产任务,优化常压蒸馏系统的操作参数可实现特定侧向馏分油抽出量的升降,其关键操作参数和主要输出变量如表2和表3所示。为了保证各侧线所抽出的馏分油质量合格,在流程模拟中通常指定侧线产品的95%馏出温度。本课题所指定的关键馏分的95 %馏出温度(ATST D86方法)如表4所示。
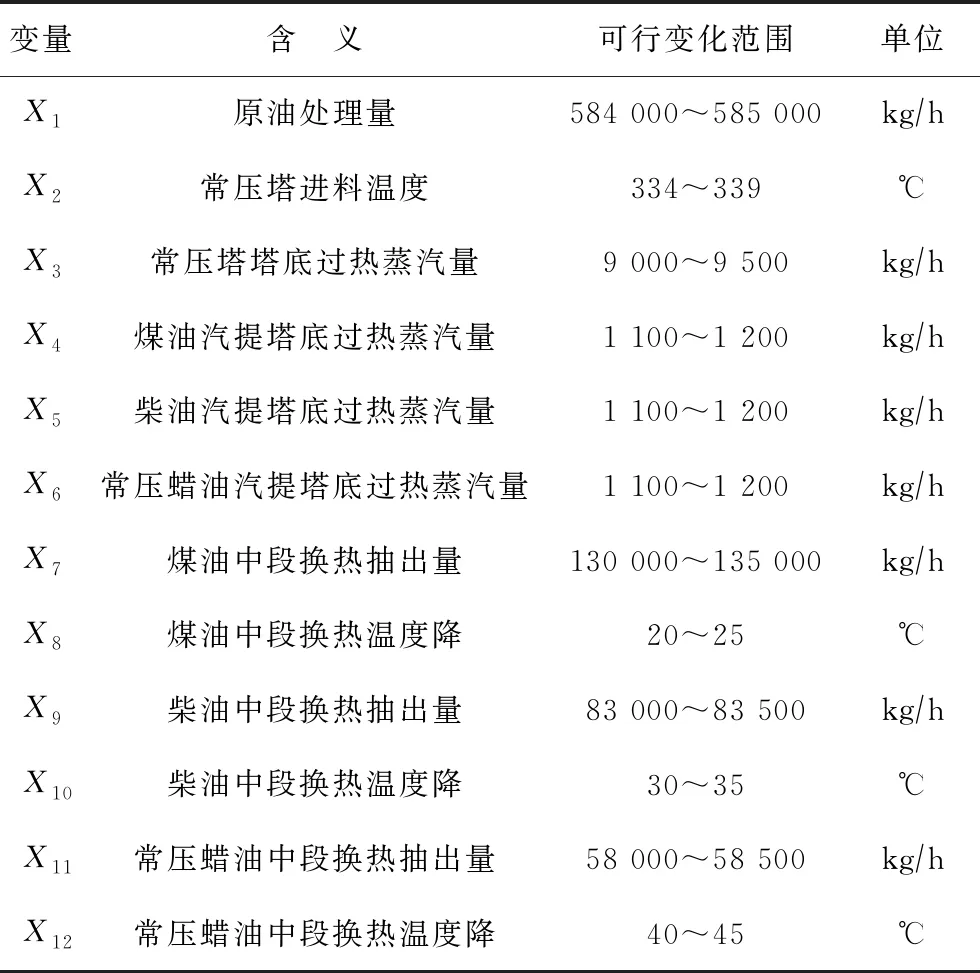
表2 常压蒸馏系统的关键操作参数

表3 常压蒸馏系统的主要输出变量

表4 关键馏分的95 %馏出温度
用Matlab 与 Aspen HYSYS接口,根据拉丁超立方采样(LHS)规则,从所建常减压蒸馏系统的全流程模拟平台中采200组样本。随机选取其中的150组样本作为训练集建立常压蒸馏系统的Kriging代理模型,剩余的50组样本作为测试集,用以验证所建Kriging代理模型的精度,预测结果的平均相对误差(ARE)如表5所示。

表5 Kriging代理模型测试集的平均相对误差
由表5可知,所建Kriging代理模型可准确反映常压蒸馏系统操作参数的变化对其各侧线产品抽出量的影响(最大平均相对误差为0.008 9)。基于所建Kriging代理模型进行操作参数优化,可避免大规模非线性MESH方程组的反复求解,是提高常减压蒸馏装置操作参数优化效率的一种途径。
3 基于常压蒸馏系统Kriging代理模型的操作参数智能优化
由2.2节可知,常压蒸馏系统的操作参数优化问题可表述为:通过优化表2所述的12个关键操作变量X=[X1,…,X12],使得表3中各侧线馏分油的抽出量Y=[Y1,…,Y4]与其设定值Yset的误差平方和最小。其具体的数学表达式为:
(8)
式中:Ki为所建关于第i个输出变量的Kriging代理模型,Xmin,i和Xmax,i分别为决策变量的最小值和最大值,决定了整个寻优空间。
3.1 粒子群优化
粒子群优化(PSO)[30-31]是一种经典的群智能算法。该算法模拟了鸟类的觅食行为,具有很强的全局寻优能力。PSO结构设计简单、参数数量较少,一经提出,便被广泛应用于各类优化问题的求解。该算法的实施通过如下2个算子迭代进行。
Vk,i=wk,iVk-1,i+C1R1(Pbest,i-Xk,i)+
C2R2(Pbest,g-Xk,i)
(9)
Xk+1,i=Xk,i+Vk,i
(10)
式中:Vk,i和Xk,i分别表示第i个粒子在第k次迭代时的移动速度和位置;Pbest,i和Pbest,g分别表示第i个粒子和全部粒子在第k次迭代时的最优值;wk,i表示第i个粒子在第k次迭代时的惯性因子,可继承以前的速度;C1和C2分别为自我认知因子和社会认知因子,通常取常数;R1和R2分别为服从高斯分布的随机数,可帮助种群在更广泛的空间中随机寻优。PSO的具体寻优步骤如图3所示。其中,iter和Iter表示迭代次数。
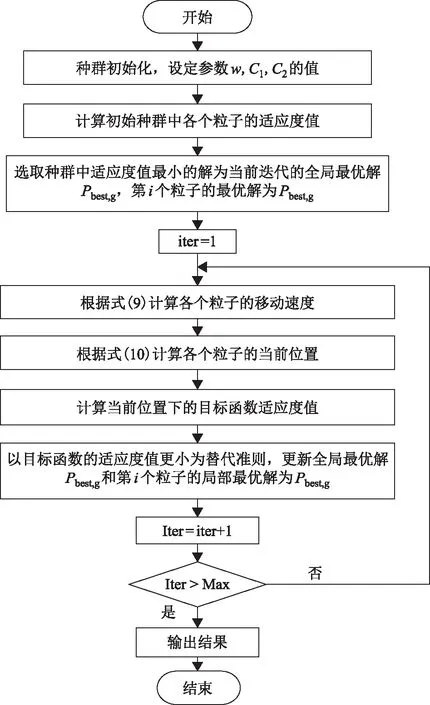
图3 PSO的流程图
3.2 基于PSO的操作参数优化
针对式(8)所述常压蒸馏系统的操作参数优化问题,本课题选取基本PSO作为搜索引擎,在表2所示的操作参数空间中进行迭代寻优,具体的参数设置:wk,i为1,C1为0.5,C2为0.5。根据炼化厂的实际生产需求,要求常压蒸馏系统切割出的石脑油馏分、煤油馏分、柴油馏分、常压蜡油馏分的质量流速分别为23,122,121,23 th,即设定Y1,set为23 000、Y2,set为122 000、Y3,set为121 000、Y4,set为23 000。经过10 000次迭代寻优后,所获常压蒸馏系统的关键操作参数如表6所示,具体的迭代过程目标函数收敛情况如图4所示。
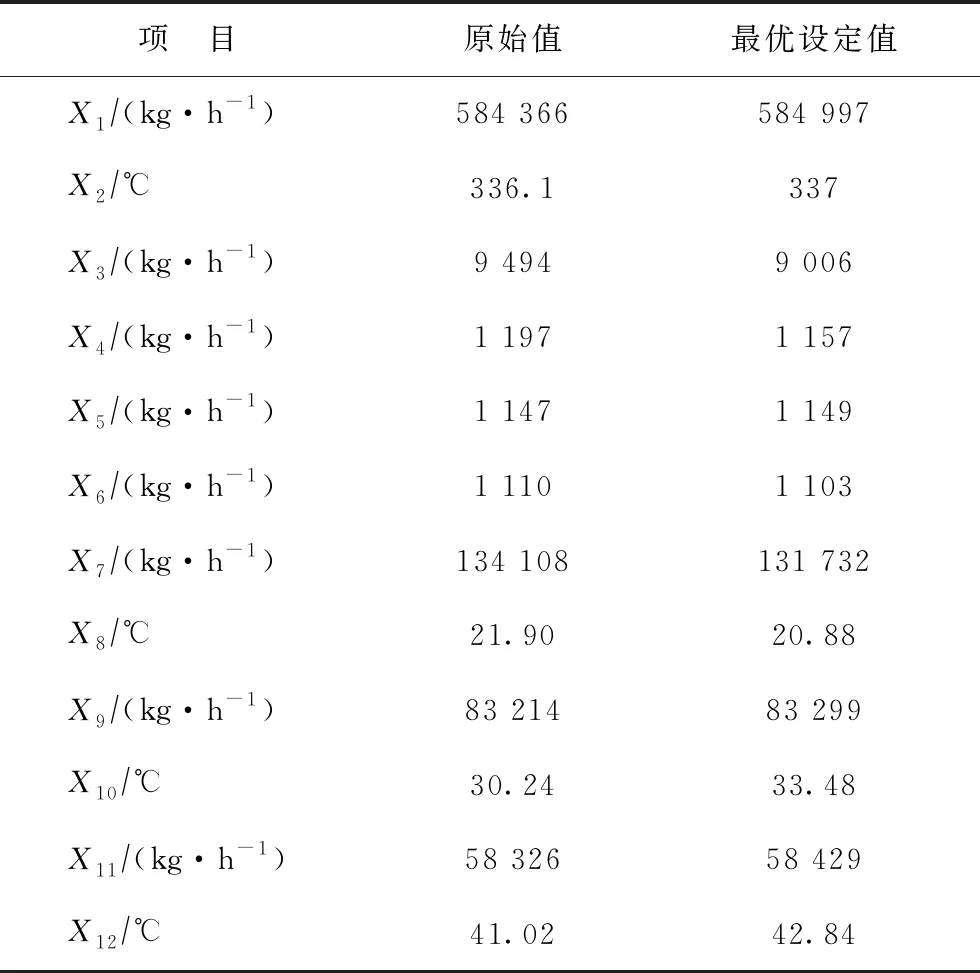
表6 基于Kriging代理模型的操作参数寻优结果
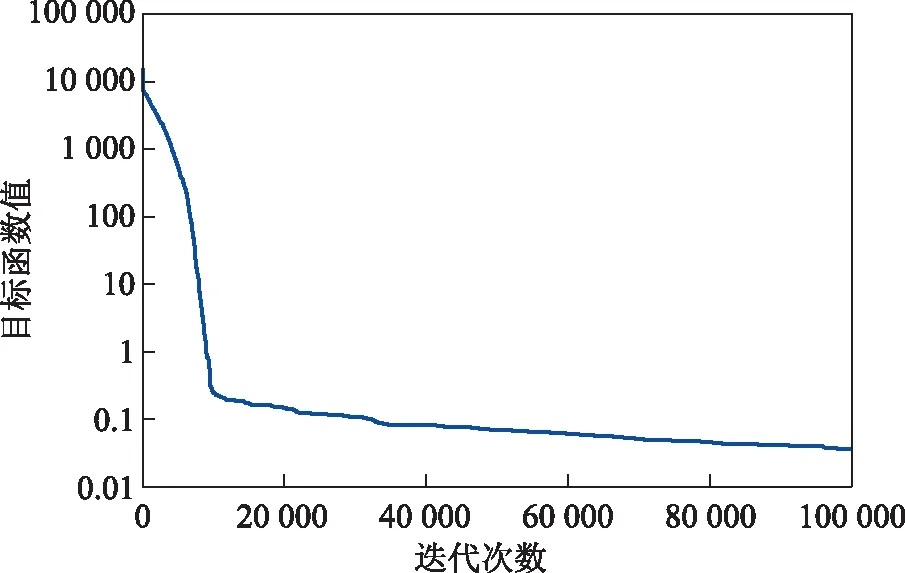
图4 目标函数的迭代寻优结果
由于使用了Kriging代理模型来描述关键操作变量与主要输出变量间的关系,可有效避免PSO迭代寻优过程中反复求解常压蒸馏系统的大规模MESH方程组,故本课题所提方法可以大幅度节约时间成本。利用所建常减压蒸馏系统全流程模拟平台,分别采用基于严格机理模型的传统寻优方法和基于所提Kriging代理模型的优化方法进行操作参数寻优,经多次试验可知,传统方法大约需要数个小时,而本课题方法可在5 min内给出寻优结果,所提方法完全满足炼化企业对寻优算法的实时性要求。将上述常压蒸馏系统的最优操作参数代入所建常减压蒸馏系统的全流程模拟平台,所得模拟结果如表7所示。由表7可知,所寻找到的常压蒸馏系统操作参数可基本满足该企业的生产任务,其最大相对误差为1.4%。该误差对于实际的生产过程不会产生过大的影响,所得结果可应用于实际的常压蒸馏操作参数优化设定系统。
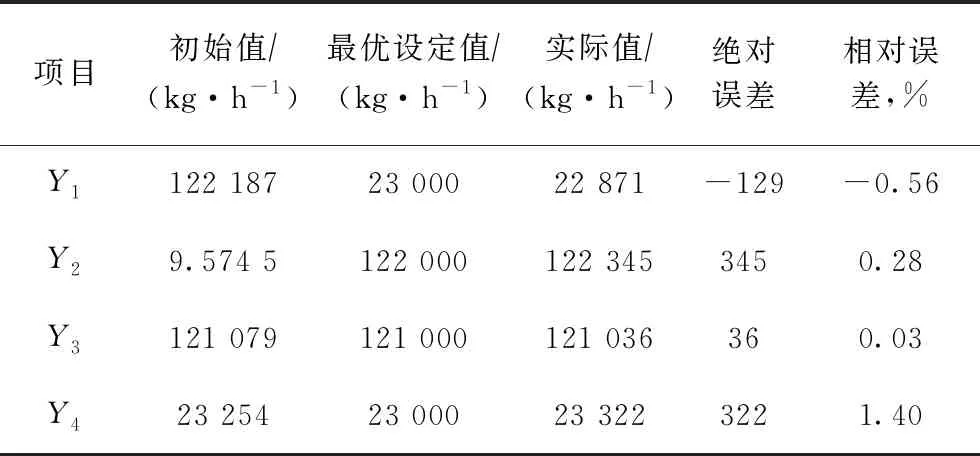
表7 常压蒸馏系统各侧线馏分油抽出量的误差统计
4 结 论
针对以常压蒸馏系统严格机理模型为过程约束条件的操作参数优化问题计算耗时的情况,提出了一种基于Kriging代理模型的常压蒸馏系统操作参数智能优化方法。该方法利用Kriging模型代替常压蒸馏系统的严格机理模型,使用粒子群优化(PSO)算法进行全局寻优,可在较短的时间内找到满足生产需求的全局最优解。基于Aspen HYSYS的仿真试验证明了所提方法的有效性,未来可将该方法扩展至常减压蒸馏系统的全流程,同时还可以考虑进料油属性变化后的操作参数全流程优化设定问题。
