BE-代数的直觉Q-模糊理想

王丰效

(喀什大学 数学与统计学院, 新疆 喀什 844000)

自Zadeh创立了模糊集理论以来[1]，众多学者讨论了模糊集的推广.作为模糊集的推广，Atanassov提出直觉模糊集的概念及相关理论[2-3].随后，模糊集和直觉模糊集被广泛应用于各类代数系统.作为BCK-代数的推广，文献[4]引入BE-代数的概念，讨论了它的相关性质.文献[5]给出BE-代数理想的概念及其相关性质，并给出了BE-代数理想的刻画. 文献[6-7]将模糊集的概念应用于BE-代数，讨论BE-代数的模糊子代数和模糊理想及其相关性质. 文献[8]讨论BE-代数的模糊滤子的相关特征.文献[9]引入BE-代数的Doubt-模糊理想的概念，并讨论其相关性质. 论文将直觉Q-模糊集的概念应用于BE-代数, 给出BE-代数的直觉Q-模糊理想概念, 并讨论其基本性质.

为讨论问题方便,下面先给出一些相关的概念.

代数系统(X,*,1)如果满足下列公理,即对∀x,y,z∈S,都有：(1)x*x=1；(2)x*1=1；(3)1*x=x； (4)x*(y*z)=y*(x*z).则称(X,*,1)为BE-代数，简称X是一个BE-代数[4].

始终约定X表示BE-代数(X,*,1). 在X上可以定义偏序关系≤：x≤y⟺x*y=1.假设(X,*,1)为BE-代数，则对任意x,y∈X,有x*(y*x)=1,y*((y*x)*x)=1.若(X,*,1)是BE-代数，如果对任意x,y,z∈X,有y*z≤(x*y)*(x*z),则称(X,*,1)为传递BE-代数.如果对任意x,y,z∈X,有x*(y*z)=(x*y)*(x*z),则称(X,*,1)为自分配BE-代数.

设A是BE-代数(X,*,1)的非空子集，如果对任意x,y∈A,有x*y∈A,则称A为BE-代数(X,*,1)的子代数.

定义1[5]设I是BE-代数X的非空子集, 如果: (1) ∀x∈X,a∈I,有x*a∈I；(2) ∀x∈X,a,b∈I,有(a*(b*x))*x∈I.则称I是BE-代数X的理想.

给定一个集合Q,称μ:X×Q→[0,1]为X上的Q-模糊集. 对任意t∈[0,1],集合Uq(μ,t)={x∈X|μ(x,q)≥t}称为μ关于Q的上水平截集，集合Lq(μ,t)={x∈X|μ(x,q)≤t}称为μ关于Q的下水平截集.

定义2[7]设μ是X的模糊子集,若对∀x,y,z∈X,都有:(1)μ(x*y)≥μ(y)；(2)μ((x*(y*z))*z)≥μ(x)∧μ(y).则称μ是X的模糊理想.

设X为非空集,A={|0≤αA(x)+βA(x)≤1,x∈X}称为X上的直觉模糊集，其中αA(x),βA(x)是X上的模糊集，分别表示X上的元素属于A的隶属度和非隶属度.为了方便起见，将直觉模糊集A简记为A=(αA,βA).

1 BE-代数的直觉模糊理想

为了方便起见，用X表示BE-代数(X,*,1), 并假定Q是给定的一个集合. 设X为非空集，A={|0≤αA(x,q)+βA(x,q)≤1,x∈X,q∈Q}称为X上的直觉Q-模糊集，其中αA:X×Q→[0,1],βA:X×Q→[0,1]是X上的Q-模糊集. 为了方便起见，将直觉Q-模糊集A简记为A=(αA,βA).对任意t∈[0,1],集合Uq(αA,t)={x∈X|αA(x,q)≥t}称为A关于Q的上水平截集，集合Lq(βA,t)={x∈X|βA(x,q)≤t}称为A关于Q的下水平截集.

定义3设A=(αA,βA)是BE-代数X上的直觉Q-模糊集,若∀x,y,z∈X，q∈Q,都有

(1)αA(x*y,q)≥αA(y,q)；

(2)βA(x*y,q)≤βA(y,q)；

(3)αA((x*(y*z))*z,q)≥αA(x,q)∧αA(y,q)；

(4)βA((x*(y*z))*z，q)≤βA(x,q)∨βA(y,q).

则称A是X的直觉Q-模糊理想.

例1假设X={1,a,b,c,d,e},X上的二元运算“*”见表1.

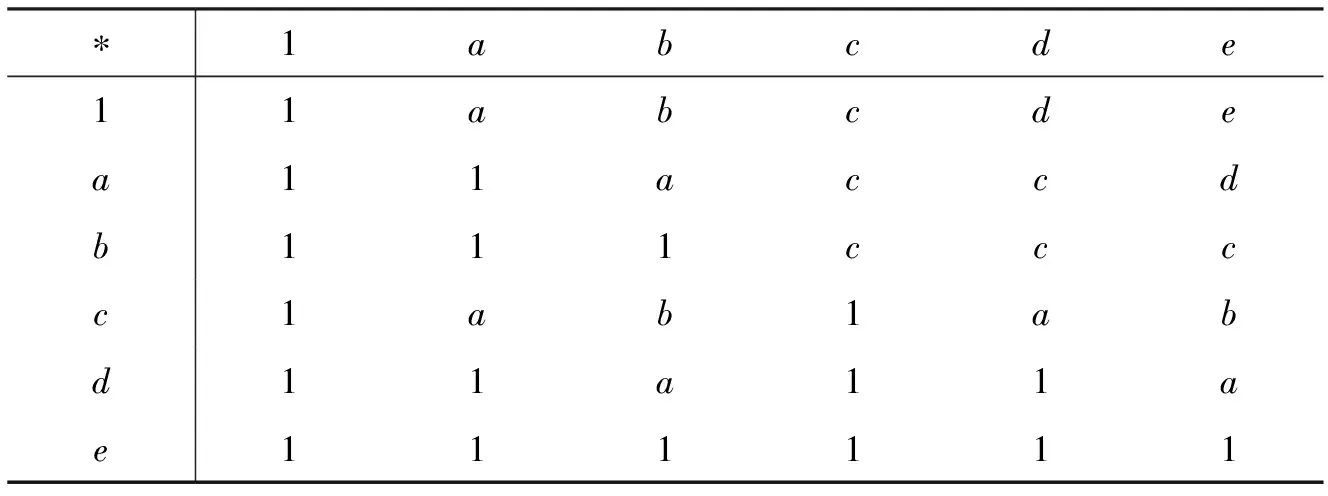
表1 X上的二元运算

容易验证(X,*,1)是BE-代数. 对给定集合Q={q1,q2},在X上的Q-直觉模糊集A=(αA,βA)为

αA(1,q1)=αA(a,q1)=αA(b,q1)=0.3,αA(c,q1)=αA(d,q1)=αA(e,q1)=0.8,

βA(1,q1)=βA(a,q1)=βA(b,q1)=0.69,βA(c,q1)=βA(d,q1)=βA(e,q1)=0.18,

αA(1,q2)=αA(a,q2)=αA(b,q2)=0.35,αA(c,q2)=αA(d,q2)=αA(e,q2)=0.85,

βA(1,q2)=βA(a,q2)=βA(b,q2)=0.73,βA(c,q2)=βA(d,q2)=βA(e,q2)=0.22.

则A=(αA,βA)是X上的直觉Q-模糊理想.

如果对给定集合Q={q},定义X上的Q-直觉模糊集B=(αB,βB)满足

αB(1,q)=αB(a,q)=0.4,αB(b,q)=αB(c,q)=αB(d,q)=αB(e,q)=0.6，

βB(1,q)=βB(a,q)=αB(b,q)=0.56,βB(c,q)=βB(d,q)=βB(e,q)=0.38.

则αB((a*(a*b))*b,q)=αB((a*a)*b,q)=αB(b,q)=0.6>0.4=αB(a,q)∨αB(a,q). 故直觉Q-模糊集B=(αB,βB)不是X上的直觉Q-模糊理想.

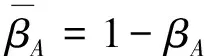
证明由于A=(αA,βA)是BE-代数X上的直觉Q-模糊理想，易知模糊集αA是X的Q-模糊理想. 对任意x,y,z∈X,q∈Q,有

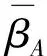
综上，由定义3可得A=(αA,βA)是BE-代数X上的直觉Q-模糊理想.

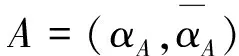
定理3如果A=(αA,βA)是传递BE-代数X上的直觉Q-模糊集，则A=(αA,βA)是X上的直觉Q-模糊理想，当且仅当对任意x,y,z∈X,有

(1)αA(1,q)≥αA(x,q),βA(1,q)≤βA(x,q);

(2)αA(x*z,q)≥αA(x*(y*z),q)∧αA(y,q),βA(x*z,q)≤βA(x*(y*z),q)∨βA(y,q).

证明假设A=(αA,βA)是BE-代数X上的直觉Q-模糊理想，因而由定义3可得，对任意x∈X,αA(1,q)=αA(x*x,q)≥αA(x,q),βA(1,q)=βA(x*x,q)≤βA(x,q). 由于BE-代数X是传递的，因而对任意x,y,z∈X,有(y*z)*z≤(x*(y*z))*(x*z),即

((y*z)*z)*((x*(y*z))*(x*z))=1,

所以,有

αA(x*z,q)=αA(1*(x*z),q)=αA((((y*z)*z)*((x*(y*z))*(x*z)))*(x*z),q)≥

αA(((y*z)*z),q)∧αA(x*(y*z),q)=αA(((y*(1*z))*z),q)∧αA(x*(y*z),q)≥

(αA(y,q)∧αA(1,q))∧αA(x*(y*z),q)=αA(y,q)∧αA(x*(y*z),q)=

αA(x*(y*z),q)∧αA(y,q)，

βA(x*z,q)=βA(1*(x*z),q)=βA((((y*z)*z)*((x*(y*z))*(x*z)))*(x*z),q)≤

βA(((y*z)*z),q)∨βA(x*(y*z),q)=βA(((y*(1*z))*z),q)∨βA(x*(y*z),q)≤

(βA(y,q)∨βA(1,q))∨βA(x*(y*z),q)=βA(y,q)∨βA(x*(y*z),q)=

βA(x*(y*z),q)∨βA(y,q).

如果A=(αA,βA)是传递BE-代数X上的直觉Q-模糊集，并且满足定理3的条件(1)，(2)，则对任意x,y,z∈X,q∈Q,有

αA(x*y,q)≥αA(x*(y*y),q)∧αA(y,q)=αA(1,q)∧αA(y,q)=αA(y,q)，

βA(x*y,q)≤βA(x*(y*y),q)∨βA(y,q)=βA(1,q)∨βA(y,q)=βA(y,q).

若a≤b,即a*b=1,故

αA(b,q)=αA(1*b,q)≥αA(1*(a*b),q)∧αA(a,q)=αA(1,q)∧αA(a,q)=αA(a,q)，

βA(b,q)=βA(1*b,q)≤βA(1*(a*b),q)∨βA(a,q)=βA(1,q)∨βA(a,q)=βA(a,q).

由于BE-代数X是传递的，因此对任意x,y,z∈X,有(y*z)*z≤(x*(y*z))*(x*z)，故

αA((y*z)*z,q)≤αA((x*(y*z))*(x*z),q),

βA((y*z)*z,q)≥βA((x*(y*z))*(x*z),q).

所以，有

αA((x*(y*z))*z,q)≥αA((x*(y*z))*(x*z),q)∧αA(x,q)≥

αA((y*z)*z,q)∧αA(x,q)≥αA((y*z)*(y*z),q)∧αA(y,q)∧αA(x,q)=

αA(1,q)∧αA(y,q)∧αA(x,q)=αA(x,q)∧αA(y,q)，

βA((x*(y*z))*z,q)≤βA((x*(y*z))*(x*z),q)∨βA(x,q)≤

βA((y*z)*z,q)∨βA(x,q)≤βA((y*z)*(y*z),q)∨βA(y,q)∨βA(x,q)=

βA(1,q)∧βA(y,q)∧βA(x,q)=βA(x,q)∧βA(y,q).

综上，由定义3可得A=(αA,βA)是X上的直觉Q-模糊理想.

定理4直觉模糊集A=(αA,βA)是X的直觉Q-模糊理想，当且仅当对任意t,s∈[0,1],X的非空子集Uq(αA,t)和Lq(βA,s)都是X的理想.

证明假设A=(αA,βA)是X的直觉Q-模糊理想. 如果存在t∈[0,1],使得Uq(αA,t)非空，因而一定存在a∈Uq(αA,t)，满足αA(a,q)≥t,从而对于任意的x∈X，有αA(x*a,q)≥αA(a,q)≥t,因而x*a∈Uq(αA,t).另外，假定a,b∈Uq(αA,t),则αA(a,q)≥t,αA(b,q)≥t. 因此∀x∈X，由定义3，有αA((a*(b*x))*x,q)≥αA(a,q)∧αA(b,q)≥t, 故(a*(b*x))*x∈Uq(αA,t),由定义1可知非空子集Uq(αA,t)是X的理想. 利用同样的方式可以证明非空子集Lq(βA,s)是X的理想.

反过来，如果对任意t,s∈[0,1],q∈Q,非空子集Uq(αA,t)和Lq(βA,s)都是X的理想. 假定存在c,d∈X，使得αA(c*d,q)<αA(d,q), 取t0∈[0,1]，满足αA(c*d,q)

如果存在x0,y0,z0∈X，使得αA((x0*(y0*z0))*z0,q)<αA(x0,q)∧αA(y0,q), 令

2t1=αA((x0*(y0*z0))*z0,q)+αA(x0,q)∧αA(y0,q)，

则x0,y0∈Uq(αA,t1),(x0*(y0*z0))*z0∉Uq(αA,t1). 由于x0,y0∈Uq(αA,t1),Uq(αA,t1)是X的理想，因此有(x0*(y0*z0))*z0∈Uq(αA,t1)，与(x0*(y0*z0))*z0∉Uq(αA,t1)矛盾,所以对任意的x,y,z∈X,q∈Q，有αA((x*(y*z))*z,q)≥αA(x,q)∧αA(y,q).类似可以证明对任意的x,y,z∈X,q∈Q，有βA((x*(y*z))*z,q)≤βA(x,q)∨βA(y,q).综上，由定义3可知直觉模糊集A是BE-代数X的直觉Q-模糊理想.

定理5假设I是BE-代数X的理想，则一定存在直觉Q-模糊集A=(αA,βA)和常数t,s∈[0,1]，使得Uq(αA,t)=Lq(βA,s)=I,并且A=(αA,βA)是BE-代数X的直觉Q-模糊理想.

证明假设I是BE-代数X的理想, 对于任意的q∈Q,定义X的直觉Q-模糊集A=(αA,βA)满足：当x∈I时，αA(x,q)=t,βA(x,q)=s；当x∉I时，αA(x,q)=βA(x,q)=0. 因此

Uq(αA,t)=Lq(βA,s)=I.

下证A=(αA,βA)是BE-代数X的直觉Q-模糊理想. 对任意x,y∈X,有

(1) 如果x∈X，y∈I,则x*y∈I,所以αA(x*y,q)=t=αA(y,q)；

(2) 如果x,y∉I,则αA(x,q)=αA(y,q)=0,即αA(x*y,q)≥0=αA(y,q)；

(3) 如果x∈I，y∉I,则αA(x,q)=t,αA(y,q)=0,从而αA(x*y,q)≥0=αA(y,q)；

(4) 如果x∉I，y∈I,则αA(x*y,q)=t,αA(y,q)=t,故αA(x*y,q)=t=αA(y,q).

综上，对任意x,y∈X,q∈Q,有αA(x*y,q)≥αA(y,q).

对任意x,y,z∈X,q∈Q，有

(1) 如果x,y∈I,则(x*(y*z))*z∈I,故αA((x*(y*z))*z,q)=t=αA(x,q)∧αA(y,q)；

(2) 如果x∉I或y∉I,则αA(x,q)=0或αA(y,q)=0,即αA(x,q)∧αA(y,q)=0,所以αA((x*(y*z))*z,q)≥0=αA(x,q)∧αA(y,q).因此对任意x,y,z∈X,有

αA((x*(y*z))*z,q)≥αA(x,q)∧αA(y,q).

利用同样对方法可以证明，对任意x,y,z∈X,q∈Q,有

βA(x*y,q)≤βA(y,q),βA((x*(y*z))*z,q)≤βA(x,q)∨βA(y,q).

因此A=(αA,βA)是BE-代数X的直觉Q-模糊理想.

定理6假设I是BE-代数X的子集，定义直觉Q-模糊集A=(αA,βA)，满足

αA(x,q)=1-βA(x,q)=λ,(x∈I,q∈Q,λ∈[0,1])，

αA(x,q)=1-βA(x,q)=0,(x∉I,q∈Q).

如果A=(αA,βA)是BE-代数X的直觉Q-模糊理想，则I是BE-代数X的理想.

证明假设A=(αA,βA)是BE-代数X的直觉Q-模糊理想. 对任意q∈Q,如果x∈X,a∈I,则αA(x*a,q)≥αA(a,q)=λ,从而x*a∈I.如果a,b∈I,则αA(a,q)=αA(b,q)=λ,并且αA((a*(b*x))*x,q)≥αA(a,q)∧αA(b,q)=λ,即(a*(b*x))*x∈I.因此I是BE-代数X的理想.

记A(a,b)={x∈X|a*(b*x)=1},并称A(a,b)为a和b的上集.易知对于BE-代数X，有1,a,b∈A(a,b).

引理1[5]BE-代数X的非空子集I是X的理想的充要条件是:

(1) 1∈I；

(2) ∀x,z∈X,∀y∈I,x*(y*z)∈I⟹x*z∈I.

定理7如果A=(αA,βA)是BE-代数X的直觉Q-模糊集，则A是X的直觉Q-模糊理想的充分必要条件是∀a,b∈X,∀s,t∈[0,1]，有

a,b∈Uq(αA,t)∩Lq(βA,s)⟹A(a,b)⊆Uq(αA,t)∩Lq(βA,s).

证明假设A=(αA,βA)是BE-代数X的直觉Q-模糊理想，如果a,b∈Uq(αA,t)∩Lq(βA,s),则a,b∈Uq(αA,t),a,b∈Lq(βA,s), 从而αA(a,q)≥t,αA(b,q)≥t,βA(a,q)≤s,βA(b,q)≤s. 若x∈A(a,b),则a*(b*x)=1,从而

αA(x,q)=αA(1*x,q)=αA((a*(b*x))*x,q)≥αA(a,q)∧αA(b,q)≥t，

βA(x,q)=βA(1*x,q)=βA((a*(b*x))*x,q)≤βA(a,q)∨βA(b,q)≤s，

所以，x∈Uq(αA,t),x∈Lq(βA,s),故A(a,b)⊆Uq(αA,t)∩Lq(βA,s).

另一方面，如果∀a,b∈X,a,b∈Uq(αA,t)∩Lq(βA,s)⟹A(a,b)⊆Uq(αA,t)∩Lq(βA,s),为了证明A=(αA,βA)是X的直觉Q-模糊理想，只需证明Uq(αA,t)和Lq(βA,s)都是X的理想. 首先，注意到对任意的a,b∈Uq(αA,t)∩Lq(βA,s)，有1∈A(a,b)⊆Uq(αA,t)∩Lq(βA,s),因此1∈Uq(αA,t),1∈Lq(βA,s).如果对任意的∀x,y,z∈X，有y∈Uq(αA,t),x*(y*z)∈Uq(αA,t). 注意到

(x*(y*z))*(y*(x*z))=(x*(y*z))*(x*(y*z))=1,

x*z∈A(x*(y*z),y)⊆Uq(αA,t),

如果

y∈Lq(βA,s),x*(y*z)∈Lq(βA,s),

则

x*z∈A(x*(y*z),y)⊆Lq(βA,s)，

即x*z∈Lq(βA,s).综上可得Uq(αA,t)和Lq(βA,s)都是X的理想.再由定理4可知A是BE-代数X的直觉Q-模糊理想.

假设A=(αA,βA)和B=(αB,βB)是X的直觉Q-模糊集，A和B的交A∩B=(αA∩B,βA∩B)，定义为

αA∩B(x)=αA(x)∧αB(x),βA∩B(x)=βA(x)∨βB(x).

定理8如果A=(αA,βA)和B=(αB,βB)都是BE-代数X的直觉Q-模糊理想，则A∩B是X的直觉Q-模糊理想.

证明因为A=(αA,βA)和B=(αB,βB)是X的直觉Q-模糊理想,所以∀x,y,z∈X，q∈Q,有

αA(x*y,q)≥αA(y,q),αA((x*(y*z))*z,q)≥αA(x,q)∧αA(y,q)，

βA(x*y,q)≤βA(y,q),βA((x*(y*z))*z,q)≤βA(x,q)∨βA(y,q)，

αB(x*y,q)≥αB(y,q),αB((x*(y*z))*z,q)≥αB(x,q)∧αB(y,q)，

βB(x*y,q)≤βB(y,q),βB((x*(y*z))*z,q)≤βB(x,q)∨βB(y,q).

于是，有

αA∩B(x*y,q)=αA(x*y,q)∧αB(x*y,q)≥αA(y,q)∧αB(y,q)=αA∩B(y,q)，

βA∩B(x*y,q)=βA(x*y,q)∨βB(x*y,q)≤βA(y,q)∨βB(y,q)=βA∩B(y,q).

又∀x,y,z∈X,A和B是X的直觉Q-模糊理想, 所以，有

αA∩B((x*(y*z))*z,q)=αA((x*(y*z))*z,q)∧αB((x*(y*z))*z,q)≥

(αA(x,q)∧αA(y,q))∧(αB(x,q)∧αB(y,q))=

(αA(x,q)∧αB(x,q))∧(αA(y,q)∧αB(y,q))=αA∩B(x,q)∧αA∩B(y,q)，

βA∩B((x*(y*z))*z,q)=βA((x*(y*z))*z,q)∨βB((x*(y*z))*z,q)≤

(βA(x,q)∨βA(y,q))∨(βB(x,q)∨βB(y,q))=

(βA(x,q)∨βB(x,q))∨(βA(y,q)∨βB(y,q))=βA∩B(x,q)∨βA∩B(y,q).

综上可得A∩B是X上的直觉Q-模糊理想.