一类带p(x)-双调和算子的Kirchhoff型问题的多解性

缪 清

(云南民族大学 数学与计算机科学学院，云南 昆明 650500)

研究

(1)

变指数算子的微分方程可以描述“逐点异性”的物理现象，它来源于非线性弹性力学[1].问题(1)带有非局部项，此类问题常被称为Kirchhoff型问题.近年来，关于Kirchhoff型问题的研究得到了很多结果[2-6].文献[3]利用环绕定理,证明一类带Dirichlet边值条件的p-Kirchhoff型问题解的存在性.文献[4]研究一类p(x)-Kirchhoff型问题解的存在性. 然而，关于带p(x)-Kirchhoff型双调和问题的结果相对较少.文献[7]利用Ekeland变分原理，证明问题(1)中当f(x,u)=λ|u|q(x)-2u时解的存在性与多解性.

当问题(1)中f(x,u)=λa(x)|u|γ(x)-2u时，文献[8]证明问题解的存在性.文献[9]在非线性项满足 Ambrosetti-Rabinowitz(AR)条件时得到问题(1)的多解性，且AR条件可以得到f(x,u)关于变量u在无穷远处是超线性的.论文主要研究非线性项不满足AR条件时问题(1)的多解性.

1 预备知识及引理

令

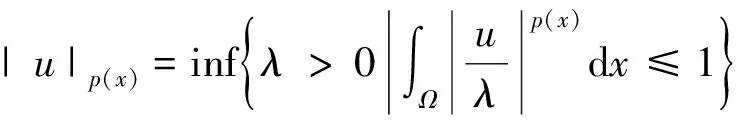
定义空间Wm,p(x)(Ω),有

Wm,p(x)(Ω)={u∈Lp(x)(Ω)|Dαu∈Lp(x)(Ω),|α|≤m},

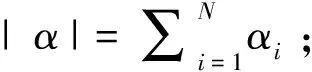
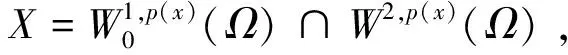
则范数‖·‖,|Δ·|p(x),‖·‖2,p(x)在X中是等价的[11],X是可分的自反Banach空间， 则存在{ej}⊂X，使得

则X=Yk⊕Zk，给定k∈N,Yk是X的k维子空间.

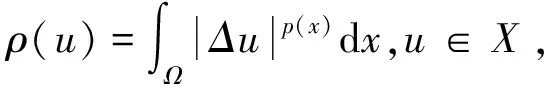
(a) 若‖u‖≥1,有

‖u‖p-≤ρ(u)≤‖u‖p+.

(b) 若‖u‖≤1,有

‖u‖p+≤ρ(u)≤‖u‖p-.

(c) ‖u‖→0⟺ρ(u)→0.

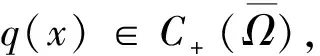
定义函数

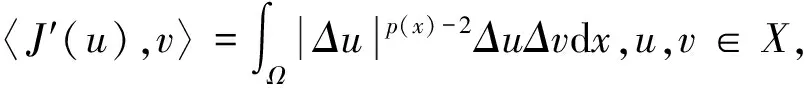
引理3[13](i)J′ 是连续的有界严格单调算子；

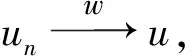
(iii)J′是同胚的.

引理4[14](喷泉定理) 泛函φ∈C1(X,R),φ(0)=0,φ(-u)=φ(u),且满足

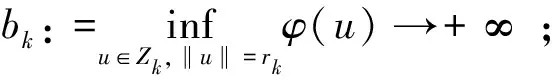
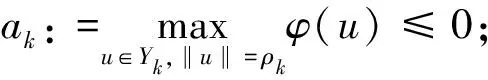
(iii) 若函数φ满足：对任何点列{un}⊂X，当{φ(un)}有界，(1+‖un‖)‖φ′(un)‖→0 时，{un}有收敛子列，即称φ满足(C)条件.

则泛函有一列趋于+∞的临界值.

2 主要结果

令ci为正常数，定义泛函Φ为

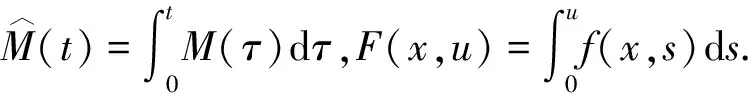
则u是问题(1)的弱解等价于u是泛函Φ的临界点.

函数M(t),f(x,t)满足以下条件:

(M0) 存在正常数m0,满足M(t)≥m0(∀t≥0);

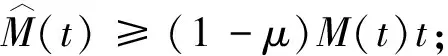
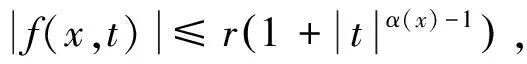
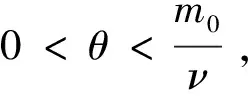
(F2)F(x,0)=0,F(x,-t)=F(x,t)对所有的x∈Ω,t∈R成立;

引理5假设条件(M0),(M1),(F0),(F1)满足，则Φ(u)满足(C)条件.

证明设{un}⊂X为Φ的(C)序列，首先证明序列{un}在X中有界.假设当n→∞时，‖un‖→+∞，由条件(F1),存在K>1,使得

(2)

令Ωn={x∈Ω||u|>K}，由(2)式，存在σ>0,有

不等式两边同时除以‖un‖p-，当n→∞时，矛盾，因此，{un}在X中有界. 由于X是自反空间，则存在u∈X,使得{un}在X中弱收敛于u、在Lα(x)中强收敛于u.由Holder不等式和条件(F0),当n→∞时，有

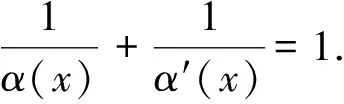
当n→∞时，有Φ′(un)→0,可知

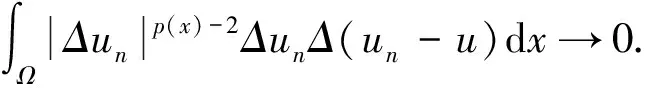
定理假设条件(M0),(M1),(F0)～(F3)成立，则问题(1)有一列解{un}满足：当n→∞时，有Φ(un)→+∞.

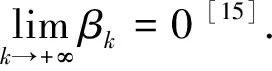
对于u∈Zk,‖u‖=rk>1，由条件 (M1),(F0)可知

因此，有

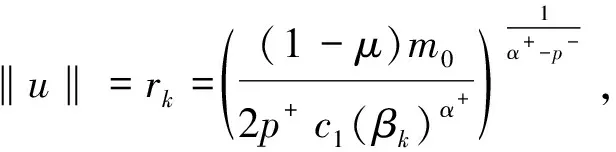
由条件(F3)，对任意的τ>0,∃c3>0，使得

当u∈Yk,‖u‖=ρk>rk>1时，有

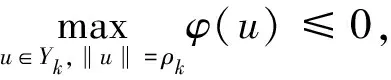
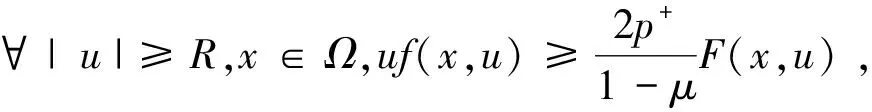
则条件(F1)不满足(AR)条件.