数理金融学研究方法存在的错误及纠正方法探析
2020-01-14高宏
高宏


摘要: 金融资产价格随时间演变的过程为非平稳随机过程,本文指出了数理金融学将平稳随机过程随机变量研究方法用于研究非平稳资产价格过程样本函数的方法存在错误。分析了数理金融学随机变量研究方法的错误现象及历史原因,并使用样本函数研究方法重建了描述资产价格随时间演变过程的随机游走数学模型,推导出了资产价格的自相关函数和功率谱密度,给出了预测股票市场指数长期趋势和波动范围的原理及方法。
关键词: 资产价格模型 随机游走 维纳过程 非平稳随机过程
一、引言
任何一门学科的现代化和精确化进程,都必然导致以数学语言和数学工具来研究该学科研究对象的运动状态、内在联系及运动规律。数理金融学就是运用随机过程理论和方法,来建立描述资产价格波动现象的数学模型,并发现其内在运动规律和特征,以解决不确定环境下金融资产定价、最优配置和风险管理等问题。早在1900年,数理金融学的奠基人、法国数学家Bachelier就首先使用概率方法对股票价格现象进行定量研究,建立了描述股票价格波动现象的算术布朗运动模型。从现代随机过程的角度看,Bachelier采用随机变量方法来研究非平稳随机过程样本函数,无意中使数理金融学的研究对象发生了错位,势必会得出一系列与事实不符的错误结论。令人不可思议的是,数理金融学一直沿用Bachelier的错误研究方法研究金融市场的数量关系及其变化规律,导致广泛应用时给金融市场带来巨大的灾难,畅销书《黑天鹅》作者Taleb在《金融时报》上发表专栏文章,将数理金融学斥之为“破坏市场的伪科学”。
二、非平稳随机过程的特点及研究方法
随机过程X(ω,t)是定义在Ω×T上的二元函数。对于固定的t∈T,X(ω,t)是定义在状态空间Ω上的函数,称为随机变量,简记为大写的X(t);对于固定的ω∈Ω,X(ω,t)是时间的函数,称为样本函数,简记为小写的x(t)。人们观察到的股票价格随时间变化过程,只是随机过程中的一个样本函数。
对于平稳随机过程中的各态历经过程,各个样本函数都同样经历了整个随机过程在状态空间所有可能的状态,因此,任何一个样本函数所作的各种时间平均(均值、均方值),在概率意义上等于此过程随机变量在状态空间的各种统计平均(数学期望、方差)。因此在研究这类随机过程时,即可用随机变量的统计特征来描述任何一个样本函数,也可用任何一个样本函数的时间平均来代替随机变量的统计平均。
但是对于非平稳随机过程X(ω,t),其随机变量X(t)的统计平均与各个样本函数x(t)的时间平均完全不同,因此在研究非平稳随机过程X(ω,t)时,对随机变量X(t)和样本函数x(t)要采用分别研究的方法,否则会使研究对象发生错位,得出与事实完全不符的错误结论。
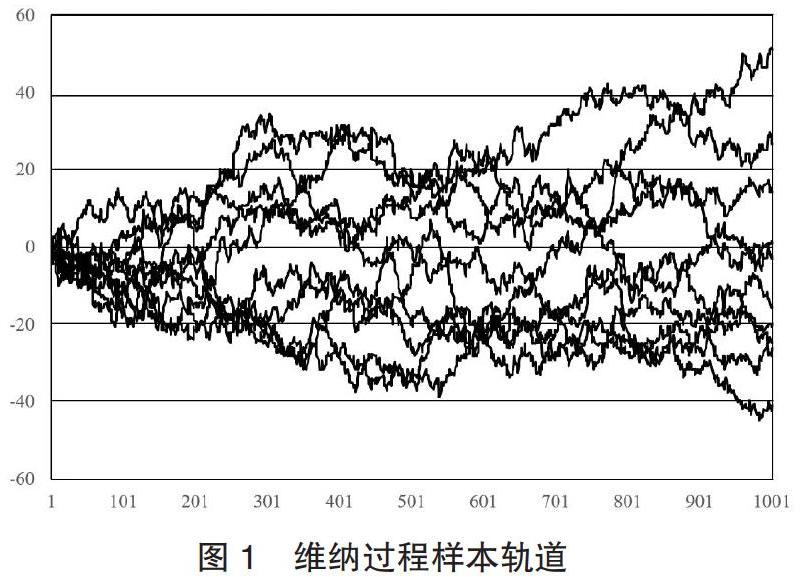
非平稳随机过程随机变量的统计特性不但是时间的函数,而且各个样本函数的时间平均也是各不相同的时间函数。例如,维纳过程随机变量W(t)的数学期望为零,方差与时间成正比,因此维纳过程是典型的非平稳随机过程。维纳过程的样本函数是均值随时间变化、均方值为常数的时间函数,图1给出了10条维纳过程样本函数的仿真曲线。从图中可以看出,维纳过程所有样本轨道的均方值(方差)都为固定的常数,但样本轨道在状态空间呈发散状态,样本轨道的发散程度可用维纳过程随机变量W(t)的方差进行度量。
三、随机变量研究方法的错误
证券交易所给出的股票价格s是时间t的函数,它只是股票价格随机过程S(t)中的一个样本函数s(t)。金融领域大量的实证研究结果表明,股票价格的对数收益率为零均值不相关白噪声序列,设y(t)=ln s(t),因此有
式中σ为股票价格对数收益率的标准差,ε(t)为均方差为1的白噪声过程样本函数,这里不要求ε(t)服从正态分布,只需ε(t)的均值为零,在不同时刻的取值互不相关即可。
式(1)表明:股票对数价格y(t)的一阶差分Δy(t)为零均值不相关白噪声样本函数ε(t),这是众多学者通过对股票价格波动现象长期观察和实证研究得到的规律性认识,它是构建数理金融学理论的基础或公理。
1958年,Osborne通过对美国纽约证券交易所股票价格数据的实证分析发现,股票价格的对数收益率服从均值为零的正态分布,与维纳过程增量的统计特征完全相同,于是建立了下面的股票价格随机变量模型
式中的维纳过程W(t)为标准布朗运动,ΔW(t)服从(0,1)正态分布。
式(2)可改写随机游走形式的股票价格模型
式中Y(t)服从参数为(0,tσ2)正态分布。
1965年,Fama使用式(3)的随机变量模型来描述实际股票价格现象,并将随机变量模型的统计特性用于股票价格样本函数,建立了著名的EMH(Efficient Market Hypothesis)有效市场假说,得出了股票市场未来的价格变化与当前和过去的历史价格无关,股票价格波动中不存在趋势和规律,股票市场不可预测等一系列结论。有效市场假说直接推翻了技术分析中“价格沿趋势运动”的基本假设,认为投资者完全无法根据股票市场历史价格来预测其未来的走势,最终得出了技术分析无效的结论。
若将Y(t)数学期望为零的统计特性用于样本函数y(t),则无法描述和解释实际股票价格y(t)中存在长期线性趋势这一现象。Samuelson为了解决式(2)与事实不符的问题,不是从式(2)的随机变量假设去寻找原因,而是画蛇添足地给式(2)增加了线性漂移项,建立了带漂移的几何布朗运动模型
式中μ为股票期望收益率,也称股票价格漂移率。
1973年,Black和Scholes基于式(4)推导出了著名的BS期权定价公式。由于从理论上解决了金融衍生产品的定价问题,BS期權定价公式直接导致了“第二次华尔街数学革命”,对各种金融创新工具和金融创新产品的面世起到了重大推动作用,使华尔街金融市场获得了空前规模的发展。让人意外的是,BS期权定价公式的广泛应用,竟成为直接导致1987、1997和2007年三次重大金融危机的主要原因之一。
事实上,Osborne早在1958年就得出了股票对数价格的方差与时间成正比的结论,证明股票价格过程为非平稳随机过程。但是Osborne本人,以及后来的Fama、Samuelson、Black、Scholes和Merton等数理金融学家,依旧使用Bachelier在1900年使用的随机变量研究方法来研究非平稳的股票价格样本函数,从而将数理金融学理论建立在错误的随机变量假设基础之上。
四、样本函数研究方法
股票价格随时间演变的过程是非平稳随机过程中的一个样本函数,因此我们只能采用样本函数分析方法,来建立股票价格现象的样本函数模型,研究其自相关函数、功率谱密度、长期线性趋势及波动范围等时域和频域特性。
(一)时间函数模型
由式(1),直接可得积分形式的股票价格随机游走模型
式中积分上限随时间变化,表明随机游走模型为非线性时变模型。
(二)自相关函数
由式(5),可推导出y(t)的自相关函数
式中为时间间隔。Ry()在很宽的范围内具有非零值,表明y(t)中存在可以识别和利用的规律,y(t)具有可预测性。
(三)功率谱密度
y(t)平均功率有限,Ry()绝对可积,根据维纳-辛钦定理,y(t)的功率谱密度函数Sy(ω)是Ry()的傅立叶变换,有
式中,Sinc(ωt)为辛格函数。Sy(ω)为时变功率谱,Sy(ω)与ω的平方成反比,因此y(t)是能量集中在低频段的红噪声。
(四)长期趋势和波动范围的预测原理及方法
式(1)的模型不仅能够描述、解释过去和现在的资产价格现象,更重要的是能够预测股票市场指数未来的发展趋势和变化范围。将式(1)变化为
式中为ε(t)在[0,t]区间上的算术平均值,其物理意义表示白噪声信号在有限区间被截断后因“频谱泄露”效应而产生的直流分量。
也是一随机过程样本函数,由概率论大数定律可知,随着t的增加,的数学期望E[]会趋于真值(常数),因此,y(t)中存在一条σE[]t的长期线性趋势线。
设的标准差为σε,利用切比雪夫不等式,可以确定在E[]±σε范围内出现的概率为99.73%,因此,y(t)也会在相应的范围内进行波动,从而可以得出如下的推论:
推论:股票对数价格在线性通道内围绕长期线性趋势线波动运行。
在实际预测股票市场指数的未来长期趋势和波动范围时,使用技术分析中的轨道线作图法就能确定长期线性通道。例如,在对数坐标下,将上证指数历史数据的最高点连成一条直线,可得线性通道的上轨道线;将上证指数历史数据的最低点连成一条直线,可得線性通道的下轨道线,上证指数未来20年、50年,甚至100年都将以99%以上的概率在上、下轨道线构成的线性通道内运行。如果未来上证指数接近上轨道线运行,表示市场已经到达牛市的顶部;如果上证指数在下轨道线附近运行,则表明市场处于熊市的底部。
五、结论
本文指出了数理金融学将随机变量研究方法用于研究非平稳随机过程样本函数的方法错误。并用样本函数研究方法重建了股票价格数学模型,推导出了可揭示股票价格运动规律及特征的自相关函数和功率谱密度,给出了预测股票市场指数未来长期趋势和波动范围的原理及方法,可为证券投资活动的价格分析、价格预测及风险管理提供有效的数学模型及分析工具。
作者单位:清华大学
